Execution Strategies in the Institutional Spot FX Market

Execution Strategies in the Institutional Spot FX Market: Simulations and Analysis Alec Schmidt Business Development & Research ICAP Electronic Broking Parsippany NJ USA Email: Alec. Schmidt@us. icap. com April 2011

2 Agenda • Specifics of the EBS market relevant for this presentation. • Taker’s dilemma: a maker order (i. e. joining current best price) or a taker (buy/sell) order. • Optimal execution of large orders: Implementation shortfall.

3 1. 1 EBS market: Orders EBS is a limit order market. Two types of orders available: • Quotes (bid/offer orders) stay in the order book until they are filled or cancelled. A quote can be a Maker or a Taker order (if two quotes match, the one that comes in the market later is the Taker). • Hits (buy/sell orders) are submitted at current best price and are automatically cancelled if there are no matching quotes in the market at the time of their arrival. Hit can only be a Taker.

4 1. 2 EBS market: Credit Trading can only occur between counterparties that have bilateral credit. EBS customers establish credit with each other, and can change it at any time. As a result: • The market best price may not be available to a Taker if he does not have bilateral credit with the Maker. • A Maker order may get executed before it reaches the top of the order book

5 1. 3 EBS market: Distributed architecture • Order matching in three regions: LN, NY, TY. • Consolidated regional order books are identical. • The order relative positions in different regional order books may be not identical. • Regional matching.

6 2. 1 Taker’s dilemma: Two strategies Two order submission strategies: • Taker strategy (e. g. buy order at the best offer price). It has a high certainty of being dealt quickly, but incurs a loss equal to the bid/offer spread. • Maker strategy (e. g. bid order at the best bid price). It has a lower certainty of being dealt quickly (if at all), but does not incur immediate loss.

7 2. 2 Taker’s dilemma: Defining the maker strategy • Trader submits a Maker order at market price (e. g. a long order at the best bid price). • If price worsens before execution, the order is cancelled and then resubmitted at the new market price. Will this strategy yield a lower loss than the Taker strategy? (Loss is defined as the difference between the actual execution price and the initial order price).

8 2. 3 Taker’s dilemma: Simulation of a single run Input: • • Best price - observable Volume at best price - observable Deal depletion rate – from simulations Total depletion rate (deals + cancellations) – from simulations Output: • • Expected loss Expected execution time

9 2. 4 Taker’s dilemma: Handling the order volumes on top of the book The real order book volumes Ve are used along with simulated volumes Vs using the depletion rate R

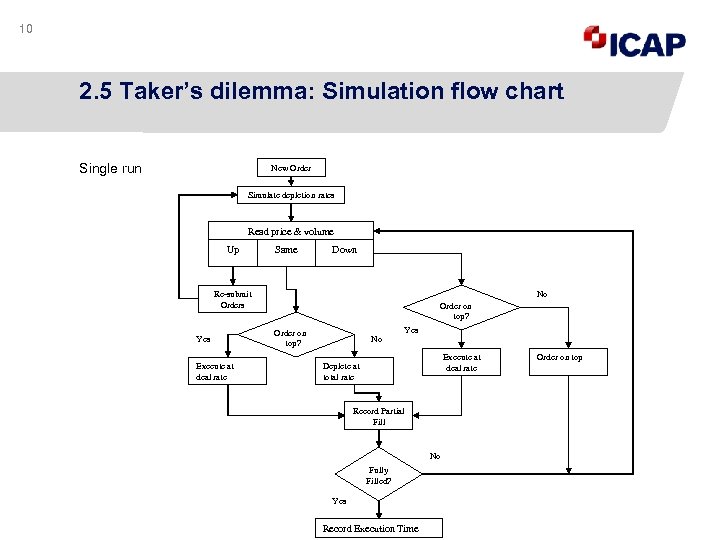10 2. 5 Taker’s dilemma: Simulation flow chart Single run New Order Simulate depletion rates Read price & volume Up Same Down No Re-submit Orders Yes Execute at deal rate Order on top? No Yes Execute at deal rate Deplete at total rate Record Partial Fill No Fully Filled? Yes Record Execution Time Order on top

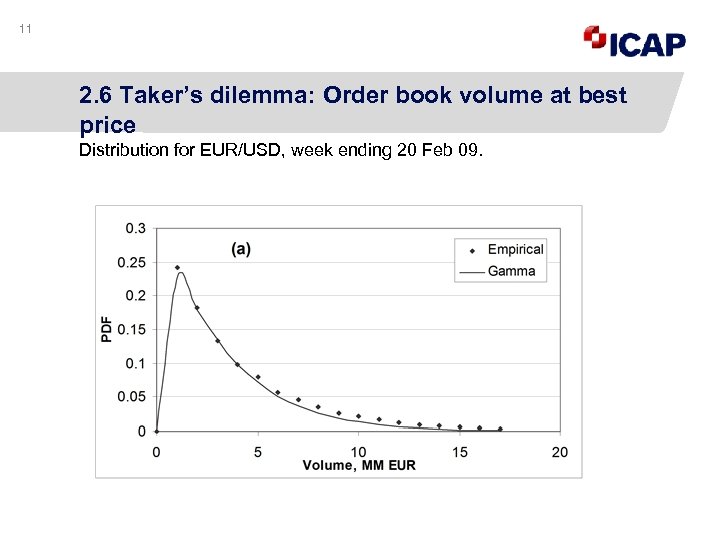11 2. 6 Taker’s dilemma: Order book volume at best price Distribution for EUR/USD, week ending 20 Feb 09.

12 2. 7 Taker’s dilemma: Gamma distribution The Gamma distribution is defined with two parameters: alpha and beta:

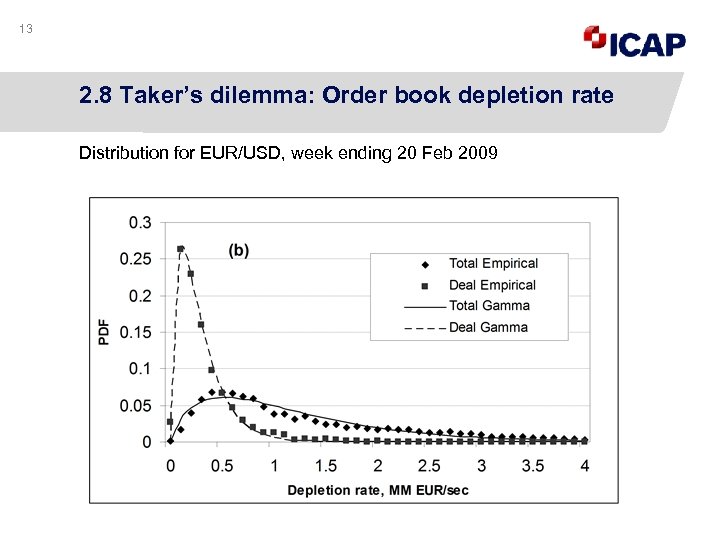13 2. 8 Taker’s dilemma: Order book depletion rate Distribution for EUR/USD, week ending 20 Feb 2009

14 2. 9 Taker’s dilemma: Multiple runs Sequential Runs – not good… Autocorrelations in EUR/USD:

15 2. 10 Taker’s dilemma: Resampling • Sequential Run (SR) • Bootstrap (BSn) • MCMCn • Random entry (RE)

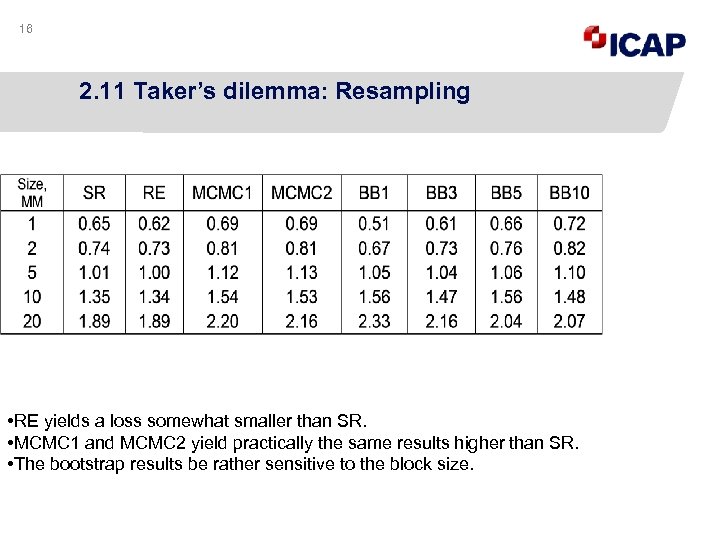16 2. 11 Taker’s dilemma: Resampling • RE yields a loss somewhat smaller than SR. • MCMC 1 and MCMC 2 yield practically the same results higher than SR. • The bootstrap results be rather sensitive to the block size.

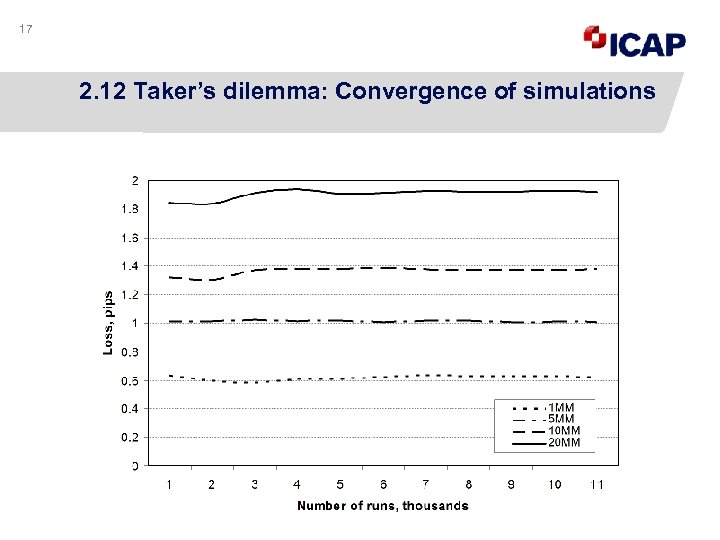17 2. 12 Taker’s dilemma: Convergence of simulations

18 2. 13 Simulations of Maker Strategy: Expected Loss (pips)

19 2. 14 Simulations of Maker Strategy: Expected Execution Time (sec)

20 3. 1 Optimal execution of large orders: Lessons from equity markets Solution: slicing large orders into small pieces and submitting them as market orders. Implementation shortfall strategies: The smaller the pieces - the lower market impact (E), but the longer the execution time, and hence - the higher the volatility risk (V). Amgren & Chriss (2000): min [E + λV]

21 3. 2 Optimal execution of large orders: Problems in FX • Institutional FX is essentially a limit-order market. Hence transactional volume alone cannot determine market impact (MI). • Realized MI is not equal to expected MI. • MI cannot be reduced to a sum of the permanent and temporary components. MI has a power-law decay. • Child orders are executed not at a single price but within a range.

22 3. 3 Optimal execution of large orders: The model The definitions: Selling X millions within the time T; N periods with length τ = T/N; tk = k*τ, k = 0, 1, …, N. The list n = {n 0, …, n. N}, ni is the number millions sold within ti-1 < t ≤ ti. Another list x = {x 0, …, x. N}, xk =X x 0 = X; x. N = n 0 = 0. MI: F(ni, tk - ti), k > i. Initial market impact (IMI): sk = -F(nk, 0) =

23 3. 4 Optimal execution of large orders: The model (2) E(n) = - VWAP increment (VWAPI) ck(nk) = Sk-1 - SVWAPk V(n) = σ2τ • Assumptions: ck(nk) = αnk (1) • sk(nk) = βnk (2) • F(nk, t) = γsk(nk)/(t-tk)m, t > tk (3)

24 3. 5 Optimal execution of large orders: The solution Analytical solution if only (k-1)th term is accounted in ni = κ 02 = λσ2/ (α + βγτ-m) 2(cosh(κτ) – 1) = κ 02τ2

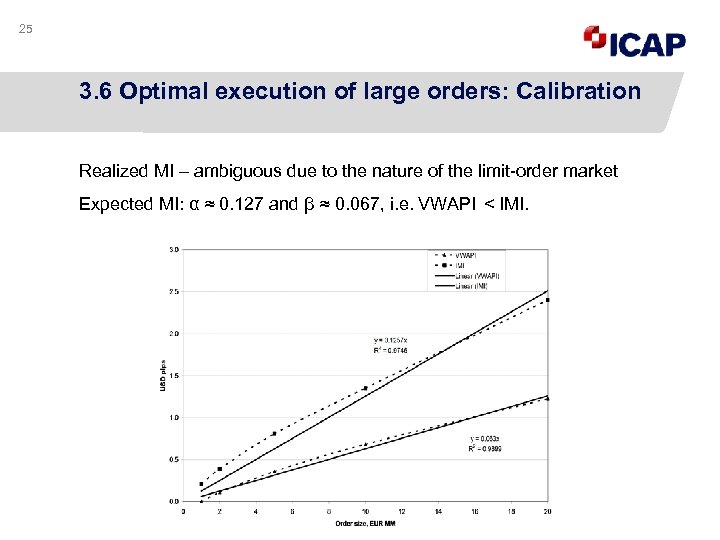25 3. 6 Optimal execution of large orders: Calibration Realized MI – ambiguous due to the nature of the limit-order market Expected MI: α ≈ 0. 127 and β ≈ 0. 067, i. e. VWAPI < IMI.

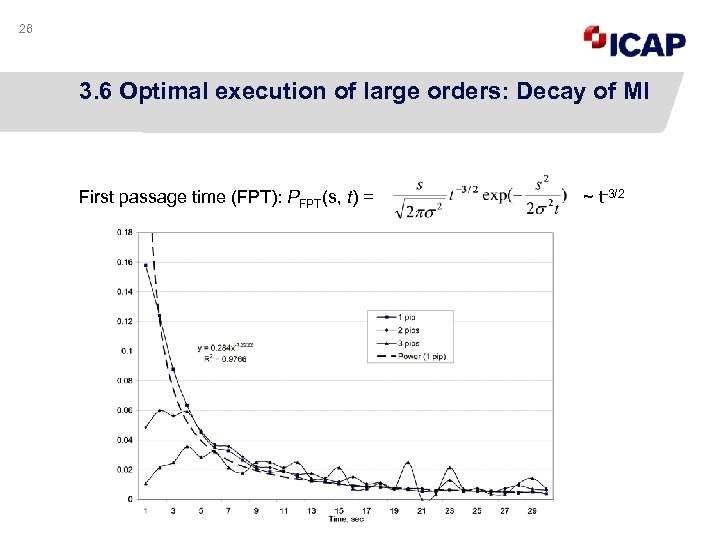26 3. 6 Optimal execution of large orders: Decay of MI First passage time (FPT): PFPT(s, t) = ~ t-3/2

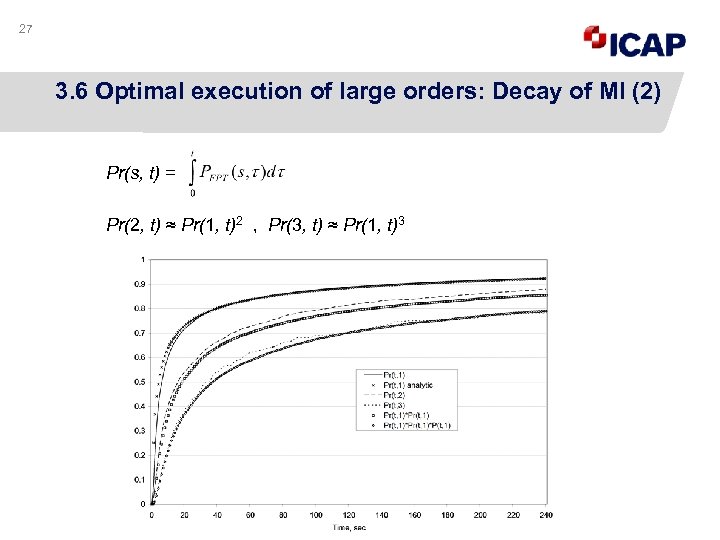27 3. 6 Optimal execution of large orders: Decay of MI (2) Pr(s, t) = Pr(2, t) ≈ Pr(1, t)2 , Pr(3, t) ≈ Pr(1, t)3

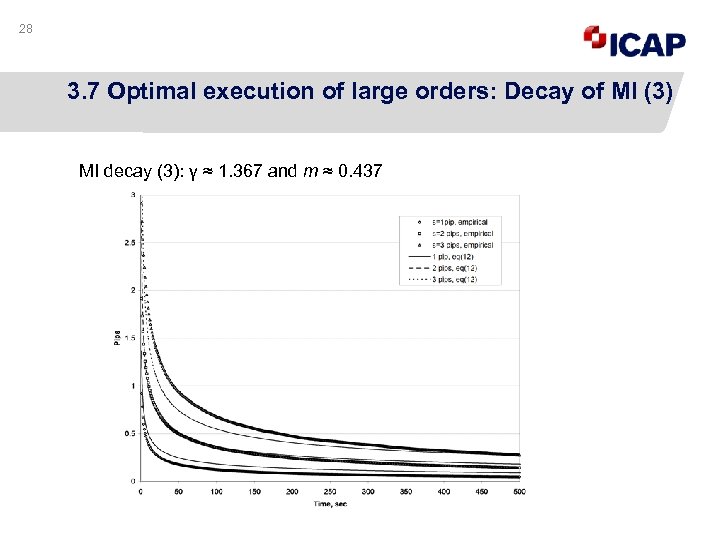28 3. 7 Optimal execution of large orders: Decay of MI (3) MI decay (3): γ ≈ 1. 367 and m ≈ 0. 437

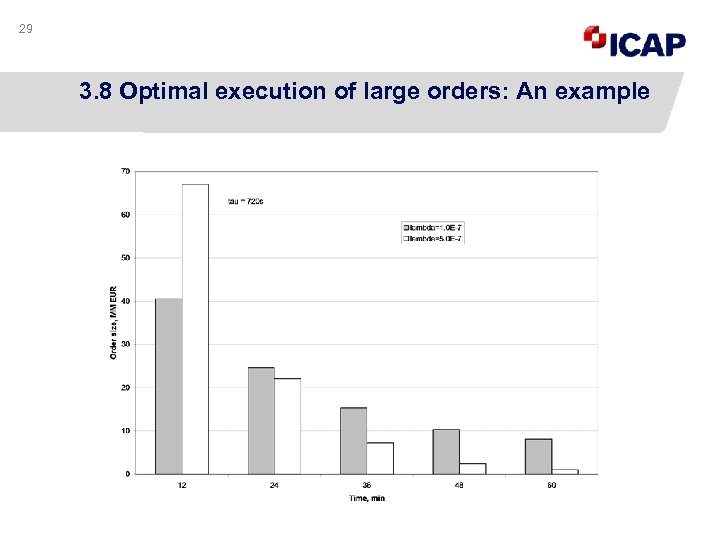29 3. 8 Optimal execution of large orders: An example

30 Q&A