Exchange Rates CHAPTER 13 1 Exchange Rates

Exchange Rates CHAPTER 13 1

Exchange Rates n What are they? n How does one describe their movements? 2

Exchange Rates n The nominal exchange rate is the price of one currency in terms of another. n The spot rate applies to trades “on the spot”. 3

4

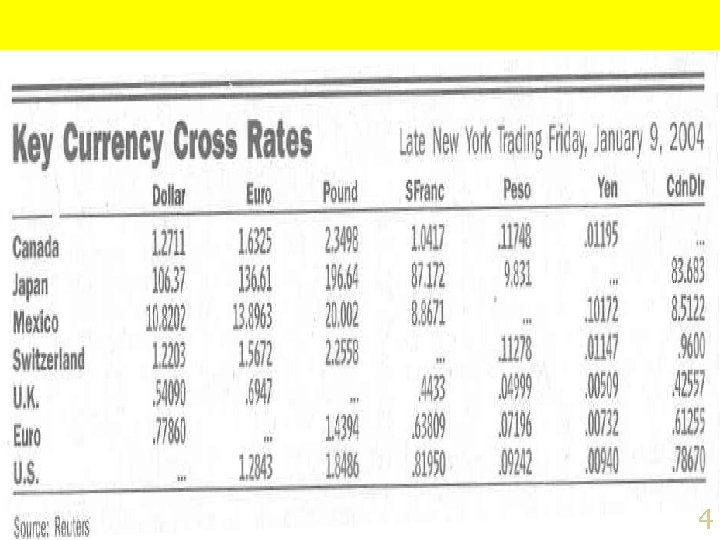
Exchange Rate Quotes Currency Trading WSJ Section C, January 11, 2004 US $ equivalent Currency per US $ (E$/¥) (E¥/$) Japan . 00940$ 106. 37 ¥ n E = EHC/FC is the home currency value of the foreign currency 5

6

7

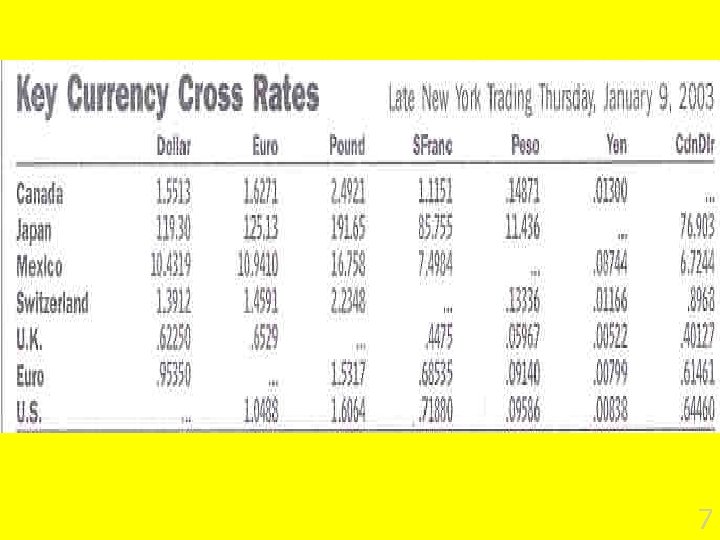
Between Jan 2003 and Jan 2004 n Which currency appreciated? n Did E rise? 8

Who Participates in this Market? n Banks and near banks n Corporations n Central Banks 9

Other Characteristics n Volume n Vehicle Currencies n Spot and Forward Markets 10

What Are the Effects of Changes in E? n Gains and losses for international asset holders n Changes in price competitiveness in international goods markets 11

Exchange Rates & Imports n US import (Japanese car) sells for 2 mill. ¥ n As the ¥ appreciates & the $ depreciates, the price of US imports E$/¥ E¥/$ Price of US Import ($) . 008. 010. 012 125 100 83 . 008(2000000) = $16000. 01(2000000) = $20000. 012(2000000) = $24000 12

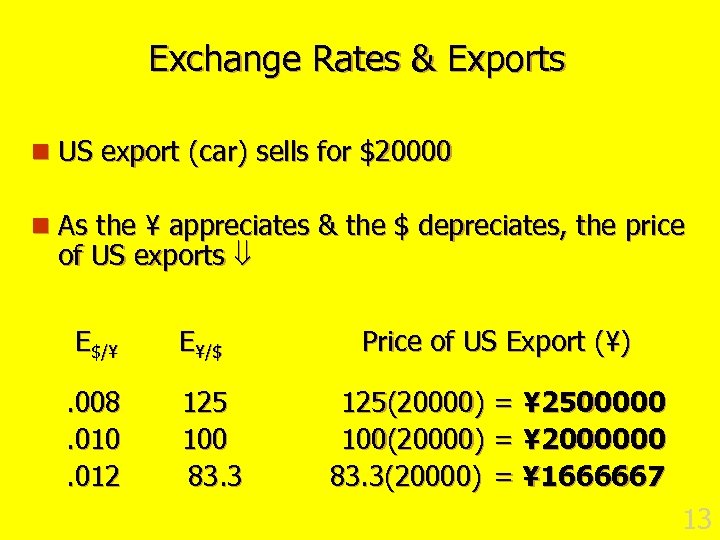Exchange Rates & Exports n US export (car) sells for $20000 n As the ¥ appreciates & the $ depreciates, the price of US exports E$/¥. 008. 010. 012 E¥/$ 125 100 83. 3 Price of US Export (¥) 125(20000) = ¥ 2500000 100(20000) = ¥ 2000000 83. 3(20000) = ¥ 1666667 13

Forward Rates Spot $ per £ 30 day forward 90 day forward 180 day forward 1. 8486 1. 8443 1. 8355 1. 8219 n A forward contract is a contract to trade in the future n Forward rates indicate market expectations for the future. 14

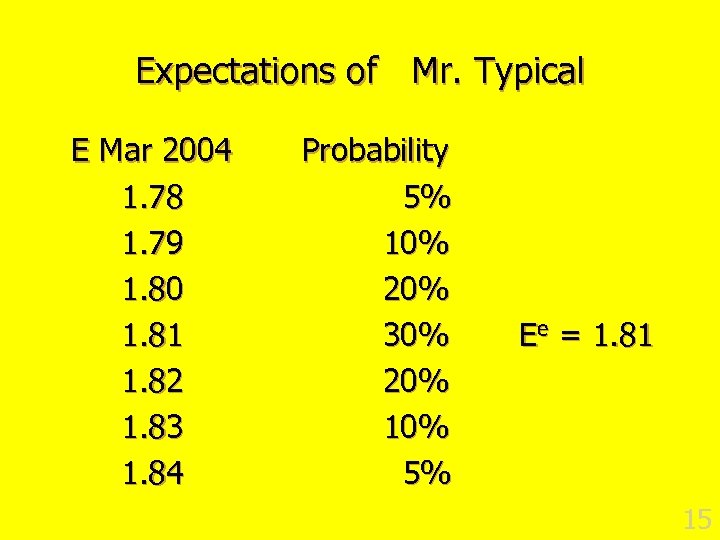Expectations of Mr. Typical E Mar 2004 1. 78 1. 79 1. 80 1. 81 1. 82 1. 83 1. 84 Probability 5% 10% 20% 30% 20% 10% 5% Ee = 1. 81 15

Expectations and Forward Rates n Current (six month) forward rate on the £: n F$/£ =1. 82 n Mr Typical decides to speculate n Goes “short” in the forward market for pounds 16

Expectations and Forward Rates Mr. Typical’s plan: n Agree to sell $100000 worth of pounds (£ 54945= 100000/1. 82) in 6 months n Next March buy £ 54945 on the spot market for $99450 (=54945 x 1. 81) and sell it for $100000 as agreed. 17

Expectations and Forward Rates n If “the market” agrees with Mr. Typical’s expectation (guess) and acts on it: n Lots of sellers of pounds (buyers of dollars) in the forward market and few buyers. n F$/£ falls until it equals 1. 81 ( =Ee) 18

Is this result based on the notion that everyone thinks E will fall to 1. 81 ? No 19

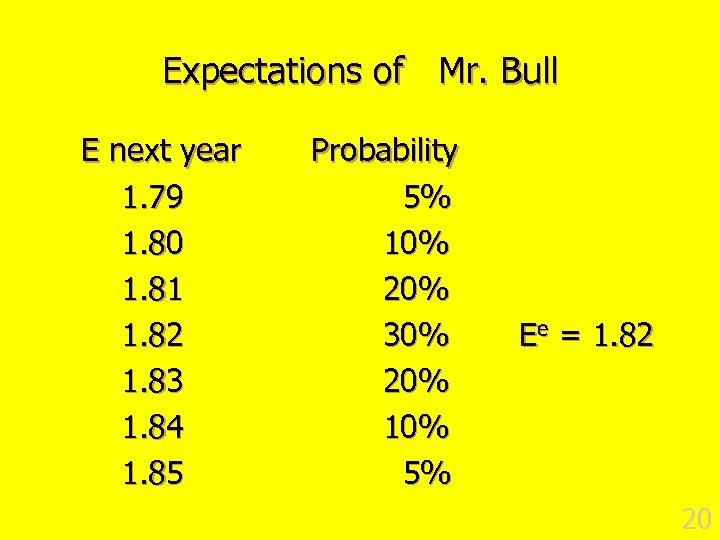Expectations of Mr. Bull E next year 1. 79 1. 80 1. 81 1. 82 1. 83 1. 84 1. 85 Probability 5% 10% 20% 30% 20% 10% 5% Ee = 1. 82 20

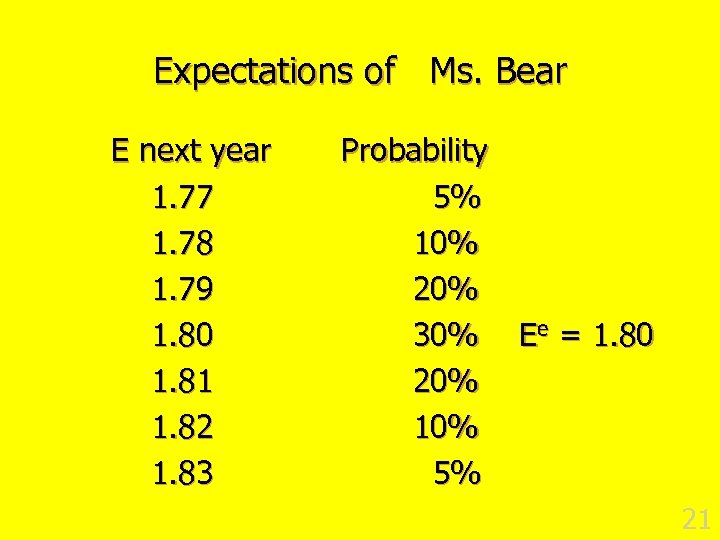Expectations of Ms. Bear E next year 1. 77 1. 78 1. 79 1. 80 1. 81 1. 82 1. 83 Probability 5% 10% 20% 30% Ee = 1. 80 20% 10% 5% 21

Expectations and the Forward Rate n Suppose F$/£ falls until 1. 81 = Ee n Mr. Bull goes “long” in the pound (committed to buy at 1. 81; hopes to sell at 1. 82) n Ms. Bear sells the pound “short” (committed to sell at 1. 81; hopes to buy at 1. 80) n Mr. Typical stays out of the market 22

Expectations and the Forward Rate n Ee =1. 81 means as much money thinks the spot rate will be above 1. 81 as thinks that it will be below 1. 81 in July n If F$/£ > 1. 81 speculators will flood “short” side of the market until F$/£ = 1. 81 n If F$/£ < 1. 81 speculators will flood “long” side of the market until F$/£ = 1. 81 23

Who Participates in Forward Markets? n Speculators n Hedgers 24

Hedging n Forward contracts can be used to protect against (hedge) exchange risk Value of 1 Million Pounds in 30 days Value of £ Value of $ $ 1. 60 $ 1. 80 $ 2. 00 £ 0. 63 £ 0. 56 £ 0. 50 $ Receipts $ 1600000 $ 1800000 $ 2000000 25

Other Contracts n An option gives you the right, but not the obligation, to trade currencies in the future n A futures contract requires the payment of $ now, in order to receive a specified amount of £’s in the future. 26

What Makes (spot) Exchange Rates Fluctuate? 27

Exchange Rate Determination n What makes E rise and fall? n Supply and Demand (of course) n What makes Supply and Demand fluctuate? n Most exchanges of currency are used to finance the purchase of foreign assets not foreign goods 28

Interest Parity Why Should Interest Rates be Different in Different Countries? 29

Equilibrium Exchange Rate n Asset market approach to E – E is determined by financial factors. n International trades of assets are far larger than international trades of goods n The value of the foreign currency (E) depends on interest rates here & abroad, RHC, & RFC, and expectations of the future 30

Demand Foreign Currency Assets n Factors influencing this decision u Interest rates at home & abroad, RHC & RFC u Exchange rate now, E u Expected exchange rate in the future, Ee. Because the (expected) return on foreign bonds is [(1 + RFC)Ee/E] - 1 RFC + (Ee - E)/E The (known) return on domestic bonds is RHC 31

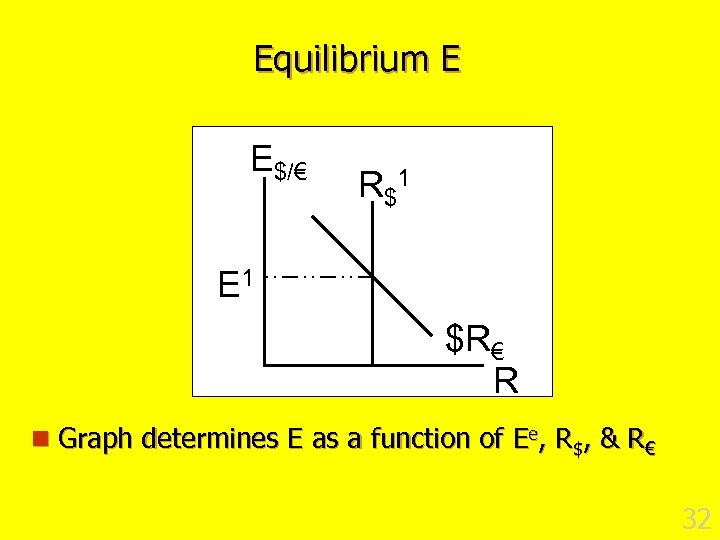Equilibrium E E$/€ R $1 E 1 $R€ R n Graph determines E as a function of Ee, R$, & R€ 32

Equilibrium E R$ = 7% R€ = 5% E$/€ = 1. 00 n Should an American investor put her funds in German assets? n Depends on what she expects to happen to E by the time she repatriates her funds 33

Equilibrium E • Suppose she expects the euro to rise to 1. 08 by next year (8% appreciation) Ee$/€ = 1. 08 • Expected return from investing abroad is [(1 + R€)Ee/E] - 1 = 13. 4% R€ + (Ee - E)/E = 13% 34

Interest Parity • Foreign assets look like a good deal (13% is better than 7%) • Of course the euro might not go up that much and the domestic return is certain • Go for it! 35

Equilibrium E • If she takes the plunge, what about everyone else? • They will too if they share her opinion that the dollar will fall by 8% 36

Equilibrium E • If lots of American do this they will be selling dollars (buying euros) on the spot market foreign exchange • Lots of sellers put downward pressure on the $ (upward pressure on the euro) • E will rise, but how far? 37

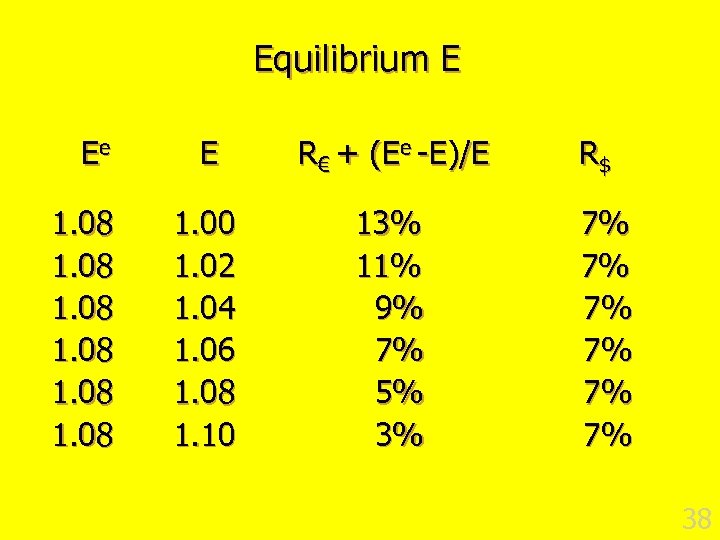Equilibrium E Ee 1. 08 E R€ + (Ee -E)/E 1. 00 1. 02 1. 04 1. 06 1. 08 1. 10 13% 11% 9% 7% 5% 3% R$ 7% 7% 7% 38

Equilibrium E E$/€ R $1 E 1 $R€ R n Graph determines E as a function of Ee, R$, & R€ 39

Equilibrium E n R$ is the US interest rate, vertical because the R$ is independent of E. n $R€ is the $ return on German bonds, R€ + (Ee - E)/E n $R€ depends negatively on E. u As current value of the € (E) , the future expected appreciation of € , & the $R€ . 40

Equilibrium E n The equilibrium condition is called interest parity, and requires the equality of expected $ returns. R$ = $R€ = R€ + (Ee - E)/E n What if R$ < $R€ = R€ + (Ee - E)/E ? n What if R$ > $R€ = R€ + (Ee - E)/E ? 41

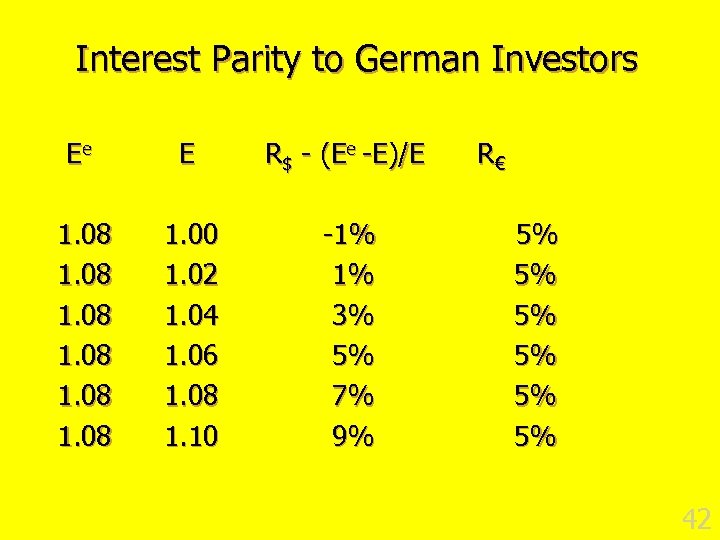Interest Parity to German Investors Ee E R$ - (Ee -E)/E 1. 08 1. 00 1. 02 1. 04 1. 06 1. 08 1. 10 -1% 1% 3% 5% 7% 9% R€ 5% 5% 5% 42

Interest Parity n E e = 1. 08 this the “typical” expectation n Maybe euro “bulls” expect 1. 10 and euro “bears” expect 1. 06 n How do they invest? 43

Interest Parity n If Mr. Bull is American, what does he do? n Best guess is a 9% return overseas n Buy foreign assets n Buy euros on the spot market (enough sellers? ) 44

Interest Parity n If Ms. Bear is American, what does she do? n Best guess is a 5% return overseas n Buy domestic assets n Stay out of the foreign exchange market 45

Interest Parity n If Mr. Typical is American, what does he do? n Best guess is a 7% return overseas n Buy domestic assets (same return, no exchange risk) n Stay out of the foreign exchange market 46

Interest Parity n If Herr Bull is German, what does he do? n Best guess is a 3% return overseas (in U. S. ) n Buy domestic (German) assets n Stay out of the foreign exchange market 47

Interest Parity n If Herr Typical is German, what does he do? n Best guess is a 5% return overseas (in U. S. ) n Buy domestic assets (same return, no exchange risk) n Stay out of the foreign exchange market 48

Interest Parity n If Frau Bear is German, what does she do? n Best guess is a 7% return overseas (in U. S. ) n Buy foreign (American) assets n Sell euros (to Mr. Bull) in spot market 49

Interest Parity n Ee = 1. 08 and “typical” investors sees approximately equal returns in foreign and domestic assets n American euro “bulls” (dollar “bears”) invest in German assets and buy €’s from German euro “bears” (dollar “bulls”) in the spot market to finance the investment 50

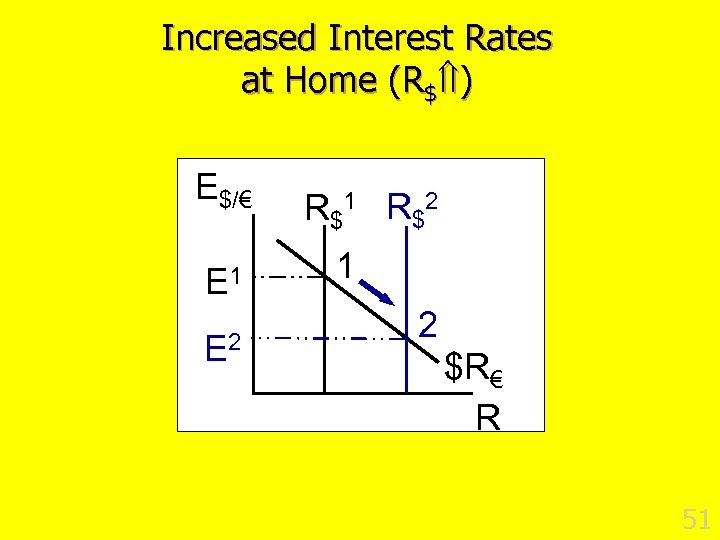Increased Interest Rates at Home (R$ ) E$/€ E 1 E 2 R $1 R $2 1 2 $R€ R 51

Increased Interest Rates at Home (R$ ) n Fed worries about inflationary pressures and pushes R$ n Bond traders move out of € & into $’s n € depreciates (E ) n $ appreciates 52

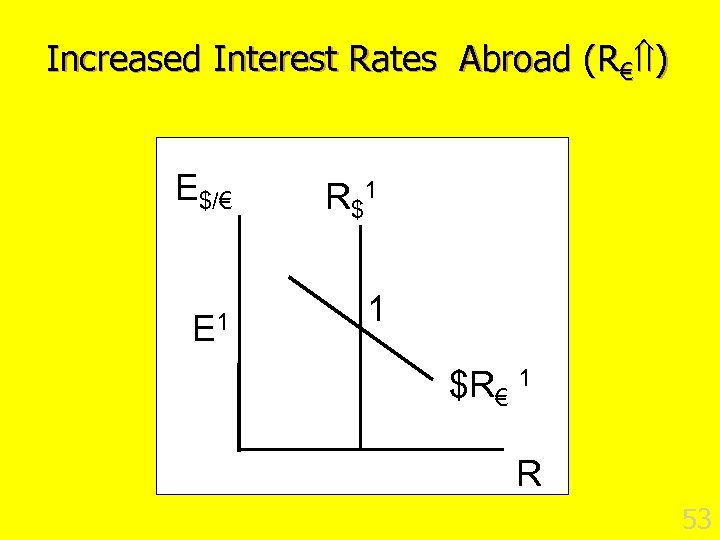Increased Interest Rates Abroad (R€ ) E$/€ E 1 R $1 1 $R€ 1 R 53

Increased Interest Rates Abroad (R€ ) n ECB becomes worried about inflation & pushes R€ . n Which way do bond traders move? n What happens to the value of the €? n What happens to the value of the $? 54

55

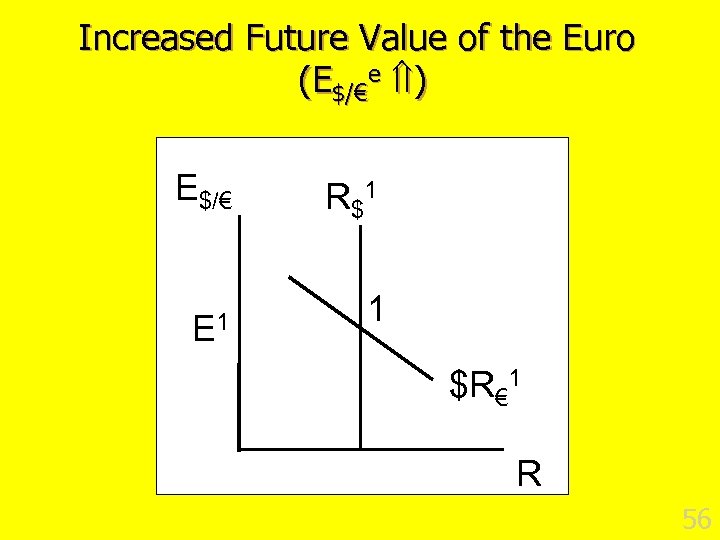Increased Future Value of the Euro (E$/€e ) E$/€ E 1 R $1 1 $R€ 1 R 56

Increased Future Value of the Euro (E$/€e ) n Future German budget deficits likely to , future R€ likely to , future E$/€e . n Which way do bond traders move? n What happens to the value of the €? n What happens to the value of the $? 57

58

Covered Interest Parity n Our earlier interest parity condition was RHC = RFC + (Ee - E)/ E n This is called uncovered interest parity, we are not “covered” against exchange risk 59

Covered Interest Parity n Covered interest parity is R$ = R€ + (F$/€ - E$/€)/ E$/€ u Forward rate replaces the expected spot rate u We are covered against exchange risk. 60

Covered Interest Parity n Suppose RHC < RFC + (F - E)/ E n How could you make a riskless profit with no money tied up? 61

Covered Interest Parity n Suppose R$ = 4% R£ = 8% E$/£ = 1. 85 F$/£ = 1. 80 n R£ + (F$/£ - E$/£)/ E$/£ = 5. 3% > R$ 62

Covered Interest Parity The PLAN: n Borrow $10000000 for 1 year at 4% n Buy £ 5410000 on the spot market at 1. 85 n Buy £ 5410000 of 1 year British bonds at 8% n Sell £ 5840000 on the forward market at 1. 80 63

Covered Interest Parity Next year: n Take £ 5840000 (principal plus interest) and fulfill the forward contract receiving $10510000 n Repay $10400000 (principal plus interest) n Buy a Porsche with the remaining $110000 64

Covered Interest Parity Since R$ < R£ + (F$/£ - E$/£)/ E$/£ Borrow at 4% and lend at 5. 3% You get income risk free with no commitment of your own funds Too good to be true? (too good to last long) 65

R$ < R£ + (F$/£ - E$/£)/E$/£ Borrowing on U. S. credit market increases » R$ tends to rise Purchases of pounds on the spot market increase » E tends to rise Sales of pounds on the forward market increase » F tends to fall Lending in the British credit market increases » R£ tends to fall 66

Covered Interest Parity n These pressures continue as long as there is a profit to be made. n Markets adjust until: R$ = R£ + (F$/£ - E$/£)/E$/£ n Covered interest parity is restored rapidly if deviations from parity appear 67

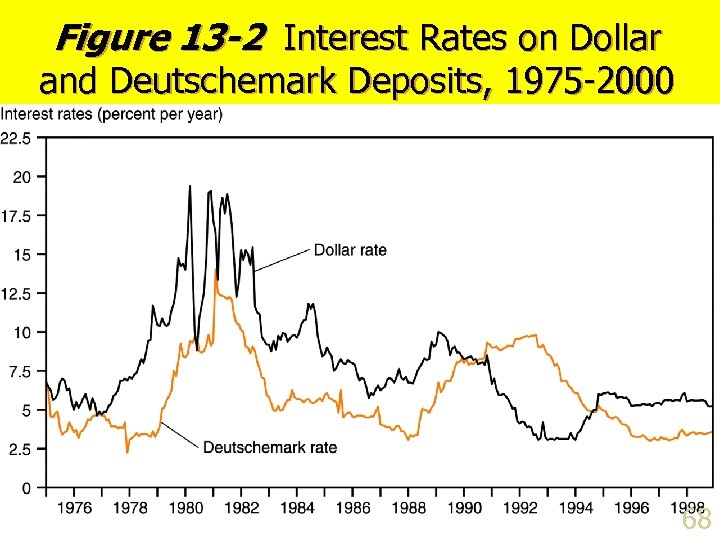Figure 13 -2 Interest Rates on Dollar and Deutschemark Deposits, 1975 -2000 68

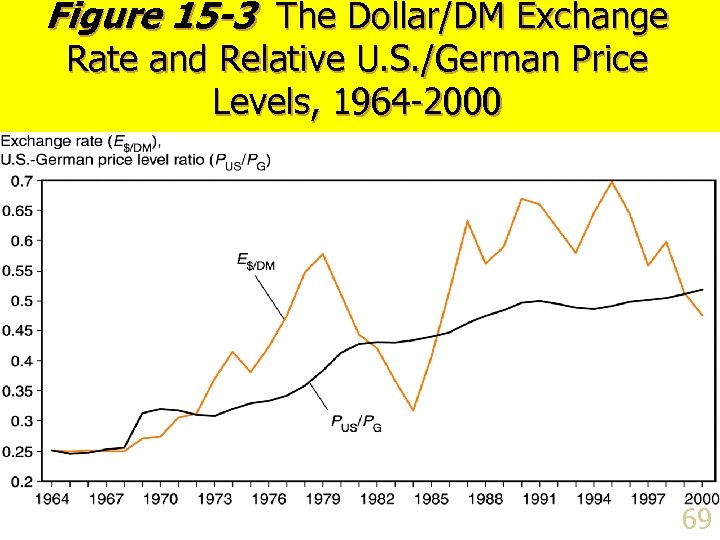Figure 15 -3 The Dollar/DM Exchange Rate and Relative U. S. /German Price Levels, 1964 -2000 69

70

71

72

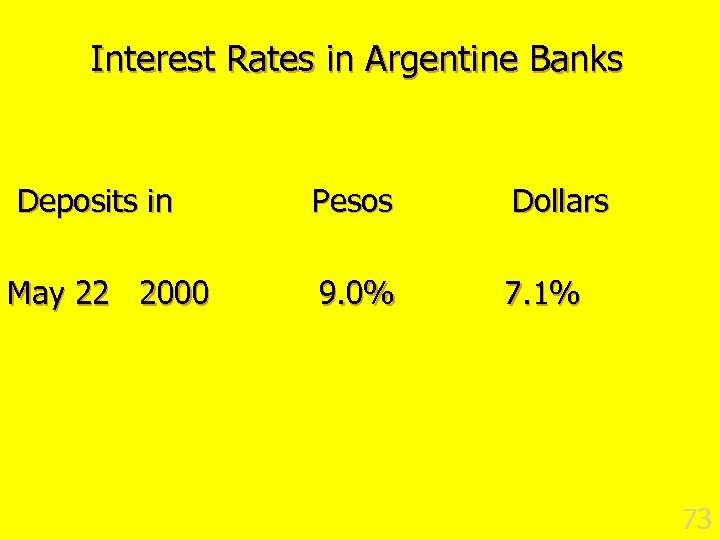Interest Rates in Argentine Banks Deposits in May 22 2000 Pesos Dollars 9. 0% 7. 1% 73

Exchange Rate Risk n Why do peso deposits in Argentine banks pay higher interest than dollar deposits in the same banks? n Exchange risk n Depositors think there is a greater chance of peso depreciation than appreciation 74

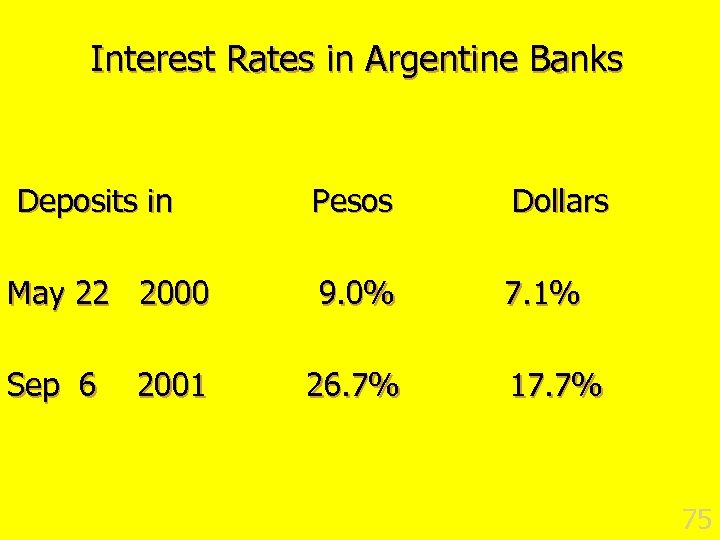Interest Rates in Argentine Banks Deposits in May 22 2000 Sep 6 2001 Pesos Dollars 9. 0% 7. 1% 26. 7% 17. 7% 75

Risk Premium n Why do dollar debts of the Argentine government pay high interest than U. S. debt? n Default risk n Bond holders think there is a greater chance the Argentine government will be unable to repay its debts 76

Risk Premium RPESO = R$ + (EPESO/$e - EPESO/$)/ EPESO/$ + n = risk premium n > 0 for Argentina (compared to U. S. ) n < 0 for U. S. (compared to Argentina) 77