Examples for Discrete Constraint Programming Belaid MOA UVIC, SHRINC Project
Examples n n n n n Map coloring Problem Cryptarithmetic N-queens problem Magic sequence Magic square Zebra puzzle Uzbekian puzzle A tiny transportation problem Knapsack problem graceful labeling problem
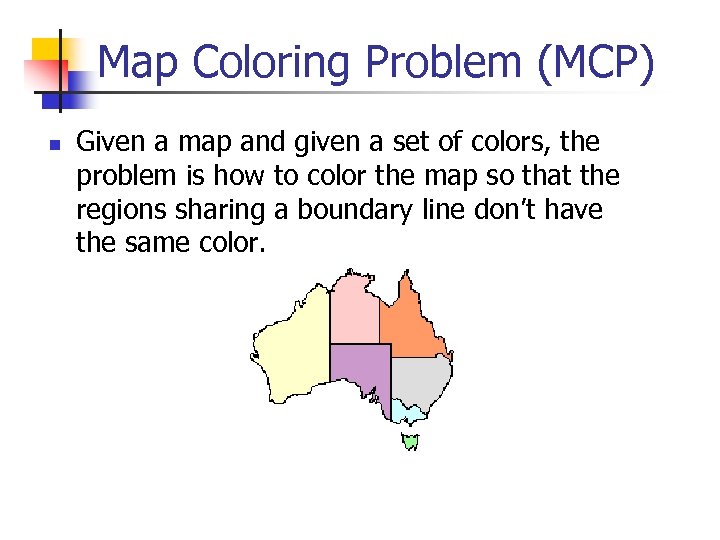
Map Coloring Problem (MCP) n Given a map and given a set of colors, the problem is how to color the map so that the regions sharing a boundary line don’t have the same color.
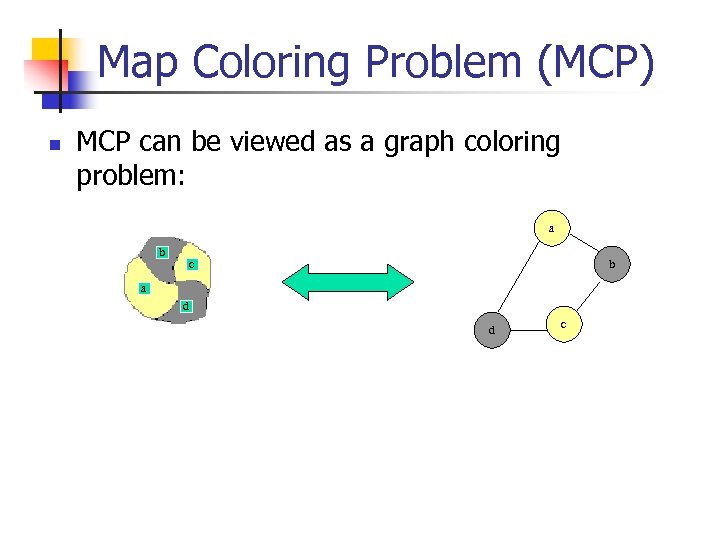
Map Coloring Problem (MCP) n MCP can be viewed as a graph coloring problem: a b c b a d d c
Modeling MCP n MCP can be Modeled as a CSP: n A set of variables representing the color of each region n The domain of the variables is the set of the colors used. n A set of constraints expressing the fact that countries that share the same boundary are not colored with the same color.
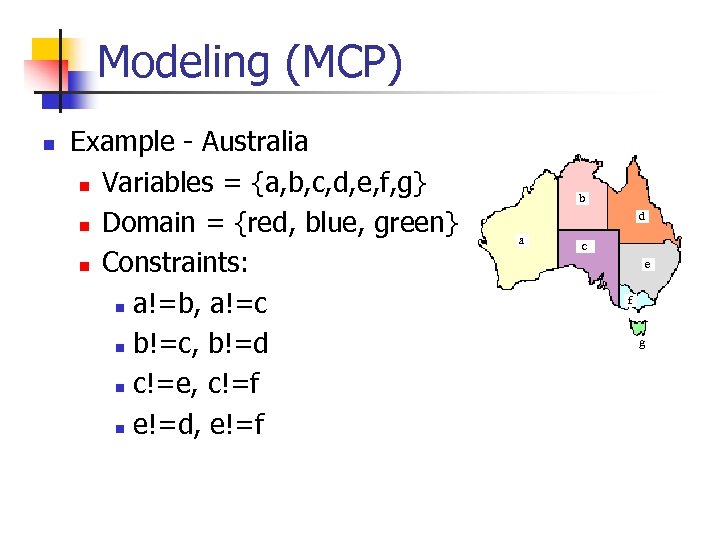
Modeling (MCP) n Example - Australia n Variables = {a, b, c, d, e, f, g} n Domain = {red, blue, green} n Constraints: n a!=b, a!=c n b!=c, b!=d n c!=e, c!=f n e!=d, e!=f b d a c e f g
Coding MCP n OPL studio - Ilog Solver: 54 solutions found enum Country={a, b, c, d, e, f, g}; enum Color = {red, green, blue}; var Color color[Country]; solve{ color[a]<>color[b]; color[a]<>color[c]; color[b]<>color[d]; color[c]<>color[e]; color[c]<>color[f]; color[e]<>color[d]; color[e]<>color[f]; color[b]<>color[c]; color[b]<>color[d]; };
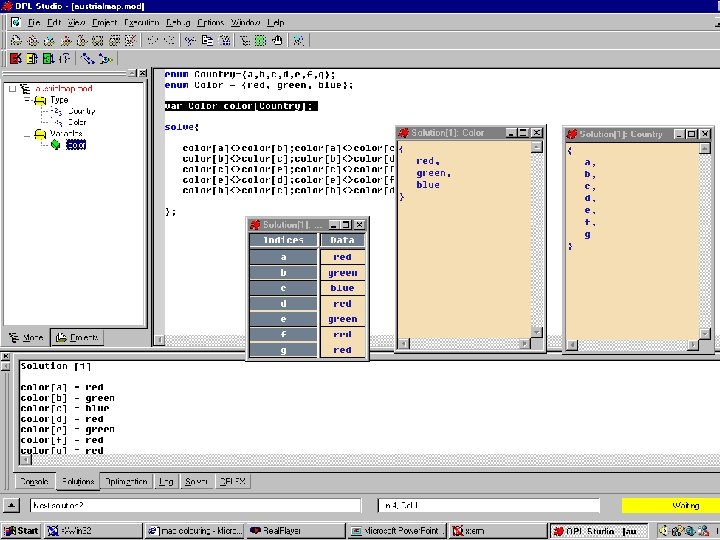
Coding MCP
Coding MCP n ECLi. PSe : - lib(fd). coloured(Countries) : Countries=[A, B, C, D, E, F, G], Countries : : [red, green, blue], ne(A, B), ne(A, C), ne(B, D), ne(C, E), ne(C, F), ne(E, D), ne(E, F), labeling(Countries). ne(X, Y) : - X##Y.
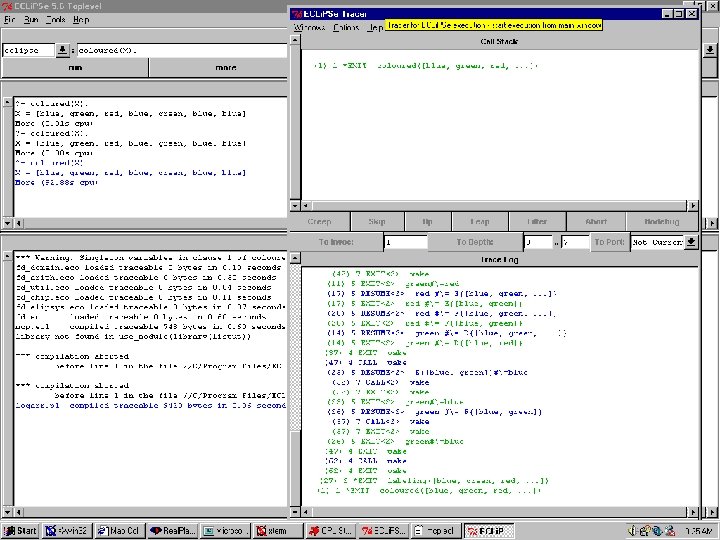
Coding MCP
Cryptarithmetic n The problem is to find the digits corresponding to the letters involved in the following puzzle: SEND + MORE MONEY
Cryptarithmetic Modeling n A CSP model for Cryptarithmetic problem: n Variables={S, E, N, D, M, O, R, Y} n Domain={0, 1, 2, 3, 4, 5, 6, 7, 8, 9} n Constraints n The variables are all different n S!=0, M!=0 3 2 n S*10 +E*10 +N*10+D {SEND} + M*103+O*102+R*10+E {MORE}= M*104+O*103+N*102+E*10+Y {MONEY}
Coding Cryptarithmetic n OPL Studio - ILog Solver enum letter = {S, E, N, D, M, O, R, Y}; range Digit 0. . 9; var Digit value[letter]; solve{ alldifferent(value); value[S]<>0; value[M] <>0; value[S]*1000+value[E]*100+value[N]*10+value[D]+ value[M]*1000+value[O]*100+value[R]*10+value[E] = value[M]*10000+value[O]*1000+value[N]*100+value[E]*10+value[Y] };
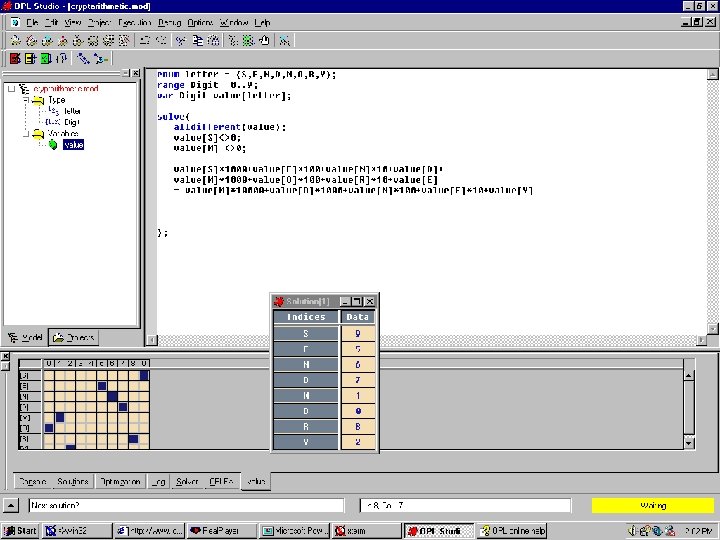
Coding Cryptarithmetic
Coding Cryptarithmetic n ECLi. PSe : - lib(fd). sendmore(Digits) : Digits = [S, E, N, D, M, O, R, Y], Digits : : [0. . 9], alldifferent(Digits), S #= 0, M #= 0, 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E #= 10000*M + 1000*O + 100*N + 10*E + Y, labeling(Digits).
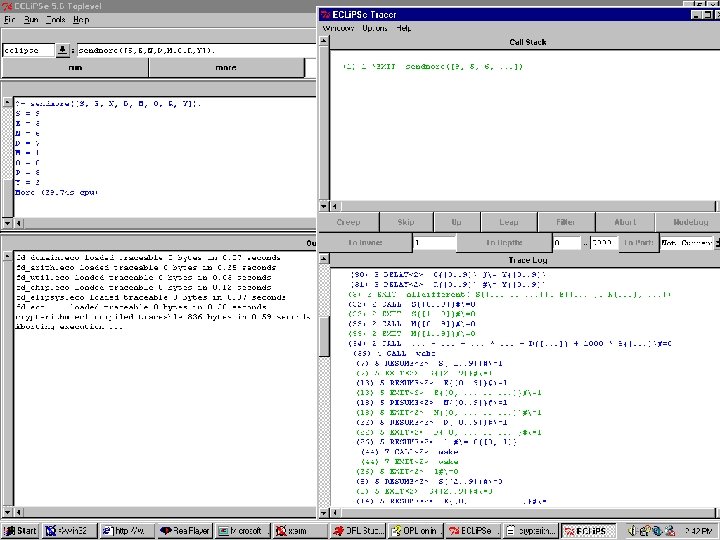
Coding Cryptarithmetic
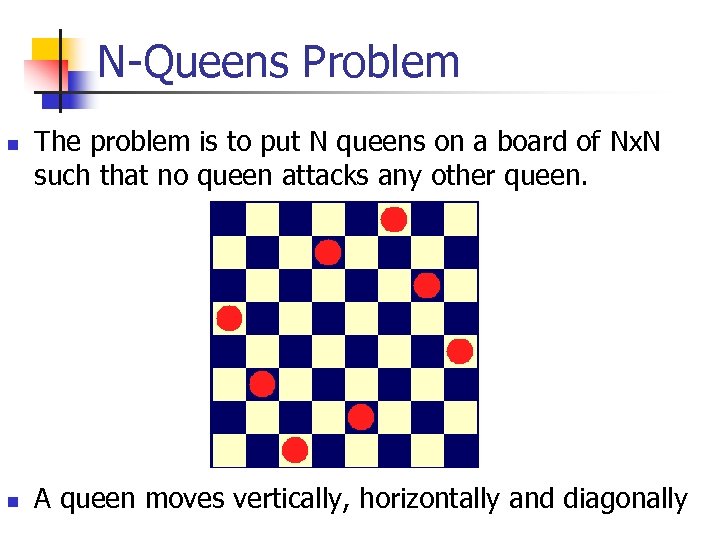
N-Queens Problem n n The problem is to put N queens on a board of Nx. N such that no queen attacks any other queen. A queen moves vertically, horizontally and diagonally
Modeling N-Queens Problem n The queens problem can be modeling via the following CSP n Variables={Q 1, Q 2, Q 3, Q 4, . . . , QN}. n Domain={1, 2, 3, …, N} represents the column in which the variables can be. n Constraints n n n Queens not on the same row: already taken care off by the good modeling of the variables. Queens not on the same column: Qi != Qj Queens not on the same diagonal: |Qi-Qj| != |i-j|
Coding N-Queens Problem n OPL Studio - ILog Solver int n << "number of queens: "; range Domain 1. . n; var Domain queens[Domain]; solve { alldifferent(queens); forall(ordered i, j in Domain) { abs(queens[i]-queens[j])<> abs(i-j) ; }; };
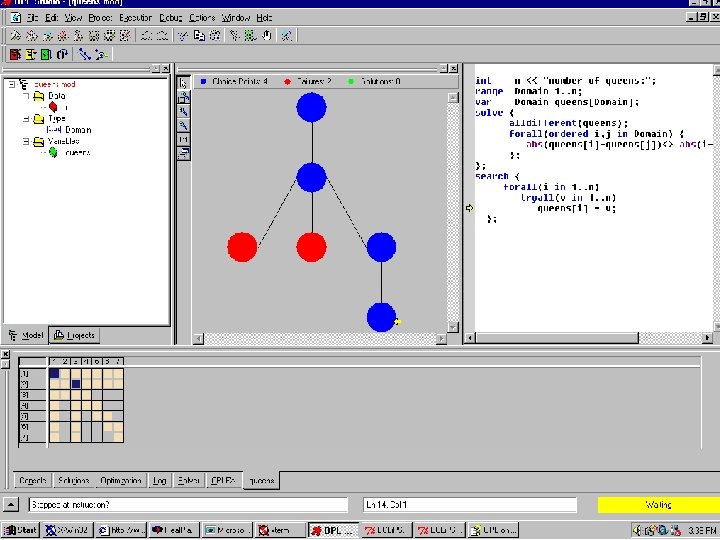
Coding N-Queens Problem
Coding N-Queens Problem n ECLi. PSe : -lib(fd). nqueens(N, Q): length(Q, N), Q: : 1. . N, alldifferent(Q), ( fromto(Q, [Q 1|Cols], Cols, []) do ( foreach(Q 2, Cols), param(Q 1), count(Dist, 1, _) do Q 2 - Q 1 #= Dist, Q 1 - Q 2 #= Dist ) ), search(Q). search([]). search(Q): deleteff(Var, Q, R), indomain(Var), search(R).
Coding N-Queens Problem
Magic sequence problem n n Given a finite integer n, the problem consists of finding a sequence S = (s 0, s 1, …, sn), such that si represents the number of occurrences of i in S. Example: n (2, 0, 2, 0) n (1, 2, 1, 0)
Modeling MSP n MSP can be modeled by the following CSP n variables: s 0, s 1, …, sn-1 n Domain: {0, 1, …, n} n constraints: n n number of occurences of i in (s 0, s 1, …, sn-1) is si. Redundant constraints: n n the sum of s 0, s 1, …, sn-1 is n the sum of i*Si, i in [0. . n-1] is n
Coding MSP n OPL - ILog Solver int n << "Number of Variables: "; range Range 0. . n-1; range Domain 0. . n; int value[i in Range ] = i; var Domain s[Range]; solve { distribute(s, value, s); //global constraint s[i]=sum(j in Range)(s[j]=i) sum(i in Range) s[i] = n; //redundant constraint sum(i in Range) s[i]*i = n; //redundant constraint };
Coding MSP n ECLi. PSe : - lib(fd). : - lib(fd_global). : - lib(fd_search). solve(N, Sequence) : length(Sequence, N), Sequence : : 0. . N-1, ( for(I, 0, N-1), foreach(Xi, Sequence), foreach(I, Range), param(Sequence) do occurrences(I, Sequence, Xi) ), N #= sum(Sequence), % two redundant constraints N #= Sequence*Range, search(Sequence, 0, first_fail, indomain, complete, []). %search procedure
Magic square problem n n A magic square of size N is an Nx. N square filled with the numbers from 1 to N 2 such that the sums of each row, each column and the two main diagonals are equal. Example:
Modeling Magic square pb n Magic square problem can be viewed as a CSP with the following properties: n Variables: the elements of the matrix representing the square n Domain: 1. . N*N n Constraints: n magic sum = sum of the columns = sum of the rows = sum of the down diagonal = sum of the up diagonal n Remove symmetries n Redundant constraint: n magic sum = N(N 2+1)/2
Coding Magic square pb n OPL Studio: int N << "The length of the square: "; range Dimension 1. . N; range Values 1. . N*N; int msum = N*(N*N+1)/2; //magic sum var Values square[1. . N, 1. . N]; solve { //The elements of the square all different alldifferent(square); //the sum of the diagonal is magic sum msum = sum(i in Dimension)square[i, i]; //the sum of the up diagonal is magic sum
![Coding Magic square pb msum = sum(i in Dimension)square[i, N-i+1]; //the sum of the](https://present5.com/presentation/51def67efe508fa2cb74ebf90fdccb7b/image-30.jpg "Coding Magic square pb msum = sum(i in Dimension)square[i, N-i+1]; //the sum of the")
Coding Magic square pb msum = sum(i in Dimension)square[i, N-i+1]; //the sum of the rows and columns are all magic sum forall(i in Dimension){ msum = sum(j in Dimension)square[i, j]; msum = sum(k in Dimension)square[k, i]; }; //remove symmetric behavior of the square[N, 1] < square[1, N]; square[1, 1] < square[N, 1]; };
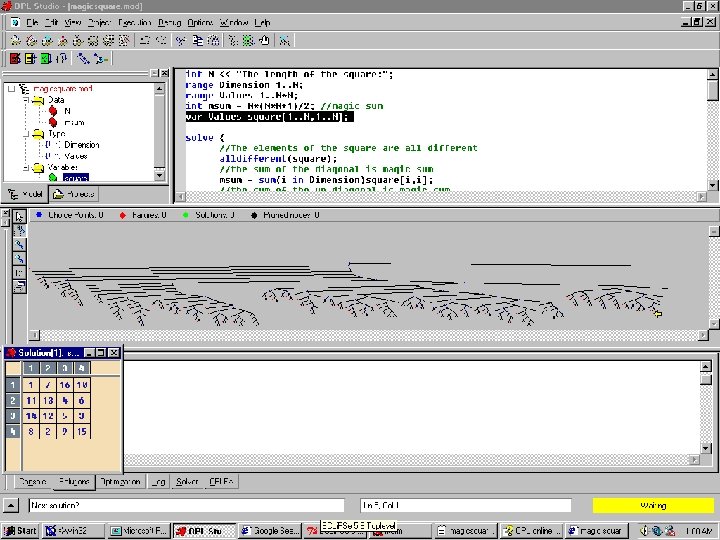
Magic square problem
Coding Magic square pb n ECLi. PSe: : - lib(fd). magic(N) : Max is N*N, Magicsum is N*(Max+1)//2, dim(Square, [N, N]), Square[1. . N, 1. . N] : : 1. . Max, Rows is Square[1. . N, 1. . N], flatten(Rows, Vars), alldifferent(Vars),
Coding Magic square pb %constraints on rows ( for(I, 1, N), foreach(U, Up. Diag), foreach(D, Down. Diag), param(N, Square, Sum) do Magicsum #= sum(Square[I, 1. . N]), Magicsum #= sum(Square[1. . N, I]), U is Square[I, I], D is Square[I, N+1 -I] ), %constraints on diagonals Magicsum #= sum(Up. Diag), Magicsum #= sum(Down. Diag),
![Coding Magic square pb %remove symmetry Square[1, 1] #< Square[1, N], Square[1, 1] #<](https://present5.com/presentation/51def67efe508fa2cb74ebf90fdccb7b/image-34.jpg "Coding Magic square pb %remove symmetry Square[1, 1] #< Square[1, N], Square[1, 1] #<")
Coding Magic square pb %remove symmetry Square[1, 1] #< Square[1, N], Square[1, 1] #< Square[N, 1], Square[1, N] #< Square[N, 1], %search labeling(Vars), print(Square). Unfortunately, ECLi. PSe ran for a long time without providing any answer. ECLi. PSe had also the same behavior for a similar code from ECLi. PSe website.
A Tiny Transportation problem n How much should be shipped from several sources to several destinations Supply cpty a 1 a 2 : am Source 1 Demand Qty Shipped Destination Qty x 1 n x 12 2 x 21 x 22 x 2 n : m x 11 1 b 1 2 : n b 2 : bn
A Tiny Transportation problem n 3 plants with known capacities, 4 clients with known demands and transport costs per unit between them. 500 1 1 200 300 2 Find qty shipped? 2 400 3 300 4 100 400 3
Modeling TTP n TTP can be modeled by a CSP with optimization as follows: n n n Variables: A 1, A 2, A 3, B 1, B 2, B 3, C 1, C 2, C 3, D 1, D 2, D 3 Domain: 0. 0. . Inf constraints: n Demand constraints: A 1+A 2+A 3=200; B 1+B 2+B 3=400; C 1+C 2+C 3=300; D 1+D 2+D 3=100; n Capacity constraints: A 1+B 1+C 1+D 1 500; A 2+B 2+C 2+D 2 300; A 3+B 3+C 3+D 3 400; n Minimization of the objective function: 10*A 1 + 7*A 2 + 11*A 3 + 8*B 1 + 5*B 2 + 10*B 3 + 5*C 1 + 5*C 2 + 8*C 3 + 9*D 1 + 3*D 2 + 7*D 3
![Coding TTP n OPL Studio - Cplex Solver var float+ product. A[Range]; var float+](https://present5.com/presentation/51def67efe508fa2cb74ebf90fdccb7b/image-38.jpg "Coding TTP n OPL Studio - Cplex Solver var float+ product. A[Range]; var float+")
Coding TTP n OPL Studio - Cplex Solver var float+ product. A[Range]; var float+ product. B[Range]; var float+ product. C[Range]; var float+ product. D[Range]; minimize 10*product. A[1] + 7*product. A[2] + 11*product. A[3] + 8*product. B[1] + 5*product. B[2] + 10*product. B[3] + 5*product. C[1] + 5*product. C[2] + 8*product. C[3] + 9*product. D[1] + 3*product. D[2] + 7*product. D[3] subject to { product. A[1] + product. A[2] + product. A[3] = 200; product. B[1] + product. B[2] + product. B[3] = 400; product. C[1] + product. C[2] + product. C[3] = 300; product. D[1] + product. D[2] + product. D[3] = 100; product. A[1] + product. B[1] + product. C[1] + product. D[1]<=500 product. A[2] + product. B[2] + product. C[2]+product. C[2] <= 300; product. A[3] + product. B[3] + product. C[3] + product. D[3] <= 400; };
Coding TTP n OPL Studio - Cplex Solver: Solution found Optimal Solution with Objective Value: 6200. 0000 product. A[1] = 100. 0000 product. A[2] = 0. 0000 product. A[3] = 100. 0000 product. B[1] = 100. 0000 product. B[2] = 300. 0000 product. B[3] = 0. 0000 product. C[1] = 300. 0000 product. C[2] = 0. 0000 product. C[3] = 0. 0000 product. D[1] = 0. 0000 product. D[2] = 100. 0000 product. D[3] = 0. 0000
Coding TTP n ECLi. PSe : - lib(eplex_cplex). main 1(Cost, Vars) : Vars = [A 1, A 2, A 3, B 1, B 2, B 3, C 1, C 2, C 3, D 1, D 2, D 3], Vars : : 0. 0. . inf, A 1 + A 2 + A 3 $= 200, B 1 + B 2 + B 3 $= 400, C 1 + C 2 + C 3 $= 300, D 1 + D 2 + D 3 $= 100, A 1 + B 1 + C 1 + D 1 $=< 500, A 2 + B 2 + C 2 + D 2 $=< 300, A 3 + B 3 + C 3 + D 3 $=< 400, optimize(min(10*A 1 + 7*A 2 + 11*A 3 + 8*B 1 + 5*B 2 + 10*B 3 + 5*C 1 + 5*C 2 + 8*C 3 +9*D 1 + 3*D 2 + 7*D 3), Cost). It didn’t run! calling an undefined procedure cplex_prob_init(…)
Zebra puzzle n n Zebra is a well known puzzle in which five men with different nationalities live in the first five house of a street. They practice five distinct professions, and each of them has a favorite animal and a favorite drink, all of them different. The five houses are painted in different colors. The puzzle is to find who owns Zebra puzzle has different statements. We’ll handle two. This kind of Puzzle is usually treated as an instance of the class of tabular constraint satisfaction problems in which we express the problem using tables. In this presentation we show to solve it using CSP languages: OPL studio and ECLi. PSe.
Modeling Zebra puzzle n In crucial step in Modeling Zebra puzzle is finding the decision variables. In our case, we consider: n variables: persons, colors, pets, drinks, tobaccos. n Domain: 1. . 5 (representing the five houses) n Constraints: Expressed directly from the statement of the puzzle.
Coding Zebra puzzle n OPL Studio - ILog Solver enum people {Englishman, Spaniard, Ukrainian, Norwegian, Japanese}; enum drinks {coffee, tea, milk, orange, water}; enum pets {dog, fox, zebra, horse, snails}; enum tabacco {winston, kools, chesterfields, lucky. Strike, parliaments }; enum colors {ivory, yellow, red , green, blue}; range houses 1. . 5; //{first, second, third, fourth, fifth}; var houses hse. Clr[colors]; var houses hse. Pple[people]; var houses hse. Pts[pets]; var houses hse. Drks[drinks]; var houses hse. Taba[tabacco];
![Coding Zebra puzzle solve{ hse. Pple[Englishman] = hse. Clr[red]; hse. Pple[Spaniard]=hse. Pts[dog]; hse. Drks[coffee]](https://present5.com/presentation/51def67efe508fa2cb74ebf90fdccb7b/image-44.jpg "Coding Zebra puzzle solve{ hse. Pple[Englishman] = hse. Clr[red]; hse. Pple[Spaniard]=hse. Pts[dog]; hse. Drks[coffee]")
Coding Zebra puzzle solve{ hse. Pple[Englishman] = hse. Clr[red]; hse. Pple[Spaniard]=hse. Pts[dog]; hse. Drks[coffee] = hse. Clr[green]; hse. Pple[Ukrainian] = hse. Drks[tea]; hse. Clr[green] = hse. Clr[ivory]+1; hse. Taba[winston] = hse. Pts[snails]; hse. Taba[kools]=hse. Clr[yellow]; hse. Drks[milk]=3; hse. Pple[Norwegian] = 1; hse. Taba[chesterfields]=hse. Pts[fox]+1 / hse. Taba[chesterfields]=hse. Pts[fox]-1; hse. Taba[kools] = hse. Pts[horse]+1 / hse. Taba[kools] = hse. Pts[horse]-1 ; hse. Taba[ lucky. Strike] = hse. Drks[orange]; hse. Pple[ Japanese] = hse. Taba[parliaments]; hse. Pple[Norwegian] = hse. Clr[blue]+1 / hse. Pple[Norwegian] = hse. Clr[blue]-1; //slient constraints-Global constraint alldifferent(hse. Pple); //forall(ordered i, j in people) hse. Pple[i] <> hse. Pple[j]; alldifferent(hse. Pts); //forall(ordered i, j in pets) hse. Pts[i] <> hse. Pts[j]; alldifferent(hse. Clr); //forall(ordered i, j in colors) hse. Clr[i] <> hse. Clr[j]; alldifferent(hse. Drks); //forall(ordered i, j in drinks) hse. Drks[i] <> hse. Drks[j]; alldifferent(hse. Taba); //forall(ordered i, j in tabacco) hse. Taba[i] <> hse. Taba[j]; };
Coding Zebra puzzle % The Englishman lives in a red house. % The Spaniard owns a dog. % The Japanese is a painter. % The Italian drinks tea. % The Norwegian lives in the first house on the left. % The owner of the green house drinks coffee. % The green house is on the right of the white one. % The sculptor breeds snails. % The diplomat lives in the yellow house. % Milk is drunk in the middle house. % The Norwegian's house is next to the blue one. % The violinist drinks fruit juice. % The fox is in a house next to that of the doctor. % The horse is in a house next to that of the diplomat. % % Who owns a Zebra, and who drinks water? %
Coding Zebra puzzle : - lib(fd). zebra : % we use 5 lists of 5 variables each Nat = [English, Spaniard, Japanese, Italian, Norwegian], Color = [Red, Green, White, Yellow, Blue], Profession = [Painter, Sculptor, Diplomat, Violinist, Doctor], Pet = [Dog, Snails, Fox, Horse, Zebra], Drink = [Tea, Coffee, Milk, Juice, Water], % domains: all the variables range over house numbers 1 to 5 Nat : : 1. . 5, Color : : 1. . 5, Profession : : 1. . 5, Pet : : 1. . 5, Drink : : 1. . 5,
Coding Zebra puzzle % the values in each list are exclusive alldifferent(Nat), alldifferent(Color), alldifferent(Profession), alldifferent(Pet), alldifferent(Drink), % and here follow the actual constraints English = Red, Spaniard = Dog, Japanese = Painter, Italian = Tea, Norwegian = 1, Green = Coffee, Green #= White + 1, Sculptor = Snails, Diplomat = Yellow, Milk = 3, Dist 1 #= Norwegian - Blue, Dist 1 : : [-1, 1], Violinist = Juice, Dist 2 #= Fox - Doctor, Dist 2 : : [-1, 1], Dist 3 #= Horse - Diplomat, Dist 3 : : [-1, 1],
Coding Zebra puzzle % put all the variables in a single list flatten([Nat, Color, Profession, Pet, Drink], List), % search: label all variables with values labeling(List), % print the answers: we need to do some decoding Nat. Names = [English-english, Spaniard-spaniard, Japanese-japanese, Italian-italian, Norwegian-norwegian], memberchk(Zebra-Zebra. Nat, Nat. Names), memberchk(Water-Water. Nat, Nat. Names), printf("The %w owns the zebra%n", [Zebra. Nat]), printf("The %w drinks water%n", [Water. Nat]). Answer from ECLi. PSe after 0. 02 s The japanese owns the zebra The norwegian drinks water
Uzbekian Puzzle An uzbekian sales man met five traders who live in five different cities. The five traders are: n {Abdulhamid, Kurban, Ruza, Sharaf, Usman} The five cities are : n {Bukhara, Fergana, Kokand, Samarkand, Tashkent} n Find the order in which he visited the cities given the following information: n n n He met Ruza before Sharaf after visiting Samarkand, He reached Fergana after visiting Samarkand followed by other two cities, The third trader he met was Tashkent, Immediately after his visit to Bukhara, he met Abdulhamid He reached Kokand after visiting the city of Kurban followed by other two cities;
Modeling Uzbekian Puzzle n The uzbekian puzzle can formulated within the CSP framework as follows: n Variables: order in which he visited each city and met each trader n Domain: 1. . 5 n constraints: n n n He met Ruza before Sharaf after visiting Samarkand, He reached Fergana after visiting Samarkand followed by other two cities, The third trader he met was Tashkent, Immediately after his visit to Bukhara, he met Abdulhamid He reached Kokand after visiting the city of Kurban followed by other two cities;
Coding Uzbekian Puzzle in OPL enum cities {Bukhara, Fergana, Kokand, Samarkand, Tashkent}; enum traders {Abdulhamid, Kurban, Ruza, Sharaf, Usman}; range order 1. . 5; var order mt. Trader[traders]; var order vst. Cty[cities]; Solution [1] solve{ mt. Trader[Ruza] < mt. Trader[Sharaf]; mt. Trader[Abdulhamid] = 2 mt. Trader[Ruza] > vst. Cty[Samarkand]; mt. Trader[Kurban] = 3 vst. Cty[Fergana] = vst. Cty[Samarkand] + 2; mt. Trader[Ruza] = 4 vst. Cty[Tashkent] = 3; mt. Trader[Sharaf] = 5 mt. Trader[Abdulhamid] = vst. Cty[Bukhara] + 1; mt. Trader[Usman] = 1 vst. Cty[Kokand] = mt. Trader[Kurban] + 2; alldifferent(mt. Trader); vst. Cty[Bukhara] = 1 alldifferent(vst. Cty); vst. Cty[Fergana] = 4 }; vst. Cty[Kokand] = 5 vst. Cty[Samarkand] = 2 vst. Cty[Tashkent] = 3
Knapsack problem n n We have a knapsack with a fixed capacity and a number of items. Each item has a weight and a value. The problem consists of filling the knapsack without exceeding its capacity, while maximizing the overall value of its contents. Knapsack problem is an example of Mixed integer programming.
Modeling Knapsack problem n A CSP model for knapsack problem is given by: n n Variables: For each item, we associate a variable that gives the quantity of such an item we can put in the knapsack. Domain: 0. . Capacity of the knapsack Constraints: n sum of the weights in the knapsack is less than the capacity Objective function to maximize: n sum of the values in the knapsack
Coding Knapsack Pb in OPL range items 1. . 10; int Max. Capacity= 1000; int value[items] = [29, 30, 25, 27, 28, 21, 23, 19, 18, 17]; int weight[items] =[30, 32, 33, 31, 34, 40, 45, 44, 39, 35]; var int take[items] in 0. . Max. Capacity; maximize sum(i in items) value[i] * take[i] subject to sum(i in items) weight[i] * take[i] <= Max. Capacity; integer programming (CPLEX MIP) displaying solution. . . take[1] = 28 take[2] = 5 take[i] = 0, i=3. . 10
Graceful labeling problem n n Given a tree T with m+1 nodes, and m edges, find the possible labels in {0, 1, …, m} for the nodes such that the absolute value of the difference of the labels of the nodes related to each edge are all different. Formally, let f be a function from V ----> {0, …, m}, where V is the set of the vertices of T. n f is said to be a graceful labeling of T iff n |f(vi)-f(vj)| are all different for any edge vivj in T.
Modeling Graceful labeling Pb n Graceful labeling problem can be formulated into the following CSP: n variables: labels to put on each node of T n Domain: 0. . m n constraints: n the absolute value of the difference between the labels of any edge are all different
Coding Graceful labeling Pb n OPL program for graceful labeling problem int nbre. Of. Nodes =. . . ; //set the range of the labels of the nodes range nodes 0. . nbre. Of. Nodes-1; range indices 1. . nbre. Of. Nodes; int adjacency. Matrix[indices, indices] =. . . ; var nodes label[indices]; solve { alldifferent(label); forall(ordered i, j in indices){ if(adjacency. Matrix[i, j] <> 0) then forall(ordered k, h in indices){ if(adjacency. Matrix[k, h] <> 0 & not(k=i & h=j)) then abs(label[i]-label[j])<>abs(label[h]-label[k]) endif; }; };
Coding Graceful labeling Pb n Data file nbre. Of. Nodes = 7; adjacency. Matrix = [ 1, 0, [ 0, 1, [ 0, 0, 1, 0, [ 0, 0, n 1 [[ 0, 0, 1, 1, 0, 0, 0, 1, Solution Example: 1, 0, 0, 0], 0 ], 5 1 ], 0 ]]; label[1] = 0 label[2] = 6 label[3] = 1 label[4] = 3 label[5] = 4 label[6] = 5 label[7] = 2 2 3 4 6 7
Скачать презентацию Examples for Discrete Constraint Programming Belaid MOA UVIC
51def67efe508fa2cb74ebf90fdccb7b.ppt