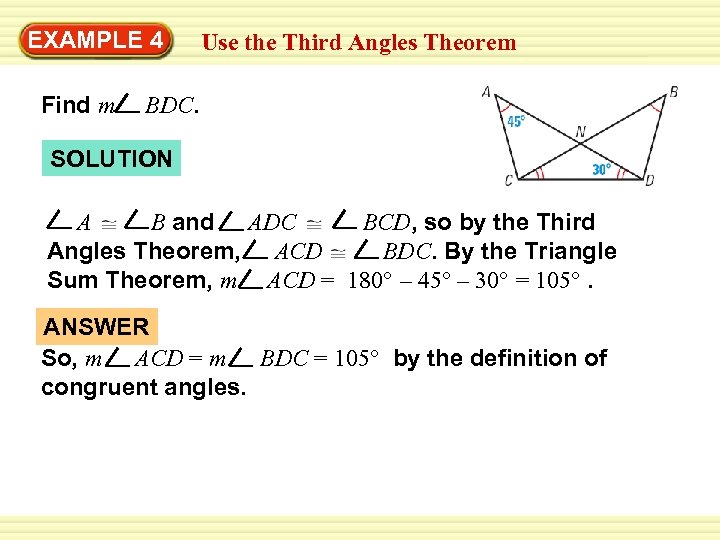
EXAMPLE 4 Find m Use the Third Angles

EXAMPLE 4 Find m Use the Third Angles Theorem BDC. SOLUTION A B and ADC BCD, so by the Third Angles Theorem, ACD BDC. By the Triangle Sum Theorem, m ACD = 180° – 45° – 30° = 105°. ANSWER So, m ACD = m BDC = 105° by the definition of congruent angles.

EXAMPLE 5 Prove that triangles are congruent Write a proof. GIVEN AD CB, DC ACD PROVE AB CAB, ACD CAD ACB CAB Plan for Proof a. Use the Reflexive Property to show that AC AC. b. Use the Third Angles Theorem to show that B D

EXAMPLE 5 Prove that triangles are congruent Plan in Action STATEMENTS REASONS 1. AD CB, DC a. 2. AC AC. 3. b. 4. 5. ACD CAD B ACD BA 1. Given 2. Reflexive Property of Congruence CAB, ACB D 3. Given 4. Third Angles Theorem CAB 5. Definition of

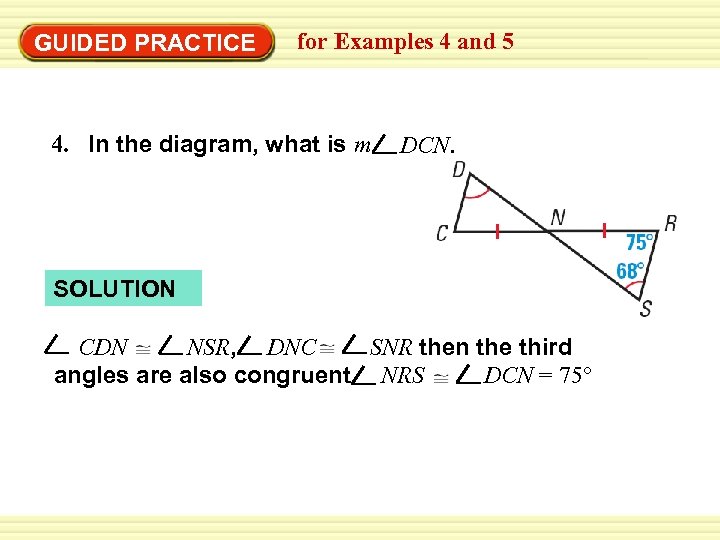GUIDED PRACTICE for Examples 4 and 5 4. In the diagram, what is m DCN. SOLUTION CDN NSR, DNC SNR then the third angles are also congruent NRS DCN = 75°

GUIDED PRACTICE for Examples 4 and 5 5. By the definition of congruence, what additional information is needed to know that NDC NSR. SOLUTION Given : CN NR, DCN Proved : NDC CDN NRS NSR, (Proved from above sum)

GUIDED PRACTICE for Examples 4 and 5 STATEMENT REASON CDN NSR Given DCN NRS Given Therefore DC RS, DN SN as angles are congruent their sides are congruent.