d94545e77c18f4cd43b2df3a07eb1cd8.ppt
- Количество слайдов: 129

Exam Review Created by Noah Freund 14 May 2010 Algebra 1

st Power Equations Solving 1 with One Variable

Solving 1 st Power Equations in One Variable The object of 1 st power equations is to find the value of the variable (x, a, f). Here are the steps to get there: - Find a way to get the variable by its self on one side of the equal sign by doing the opposite of what is placed on in the equation (we will do more of this in the commutative property) x + 3=7 x + 3 - 3=7 - 3 x=4

st 1 Power Equations (cont. ) Sometimes you may need to do more than just add or subtract, you will sometimes need to divide and multiply. Just keep doing the opposite of what the equation says. x * 3 = 27 x * 3 / 3 = 27 / 3 x = 9 y/2 = 12 y/2 * 2 = 12 * 2 y = 24

1 st Power Equations (cont. more) Sometimes, you may have an equation with the variable on both sides of the equation. Make sure you get both variables on one side. x*2=2 -x (x + x) * 2 = 2 - x + x 2 x * 2 = 2 2 x = 1 x = ½

st 1 Power Equations (cont. ) Sometimes, in special occasions, you will get a answer where the variables cancel out each other. If the both sides of the equal sign are equal, then any real number can be the variable. If not, then it’s nulset. x – 3 = x – 4 + 1 -3 = -3 {allreals} x – 3 = x – 4 -3 -4

1 st Power Equations (cont. some more) Other times, there will be fractions in the equation containing the variable. Just multiply by the denominator in order for the variable to be a whole number, therefore, you can factor out the value of the variable.

1 st Power Equations (cont. even more) Sometimes, the exponent will be in the denominator of a fraction. When this happens, you multiply the equation by the variable in the denominator.

Properties

Addition Property (of Equality) If X = Y, then X+5 = Y+5 Multiplication Property (of Equality) If X = Y, then X*3 = Y*3

Reflexive Property (of Equality) Simply, X = X Symmetric Property (of Equality) If X = Y, then Y = X Transitive Property (of Equality) If X = Y and Y = Z, then X = Z

Associative Property of Addition If (X+Y)+Z = B, then (Z+X)+Y = B Associative Property of Multiplication If (X*Y)*Z = A, then (Z*X)*Y = A

Commutative Property of Addition (X+Y+Z) = A, so (Z+X+Y) = A Commutative Property of Multiplication (X*Y*Z) = A, so (Z*X*Y) = A

Distributive Property (of Multiplication over Addition) If X*(Y+Z) = A, then XY+XZ = A

Prop of Opposites or Inverse Property of Addition X + -X = 0 Prop of Reciprocals or Inverse Prop. of Multiplication

Identity Property of Addition X+0 = X Identity Property of Multiplication X*1 = X

Multiplicative Property of Zero X*0 = 0 Closure Property of Addition If X and Y is a real numbers then X + Y = Z, then Z is a real number Closure Property of Multiplication If X and Y is a real numbers then X + Y = Z, then Z is a real number

Product of Powers Property XY * AB = (A*X)Y+B Power of a Product Property (X*Y)Z = XZ *YZ Power of a Power Property (X 2)2 = (X)2*2 = X 4

Quotient of Powers Property Power of a Quotient Property

Zero Power Property If (X+Y)*(A-B) = 0 Then (X+Y) = 0 or (A – B) = 0 So, X =-Y and/or A = B

Negative Power Property

Zero Product Property 0 X =1

Product of Roots Property Quotient of Roots Property

Root of a Power Property Power of a Root Property

Quiz Time! Give the name of the property shown. Click when you’re ready to see the answer. 1. A = B, B = C, so A = C Answer: Transitive Property of Equality

More Quiz! Look at the problem and give the name of the property shown. Click when you’re ready to see the answer. 2. X * 1 = X Answer: Identity Property of Multiplication

Solving 1 st Power Inequalities with One Variable.

Solving Inequalities with one Variable Solving Inequalities is just like solving equaions. The difference here is that there is either a ‘greater’ or ‘less than’ sign instead of an equal sign. Equation: x-3 = 2 Inequality: x-3 > 2

If you multiply or divide by a negative, you must reverse the inequality sign. -2 x < 4 x > -2 Solution Set: {x: x > -2} Graph of the Solution: -2
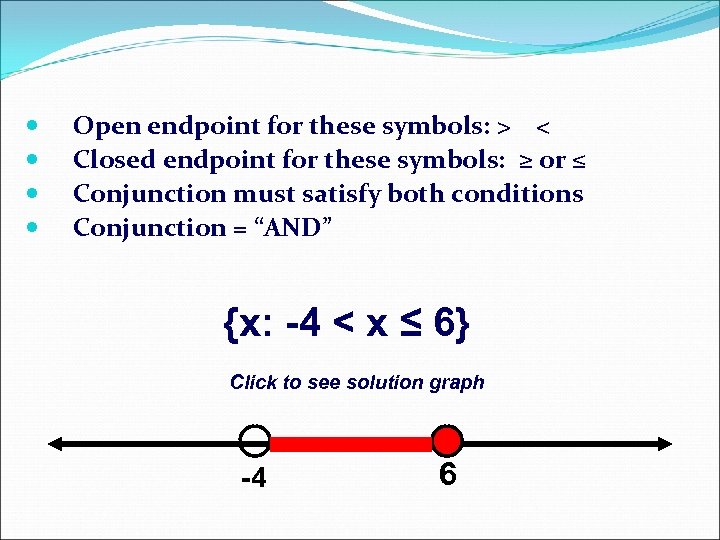
Open endpoint for these symbols: > < Closed endpoint for these symbols: ≥ or ≤ Conjunction must satisfy both conditions Conjunction = “AND” {x: -4 < x ≤ 6} Click to see solution graph -4 6

Open endpoint for these symbols: > < Closed endpoint for these symbols: ≥ or ≤ Disjunction must satisfy either one or both of the conditions Disjunction = “OR” {x: x < -2 or x ≥ 3} Click to see solution graph -2 3

Watch for special cases No solutions that work: Answer is Ø Every number works: Answer is {reals} Disjunction in same direction: answer is one arrow {x: x > -2 or x ≥ 3} Click to see solution graph -2 3

Watch for special cases No solutions that work: Answer is Ø Every number works: Answer is {reals} Disjunction in same direction: answer is one arrow {x: -x < -2 and -5 x ≥ 15} Click to see solution Ø
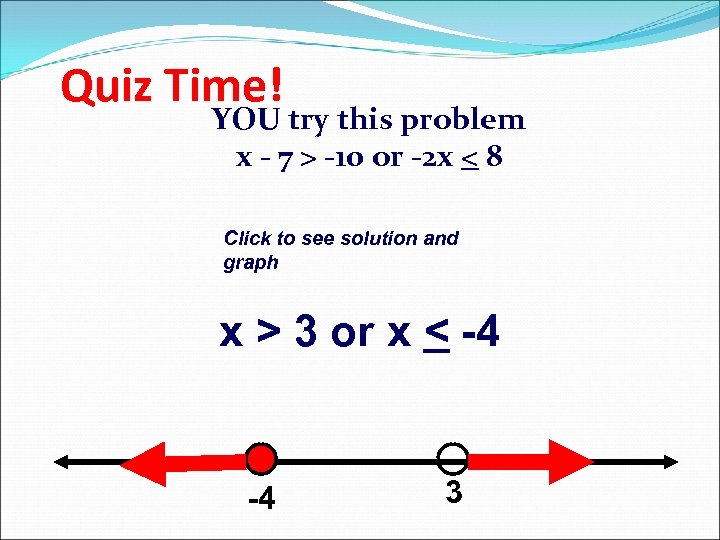
Quiz Time! YOU try this problem x - 7 > -10 or -2 x < 8 Click to see solution and graph x > 3 or x < -4 -4 3

Linear Equations with Two Variables

Standard and Point-Slope Form The equation; 4 x - 2 y = -4 is in standard form. You can tell because of the way it is ordered. Standard form will always be; Ax + By = C The equation y = 2 x + 4 is the same equation, only in Point-Slope form. The point slope form always goes; y = mx + b. This way is profitable, because it tells you the slope and the y-intercept. m = slope b = y-intercept

Slopes If it is a positive slope, the line will rise up from left to right and if negative it will run down Slopes are in a form where the rise (vertical) is on top (do this first) and the run (horizontal) on the bottom. What would you move if the slope was 1/5? You would move 1 up and 5 to the right

How to Find Intercepts are the places where the line crosses the yaxis or x-axis. To find these in an equation, you set the variable you are not looking for to zero. EX: 3 x – 2 y = 25 3(0) – 2 y = 25 y = -12. 5 3 x – 2 y = 25 -2 y = 25 3 x – 2(0) = 25 3 x = 25 x = 8. 33333. .

How To Graph When graphing, it’s easier to use the point slope form, since the slope and y-intercept are given to you already. -3 y = -2 x + 3 y = 2/3 x + 0 2 x – 3 y = 3 Hint: If there is no value of number for this place the only intercepts the origin.
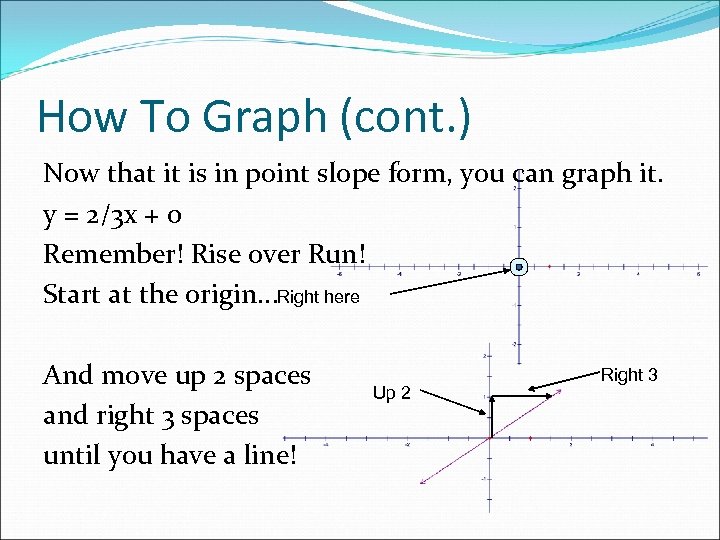
How To Graph (cont. ) Now that it is in point slope form, you can graph it. y = 2/3 x + 0 Remember! Rise over Run! Start at the origin. . . Right here And move up 2 spaces and right 3 spaces until you have a line! Up 2 Right 3

Linear Systems

Substitution Method When given an equation with 2 different variables, you can use this method. Knowing the value of one variable, you can substitute that one for its value. x + 3 = y – 7 and 2 x + y = 40 x + 3 = y – 7 is the same as x = y – 10, so if we plug it into the other equation, it will look like; 2(y – 10) + y = 40 2 y + y – 20 = 40 3 y = 60 y = 20 That being said; x = 20 – 10 x = 10

Addition or Subtraction Method This method takes the two equations and adds or subtracts them together until one of the variables has cancelled out. 3 x + 6 y = 22 and 6 x + 8 y = 46 Multiply this one by two so we can subtract the ‘x’ variable out. 2(3 x + 6 y = 22) 6 x + 12 y = 22

Addition and Subtraction (cont. ) Then subtract the two equations together, 6 x + 12 y = 22 -6 x + 8 y = 46 0 x + 4 y = 68 y = 17 We then plug it into an equation to get the other variable 3 x + 6(17) = 22 3 x + 102 = 22 3 x = -80 x = 26 and 2/3

Consistency is when two equations are exactly the same. The Substitution method would work best. EX: 3 x + y = 5 and 3 x + y = 5 they are both the same Dependent is when the equations are in relation with each other. They are multiples of each other or sums or differences of each other. If an equation is Independent, then you should use the addition subtraction method EX: 3 x + y = 5 and 6 x + 2 y = 10 are dependent because the second one is the first multiplied by two.

Factoring

Factoring is using methods to make problems more simple. Using various properties, you can cut down on the amount of ink you use while making it easier to multiply by other things.

Factoring: Reverse Foil Just like foiling, but the opposite. You take a trinomial and turn it into a set of binomials x 2 + 3 x + 4 (x + 4)(x – 1) Because… x*x = x 2 x*-1 = -x Firsts Outsides x*4 = 4 x Insides 4*-1 = -4 Lasts

Factoring: PST is short for perfect square trinomial. You take a PST and change it into 2 binomials. (x 2 – 36) (x – 6)(x + 6) Because. . . x*x = x 2 x*6 = 6 x x*-6 = -6 x 6*-6 = -36

Factoring: GCF is short for Greatest Common Factor. You take the greatest number (or glob) you can from a equation. (2 x + 6)*(3 z + 7) 2(x + 3)* z(3 + 7)

Factoring: Difference of Squares Finding the difference of squares involves taking 2 square numbers (or globs) and breaking it down into 2 conjugates. 4 x 2 – 36 x 4 (2 x – 6 x 2) (2 x + 6 x 2) IMPORTANT!!!! You CAN NOT perform difference of squares on positive numbers

Factoring: Difference of Cubes Difference of cubes is a way to turn a cubed glob into a binomial and a trinomial Finally, take the opposite X 3 – 8 (x – 2) 2 + 2 x + 4) (x of the product of the binomial, and place it in the middle First, take the cube roots of both the numbers Then, take the square of those numbers and place them on both sides

Factoring: Factoring the GCF of the problem by Grouping Factoring by grouping is taking and taking the result further by finding another common glob. (3 x 2 – 2 x) + (9 x 2 – 6 x) x(3 x - 2) + 3 x(3 x – 2) (x + 3 x)

Factoring: Special Case In some cases, you will have to use both the difference of squares and the difference of cubes. X 6 – 729 z 6 Difference of Squares (x 3 – 27 z 3)(x 3 + 27 z 3) (x – 9 z)(x 2 + 9 xz + 81 z 2) (x + 9 z)(x 2 – 9 xz + 81 z 2) Difference of Cubes

Functions

What the Heck does f(X) Mean? f(x) simply means ‘y’ Instead of the equation to graph being something like; y = 9 x + 2, it’s now f(x) = 9 x + 2 In other words, they are completely the same and do not have different functions at all

Domain and Range The domain is the set of inputs or ‘x’ values that you put into an equation The range is the output or the ‘y’ value of an equation y=2 x+1 Here’s a example: x y 2 5 1 3 0 1 -1 -1

Finding 2 a Line on a Graph Given 2 Points When given points on a graph, you can find the line quite easily. First you use the slope formula; ‘m’ being the slope Then you can use this formula to find the yintercept

Finding a Line on a Graph Given 2 Points (cont. ) Here is an example with real numbers: Using the points (2, -3) and (4, 5) when graphed it looks like this:

Quadratics If you find the domains and ranges of a equation like y = x 2 + x, you will see that the line will curve upward like so. This is a parabola. There is nothing wrong with what it’s doing, it’s just structured that way x 1 0 -1 -3 y 2 1 1 8
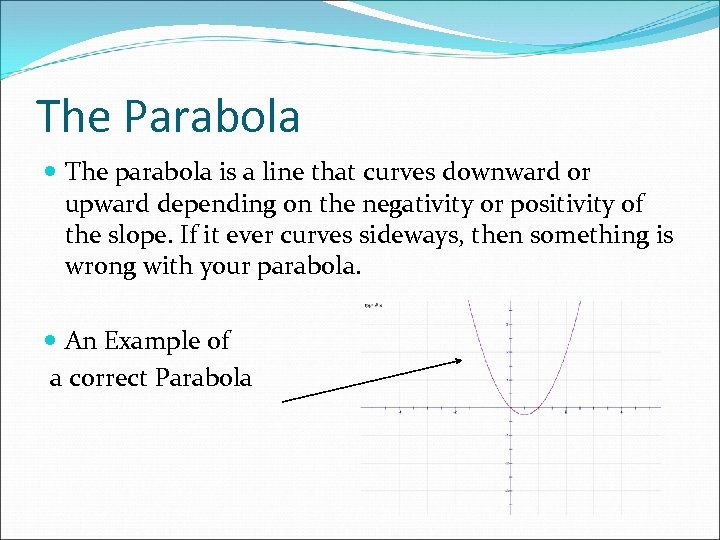
The Parabola The parabola is a line that curves downward or upward depending on the negativity or positivity of the slope. If it ever curves sideways, then something is wrong with your parabola. An Example of a correct Parabola

Using this graph to represent the parabola, we will look at the parts of the parabola. The vertex is the point where there is only one line with that y value The intercepts help you locate where on the graph in relation to the origin. The line of symmetry that splits the middle. It crosses the vertex

• To find x-intercepts: – the parabola may have Zero, One or Two xintercepts 1. Set ‘y’ or "f(x)" to zero on one side of the equation 2. Factor & use the Zero Product Prop to find TWO x-intercepts To find y-intercept, set x = 0. Note f(0) will equal c. I. E. (0, c) The equations following this will use ‘a’ and ‘b’. Any quadratic equation will have ax 2 + bx + c = f(x) d. To find the coordinates of the vertex (turning pt): 1. x-coordinate of the vertex comes from this formula: 2. plug that x-value into the function to find the y-coordinate e. The axis of symmetry is the vertical line through vertex: x =

Now You Try! Find the Vertex, Line of symmetry, y and x intercepts for this equation: f(x) = x 2 – 2 x – 8 Vertex The vertex is the ordered pair, (-1, -9) Y-intersept f(x) = x 2 – 2 x – 8 f(x) = (0)2 – 2(0) – 8 f(x) = 0 – 8 f(x) = -8

X intercept f(x) = x 2 – 2 x – 8 0 = (x – 4)(x + 2) The x intercepts are (4, 0) and (-2, 0)

Quadratic Equations in One Variable

METHOD 1 - FACTORING Set equal to zero Factor Use the Zero Product Property to solve (Each factor with a variable in it could be equal to zero. )

METHOD 1 - FACTORING Any # of terms – Look for GCF factoring first! 1. 5 x 2 = 15 x 5 x 2 – 15 x = 0 5 x (x – 3) = 0 5 x = 0 OR x – 3 = 0 x = 0 OR x = 3 {0, 3}

METHOD 1 - FACTORING Binomials – Look for Difference of Squares 2. x 2 = 9 x 2 – 9 = 0 (x + 3) (x – 3) = 0 Conjugates x + 3 = 0 OR x – 3 = 0 x = – 3 OR x = 3 {– 3, 3}

METHOD 1 - FACTORING Trinomials – Look for PST (Perfect Square Trinomial) 3. x 2 – 8 x = – 16 x 2 – 8 x + 16 = 0 (x – 4) = 0 x – 4 = 0 OR x – 4 = 0 x = 4 OR x = 4 {4 d. r. } Double Root

METHOD 1 - FACTORING Trinomials – Look for Reverse of Foil 4. 2 x 3 – 15 x = 7 x 2 2 x 3 – 7 x 2 – 15 x = 0 (x) (2 x 2 – 7 x – 15) = 0 {-3/2, 0, 5} (x) (2 x + 3)(x – 5) = 0 x = 0 OR 2 x + 3 = 0 OR x – 5 = 0 x = 0 OR x = – 3/2 OR x = 5

METHOD 2 – SQUARE ROOTS OF BOTH SIDES Reorder terms IF needed Works whenever form is (glob)2 = c Take square roots of both sides (Remember you will need a sign!) Simplify the square root if needed Solve for x. (Isolate it. )

METHOD 2 – SQUARE ROOTS OF BOTH SIDES 1. 2 x =9 x= 3 {-3, 3} Note means both +3 and -3! x = -3 OR x = 3

METHOD 2 – SQUARE ROOTS OF BOTH SIDES 2. x 2 = 18

METHOD 2 – SQUARE ROOTS OF BOTH SIDES 3. 2 x =– 9 Cannot take a square root of a negative. There are NO real number solutions!

METHOD 2 – SQUARE ROOTS OF BOTH SIDES 4. 2 (x-2) =9 {-1, 5} This means: x = 2 + 3 and x = 2 – 3 x = 5 and x = – 1

METHOD 2 – SQUARE ROOTS OF BOTH SIDES Rewrite as (glob)2 = c first if necessary. 2 – 10 x + 25 = 9 5. x (x – 2 5) =9 {2, 8} x = 8 and x = 2

METHOD 2 – SQUARE ROOTS OF BOTH SIDES Rewrite as (glob)2 = c first if necessary. 2 – 10 x + 25 = 48 6. x (x – 5)2 = 48

METHOD 3 – COMPLETE THE SQUARE • • • The goal is to get into the format: (glob)2 = c Method always works, but is only recommended when a = 1 or all the coefficients are divisible by a We will practice this method repeatedly and then it will keep getting easier!

METHOD 3 – COMPLETE THE SQUARE Example: 3 x 2 – 6 = x 2 + 12 x 2 x 2 – 12 x – 6 = 0 Simplify and write in standard form: ax 2 + bx + c = 0 x 2 – 6 x – 3 = 0 Set a = 1 by division Note: in some problems a will already be equal to 1.

METHOD 3 – COMPLETE THE SQUARE x 2 – 6 x – 3 = 0 x 2 – 6 x =3 x 2 – 6 x + 9 = 3 + 9 (x – 3)2 = 12 Move constant to other side Leave space to replace it! Add (b/2)2 to both sides This completes a PST! Rewrite as (glob)2 = c

METHOD 3 – COMPLETE THE SQUARE 2 = 12 (x – 3) Take square roots of both sides – don’t forget Simplify Solve for x

METHOD 4 – QUADRATIC FORMULA • • • Works to solve all quadratic equations Rewrite in standard form in order to identify the values of a, b and c. Plug a, b & c into the formula and simplify! • QUADRATIC FORMULA:

METHOD 4 – QUADRATIC FORMULA Use to solve: 3 x 2 – 6 = x 2 + 12 x Standard Form: 2 x 2 – 12 x – 6 = 0

METHOD 4 – QUADRATIC FORMULA

QUADRATIC FUNCTIONS a. The graph is a parabola. Opens up if a > 0 and down if a < 0. b. To find x-intercepts: – may have Zero, One or Two x-intercepts 1. Set y or "f(x)" to zero on one side of the equation 2. Factor & use the Zero Product Prop to find TWO x-intercepts c. To find y-intercept, set x = 0. Note f(0) will equal c. I. E. (0, c) d. To find the coordinates of the vertex (turning pt): 1. x-coordinate of the vertex comes from this formula: 2. plug that x-value into the function to find the y-coordinate e. The axis of symmetry is the vertical line through vertex: x =

QUADRATIC FUNCTIONS Example Problem: f(x) = x 2 – 2 x – 8 a. Opens UP (positive) b. x-intercepts: 0 = x 2 – 2 x – 8 0 = (x – 4)(x + 2) (4, 0) and (– 2, 0) c. y-intercept: f(0) = (0)2 – 2(0) – 8 (0, – 8) d. vertex: e. axis of symmetry: x = 1

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES 1. 2 x = 121 x = 11 {-11, 11} Note means both +11 and -11! x = -11 OR x = 11

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES 2. x 2 = – 81 Cannot take a square root of a negative. There are NO real number solutions!

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES Rewrite as (glob)2 = c first if necessary. 2 = 156 3. 6 x 2 x = 26

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES 4. (a – 7)2 = 3

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES Rewrite as (glob)2 = c first if necessary. 5. 9(x 2 – 14 x + 49) = 4 (x – 7)2 = 4/9 {6⅓, 7⅔}

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES

PRACTICE METHOD 3 – COMPLETE THE SQUARE Example: 2 b 2 = 16 b + 6 2 b 2 – 16 b – 6 = 0 Simplify and write in standard form: ax 2 + bx + c = 0 b 2 – 8 b – 3 = 0 Set a = 1 by division Note: in some problems a will already be equal to 1.

PRACTICE METHOD 3 – COMPLETE THE SQUARE b 2 – 8 b – 3 = 0 b 2 – 8 b =3 – 8 b + 16 = 3 +16 (b – 4)2 = 19 Move constant to other side Leave space to replace it! Add (b/2)2 to both sides This completes a PST! Rewrite as (glob)2 = c

PRACTICE METHOD 3 – 2 = 19 COMPLETE THE SQUARE (b – 4) Take square roots of both sides – don’t forget Simplify Solve for the variable

PRACTICE METHOD 3 – COMPLETE THE SQUARE Example: 3 n 2 + 19 n + 1 = n - 2 3 n 2 + 18 n + 3 = 0 Simplify and write in standard form: ax 2 + bx + c = 0 n 2 + 6 n + 1 = 0 Set a = 1 by division Note: in some problems a will already be equal to 1.

PRACTICE METHOD 3 – COMPLETE THE SQUARE n 2 + 6 n + 1 = 0 n 2 + 6 n = -1 n 2 Move constant to other side Leave space to replace it! 2 + 6 n + 9 = -1 + 9 Add (b/2) to both sides This completes a PST! (n + 3)2 = 8 Rewrite as (glob)2 = c

PRACTICE METHOD 3 – (n + 3)2 = 8 COMPLETE THE SQUARE Take square roots of both sides – don’t forget Simplify Solve for the variable

PRACTICE METHOD 3 – COMPLETE THE SQUARE What number “completes each square”? 1. x 2 – 10 x = -3 1. x 2 – 10 x + 25 = -3 + 25 2. x 2 + 14 x =1 2. x 2 + 14 x + 49 = 1 + 49 3. x 2 – 1 x =5 3. x 2 – 1 x + ¼ = 5 + ¼ 4. 2 x 2 – 40 x =4 4. x 2 – 20 x + 100 = 2 + 100

PRACTICE METHOD 3 – COMPLETE THE SQUARE Now rewrite as (glob)2 = c 1. x 2 – 10 x + 25 = -3 + 25 1. (x – 5)2 = 22 2. x 2 + 14 x + 49 = 1 + 49 2. (x + 7)2 = 50 3. x 2 – 1 x + ¼ = 5 + ¼ 3. (x – ½ )2 = 5 ¼ 4. x 2 – 20 x + 100 = 2 + 100 4. (x – 10)2 = 102

PRACTICE METHOD 3 – COMPLETE THE SQUARE Show all steps to solve. ⅓k 2 = 4 k - ⅔ 2 = 12 k - 2 k k 2 - 12 k =-2 2 - 12 k + 36 = - 2 + 36 k 2 = 34 (k - 6)

PRACTICE METHOD 4 – QUADRATIC FORMULA Show all steps to solve & simplify. 2 x 2 = x + 6 2 x 2 – x – 6 =0

PRACTICE METHOD 4 – QUADRATIC FORMULA Show all steps to solve & simplify. x 2 + x + 5 = 0

PRACTICE METHOD 4 – QUADRATIC FORMULA Show all steps to solve & simplify. 2 +2 x x -4=0

THE DISCRIMINANT – MAKING PREDICTIONS b 2 – 4 ac is called the discriminant Four cases: 1. b 2 – 4 ac positive non-square two irrational roots 2 – 4 ac positive square two rational roots 2. b 3. b 2 – 4 ac 4. zero one rational double root 2 – 4 ac negative no real roots b

THE DISCRIMINANT – MAKING PREDICTIONS Use the discriminant to predict how many “roots” each equation will have. 1. x 2 – 7 x – 2 = 0 49– 4(1)(-2)=57 2 irrational roots 2. 0 = 2 x 2– 3 x + 1 9– 4(2)(1)=1 2 rational roots 3. 0 = 5 x 2 – 2 x + 3 4– 4(5)(3)=-56 no real roots 4. 100– 4(1)(25)=0 1 rational double root x 2 – 10 x + 25=0

THE DISCRIMINANT – MAKING PREDICTIONS about Parabolas The “zeros” of a function are the x-intercepts on it’s graph. Use the discriminant to predict how many x-intercepts each parabola will have and where the vertex is located. 1. y = 2 x 2 – x - 6 1– 4(2)(-6)=49 2 rational zeros 2. f(x) = 2 x 2 – x + 6 1– 4(2)(6)=-47 no real zeros 3. y = -2 x 2– 9 x + 6 4. f(x) = x 2 – 6 x + 9 81– 4(-2)(6)=129 2 irrational zero 36– 4(1)(9)=0 one rational

THE DISCRIMINANT – MAKING PREDICTIONS Note! The “zeros” of a function are the x-intercepts on it’s graph. Use the discriminant to predict how many x-intercepts the parabola will have. The “roots” of an equation are the x values that make the expression equal to zero. Equations have roots. Functions have zeros which are the x-intercepts on it’s graph.

FOUR METHODS – HOW DO I CHOOSE? Some suggestions: Quadratic Formula – works for all quadratic equations, but first look for a “quicker” method. You must rewrite into standard form before using Quad Formula! Don’t forget to simplify square roots and use value of the discriminant to predict the number of roots or zeros. Square Roots of Both Sides – use when the problem can easily be put into the form: glob 2 = constant. Examples: 3(x + 2)2=12 or x 2 – 75 = 0

FOUR METHODS – HOW DO I CHOOSE? Some suggestions: Factoring – doesn’t always work, but IF you can see the factors, this is probably the quickest method. Examples: x 2 – 8 x = 0 has a GCF 4 x 2 – 12 x + 9 = 0 is a PST x 2 – x – 6 = 0 is easy to FOIL Complete the Square – It always works, but if you aren’t quick at arithmetic with fractions, then this method is best used when a = 1 and b is even (so no fractions). Example: x 2 – 6 x + 1 = 0

QUADRATIC FORMULA – Derive it by Completing the Square! Start with Standard Form: ax 2 + bx + c = 0

Simplifying Expressions with Exponents

Simplifying Expressions with Exponents Using the Product of Powers Property: x 2 * y 3 * z 7 * z 5 = x 7 y 3 z 7 Using the Power of a Product Property: (x * y / z)4 = (x 4 y 4)/z 4 Using the Power of a Power Property: (x 3 * y 2 / z 7)4 = (x 12 y 8)/z 28

Quotient of Powers: Power of a Quotient: Zero Power Property:

Negitive Power Property: Root of a Power Property: Power of a Root Property:

Simplifying Expressions with Radicals

Factor and Cancel with Irrational numbers The expression; is not simplified all the way. you can divide 18 into 9 and 2. Since 9 is a square, you can get the square root of that and put it on the outside of the radical sign.

Addition and Subtraction of Radicals You can add and subtract radicals also. However, them must have the same number inside the radicals and can not be added with numbers without radicals. Remember! You can’t add radicals with whole numbers!

Multiplication of Radicals You may also multiply and divide radicals. Using the equation; , you can see that you just take what is inside the radical and multiply it with the others.

Word Problems for you to Try on your Own!

Word Problem 1: Jan has gotten a 92, 72, 83, 98, and 88 on her tests. What Is the average? What is the median? 72, 83, 88, 92, 98 92 72 85 middle number 98 +88 Average = 87 435 Median = 88

Word Problem 2 The sum of a two digit numeral is 11. when the digits are reversed, the new number is 63 less than the original. What is the original number? Tens = t t + x = 11 – t Ones = x 10 t + x = 10 x + t + 63 The number is 92 10 t + 11 – t = 10(11 – t) + t + 63 9 t + 11 = 110 – 9 t + 63 9 t + 11 = 173 – 9 t 18 t = 162 t = 9 so, 9 + x = 11 x = 2

Word Problem 3 A price of electrical wire varies directly as the square of its length in meters. If a 5 meter length of wire costs $75, find: 1) What is the equation that represents the price to length 2) The number of meters of wire you can buy with $1200 75 = 25 k 3 = k 75 =5 * 25 1) 75 = k*52 the equation is Cost = Modifier * Length 2

Word Problem 3 (cont. ) Cost = Modifier * Length 2 2) 1200 = 3 L 2 C = ML 2 400 = L 2 +20 = L You can buy 20 meters of wire with $1200

Word Problem 4 You have a combination of 33 dimes and quarters worth six dollars. How many dimes do you have? # of dimes = d d + q = 33 # of quarters = q d = 33 – q 10 d + 25 q = 600 10 d + 25(33 – d) = 600 There are 15 dimes 10 d + 825 – 25 d = 600 and 18 quarters -15 d = -225 d = 15 15 + q = 33 q = 18

Line of Best Fit or Regression Line

When do you use a Best Fit Line? You use a best fit line on a scatter-plot graph. The best fit line can be used to find the average of the points in the scatter plot graph. The Ti-84 Calculator can help you do this. You just need to enter the points into the graph so that you get a visual aid to estimate form. It also can draw the line for you.

Find the Best Fit Line! Here is a scatter plot graph that you get to find the best fit line. Since you can’t use a calculator (there are no numbers) try to find it manually (hint: try squinting. You may see an imaginary line). click to find an approximate line
d94545e77c18f4cd43b2df3a07eb1cd8.ppt