Эвольвентные поверхности ГОУ ВПО ИНЭКА Курс лекций по

Эвольвентные поверхности ГОУ ВПО ИНЭКА Курс лекций по дисциплине: «Основы теории режущих инструментов»

Эвольвентные поверхности в деталях машин Цилиндрические зубчатые колеса Прямозубые – Эвольвентная цилиндрическая поверхность Косозубые – Эвольвентная винтовая поверхность Конические прямозубые колеса – Эвольвентная коническая поверхность

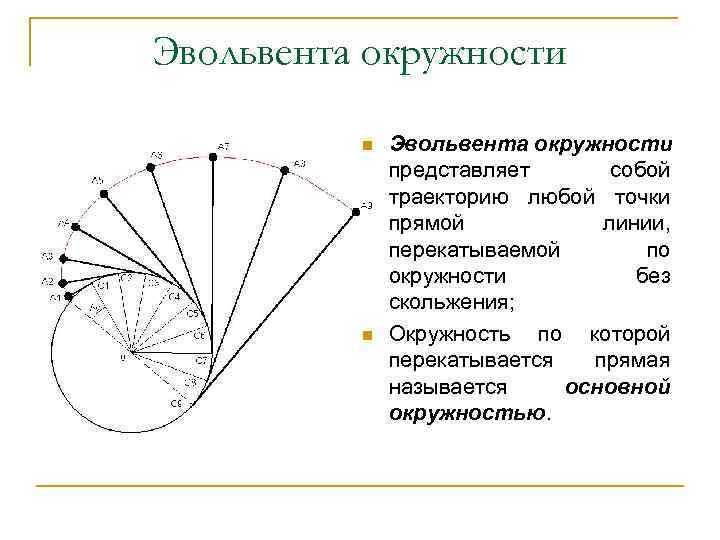Эвольвента окружности n n Эвольвента окружности представляет собой траекторию любой точки прямой линии, перекатываемой по окружности без скольжения; Окружность по которой перекатывается прямая называется основной окружностью.

Образование эвольвенты окружности

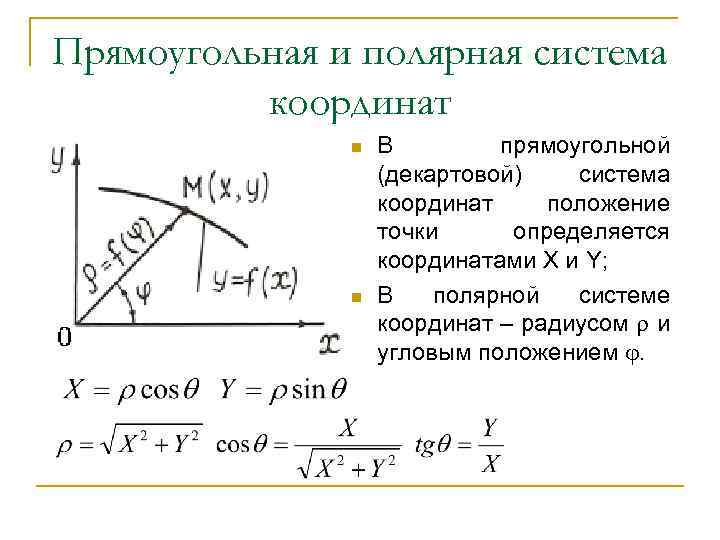Прямоугольная и полярная система координат n n В прямоугольной (декартовой) система координат положение точки определяется координатами X и Y; В полярной системе координат – радиусом и угловым положением .

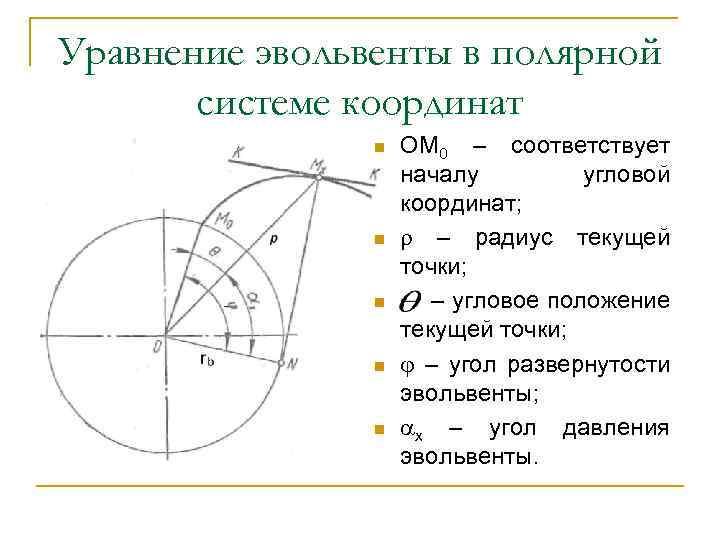Уравнение эвольвенты в полярной системе координат n n n ОМ 0 – соответствует началу угловой координат; – радиус текущей точки; – угловое положение текущей точки; – угол развернутости эвольвенты; х – угол давления эвольвенты.

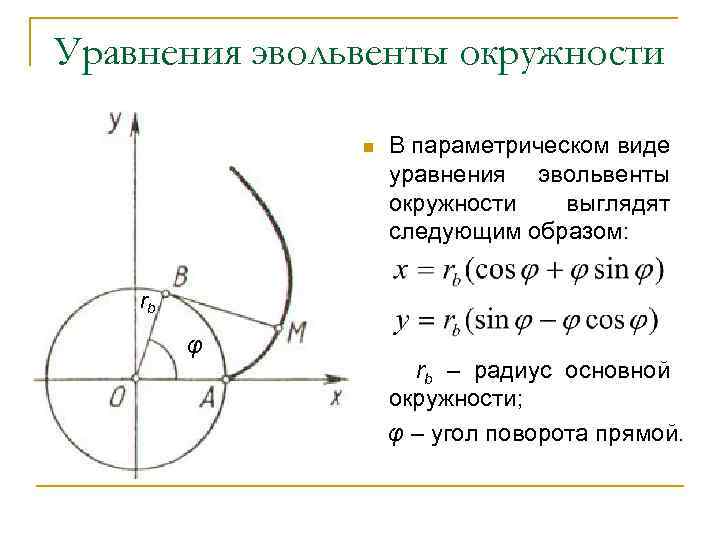Уравнения эвольвенты окружности n В параметрическом виде уравнения эвольвенты окружности выглядят следующим образом: rb φ rb – радиус основной окружности; φ – угол поворота прямой.

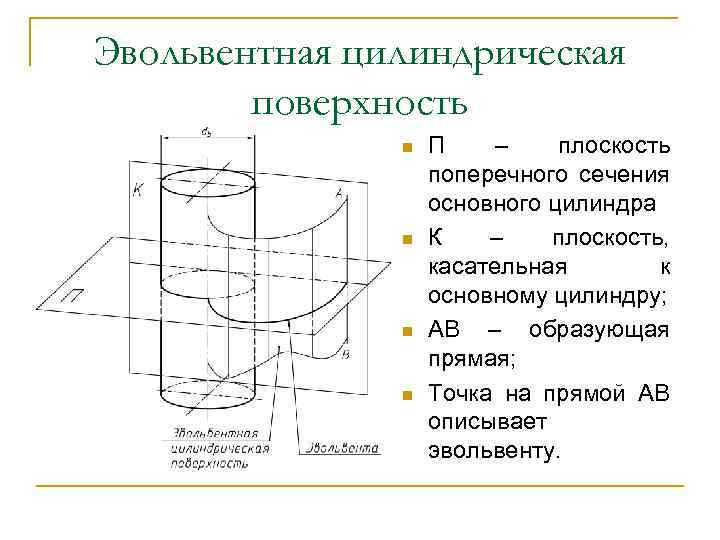Эвольвентная цилиндрическая поверхность n n П – плоскость поперечного сечения основного цилиндра К – плоскость, касательная к основному цилиндру; АВ – образующая прямая; Точка на прямой АВ описывает эвольвенту.

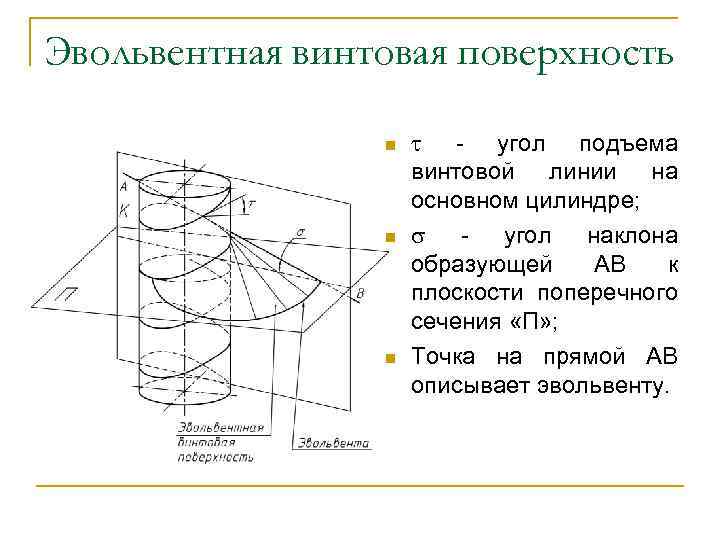Эвольвентная винтовая поверхность n n n - угол подъема винтовой линии на основном цилиндре; - угол наклона образующей АВ к плоскости поперечного сечения «П» ; Точка на прямой АВ описывает эвольвенту.

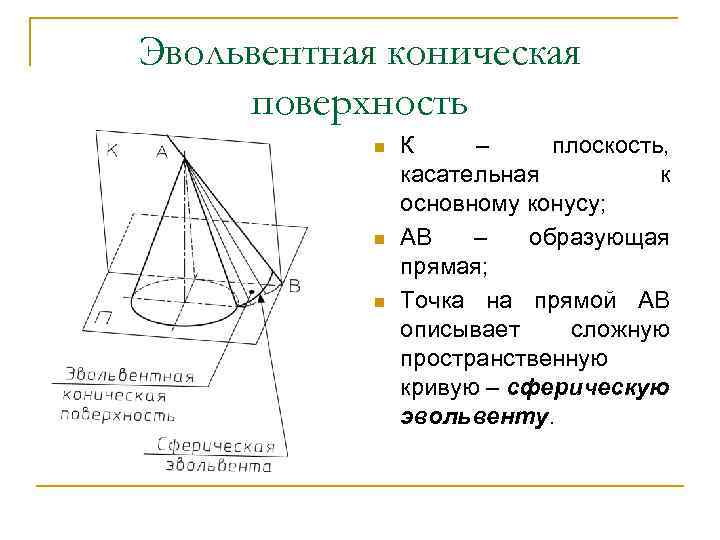Эвольвентная коническая поверхность n n n К – плоскость, касательная к основному конусу; АВ – образующая прямая; Точка на прямой АВ описывает сложную пространственную кривую – сферическую эвольвенту.

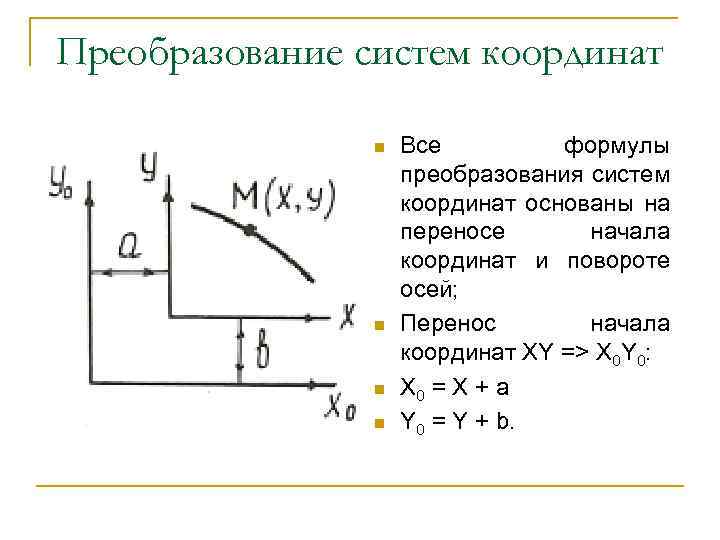Преобразование систем координат n n Все формулы преобразования систем координат основаны на переносе начала координат и повороте осей; Перенос начала координат XY => X 0 Y 0: Х 0 = Х + а Y 0 = Y + b.

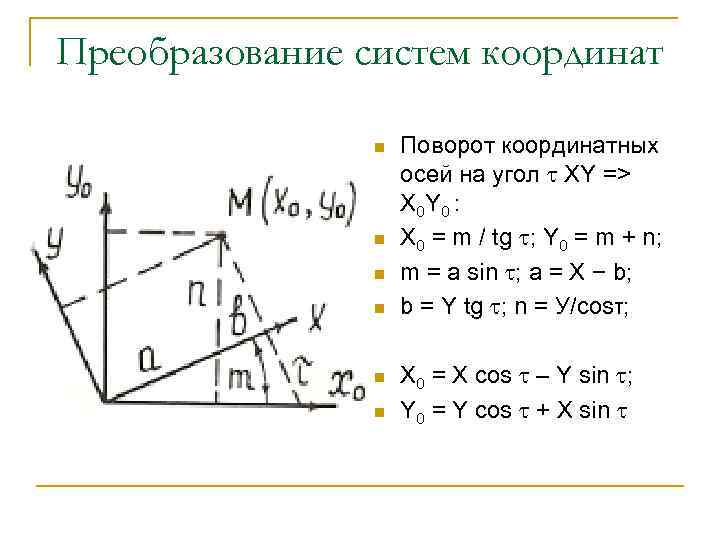Преобразование систем координат n n n Поворот координатных осей на угол XY => X 0 Y 0 : Х 0 = m / tg ; Y 0 = m + n; m = a sin ; a = Х − b; b = Y tg ; n = У/cosτ; X 0 = X cos – Y sin ; Y 0 = Y cos + X sin

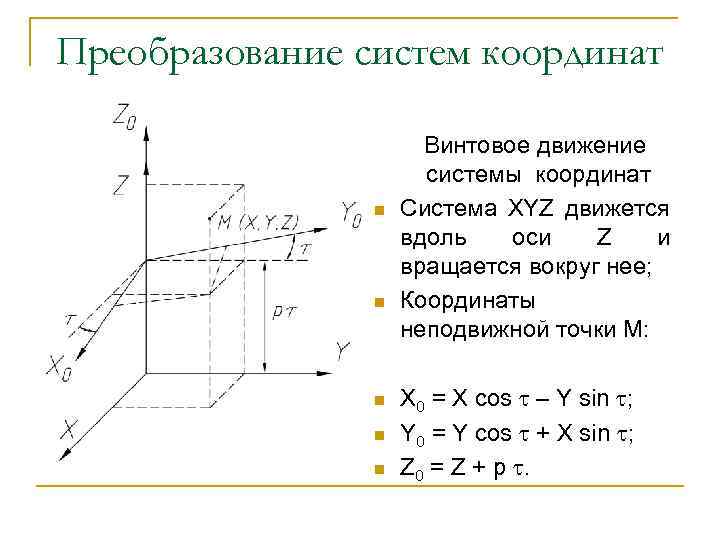Преобразование систем координат n n n Винтовое движение системы координат Система XYZ движется вдоль оси Z и вращается вокруг нее; Координаты неподвижной точки М: X 0 = X cos – Y sin ; Y 0 = Y cos + X sin ; Z 0 = Z + p .

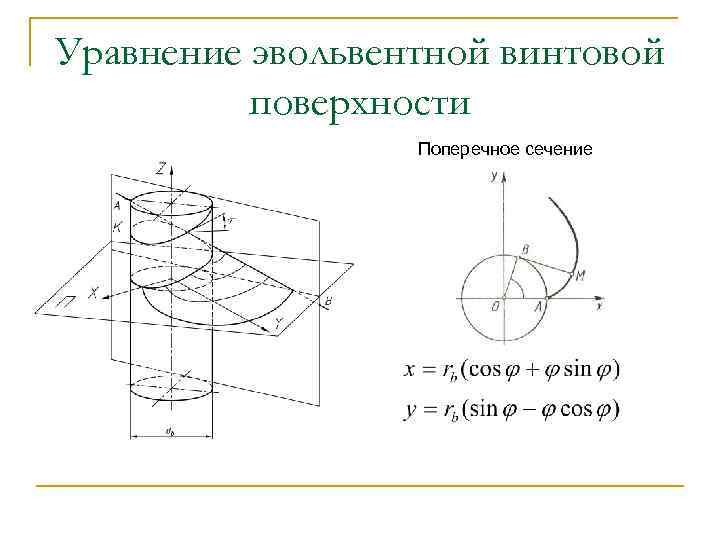Уравнение эвольвентной винтовой поверхности Поперечное сечение