
EUCLID (325 BCE - 265 BCE) • Taught geometry in Alexandria, Egypt • Put together his teacher’s theorems, wrote many of his own, and published The Elements, easily the most studied text in all of mathematics and second only to the Bible as the best selling book of all time. • Not much else is known about his life other than his work on The Elements.

The Elements: 5 postulates 1. To draw a straight line from any point to any other 2. Any straight line segment can be extended indefinitely in a straight line 3. To describe a circle with any center and distance 4. That all right angles are equal to each other 5. That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, if produced indefinitely, meet on that side on which are the angles less than the two right angles
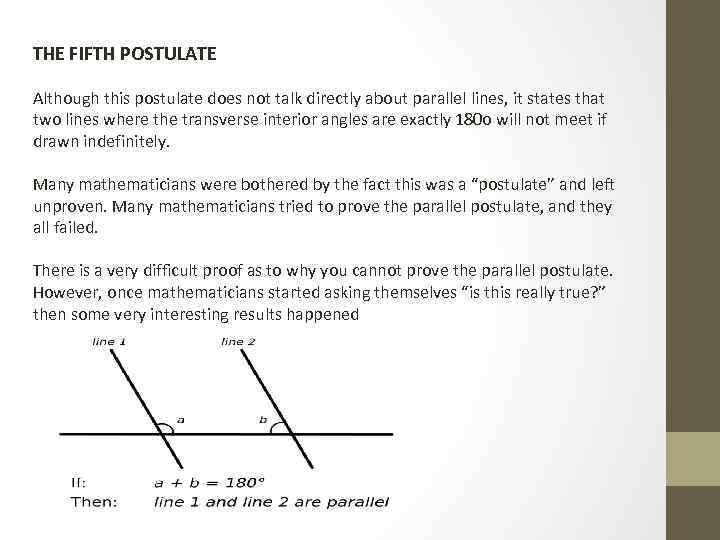
THE FIFTH POSTULATE Although this postulate does not talk directly about parallel lines, it states that two lines where the transverse interior angles are exactly 180 o will not meet if drawn indefinitely. Many mathematicians were bothered by the fact this was a “postulate” and left unproven. Many mathematicians tried to prove the parallel postulate, and they all failed. There is a very difficult proof as to why you cannot prove the parallel postulate. However, once mathematicians started asking themselves “is this really true? ” then some very interesting results happened

1792 - 1856 гг. NIKOLAI IVANOVICH LOBACHEVSKIY and his hyperbolic geometry

Lobachevskian Geometry • Roughly compared to looking down in a bowl • Changes 5 th postulate to, through a point not on a line, more than one parallel line exists • Called hyperbolic geometry because its playing field is hyperbolic • Poincare disk • Negative curvature: lines curve in opposite directions
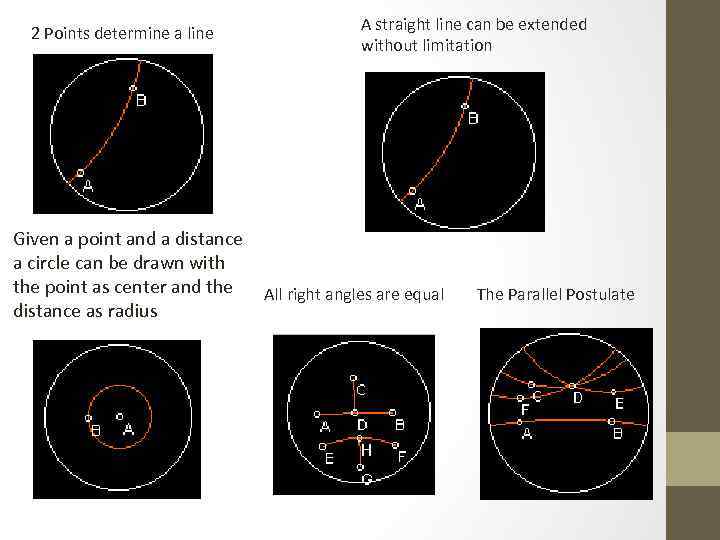
2 Points determine a line Given a point and a distance a circle can be drawn with the point as center and the distance as radius A straight line can be extended without limitation All right angles are equal The Parallel Postulate

Triangles Euclidean, Lobachevskian, Riemannian Fact: Euclidean geometry is the only geometry where two triangles can be similar but not congruent! Upon first glance, the sides do not look straight, but they are for their own surface of that geometry

C/D • Euclidean geometry, it is exactly pi • Lobachevskian, it is greater than pi • Riemannian, it is less than pi Pythagorean Theorem • Euclidean: c 2=a 2 + b 2 • Lobachevskian: c 2>a 2 + b 2 • Riemannian : c 2< a 2 + b 2

Which one is right? Poincaré added some insight to the debate between Euclidean and non. Euclidean geometries when he said, “One geometry cannot be more true than another; it can only be more convenient”. • Euclidean if you are a builder, surveyor, carpenter • Riemannian if you’re a pilot navigating the globe • Lobachevskian if you’re a theoretical physicist or plotting space travel because outer space is thought to be hyperbolic “To this interpretation of geometry, I attach great importance, for should I have not been acquainted with it, I never would have been able to develop theory of relativity. ” ~Einstein