— Это знаковая система в которой числа записываются

- Это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Позиционные СС – в которых Непозиционные СС – величина, обозначаемая цифрой в записи числа зависит от ее позиции в числе. значение цифры не зависит от ее положения в записи числа. Например: 555 Количество используемых цифр в алфавите системы счисления называется ее основанием. Например: римская СС I V X L C D M 1 5 10 50 100 500 1000 Если меньшая цифра стоит слева от большей то она вычитается, если справа - прибавляется VI = 6, IV = 4

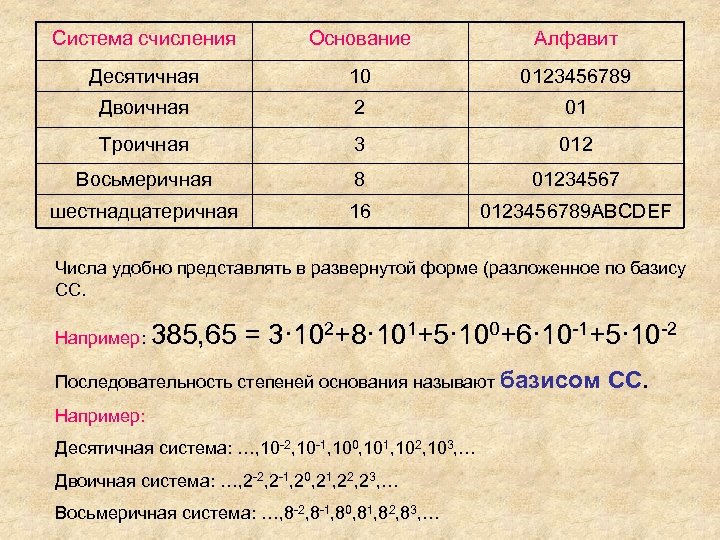Система счисления Основание Алфавит Десятичная 10 0123456789 Двоичная 2 01 Троичная 3 012 Восьмеричная 8 01234567 шестнадцатеричная 16 0123456789 ABCDEF Числа удобно представлять в развернутой форме (разложенное по базису СС. Например: 385, 65 = 3· 102+8· 101+5· 100+6· 10 -1+5· 10 -2 Последовательность степеней основания называют базисом Например: Десятичная система: …, 10 -2, 10 -1, 100, 101, 102, 103, … Двоичная система: …, 2 -2, 2 -1, 20, 21, 22, 23, … Восьмеричная система: …, 8 -2, 8 -1, 80, 81, 82, 83, … СС.

1. Какие числа записаны с помощью римских цифр MMMD, LIV, XCIX, MCMXCVII? 2. Переведите следующие числа в десятичную СС, выполните действия и запишите результат римскими цифрами? XXII-V; CV-LII; IC+XIX; MCM+VII 3. По заданному алфавиту определите основание и базис СС? а) {0, 1} б) {0, 1, 2} в) {0, 1, 2, 3} г) {0, 1, 2, 3, 4} д) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

1 способ. Представить число в развернутой форме и посчитать результат по правилам десятичной арифметики. Например: 101, 012=1· 22+0· 21+1· 20+0· 2 -1+0· 2 -2=5, 2510 2 способ (по схеме Горнера) предлагаемый способ удобен если вам необходимо составить программу перевода. Алгоритм перевода целых чисел. 1. Цифру старшего разряда умножить на основание и прибавить цифру следующего разряда 2. Полученную сумму вновь следует умножить на основание и вновь прибавить цифру следующего разряда 2078=(2· 8+0)8+7=13510; 101102=(((1· 2+0)2+1)2+0=2210 Алгоритм перевода правильных дробей. 1. Цифру младшего разряда дроби разделить на основание и прибавить цифру следующего разряда числа. 2. Полученную сумму вновь разделить на основание и вновь прибавить цифру следующего разряда. 3. В конце еще разделить на основание и к результату приписать запятую и 0.

Алгоритм перевода целого десятичного числа N в позиционную СС с основанием p. 1. Разделит нацело число N на p. 2. Полученный остаток от деления дает цифру, стоящую в нулевом разряде p-ичной записи числа N. 3. Полученное частное снова разделить нацело на p и снова запомнить полученный остаток – это цифра первого разряда и т. д. 4. Такое последовательное деление продолжается до тех пор, пока частное не станет равным 0. 5. Цифрами искомого числа являются остатки от деления, выписанные слева направо, начиная с последнего полученного остатка. Пример: 2610→X 2

Алгоритм разложения числа по базису новой СС. 1. Найти по таблице степень новой системы, ближайшую по величине к исходному числу, но не больше исходного числа – это будет первый член суммы. 2. Найти разность между исходным числом и степенью. 3. Найти по таблице степень, ближайшую к разности, - это второй член суммы. 4. Найти разность между числом, из которого выделяли степень, и степенью. 5. Так поступать, пока разность не станет равной числу, входящему в алфавит искомой системы. 6. Остается заменить полученные стерени соответствующими эквивалентами новой СС (по таблице) и подсчитать сумму, которая и есть искомое число.

Перевести число 10110 в двоичную СС Решение: Составим таблицу соответствия для двоичной и десятичной систем. Степень числа 2 Десятичное значение Двоичное значение 20 1 1 21 2 10 22 4 100 23 8 1000 24 16 10000 25 32 100000 26 64 1000000 27 128 10000000 28 256 10000 29 512 100000 210 1024 100000 Примечание: Этой таблице можно пользоваться и в обратную сторону. 10110=6410+3210+410+110=10000002+1002+12=11001012

Алгоритм перевода правильной десятичной дроби. 1. Умножить данное число на новое основание p. 2. Целая часть полученного произведения является цифрой старшего разряда искомой дроби. 3. Дробная часть полученного произведения вновь умножается на p, и целая часть результата считается следующей цифрой искомой дроби. 4. Операции продолжать до тех пор, пока дробная часть не окажется равной нулю, либо не будет достигнута требуемая точность. Пример: 0, 37510→ 0, X 2 Q=10, p=2 0, 375· 2=0, 75· 2=1, 5 0, 5· 2=1, 0

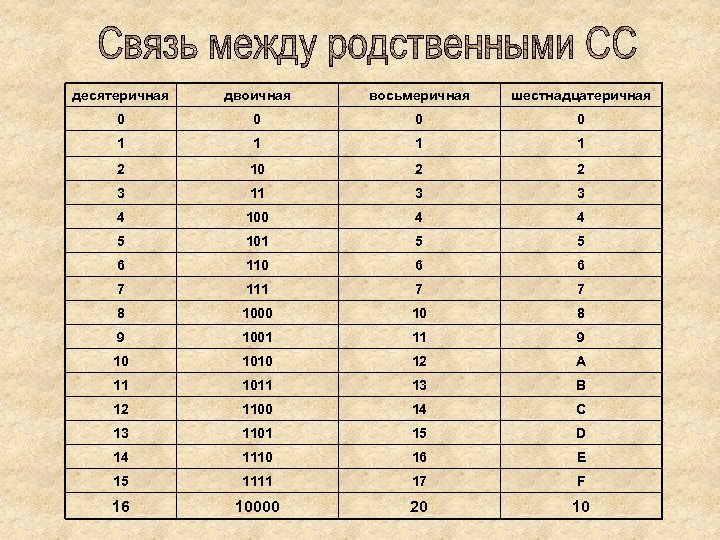десятеричная двоичная восьмеричная шестнадцатеричная 0 0 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10

Пример 1: Перевести в восьмеричную и шестнадцатеричную СС число 1011000010, 00110012 Решение: 001 011 000 010 , 001 100 - двоичное число 1 3 0 2 , 1 4 4 - восьмеричное число Разобьем число по 4 цифры 0010 1100 0010 , 0011 0010 - двоичное число 2 С 2 , 3 2 - шестнадцатеричное число Результат: 1011000010, 00110012=1302, 1448=2 С 2, 3216

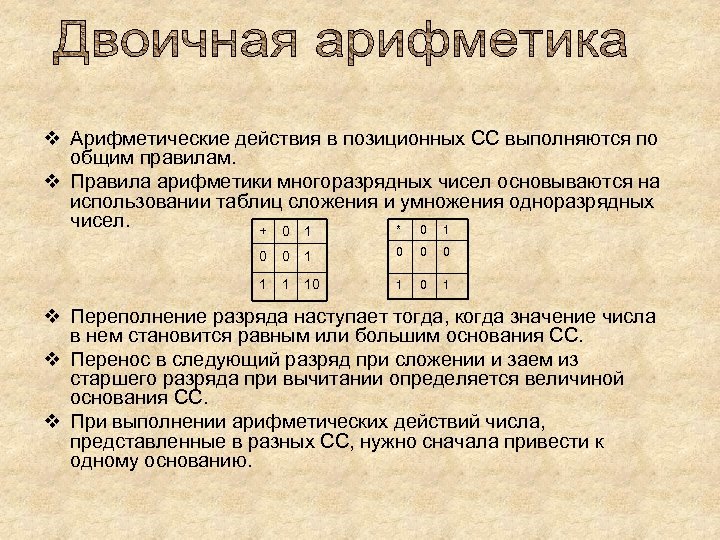v Арифметические действия в позиционных СС выполняются по общим правилам. v Правила арифметики многоразрядных чисел основываются на использовании таблиц сложения и умножения одноразрядных чисел. * 0 1 + 0 1 0 0 0 1 1 10 1 v Переполнение разряда наступает тогда, когда значение числа в нем становится равным или большим основания СС. v Перенос в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания СС. v При выполнении арифметических действий числа, представленные в разных СС, нужно сначала привести к одному основанию.

Пример: + 1102 * 112 10012 112 + 1102 110 100102