GLAVA_1_ch_3_matematicheskie_modeli.ppt
- Количество слайдов: 24
 Этапы моделирования ØПостановка задачи. ØПостроение модели. На этом этапе формулируются законы, связывающие составные части модели. ØОтыскание решения. Построение алгоритма, моделирующего поведение объекта. ØКонтроль правильности результатов и их внедрение. ØСовершенствование модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 1
Этапы моделирования ØПостановка задачи. ØПостроение модели. На этом этапе формулируются законы, связывающие составные части модели. ØОтыскание решения. Построение алгоритма, моделирующего поведение объекта. ØКонтроль правильности результатов и их внедрение. ØСовершенствование модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 1
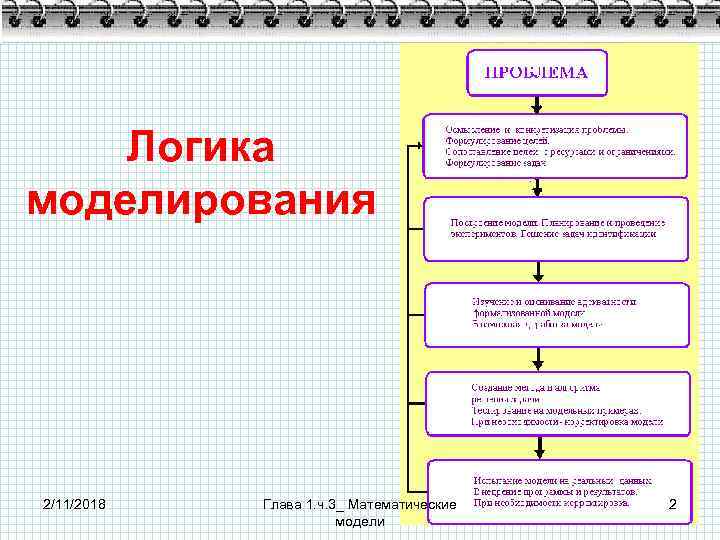 Логика моделирования 2/11/2018 Глава 1. ч. 3_ Математические модели 2
Логика моделирования 2/11/2018 Глава 1. ч. 3_ Математические модели 2
 2/11/2018 Глава 1. ч. 3_ Математические модели 3
2/11/2018 Глава 1. ч. 3_ Математические модели 3
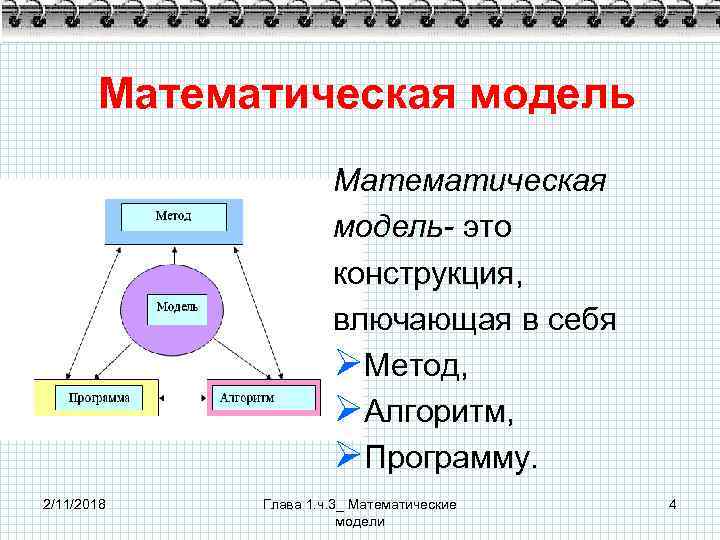 Математическая модель- это конструкция, влючающая в себя ØМетод, ØАлгоритм, ØПрограмму. 2/11/2018 Глава 1. ч. 3_ Математические модели 4
Математическая модель- это конструкция, влючающая в себя ØМетод, ØАлгоритм, ØПрограмму. 2/11/2018 Глава 1. ч. 3_ Математические модели 4
 Математическая модель 2/11/2018 Глава 1. ч. 3_ Математические модели 5
Математическая модель 2/11/2018 Глава 1. ч. 3_ Математические модели 5
 Математическая модель 1. 2. 4. Классификация математических моделей. Математические модели как проекции реальных объектов характеризуются рядом особенностей, в зависимости от которых можно их классифицировать. 2/11/2018 Глава 1. ч. 3_ Математические модели 6
Математическая модель 1. 2. 4. Классификация математических моделей. Математические модели как проекции реальных объектов характеризуются рядом особенностей, в зависимости от которых можно их классифицировать. 2/11/2018 Глава 1. ч. 3_ Математические модели 6
 Математическая модель 1. Модель называется изоморфной (одинаковой по форме), если между нею и реальной системой существует полное поэлементное соответствие, и гомоморфной, если существует соответствие лишь между наиболее значительными составными частями объекта и модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 7
Математическая модель 1. Модель называется изоморфной (одинаковой по форме), если между нею и реальной системой существует полное поэлементное соответствие, и гомоморфной, если существует соответствие лишь между наиболее значительными составными частями объекта и модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 7
 Математическая модель 2. По принципам построения и способам получения решения модели разделяют на аналитические и имитационные. Аналитические модели позволяют получить явные функциональные зависимости для искомых величин или определить численные решения для конкретных начальных условий и количественные характеристики модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 8
Математическая модель 2. По принципам построения и способам получения решения модели разделяют на аналитические и имитационные. Аналитические модели позволяют получить явные функциональные зависимости для искомых величин или определить численные решения для конкретных начальных условий и количественные характеристики модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 8
 Математическая модель Если модели исключают возможность аналитического решения, то модель следует изучать с помощью имитационного моделирования, то есть многократного испытания модели с различными наборами входных данных, для того чтобы определить их влияние на выходные критерии оценки работы системы. 2/11/2018 Глава 1. ч. 3_ Математические модели 9
Математическая модель Если модели исключают возможность аналитического решения, то модель следует изучать с помощью имитационного моделирования, то есть многократного испытания модели с различными наборами входных данных, для того чтобы определить их влияние на выходные критерии оценки работы системы. 2/11/2018 Глава 1. ч. 3_ Математические модели 9
 Математическая модель 3. Особенности функционирования объектов моделирования и вид используемого математического описания определяют непрерывный или дискретный характер модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 10
Математическая модель 3. Особенности функционирования объектов моделирования и вид используемого математического описания определяют непрерывный или дискретный характер модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 10
 Математическая модель 4. Если математическая модель в качестве одной из основных характеристик включает время, то модель называют динамической, если время не включено, - стационарной. 2/11/2018 Глава 1. ч. 3_ Математические модели 11
Математическая модель 4. Если математическая модель в качестве одной из основных характеристик включает время, то модель называют динамической, если время не включено, - стационарной. 2/11/2018 Глава 1. ч. 3_ Математические модели 11
 Математическая модель 5. Цели проектирования определяют детерминированный или стохастический (вероятностно-статистический) подход к построению модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 12
Математическая модель 5. Цели проектирования определяют детерминированный или стохастический (вероятностно-статистический) подход к построению модели. 2/11/2018 Глава 1. ч. 3_ Математические модели 12
 Математическая модель 1. 2. 5. Примеры простейших математических моделей 2/11/2018 Глава 1. ч. 3_ Математические модели 13
Математическая модель 1. 2. 5. Примеры простейших математических моделей 2/11/2018 Глава 1. ч. 3_ Математические модели 13
 Математическая модель При построении математических моделей используют Øфундаментальные законы природы, Øвариационные принципы, Øаналогии и Øиерархические подходы: сверху- вниз и снизу- вверх, Øа также данные экспериментальных исследований. 2/11/2018 Глава 1. ч. 3_ Математические модели 14
Математическая модель При построении математических моделей используют Øфундаментальные законы природы, Øвариационные принципы, Øаналогии и Øиерархические подходы: сверху- вниз и снизу- вверх, Øа также данные экспериментальных исследований. 2/11/2018 Глава 1. ч. 3_ Математические модели 14
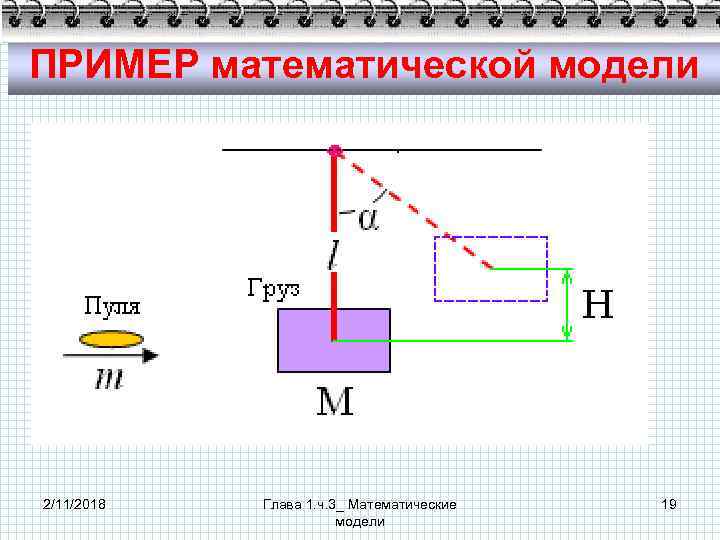
 ПРИМЕР математической модели Пуля попадает в груз, подвешенный на легком, жестком и свободно вращающемся стержне. Пуля застревает в грузе и сообщает системе груз+пуля свою кинетическую энергию. Составить ММ системы. 2/11/2018 Глава 1. ч. 3_ Математические модели 15
ПРИМЕР математической модели Пуля попадает в груз, подвешенный на легком, жестком и свободно вращающемся стержне. Пуля застревает в грузе и сообщает системе груз+пуля свою кинетическую энергию. Составить ММ системы. 2/11/2018 Глава 1. ч. 3_ Математические модели 15
 ПРИМЕР математической модели Цели: изучение механического взаимодействия груза и пули. Задачи: ØВычисление угла отклонения груза, при известных массе груза, массе пули и скорости полета пули. ØВычисление скорости полета пули при известных массах и угле отклонения. ØВычисление массы груза при известных скорости и массы пули, а также угла отклонения. ØИ др. 2/11/2018 Глава 1. ч. 3_ Математические модели 16
ПРИМЕР математической модели Цели: изучение механического взаимодействия груза и пули. Задачи: ØВычисление угла отклонения груза, при известных массе груза, массе пули и скорости полета пули. ØВычисление скорости полета пули при известных массах и угле отклонения. ØВычисление массы груза при известных скорости и массы пули, а также угла отклонения. ØИ др. 2/11/2018 Глава 1. ч. 3_ Математические модели 16
 ПРИМЕР математической модели Условия и ограничения: ØСтержень несжимаемый и невесомый. ØПотери энергии на разгон стержня и нагрев пули и груза незначительны. 2/11/2018 Глава 1. ч. 3_ Математические модели 17
ПРИМЕР математической модели Условия и ограничения: ØСтержень несжимаемый и невесомый. ØПотери энергии на разгон стержня и нагрев пули и груза незначительны. 2/11/2018 Глава 1. ч. 3_ Математические модели 17
 ПРИМЕР математической модели Учитывая сформулированные ограничения и условия воспользуемся законом сохранения механической энергии: Кинетическая энергия пули равна кинетической энергии системы пуля+груз+стержень и полностью переходит в потенциальную энергию системы. 2/11/2018 Глава 1. ч. 3_ Математические модели 18
ПРИМЕР математической модели Учитывая сформулированные ограничения и условия воспользуемся законом сохранения механической энергии: Кинетическая энергия пули равна кинетической энергии системы пуля+груз+стержень и полностью переходит в потенциальную энергию системы. 2/11/2018 Глава 1. ч. 3_ Математические модели 18
 ПРИМЕР математической модели 2/11/2018 Глава 1. ч. 3_ Математические модели 19
ПРИМЕР математической модели 2/11/2018 Глава 1. ч. 3_ Математические модели 19
 ПРИМЕР математической модели 2/11/2018 Глава 1. ч. 3_ Математические модели 20
ПРИМЕР математической модели 2/11/2018 Глава 1. ч. 3_ Математические модели 20
 ПРИМЕР математической модели 2/11/2018 Глава 1. ч. 3_ Математические модели 21
ПРИМЕР математической модели 2/11/2018 Глава 1. ч. 3_ Математические модели 21
 ПРИМЕР математической модели 2/11/2018 Глава 1. ч. 3_ Математические модели 22
ПРИМЕР математической модели 2/11/2018 Глава 1. ч. 3_ Математические модели 22
 ПРИМЕР математической модели Построена Øгомеоморфная, Øстационарная, Øаналитическая, Øдискретная, Øдетерминированная модель. 2/11/2018 Глава 1. ч. 3_ Математические модели 23
ПРИМЕР математической модели Построена Øгомеоморфная, Øстационарная, Øаналитическая, Øдискретная, Øдетерминированная модель. 2/11/2018 Глава 1. ч. 3_ Математические модели 23
 2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ 2. 1. Эксперимент и идентификация модели 2/11/2018 Глава 1. ч. 3_ Математические модели 24
2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ 2. 1. Эксперимент и идентификация модели 2/11/2018 Глава 1. ч. 3_ Математические модели 24


