Если продолжить одно из маленьких звеньев ломаной

«Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то эта продолженная таким образом сторона будет называться касательной к кривой. »

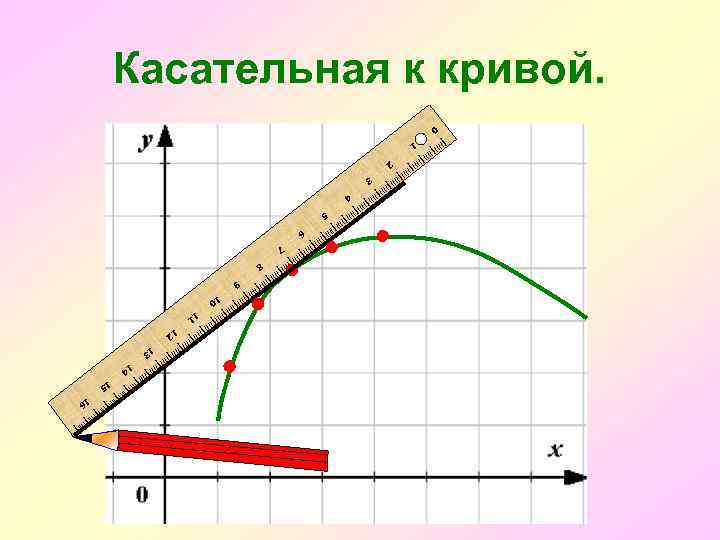Касательная к кривой. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 I I III I I I II III I III I II III IIIII III I II III III IIII II I II II IIIII III IIII II IIIII I

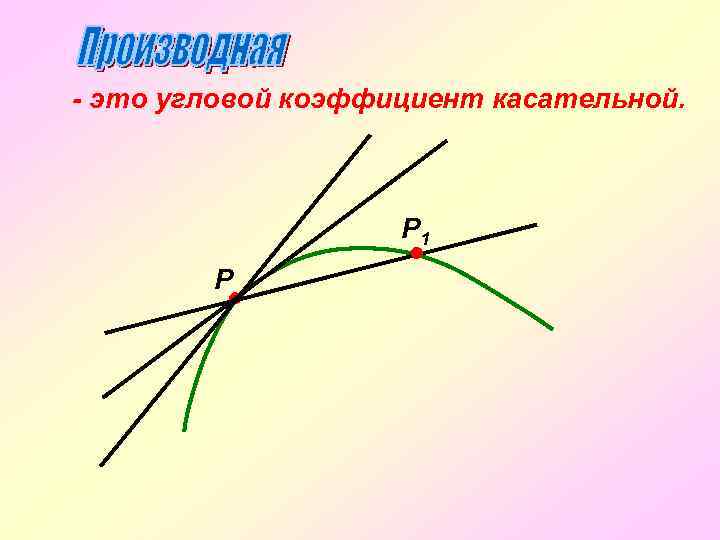- это угловой коэффициент касательной. Р 1 Р

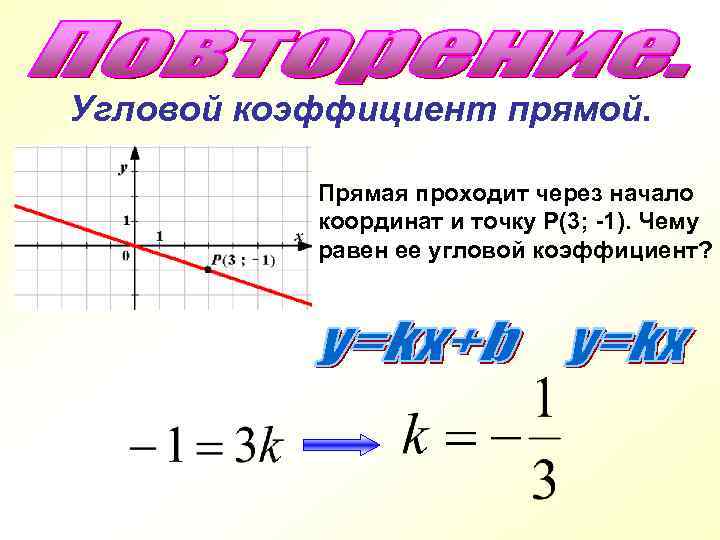Угловой коэффициент прямой. Прямая проходит через начало координат и точку Р(3; -1). Чему равен ее угловой коэффициент?

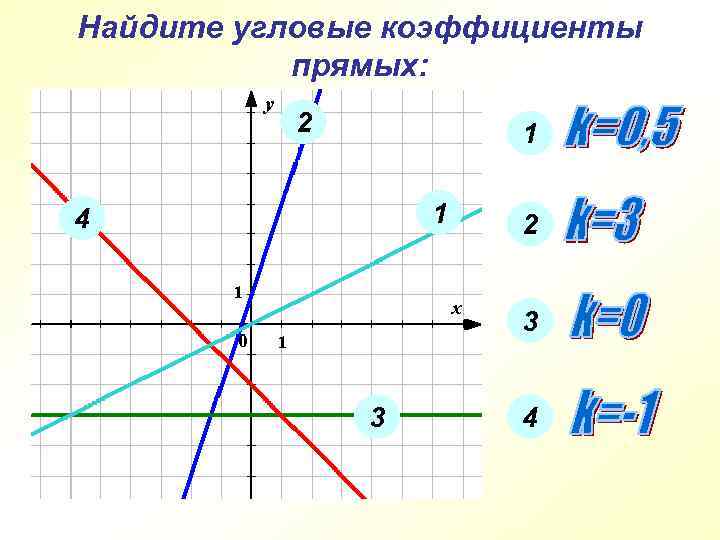Найдите угловые коэффициенты прямых: 2 1 1 4 2 3 3 4

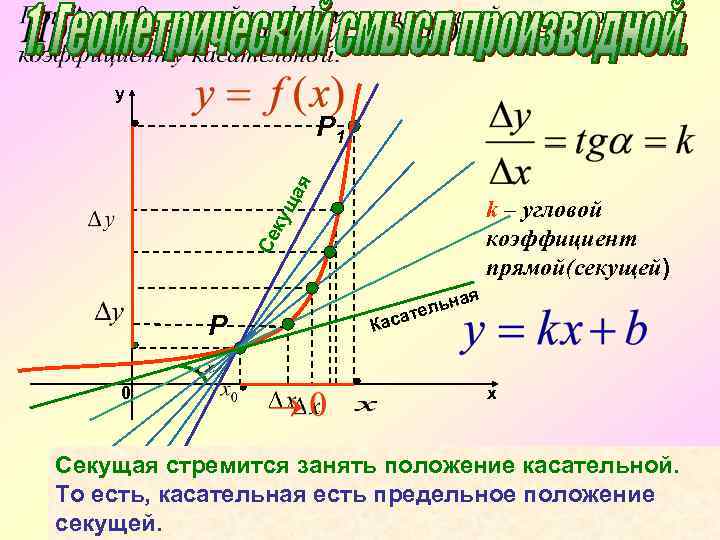y ая Р 1 Се к ущ k – угловой коэффициент прямой(секущей) Р 0 ая льн е асат К х Секущая стремится занять положение касательной. То есть, касательная есть предельное положение секущей.

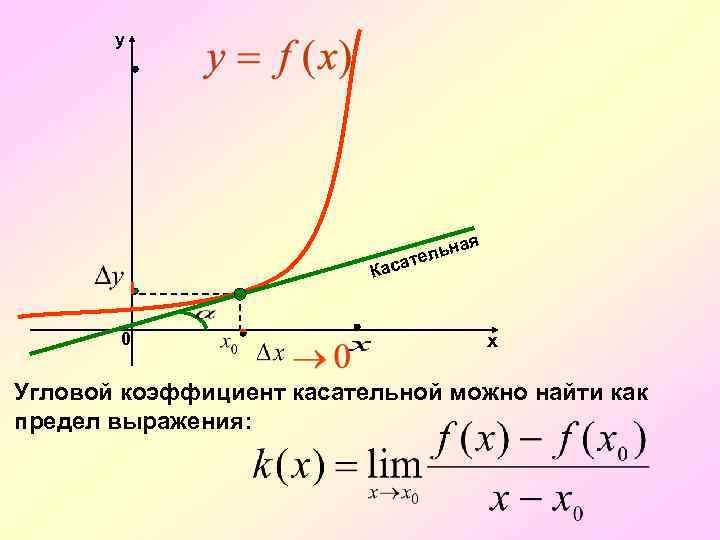y я ьна ател Кас 0 х Угловой коэффициент касательной можно найти как предел выражения:

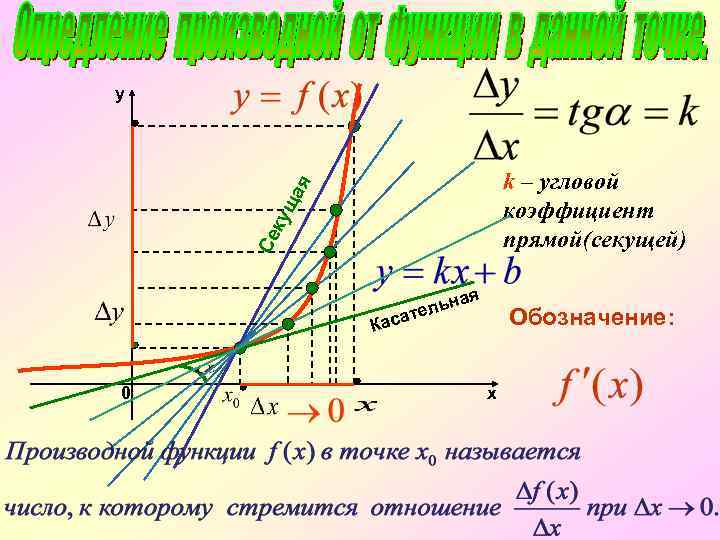y Се к ущ ая k – угловой коэффициент прямой(секущей) ая льн ате Обозначение: Кас 0 х

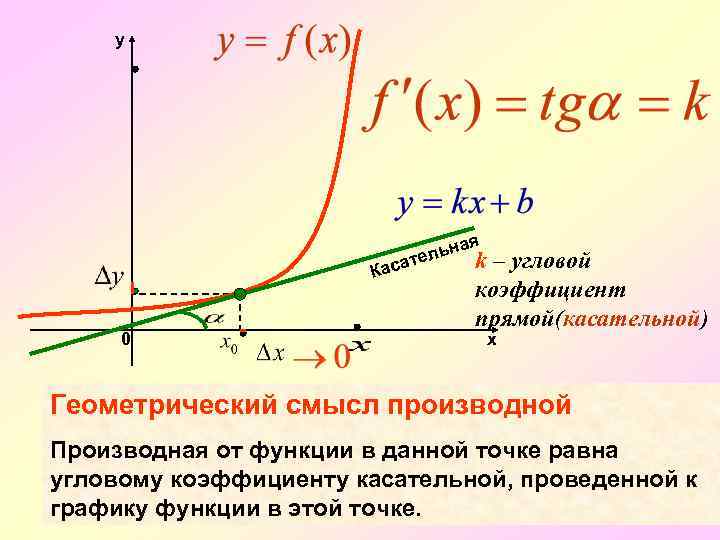y я ьна k ател Кас 0 – угловой коэффициент прямой(касательной) х Геометрический смысл производной Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

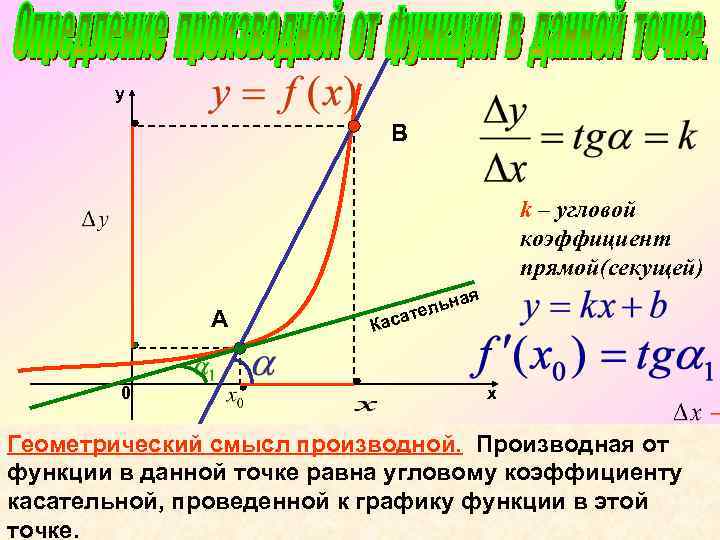y В k – угловой коэффициент прямой(секущей) А 0 ая льн ате Кас х Геометрический смысл производной. Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Исаак Ньютон (1643 – 1727) «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад. »

Свободное падение t t 1

Свободное падение t t 1

Используя слово «предел» , можно сказать, что мгновенная скорость в точке t – это предел средней скорости при стягивании отрезка, на котором она изменяется, в точку t или в символической записи - это скорость

Δх – перемещение тела Δt – промежуток времени в течение которого выполнялось движение .