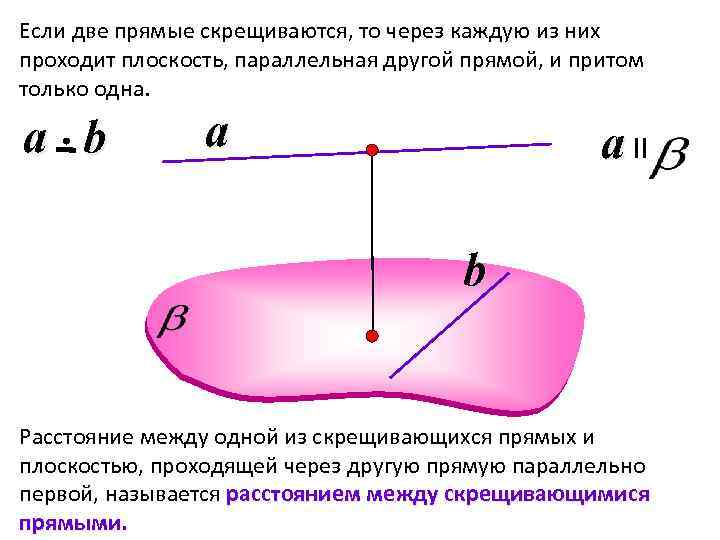
Если две прямые скрещиваются то через каждую из

Если две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна. a b a a II b Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

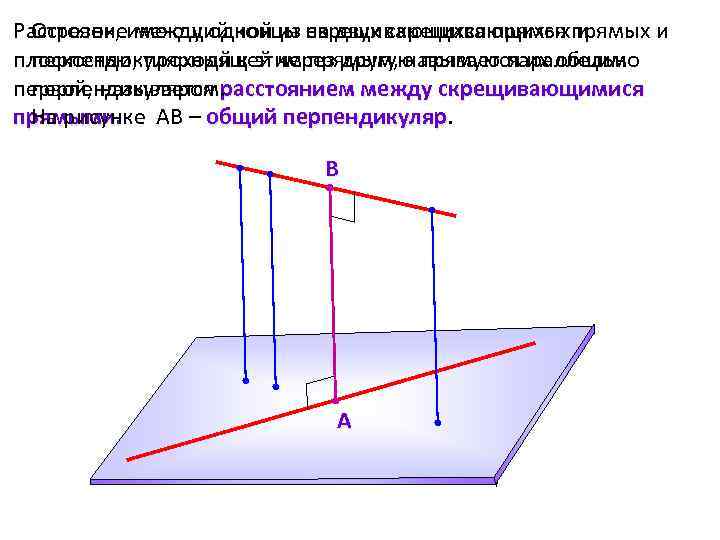Расстояниеимеющий концы на двух скрещивающихся прямых и Отрезок, между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно перпендикулярный к этим прямым, называется их общим первой, называется расстоянием между скрещивающимися перпендикуляром. прямыми. АВ – общий перпендикуляр. На рисунке перпендикуляр В А

Повторение. Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной. А П-Р Н Н-я П-я a М

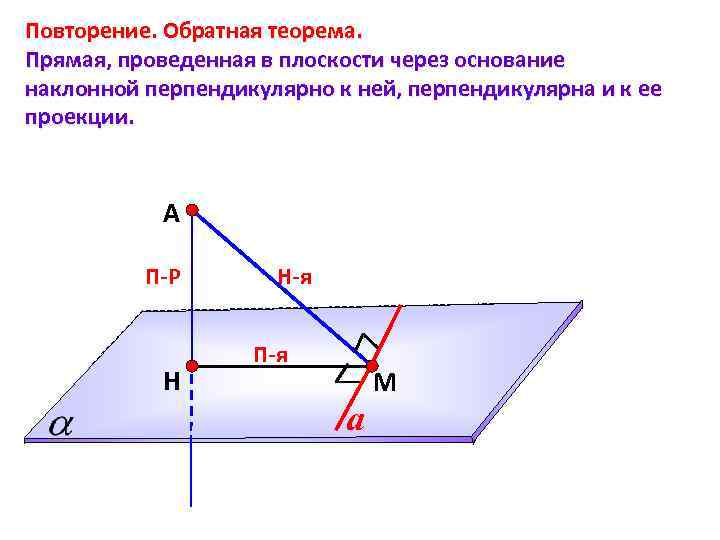Повторение. Обратная теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции. А П-Р Н Н-я П-я a М

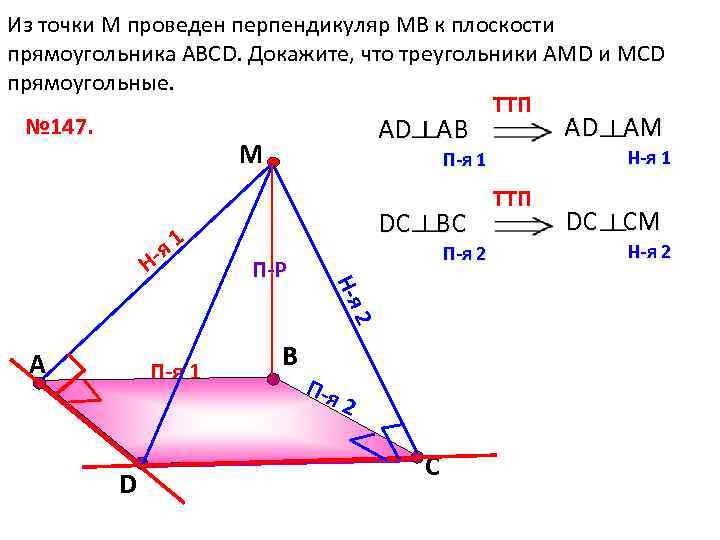Из точки М проведен перпендикуляр МВ к плоскости прямоугольника АВСD. Докажите, что треугольники АМD и МСD прямоугольные. TTП № 147. AD AM AD AB М я 1 - Н П-я 1 D DC BC П-Р В П-я 2 2 Н-я А Н-я 1 П-я 2 С TTП DC CM Н-я 2

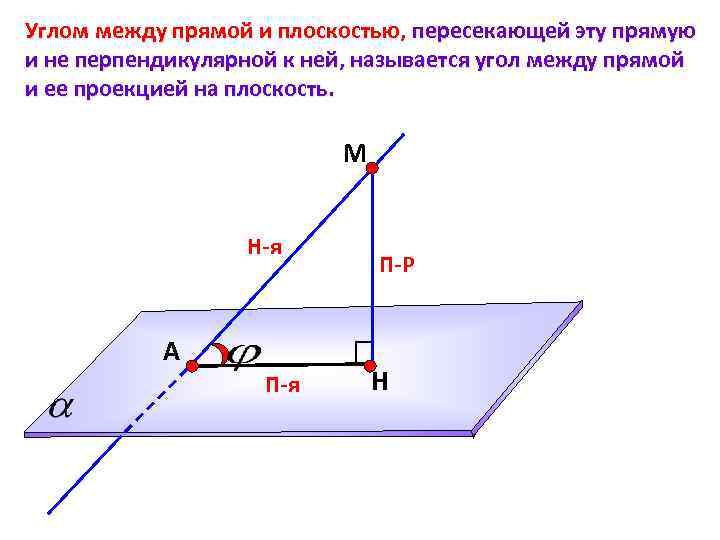Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость. М Н-я А П-я П-Р Н

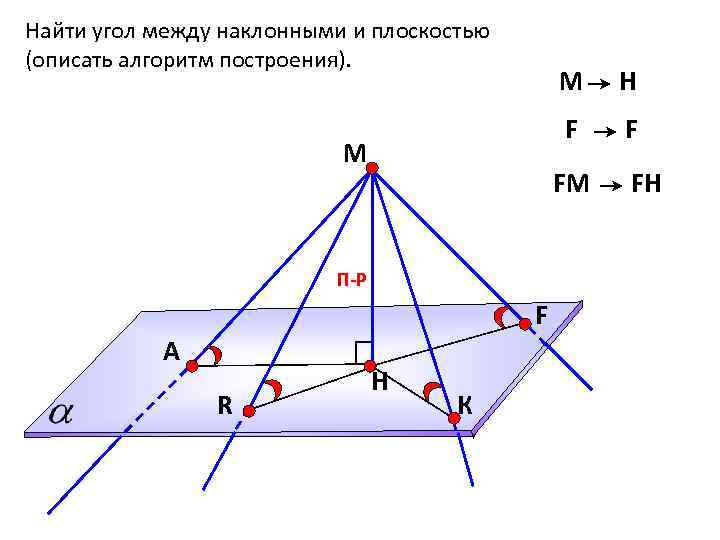Найти угол между наклонными и плоскостью (описать алгоритм построения). М F R F FМ П-Р А H Н К FH

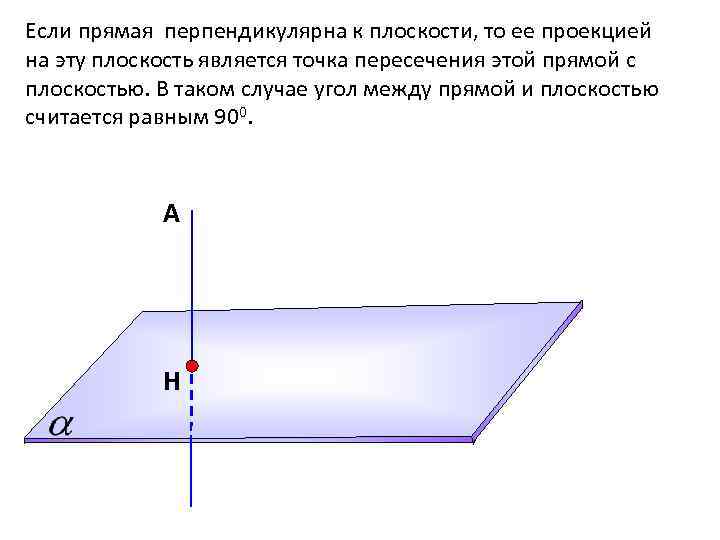Если прямая перпендикулярна к плоскости, то ее проекцией на эту плоскость является точка пересечения этой прямой с плоскостью. В таком случае угол между прямой и плоскостью считается равным 900. А Н

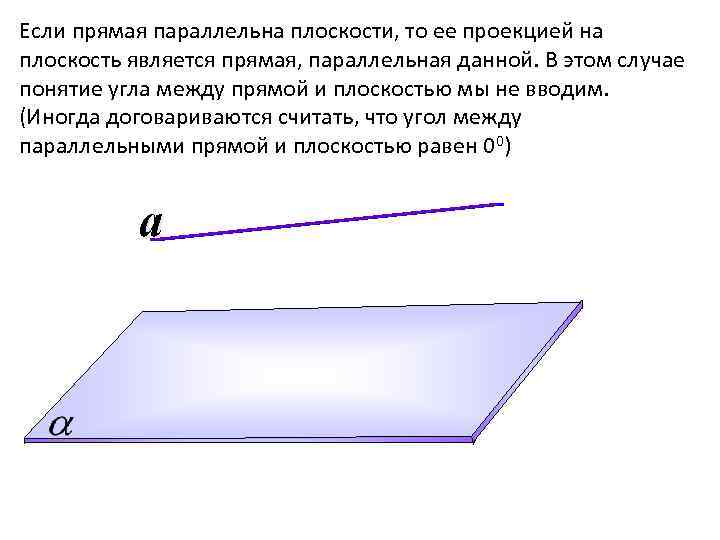Если прямая параллельна плоскости, то ее проекцией на плоскость является прямая, параллельная данной. В этом случае понятие угла между прямой и плоскостью мы не вводим. (Иногда договариваются считать, что угол между параллельными прямой и плоскостью равен 00) a

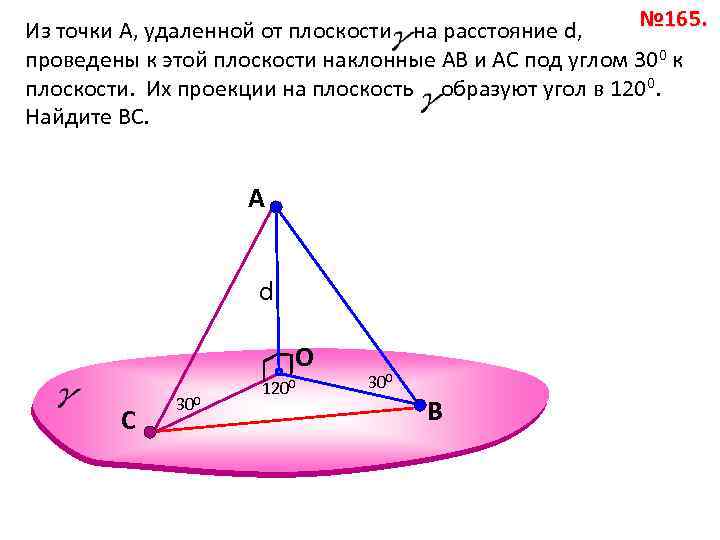№ 165. Из точки А, удаленной от плоскости на расстояние d, проведены к этой плоскости наклонные АВ и АС под углом 300 к плоскости. Их проекции на плоскость образуют угол в 1200. Найдите ВС. A d O С 300 1200 300 В

ДОМАШНЕЕ ЗАДАНИЕ 1. № 162 оформить в тетрадь 2. № 163; 164 Дополнительная задача (на доп. оценку): Найдите периметр прямоугольного треугольника, если радиус вписанной окружности равен 1, а радиус описанной окружности равен 2, 5. Напоминание: 1. Длина отрезков касательных, проведенных из одной точки до точки касания, равны. 2. Гипотенуза вписанного прямоугольного треугольника является диаметром окружности. К О