Еще раз об элементарной статистике n. Теоретические


Еще раз об элементарной статистике n. Теоретические распределения n. Эмпирическое распределение n. Критерии согласия n. Вероятность n. Теория выборок n. Доверительный интервал n. Оценка значимости

ПРЕДИСЛОВИЕ Термин «статистика» происходит от латинского слова статус (status), что означает определенное положение вещей. Первоначально он употреблялся в значении слова государство ведение и был введен в обиход в 1749 г. немецким ученым Г. Ахенвалем выпустившим книгу о государствоведении. В настоящее время термин статистика употребляется в 3 значениях: n как отрасль практической деятельности людей направленную на сбор обработку анализ данных n как наука, занимающаяся разработкой технических положений и методов используемых статистической практикой n как статистические данные, представленные в отчетности или данные публикуемые в сборниках справочниках периодической прессе которые представляют собой результат статистической работы.
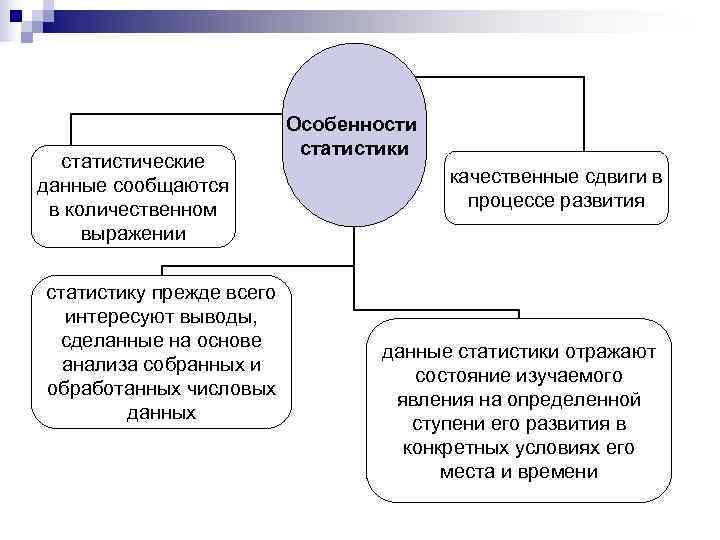
Особенности статистики статистические данные сообщаются качественные сдвиги в в количественном процессе развития выражении статистику прежде всего интересуют выводы, сделанные на основе данные статистики отражают анализа собранных и состояние изучаемого обработанных числовых явления на определенной данных ступени его развития в конкретных условиях его места и времени

История развития статистики в Х-ХIV веках Статистика имеет многовековую историю и своими корнями уходит в глубокую древность. С образованием государств появилась необходимость в статистической практике, т. е. в сборе сведений о наличии земель, численности населения, о его имущественном положении. Несколько тысячелетий назад такой учёт проводился в Китае, Древнем Риме и в Египте. На Руси уже в Х-ХII веках собирались различного рода сведения связанные с налогообложением.

Статистика как наука стала развиваться с середины ХVII века по двум направлениям • описательному • математическому

Важнейшими представителями описательной школы государство ведения были немецкие ученые Г. Конринг (1606 - 1681) и Г. Ахенваль (1719 -1772). Задачей статистики его представители считали описание государственных достопримечательностей, к числу которых относили n • территорию государства n • государственное устройство n • население n • религию внешнюю политику и т. п. Вторая особенность описательного направления статистики — в этих работах отсутствовал анализ закономерностей и взаимосвязей исследуемых явлений и процессов.

Математическое направление зародилось в Англии В отличие от описательной школы представители математического направления (политической арифметики) ставили своей задачей выявление закономерностей и взаимосвязей явлений с помощью различных расчетов. Свои выводы они основывали на числовых данных. Виднейшим представителем этого направления был У. Петти (1623 -1687). В дальнейшем это направление значительно развилось в работах Ф. Гальтона (1822 - 1911), К. Пирсона (1857 - 1936), В. Госсета (1876 - 1936), Р. Фишера (1890 - 1962) и др.

В настоящее время статистика имеет следующее определение. Статистика - это планомерный и систематический учет массовых общественных явлений, который осуществляется государственными статистическими органами и дает числовое выражение проявляющимся закономерностям. Вообще статистик очень много, например: статистика промышленности, статистика торговли, экономическая статистика, математическая, прикладная и т. д. Так как статистика имеет дело с массовыми явлениями, то основным понятием является статистическая совокупность.

Статистическая совокупность - это множество объектов или явлений, изучаемых статистикой, которые имеют один или несколько общих признаков и различаются между собой по другим признакам. Отдельные объекты или явления, образующие статистическую совокупность, называются единицами совокупности. Статистический показатель - это количественная оценка свойства изучаемого явления. Признак - это характерное свойство изучаемого явления, отличающее его от других явлений. Таким образом, статистических признаков, т. е. свойств, качеств объектов наблюдения очень много. Все их многообразие принято делить на две большие группы: признаки качества и признаки количества. Качественный признак (атрибутивный) - признак, отдельные значения которого выражаются в виде понятий, наименований. Ясно, пасмурно… Количественный признак - признак, определенные значения которого имеют количественные выражения. Рост - 185, 172, 164, 158. Вес - 105, 72, 54, 48.

Вариация - это многообразие, изменяемость величины признака у отдельных единиц совокупности наблюдения. Вариация признака - пол - мужской, женский. Вариация з/п - 10000, 1000000. Отдельные значения признака называются вариантами этого признака.

Теоретические распределения n Биномиальное n Муавра-Гаусса-Лапласа (нормальное) n Пуассона
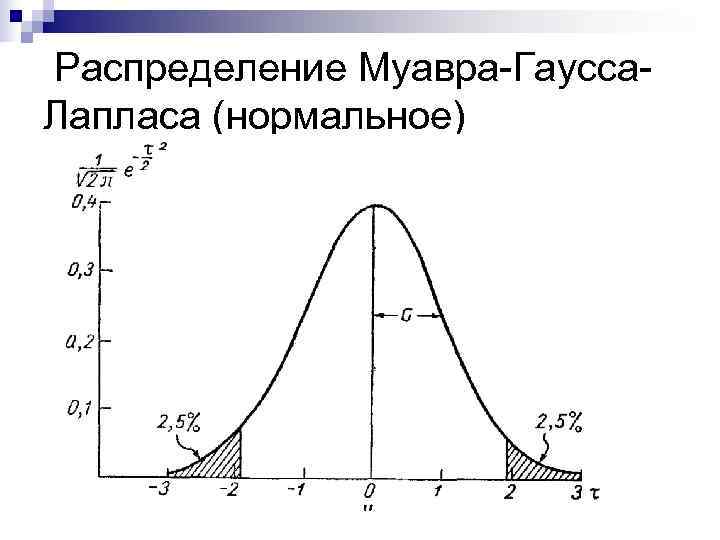
Распределение Муавра-Гаусса- Лапласа (нормальное)
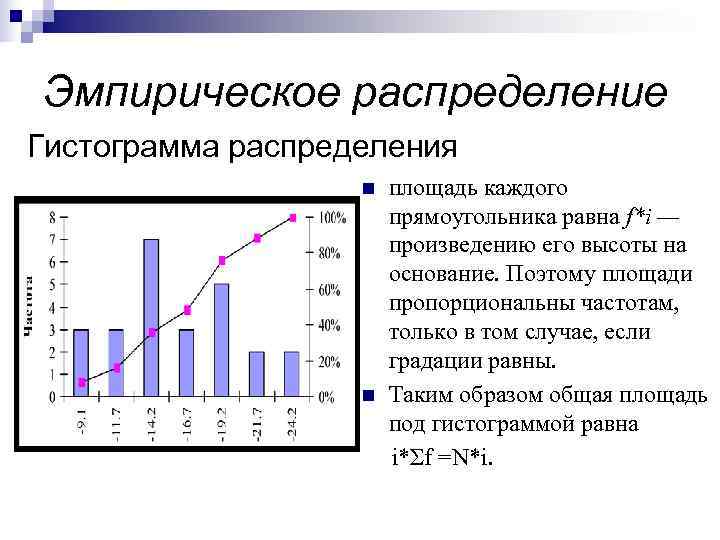
Эмпирическое распределение Гистограмма распределения n площадь каждого прямоугольника равна f*i — произведению его высоты на основание. Поэтому площади пропорциональны частотам, только в том случае, если градации равны. n Таким образом общая площадь под гистограммой равна i*Σf =N*i.

Интегральная кривая n В статистике величинам случайной переменной ниже которых лежат определенные части общего числа наблюдений присвоены специальные наименования. n Величина ниже которой лежит k% случаев называется k-той прецентилью. n (Прецентиль - сотая часть). Величина ниже которой j/30 наблюдений называется трентиль (трентиль — тридцатая часть). Подобным же образом n квартили относятся к четвертой n квантили к пятой n децили к десятой частям. Некоторые исследователи используют эти термины для обозначения не точек кривой, а просто некоторых частей общего числа наблюдений.

Связь распределения повторяемостей с вероятностью n Если f —частота отдельного события, а N - число всех событий, то отношение f/N - называется вероятностью этого события. Вероятность может быть выражена дробью или в процентах Ясно, что она не может превышать 1 (100%) или быть меньше 0.
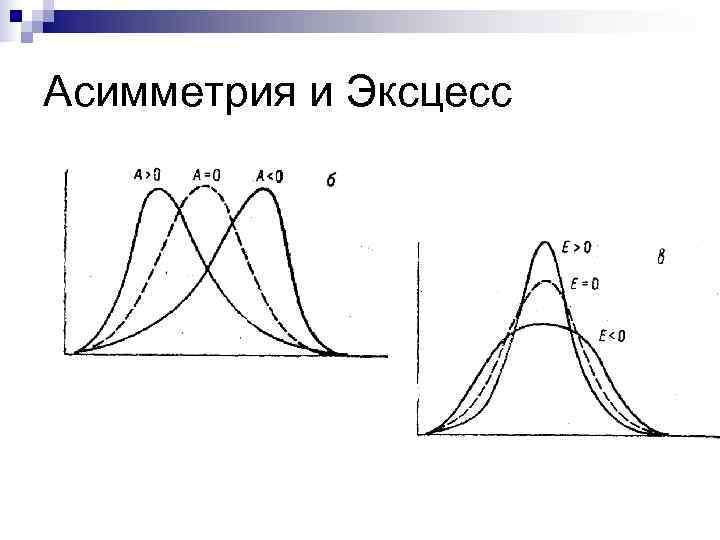
Асимметрия и Эксцесс

Сравнение по характеру распределения n Анализируя форму распределения, исследователь обычно оценивает степень соответствия исходного эмпирического вариационного ряда предполагаемому теоретическому (модельному) распределению. В некоторых случаях по форме распределения сравниваются между собой выборки, причем оцениваются гипотезы о принадлежности этих выборок к совокупностям с одинаковым или разным (не определяя каким именно) характером распределения. В обоих вариантах задача сводится к оценке различий двух эмпирических или эмпирической и теоретической рядов частот. Наиболее распространены два метода – метод хи-квадрат и метод Колмогорова-Смирнова. n Метод «хи-квадрат» . Критерий χ2 предложен Пирсоном, и оценивает разности частот. Критерий λ Колмогорова— Смирнова основан на сравнении рядов накопленных частот. Предполагается, что распределение исследуемой величины выражено некоторой непрерывной функцией.

Выборочные характеристики, полученные на первом этапе статистического исследования должны быть соответствующим образом оценены. При этом могут возникнуть следующие задачи: n определение степени соответствия выборочных показателей истинным параметрам генеральной совокупности; n установление принадлежности отдельного значения варианты к выборке генеральной совокупности; n сравнение выборок - а) по сводным показателям б) по общему характеру распределения.
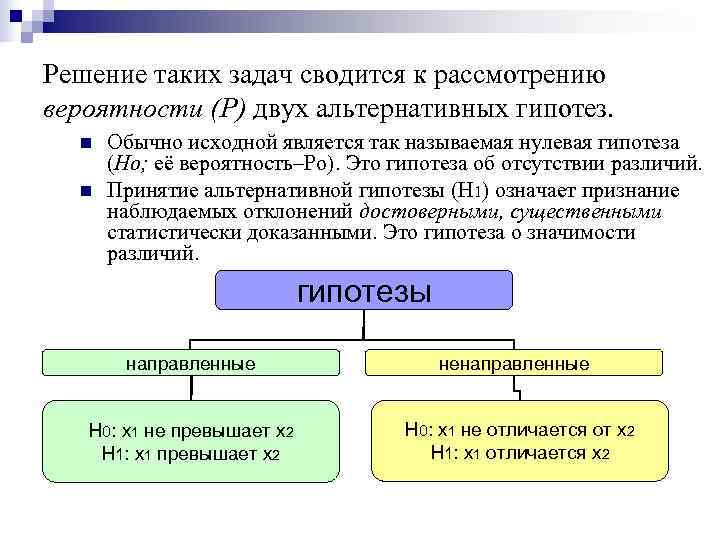
Решение таких задач сводится к рассмотрению вероятности (Р) двух альтернативных гипотез. n Обычно исходной является так называемая нулевая гипотеза (Но; её вероятность–Ро). Это гипотеза об отсутствии различий. n Принятие альтернативной гипотезы (Н 1) означает признание наблюдаемых отклонений достоверными, существенными статистически доказанными. Это гипотеза о значимости различий. гипотезы направленные ненаправленные Н 0: х1 не превышает х2 Н 0: х1 не отличается от х2 Н 1: х1 превышает х2 Н 1: х1 отличается х2

Условно выбраны 3 основных доверительных уровня при которых принимается или отвергается Но: n I уровень Ро < 0. 05; II уровень Ро<0, 01; III уровень Ро< 0, 001. n При соблюдении этого условия Но отвергается и чем выше доверительный уровень на котором делается вывод тем больше уверенность в его обоснованности (Р 1=1–Р 0 — значимость вывода).

Доверительные интервалы Любая выборочная характеристика (выборочная статистика) полученная по данным одной выборки является отдельной случайно величиной из распределения множества таких же случайных величин. Значение соответствующего показателя в генеральной совокупности (генеральный параметр) находится в центре такого распределения. Имея множество независимых выборок из одной генеральной совокупности, мы могли бы получить достаточно точную величину генерального параметра. Однако и по отдельной выборке можно с определенной вероятностью найти область его возможных значений — доверительный интервал.

Определение границ доверительного интервала для тех выборочных статистик которые подчиняются законам нормального распределения, в общем виде такое генеральный параметр, соответствующая выборочная статистика и ее стандартная ошибка, иα- некоторый коэффициент при α = Ро. Для малых выборок иα заменяется значением коэффициента Стьюдента tα, υ при υ =N – 1. Для больших выборок иα=0, 05=1, 96, иα=0, 01=2, 58 и иα=0, 001=3, 29. Такое определение доверительного интервала применяется для х и в случае N >30(20) или при N <30, но нормальном распределении.

Случайное варьирование выборочной статистики (не следует путать с систематическими ошибками – ошибками измерений) измеряется ее стандартной ошибкой (sk или тk) где индекс — обозначение соответствующей статистики которая тем больше чем более изменчивы значения исследуемого признака в генеральной совокупности и чем меньше объем выборки. Формулы стандартных ошибок основных выборочных статистик следующие:
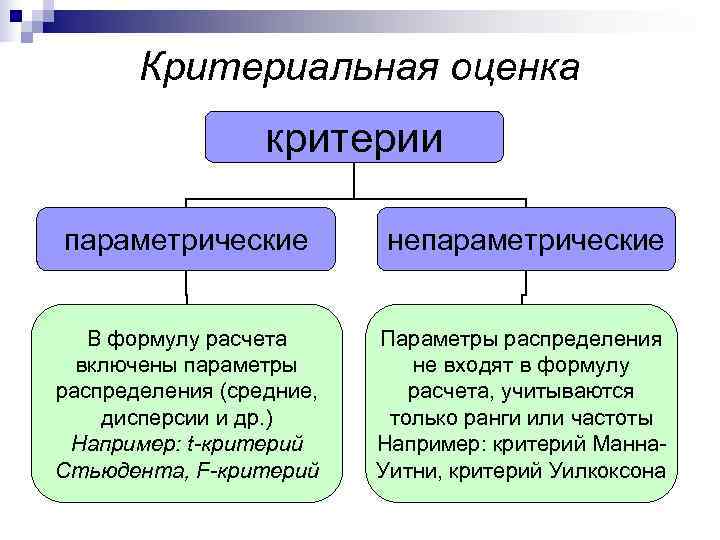
Критериальная оценка критерии параметрические непараметрические В формулу расчета Параметры распределения включены параметры не входят в формулу распределения (средние, расчета, учитываются дисперсии и др. ) только ранги или частоты Например: t-критерий Например: критерий Манна- Стьюдента, F-критерий Уитни, критерий Уилкоксона
вспомнить 1 семестр.ppt
- Количество слайдов: 24

