cd203c7c4936d5817e8b555a40b827f8.ppt
- Количество слайдов: 52

ESCHOOL/Advanced Study Institute - PHYSBIO 3 Benasque 2003 Symmetry breaking instabilities in granular gases. Lectures I and II. Baruch Meerson Hebrew University of Jerusalem, Israel Plan 1. 2. 3. 4. 5. 6. Examples of symmetry breaking instabilities + motivation. Granular hydrodynamics (a brief overview). Thermal granular convection. Phase separation. Giant fluctuations at onset of phase separation: is hydrodynamics sufficient? Summary

A few pictures of the Hebrew University of Jerusalem

A few pictures of Jerusalem

Example 1. Granular Maxwell’s Demon: phase separation by symmetry breaking Schlichting and Nordmeier (1996), Eggers (1999), Lohse et al. (2001), Brey et al. (2002), … original experiment theory more experiment + theory

Granular Maxwell’s Demon (continued): coarsening Lohse et al. (2002) Coarsening will be considered in Lecture 3.
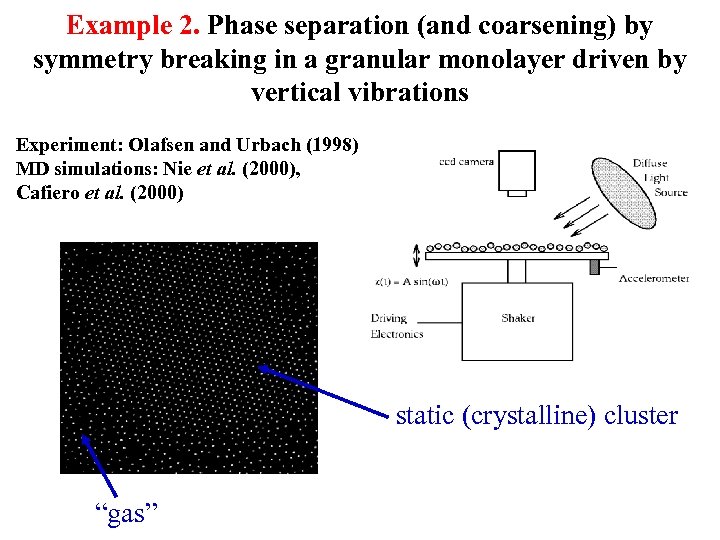
Example 2. Phase separation (and coarsening) by symmetry breaking in a granular monolayer driven by vertical vibrations Experiment: Olafsen and Urbach (1998) MD simulations: Nie et al. (2000), Cafiero et al. (2000) static (crystalline) cluster “gas”

Before going further: Gas of Inelastic Hard Spheres s: particle diameter m: particle mass inelastic binary collisions (simplest model) coefficient of normal restitution: coefficient of normal restitution

In most cases, this model cannot describe granular solids: It does describe many aspects of granular liquids: and, of course, granular gas.
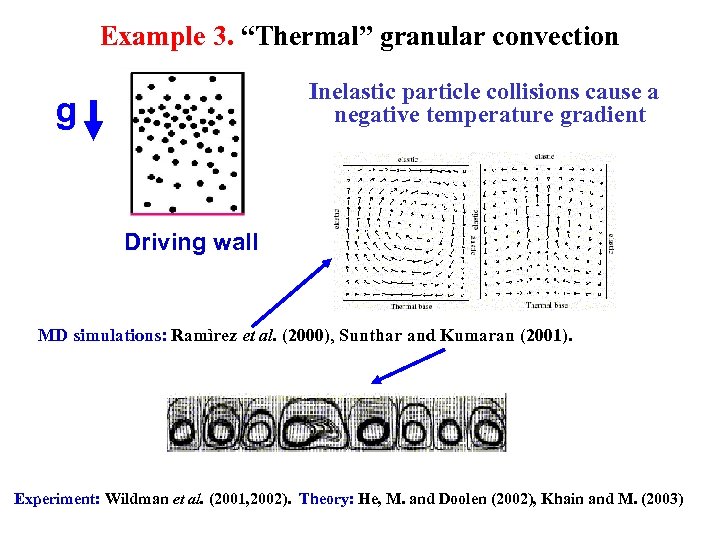
Example 3. “Thermal” granular convection Inelastic particle collisions cause a negative temperature gradient g Driving wall MD simulations: Ramìrez et al. (2000), Sunthar and Kumaran (2001). Experiment: Wildman et al. (2001, 2002). Theory: He, M. and Doolen (2002), Khain and M. (2003)

Example 4. Clustering in a freely cooling granular gas Goldhirsch and Zanetti (1993) Strongly inelastic collisions, narrow cluster bands (few particle diameters) density map Luding (2002) Nearly elastic collisions, 1 -r<<1 much wider cluster bands: Granular Hydrodynamics has better chances to be valid

Motivation: why should we care about symmetry breaking instabilities (SBIs)? • SBIs provide sensitive tests to models of granular flows • They improve our understanding of pattern formation far from equilibrium • They are cool

II. Navier-Stokes granular hydrodynamics (GH): an overview GH operates with three coarse-grained fields: r (r, t): granular density v(r, t): granular velocity T(r, t): granular temperature a compressible fluid! Formal definitions: n(r, t): local number density Averaging over cells that are small compared to the system size, but still include many particles

Equations of Navier-Stokes GH mass conservation momentum conservation energy equation d=2 or 3: P: stress tensor dimension of space Q: heat flux G: rate of energy loss by collisions per unit volume f: external force More fundamental kinetic theory validates these equations and supplies constitutive relations: Jenkins and Richman, Tan and Goldhirsch, Brey et al.

“Standard” constitutive relations of GH Jenkins and Richman (1985, 1988) rate of deformation tensor deviatoric part of D G, F, J and M: functions of nps 2 (d=2), or nps 3(d=3) a 1, a 2, a 3, a 4 and a 5, : numbers Conveniently presented by Babić (1993) Valid for nearly elastic collisions, 1 -r<<1, and at small or moderate densities

The energy sink term G: a simple estimate Energy lost in each collision: A particle with speed v. T~ (T/m)1/2 loses, on the average, energy ~ m (1 -r 2) v. T 2. Collision rate ~ v. T/l, where l is the mean free path. n particles in unit volume. d=2, dilute limit

When is the Navier-Stokes GH valid? Not a simple question. Important necessary conditions are: 1. Mean free path and particle diameter are small compared to any length scale described hydrodynamically. 2. Mean time between two consecutive collisions are small compared to any time scale described hydrodynamically. 3. Only single, liquid-like phase. 4. Velocity distribution function f(v, r, t) is “close to Maxwellian” at all r and t of interest. 5. Inelastic collapse doesn’t happen (or removed by a regularization). 1, 2, 4 and 5 are usually satisfied for nearly elastic collisions, 1 -r<<1 (quite a restrictive condition! OK for glass balls, steel balls. ) 3 is expected to break down at high densities. In general, this requires introduction of an order parameter into theory, cf. Aranson and Tsimring (2002), even for the hard sphere model. Sometimes, condition 3 can be relaxed: Grossman et al. (1997), M. , Pöschel and Bromberg (2003), Gollub et al… Not always clear why.
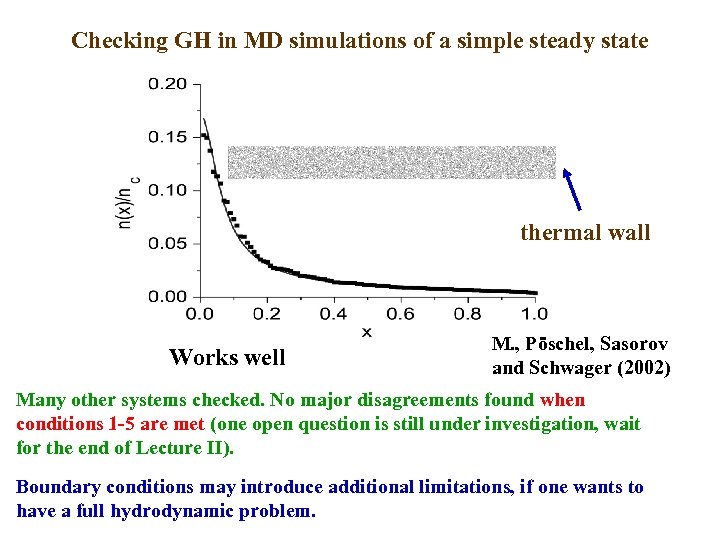
Checking GH in MD simulations of a simple steady state thermal wall Works well M. , Pöschel, Sasorov and Schwager (2002) Many other systems checked. No major disagreements found when conditions 1 -5 are met (one open question is still under investigation, wait for the end of Lecture II). Boundary conditions may introduce additional limitations, if one wants to have a full hydrodynamic problem.

Relaxing condition 3: close-packed “floating”cluster experiment Lohse et al. (2003) MD simulations M. , Pöschel and Bromberg (2003)
![A simple version of Granular Hydrostatics [Grossman, Zhou and Ben-Naim (1997)] works well at A simple version of Granular Hydrostatics [Grossman, Zhou and Ben-Naim (1997)] works well at](https://present5.com/presentation/cd203c7c4936d5817e8b555a40b827f8/image-19.jpg)
A simple version of Granular Hydrostatics [Grossman, Zhou and Ben-Naim (1997)] works well at all densities, up to hexagonal close packing g T=const Phase coexistence doesn’t seem to play a big role here M. , Pöschel and Bromberg (2003)
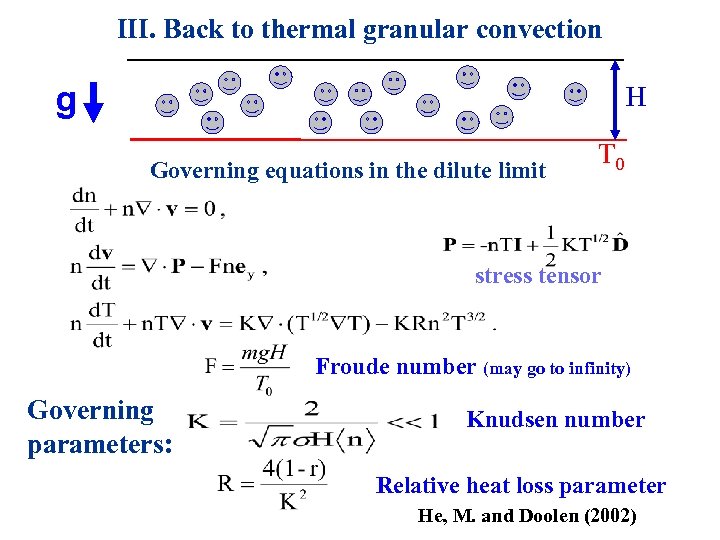
III. Back to thermal granular convection g H Governing equations in the dilute limit T 0 stress tensor Froude number (may go to infinity) Governing parameters: Knudsen number Relative heat loss parameter He, M. and Doolen (2002)
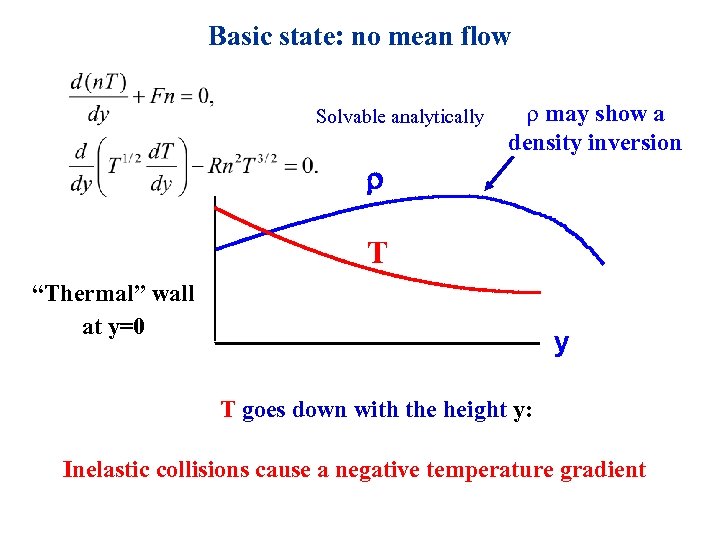
Basic state: no mean flow Solvable analytically r may show a density inversion r T “Thermal” wall at y=0 y T goes down with the height y: Inelastic collisions cause a negative temperature gradient
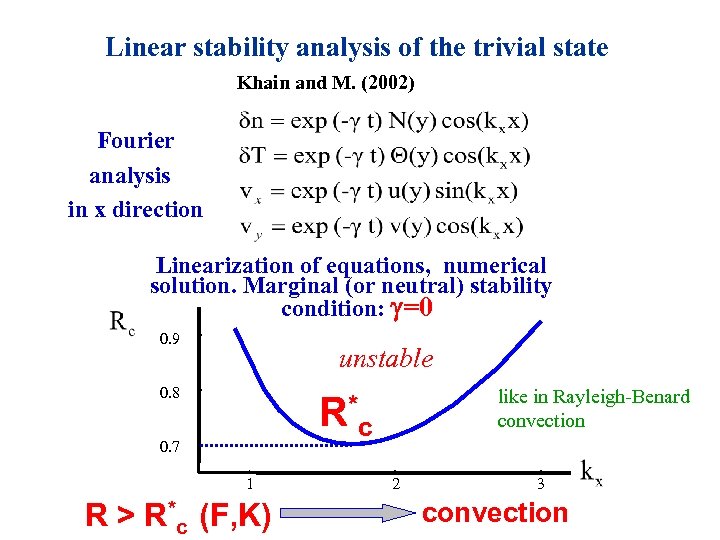
Linear stability analysis of the trivial state Khain and M. (2002) Fourier analysis in x direction Linearization of equations, numerical solution. Marginal (or neutral) stability condition: g=0 0. 9 unstable 0. 8 R* 0. 7 1 R > R*c (F, K) like in Rayleigh-Benard convection c 2 3 convection
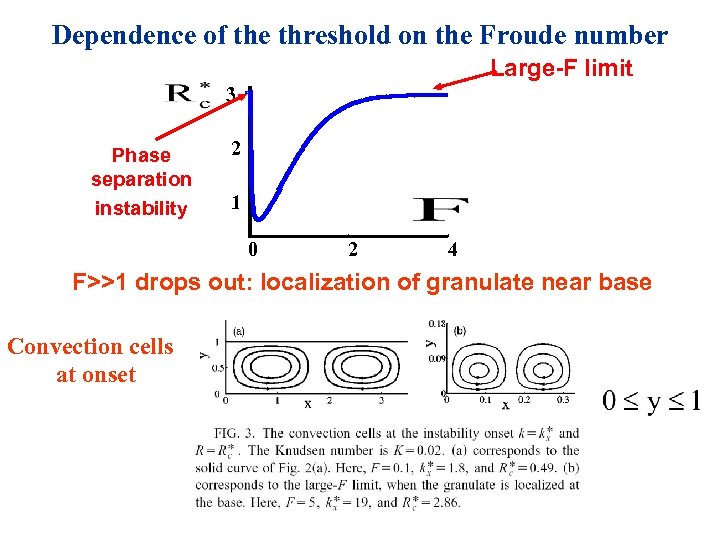
Dependence of the threshold on the Froude number Large-F limit 3 Phase separation instability 2 1 0 2 4 F>>1 drops out: localization of granulate near base Convection cells at onset

Schwarzschild’s criterion for classical convection in compressible fluid S: entropy of fluid no convection
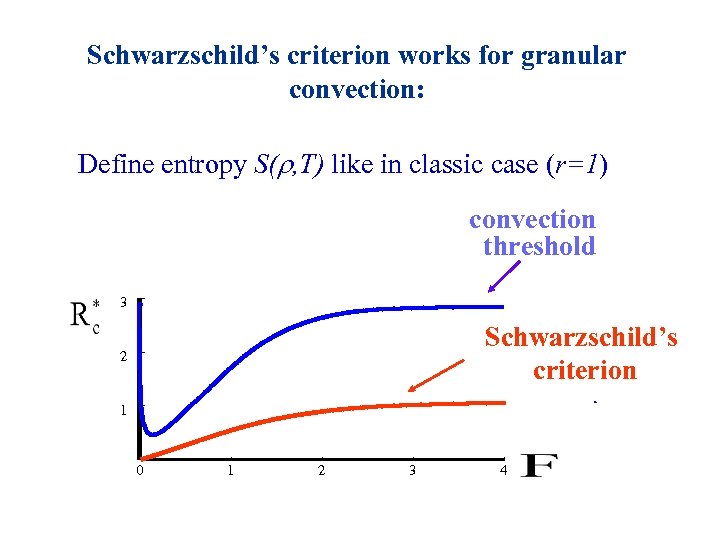
Schwarzschild’s criterion works for granular convection: Define entropy S(r, T) like in classic case (r=1) convection threshold 3 Schwarzschild’s criterion 2 1 0 1 2 3 4
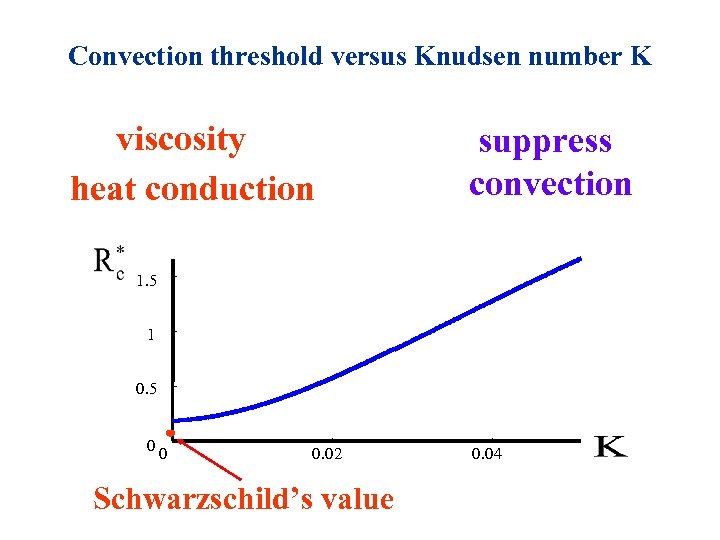
Convection threshold versus Knudsen number K viscosity heat conduction suppress convection 1. 5 1 0. 5 00 0. 02 Schwarzschild’s value 0. 04
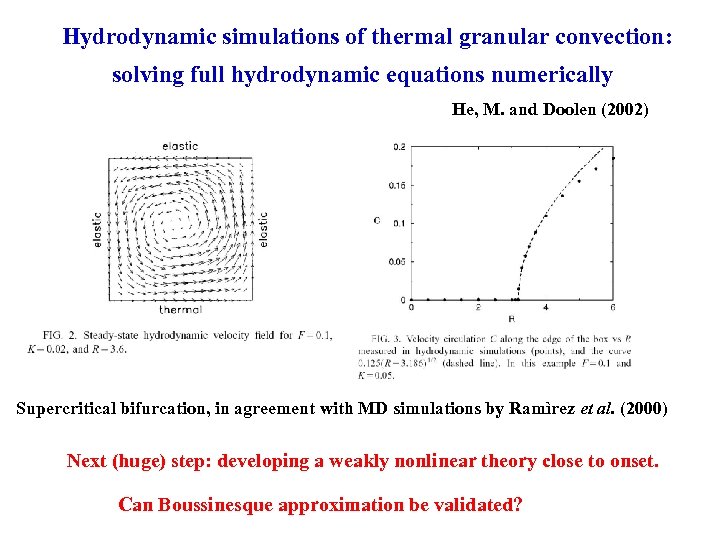
Hydrodynamic simulations of thermal granular convection: solving full hydrodynamic equations numerically He, M. and Doolen (2002) Supercritical bifurcation, in agreement with MD simulations by Ramìrez et al. (2000) Next (huge) step: developing a weakly nonlinear theory close to onset. Can Boussinesque approximation be validated?
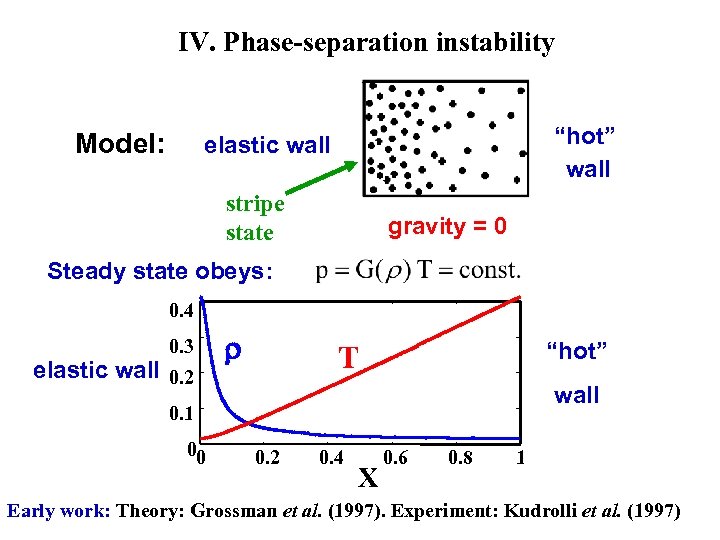
IV. Phase-separation instability Model: “hot” wall elastic wall stripe state gravity = 0 Steady state obeys: 0. 4 0. 3 elastic wall 0. 2 r “hot” T wall 0. 1 00 0. 2 0. 4 X 0. 6 0. 8 1 Early work: Theory: Grossman et al. (1997). Experiment: Kudrolli et al. (1997)

GH predicts instability of the stripe state, 2 D steady states appear. Livne, M. and Sasorov (2000, 2002), Khain and M. (2002) Steady-state describable by hydrostatic equations: heat conduction heat loss Stripe state: 1 D solution of these eqns. nonlinear problem multiple hydrostatic solutions possible, stripe can be unstable or metastable

Governing parameters of the hydrostatic equations hydrodynamic heat loss parameter area fraction aspect ratio Livne, M. and Sasorov (2000, 2002); Khain and M. (2002)
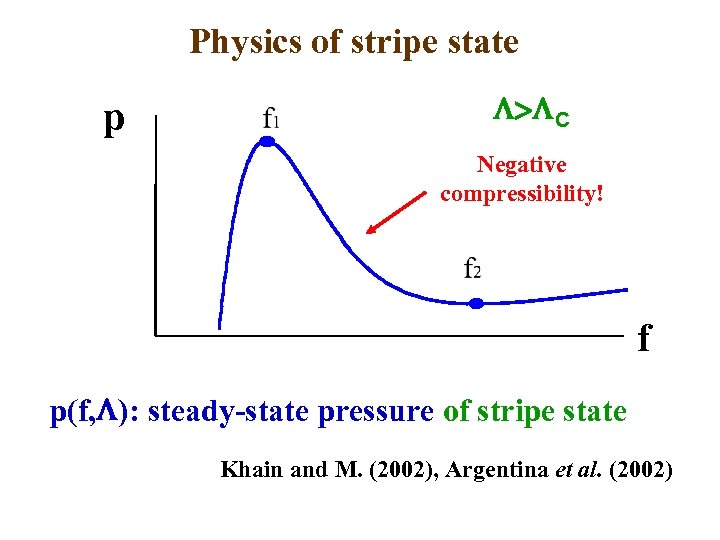
Physics of stripe state p > C Negative compressibility! f p(f, ): steady-state pressure of stripe state Khain and M. (2002), Argentina et al. (2002)
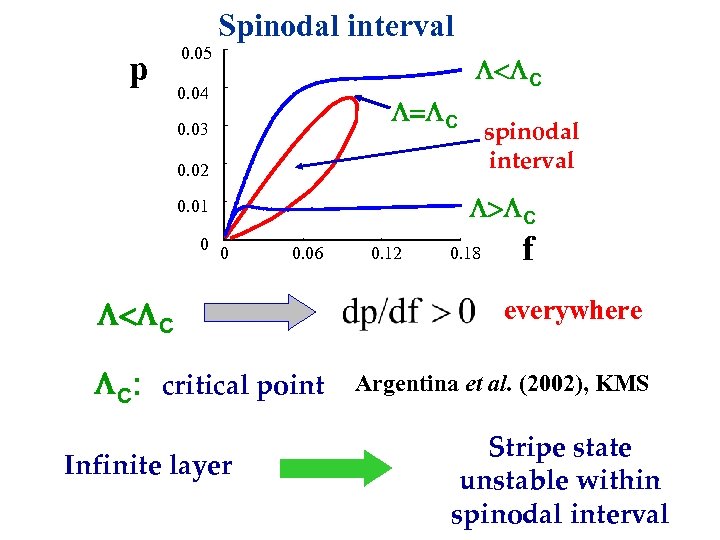
p 0. 05 Spinodal interval < C 0. 04 = C 0. 03 spinodal interval 0. 02 > C 0. 01 0 0 0. 06 < C C: critical point Infinite layer 0. 12 0. 18 f everywhere Argentina et al. (2002), KMS Stripe state unstable within spinodal interval
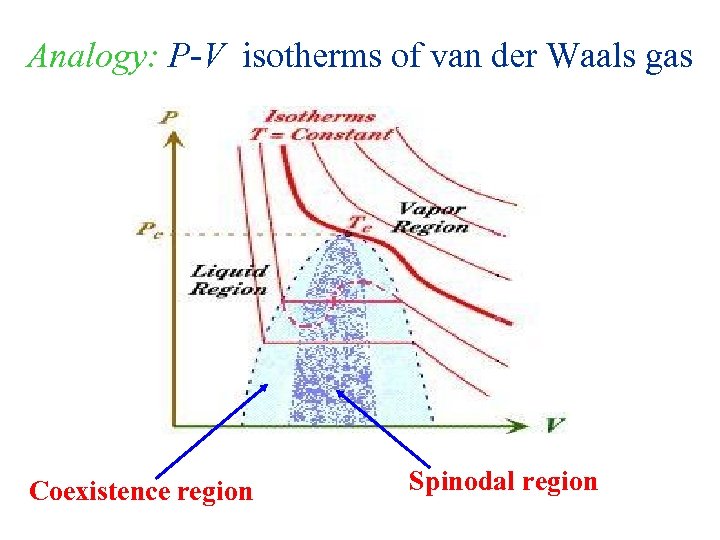
Analogy: P-V isotherms of van der Waals gas Coexistence region Spinodal region
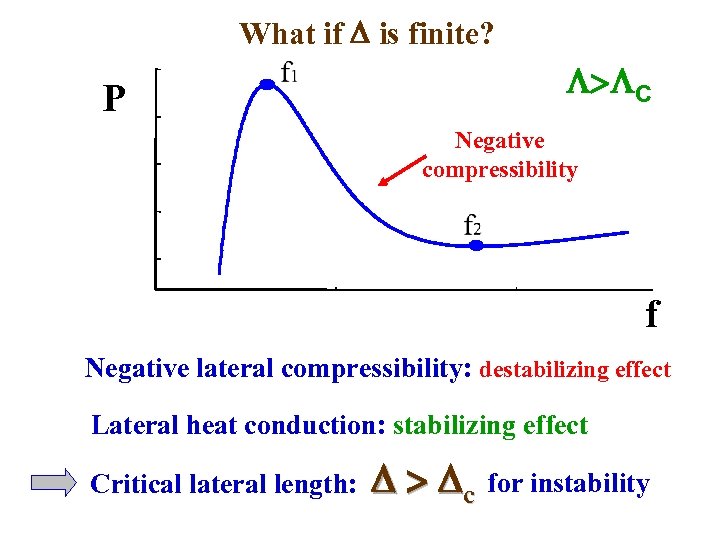
What if is finite? P > C Negative compressibility f Negative lateral compressibility: destabilizing effect Lateral heat conduction: stabilizing effect Critical lateral length: > c for instability

How to find c , the critical lateral length for instability? Marginal stability analysis Close to continuous bifurcation threshold scaled inverse density k is small linearization of hydrostatic eqns. Schrödinger equation for k(x) k: discrete energy level KM 2002
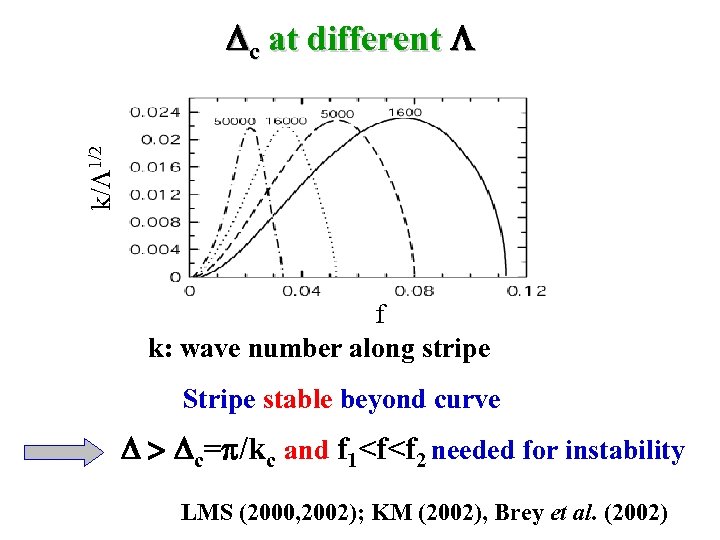
k/ 1/2 c at different f k: wave number along stripe Stripe stable beyond curve > c=p/kc and f 1<f<f 2 needed for instability LMS (2000, 2002); KM (2002), Brey et al. (2002)
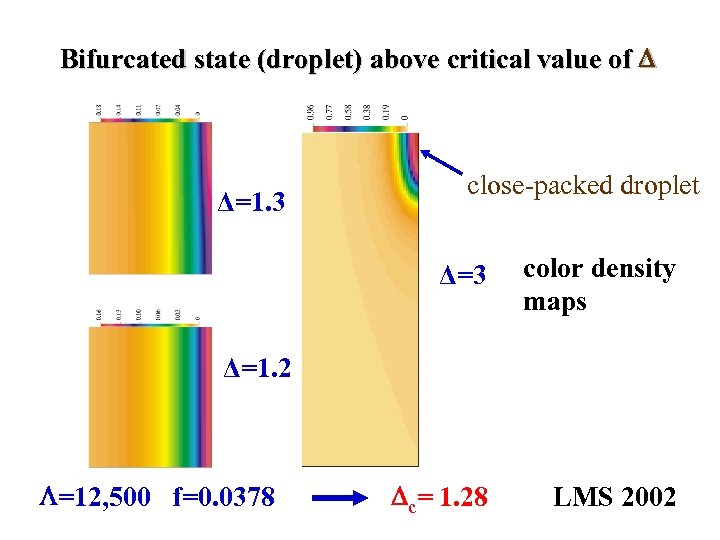
Bifurcated state (droplet) above critical value of Δ=1. 3 close-packed droplet Δ=3 color density maps c= 1. 28 LMS 2002 Δ=1. 2 =12, 500 f=0. 0378
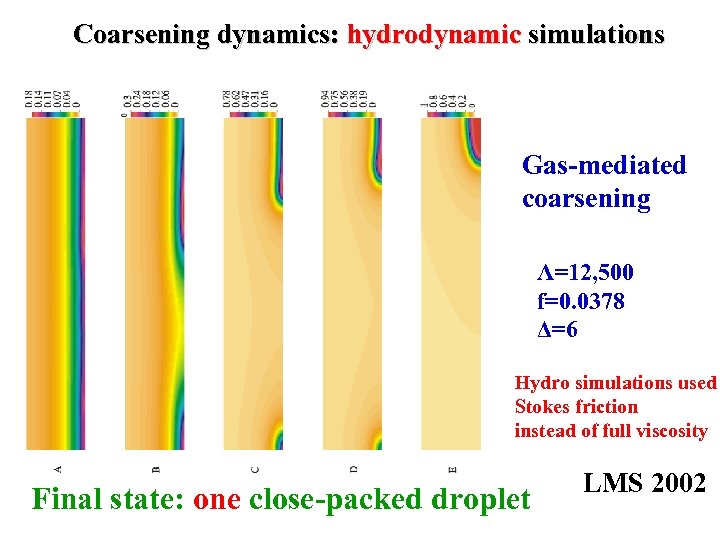
Coarsening dynamics: hydrodynamic simulations Gas-mediated coarsening Λ=12, 500 f=0. 0378 Δ=6 Hydro simulations used Stokes friction instead of full viscosity Final state: one close-packed droplet LMS 2002
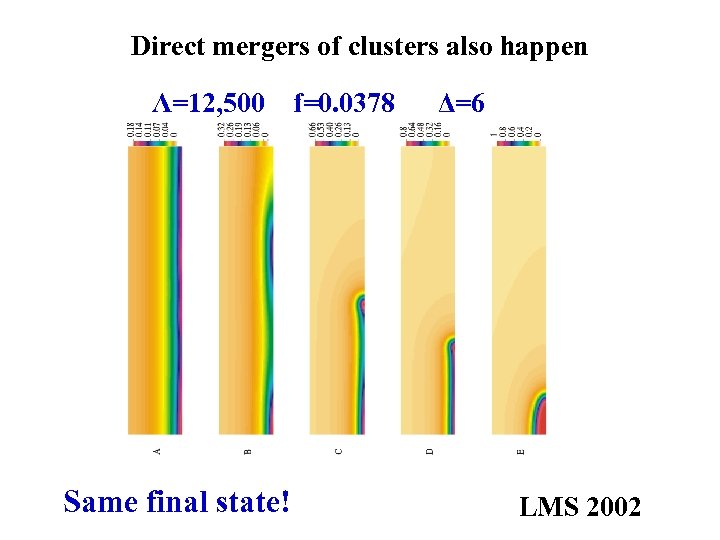
Direct mergers of clusters also happen Λ=12, 500 Same final state! f=0. 0378 Δ=6 LMS 2002
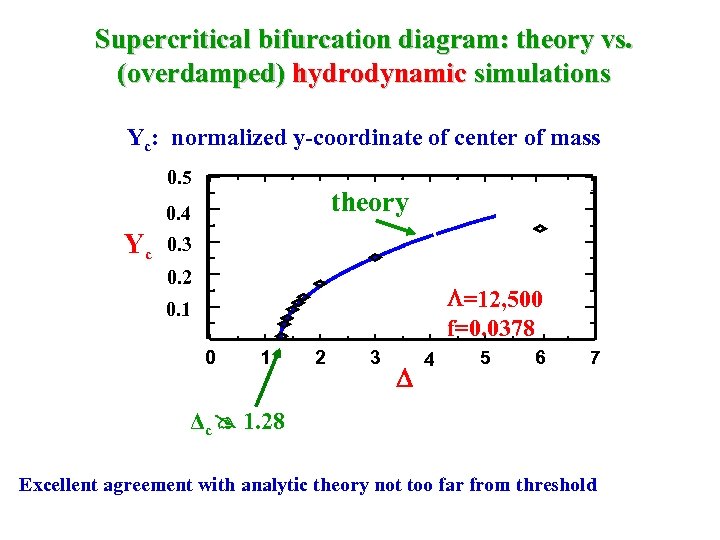
Supercritical bifurcation diagram: theory vs. (overdamped) hydrodynamic simulations Yc: normalized y-coordinate of center of mass 0. 5 theory 0. 4 Yc 0. 3 0. 2 =12, 500 f=0. 0378 0. 1 0 1 2 3 4 5 6 7 Δc 1. 28 Excellent agreement with analytic theory not too far from threshold
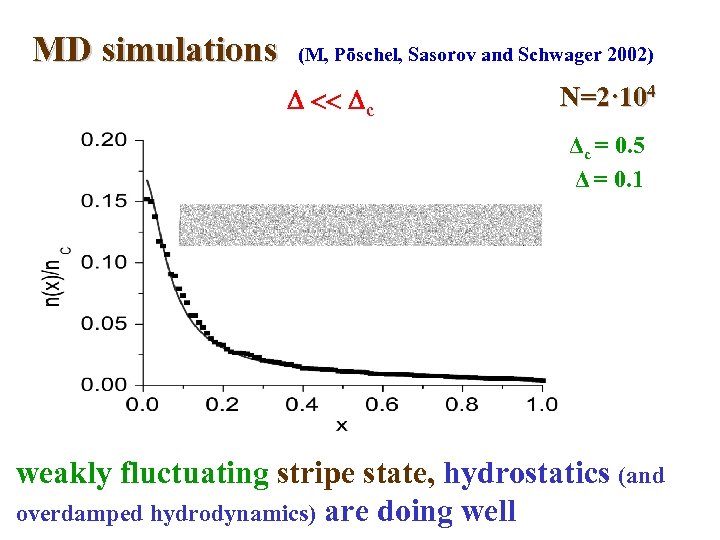
MD simulations (M, Pöschel, Sasorov and Schwager 2002) << c N=2· 104 Δc = 0. 5 Δ = 0. 1 weakly fluctuating stripe state, hydrostatics (and overdamped hydrodynamics) are doing well
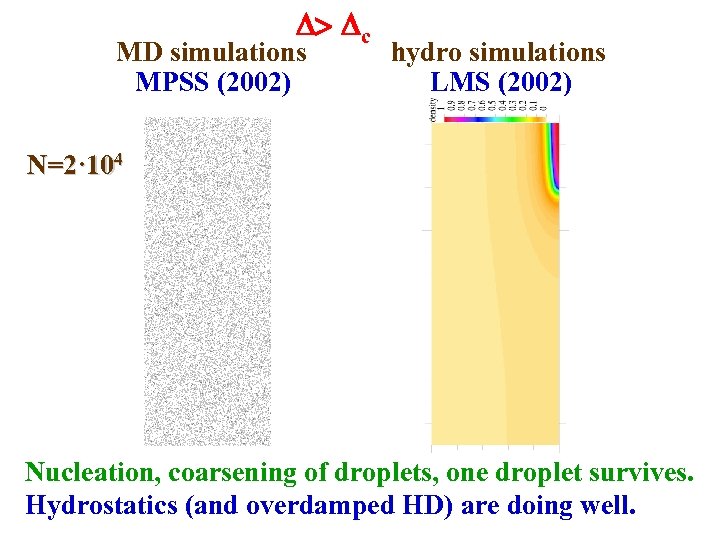
> c MD simulations MPSS (2002) hydro simulations LMS (2002) N=2· 104 Nucleation, coarsening of droplets, one droplet survives. Hydrostatics (and overdamped HD) are doing well.

Very large aspect ratio: >> c MD simulations Argentina et al. (2002) fluctuations weak, hydrostatics OK Outside of spinodal interval, inside coexistence interval

What happens around ~ c? MD simulations N=2· 104 Transitions between the two states with broken symmetry?
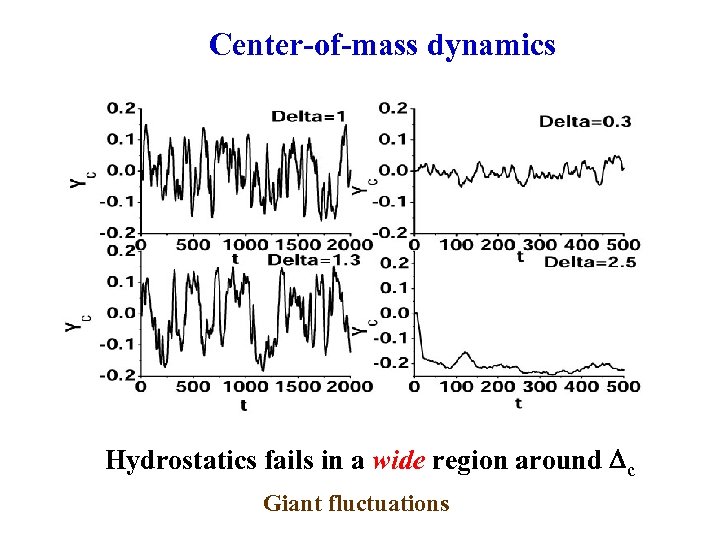
Center-of-mass dynamics Hydrostatics fails in a wide region around c Giant fluctuations

Probability distribution of Yc at different Symmetry-breaking transition occurs somewhere at 0. 3 < < 1, hydrostatics predicts c = 0. 5.
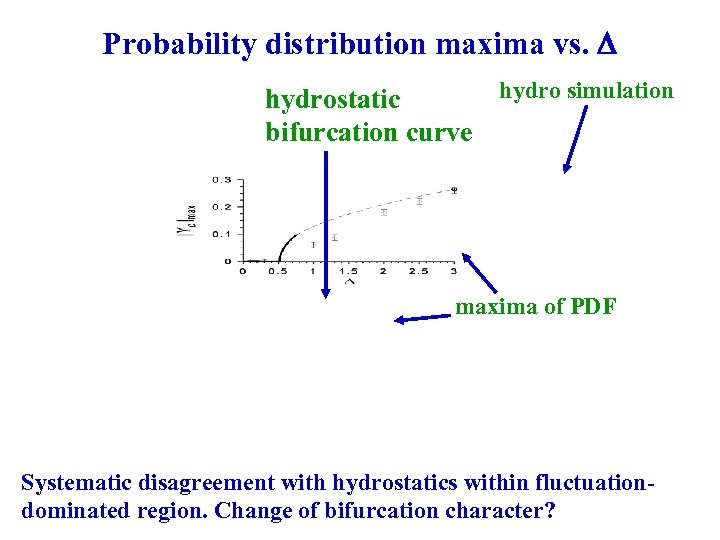
Probability distribution maxima vs. hydro simulation hydrostatic bifurcation curve maxima of PDF Systematic disagreement with hydrostatics within fluctuationdominated region. Change of bifurcation character?
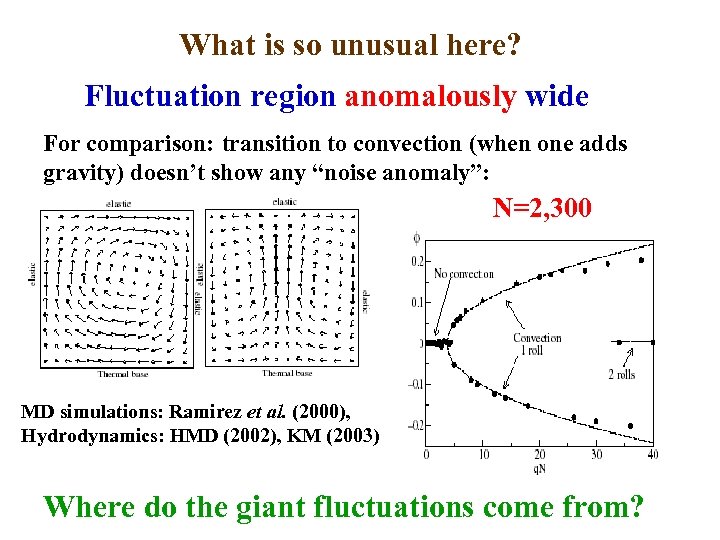
What is so unusual here? Fluctuation region anomalously wide For comparison: transition to convection (when one adds gravity) doesn’t show any “noise anomaly”: N=2, 300 MD simulations: Ramirez et al. (2000), Hydrodynamics: HMD (2002), KM (2003) Where do the giant fluctuations come from?
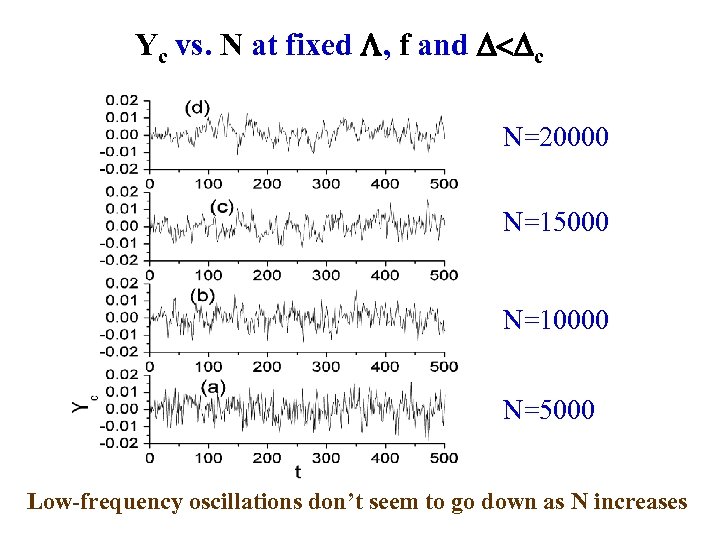
Yc vs. N at fixed , f and < c N=20000 N=15000 N=10000 N=5000 Low-frequency oscillations don’t seem to go down as N increases

Scenario I. Giant fluctuations are driven hydrodynamically: by a (yet unknown) instability (Ia), or by a long-lived transient (Ib) To check this scenario, one needs full hydrodynamic simulations (Livne, M. and Sasorov; work in progress).

Scenario II. Amplification of discrete-particle noise. Here “Fluctuating Granular Hydrodynamics” is needed Now P, q and G include deltacorrelated gaussian random noise terms, in the spirit of Landau and Lifshitz (1959). Nasty surprise: noise part of G is not known! Once it is computed we can start working, but: the problem is difficult because of mode coupling: two acoustic modes, entropy mode and shear mode. Further simplifications needed: very small or large aspect ratio, work close to the critical point, … Hopefully, Scenario I is correct!

Conclusions 1. 2. 3. 4. Symmetry-breaking instabilities (SBIs) are sensitive probes of models of granular flow SBIs are ubiquitous in granular gases Two particular and novel SBIs discussed in Lectures 1 and 2: thermal granular convection and phase separation A whole lot of work remains to be done: convection: Boussinesque (? ), weakly-nonlinear theory close to onset, phase separation: giant fluctuations, role of oscillatory instability: yesterday’s talk by Evgeniy Khain Finally, a take-home message about Granular Hydrodynamics: 5. When it can be used, it must be used
cd203c7c4936d5817e8b555a40b827f8.ppt