Error Correction and LDPC decoding CMPE 691 491 DSP

Error Correction and LDPC decoding CMPE 691/491: DSP Hardware Implementation Tinoosh Mohsenin 1

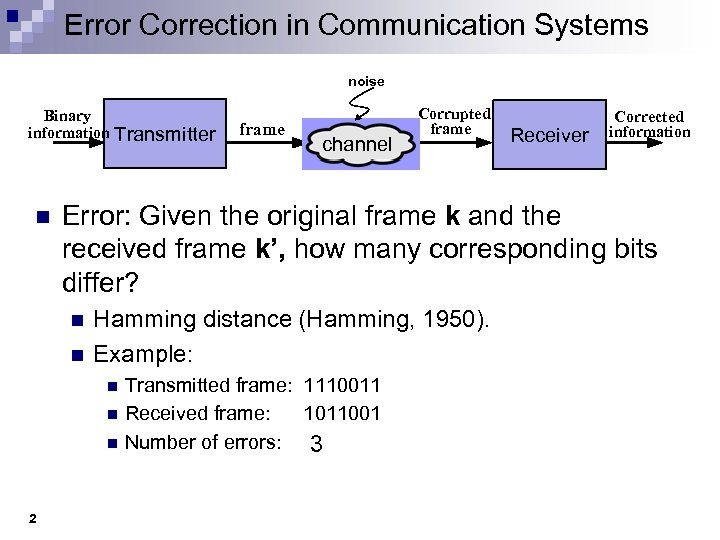Error Correction in Communication Systems noise Binary information Transmitter n channel Receiver Corrected information Error: Given the original frame k and the received frame k’, how many corresponding bits differ? n n Hamming distance (Hamming, 1950). Example: n n n 2 frame Corrupted frame Transmitted frame: 1110011 Received frame: 1011001 Number of errors: 3

Error Detection and Correction n Add extra information to the original data being transmitted. n n Error detection: enough info to detect error. n n Frame = k data bits + m bits for error control: n = k + m. Need retransmissions. Error correction: enough info to detect and correct error. n Forward error correction (FEC). 3

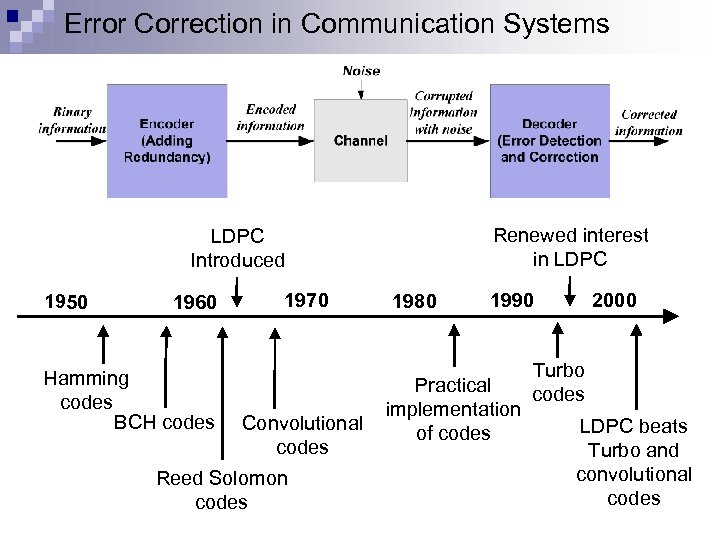Error Correction in Communication Systems Renewed interest in LDPC Introduced 1950 1960 1970 1980 1990 2000 Turbo Practical codes implementation Convolutional LDPC beats of codes Turbo and convolutional Reed Solomon codes Hamming codes BCH codes

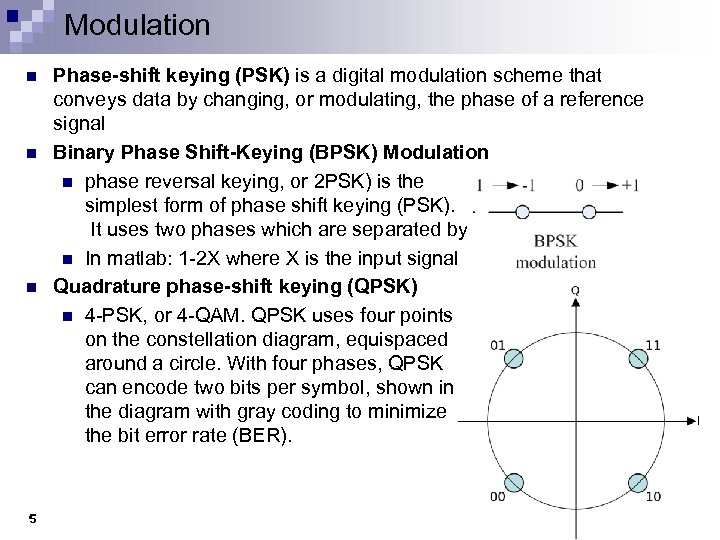Modulation n 5 Phase-shift keying (PSK) is a digital modulation scheme that conveys data by changing, or modulating, the phase of a reference signal Binary Phase Shift-Keying (BPSK) Modulation n phase reversal keying, or 2 PSK) is the simplest form of phase shift keying (PSK). It uses two phases which are separated by 180° n In matlab: 1 -2 X where X is the input signal Quadrature phase-shift keying (QPSK) n 4 -PSK, or 4 -QAM. QPSK uses four points on the constellation diagram, equispaced around a circle. With four phases, QPSK can encode two bits per symbol, shown in the diagram with gray coding to minimize the bit error rate (BER).

Key terms n n n Encoder : adds redundant bits to the sender's bit stream to create a codeword. Decoder: uses the redundant bits to detect and/or correct as many bit errors as the particular error-control code will allow. Communication Channel: the part of the communication system that introduces errors. n Ex: radio, twisted wire pair, coaxial cable, fiber optic cable, magnetic tape, optical discs, or any other noisy medium n Additive white Gaussian noise (AWGN) n Larger noise makes the distribution wider 6

Important metrics n Bit error rate (BER): The probability of bit error. n n n We want to keep this number small Ex: BER=10 -4 means if we have transmitted 10, 000 bits, there is 1 bit error. BER is a useful indicator of system performance independent of error channel BER=Number of error bits/ total number of transmitted bits Signal to noise ratio (SNR): quantifies how much a signal has been corrupted by noise. n defined as the ratio of signal power to the noise power corrupting the signal. A ratio higher than 1: 1 indicates more signal than noise often expressed using the logarithmic decibel scale: n Important number: 3 d. B means signal power is two times noise power n 7

Error Correction in Communication Systems Information k -bit n n n Goal: Attain lower BER at smaller SNR Error correction is a key component 100 in communication and storage applications. 10 -1 Coding example: Convolutional, Turbo, and Reed-Solomon codes 10 -2 What can 3 d. B of coding gain buy? n n 8 channel Receivedword n-bit A satellite can send data with half the required transmit power A cellphone can operate reliably with half the required receive power Bit Error Probability n Encoder (add parity) Codeword n-bit noise 10 -3 10 -4 Decoder (check parity, detect error) Corrected Information k-bit Uncoded system Convolutional code 3 d. B 0 1 2 3 4 5 6 7 8 Signal to Noise Ratio (d. B) Figure courtesy of B. Nikolic, 2003 (modified)

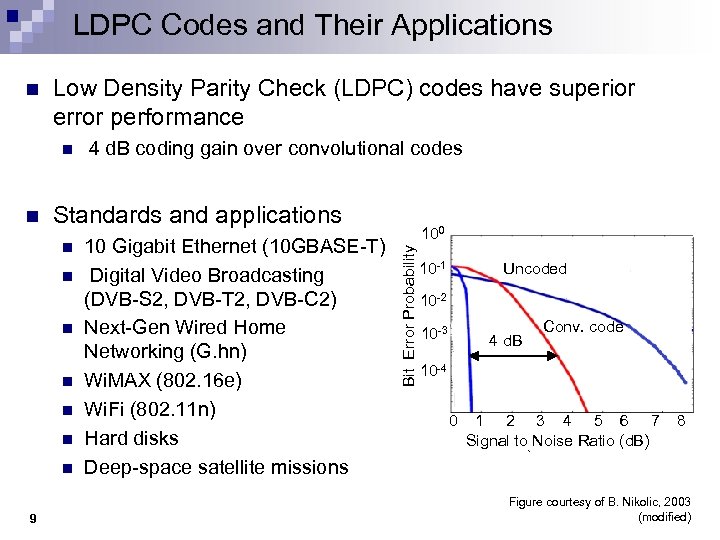LDPC Codes and Their Applications Low Density Parity Check (LDPC) codes have superior error performance n n Standards and applications n n n n 9 4 d. B coding gain over convolutional codes 100 10 Gigabit Ethernet (10 GBASE-T) Uncoded 10 -1 Digital Video Broadcasting (DVB-S 2, DVB-T 2, DVB-C 2) 10 -2 Conv. code Next-Gen Wired Home 10 -3 4 d. B Networking (G. hn) 10 -4 Wi. MAX (802. 16 e) Wi. Fi (802. 11 n) 0 1 2 3 4 5 6 7 8 Hard disks Signal to Noise Ratio (d. B) Deep-space satellite missions Bit Error Probability n Figure courtesy of B. Nikolic, 2003 (modified)

Encoding Picture Example V= H. Vi. T=0 Parity Image Binary multiplication called syndrome check

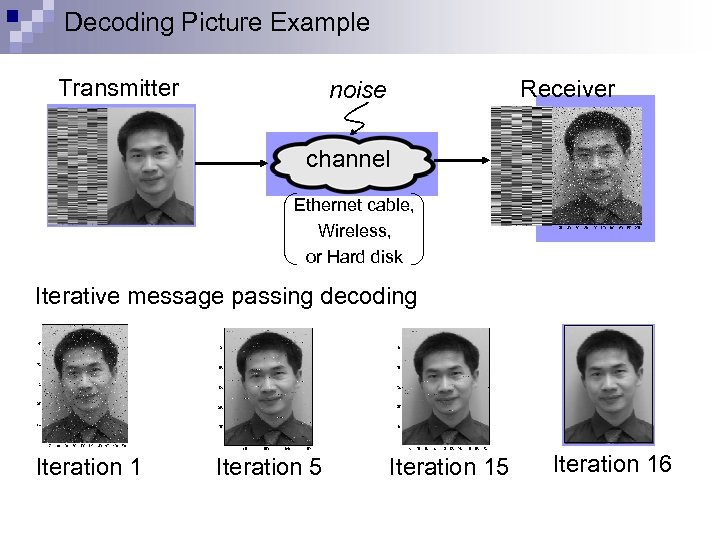Decoding Picture Example Transmitter Receiver noise channel Ethernet cable, Wireless, or Hard disk Iterative message passing decoding Iteration 1 Iteration 5 Iteration 16

LDPC Codes—Parity Check Matrix n Defined by a large binary matrix, called a parity check matrix or H matrix n n n Example: 6 x 12 H matrix for a 12 -bit LDPC code n n 12 Each row is defined by a parity equation The number of columns is the code length No. of columns=12 (i. e. Receivedword (V) = 12 bit) No. of rows= 6 No. of ones per row=3 (row weight) No. of ones per col= 2 (column weight)

LDPC Codes—Tanner Graph n Interconnect representation of H matrix n n Two sets of nodes: Check nodes and Variable nodes Each row of the matrix is represented by a Check node Each column of matrix is represented by a Variable node A message passing method is used between nodes to correct errors (1) Initialization with Receivedword (2) Messages passing until correct Example: V 3 to C 1, V 4 to C 1, V 8 to C 1, V 10 to C 1 C 2 to V 1, C 5 to V 1 The same for other nodes: message passing along the connections Variable nodes V 1 13 V 2 C 1 V 3 V 4 C 2 V 5 C 3 V 6 C 4 V 7 C 5 V 8 Receivedword from channel C 6 V 9 Check nodes V 10 V 11 V 12

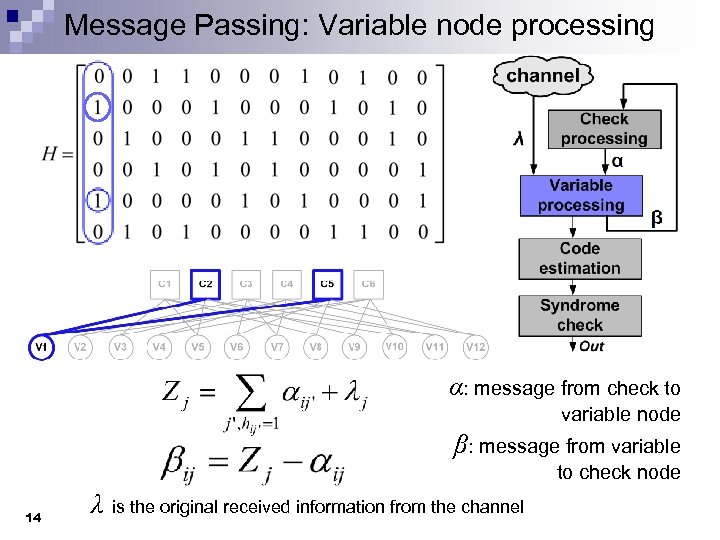Message Passing: Variable node processing α: message from check to variable node β: message from variable to check node 14 λ is the original received information from the channel

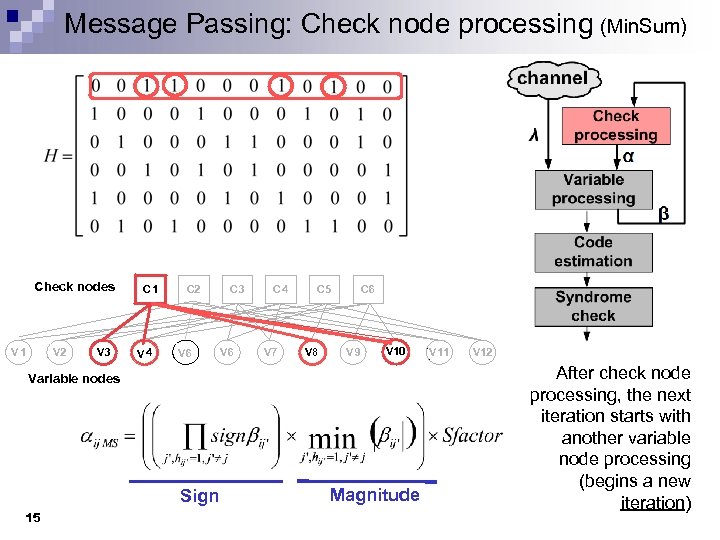Message Passing: Check node processing (Min. Sum) Check nodes V 1 V 2 V 3 C 1 V 4 C 2 V 6 C 3 V 6 C 4 V 7 C 5 V 8 C 6 V 9 V 10 Variable nodes Sign 15 Magnitude V 11 V 12 After check node processing, the next iteration starts with another variable node processing (begins a new iteration)

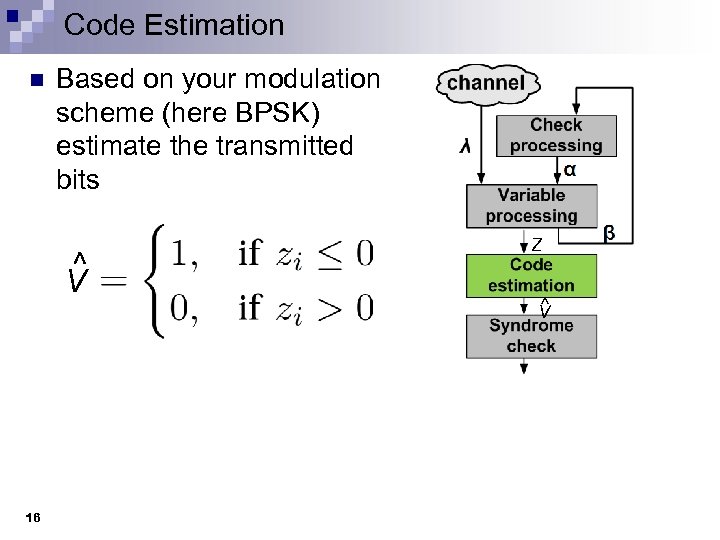Code Estimation n Based on your modulation scheme (here BPSK) estimate the transmitted bits ^ V 16 Z ^ V

Syndrome Check n Compute syndrome ^ H. Vi. T=0 (Binary multiplication) n Ex: n n 17 If syndrome =0, terminate decoding Else, continue another iteration

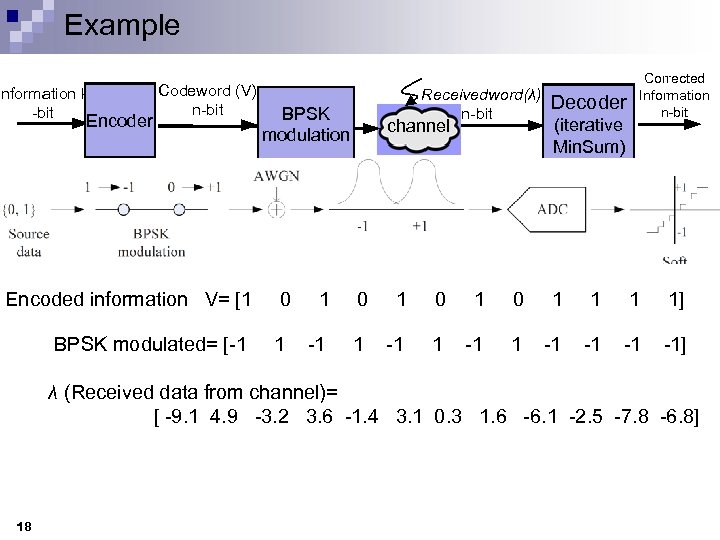Example Information k -bit Encoder Codeword (V) n-bit BPSK modulation Receivedword(λ) n-bit channel Decoder (iterative Min. Sum) Corrected Information n-bit Encoded information V= [1 0 1 0 1 1 1 1] BPSK modulated= [-1 1 -1 -1 -1] λ (Received data from channel)= [ -9. 1 4. 9 -3. 2 3. 6 -1. 4 3. 1 0. 3 1. 6 -6. 1 -2. 5 -7. 8 -6. 8] Estimated code= ^ V= 1 0 1 0 0 0 1 1 18

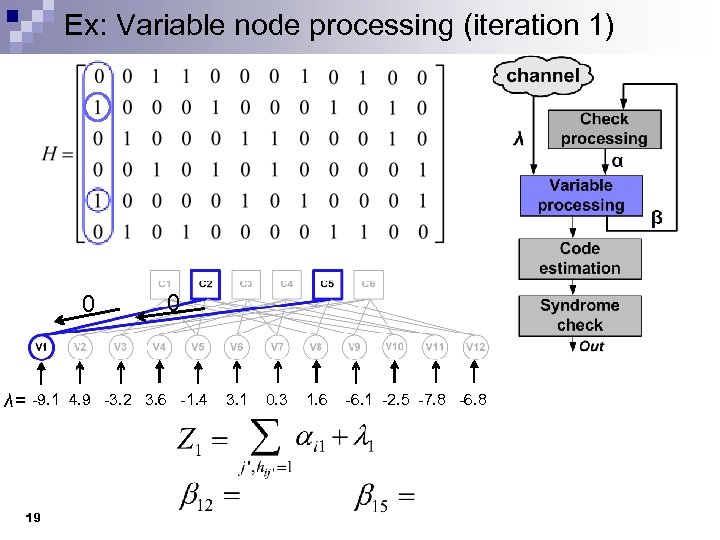Ex: Variable node processing (iteration 1) 0 0 λ= -9. 1 4. 9 -3. 2 3. 6 -1. 4 3. 1 0. 3 1. 6 -6. 1 -2. 5 -7. 8 -6. 8 19

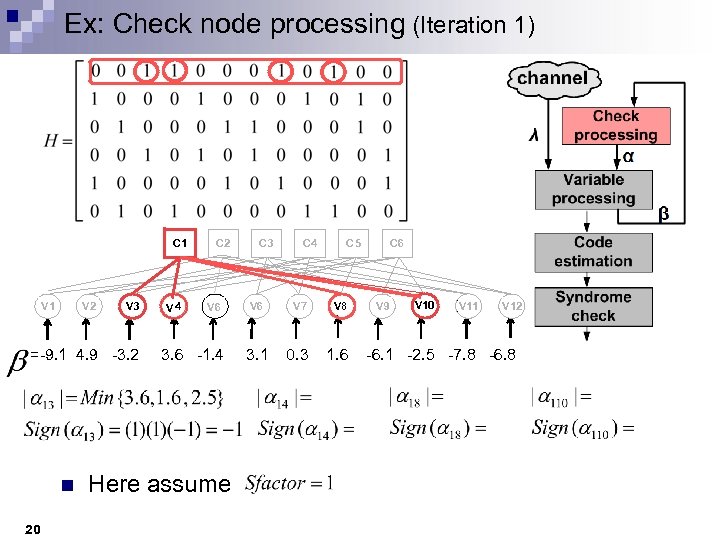Ex: Check node processing (Iteration 1) C 1 V 2 V 3 V 4 C 2 V 6 C 3 V 6 C 4 V 7 C 5 V 8 C 6 V 9 V 10 V 11 V 12 =-9. 1 4. 9 -3. 2 3. 6 -1. 4 3. 1 0. 3 1. 6 -6. 1 -2. 5 -7. 8 -6. 8 n 20 Here assume

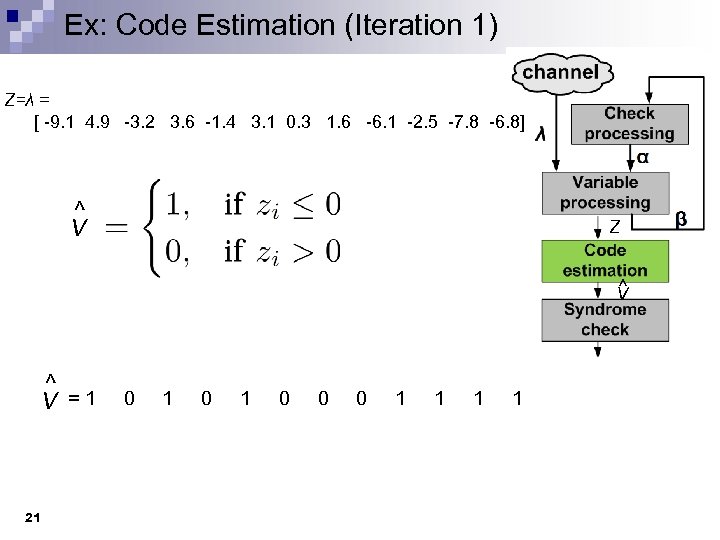Ex: Code Estimation (Iteration 1) Z=λ = [ -9. 1 4. 9 -3. 2 3. 6 -1. 4 3. 1 0. 3 1. 6 -6. 1 -2. 5 -7. 8 -6. 8] ^ V Z ^ V = 1 0 1 0 0 0 1 1 21

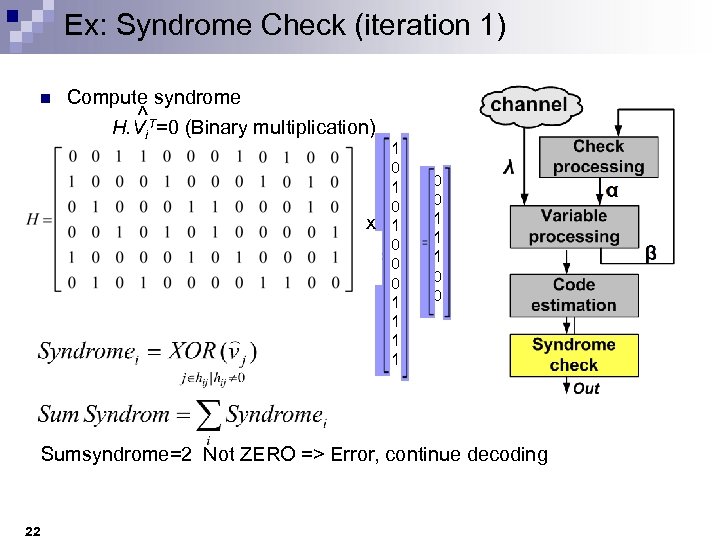Ex: Syndrome Check (iteration 1) n Compute syndrome ^ H. Vi. T=0 (Binary multiplication) x 1 0 1 0 0 0 1 1 1 0 0 Sumsyndrome=2 Not ZERO => Error, continue decoding 22

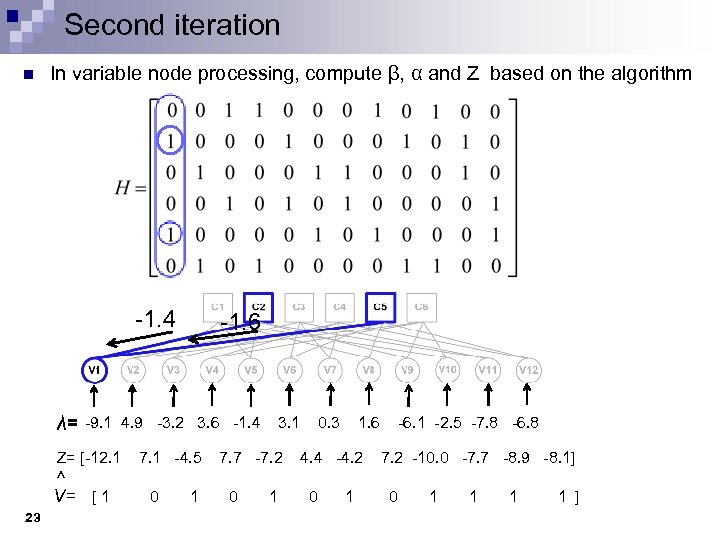Second iteration n In variable node processing, compute β, α and Z based on the algorithm -1. 4 -1. 6 λ= -9. 1 4. 9 -3. 2 3. 6 -1. 4 3. 1 0. 3 1. 6 -6. 1 -2. 5 -7. 8 -6. 8 Z= [-12. 1 7. 1 -4. 5 7. 7 -7. 2 4. 4 -4. 2 7. 2 -10. 0 -7. 7 -8. 9 -8. 1] ^ [ 1 0 1 0 1 1 1 ] V= 23

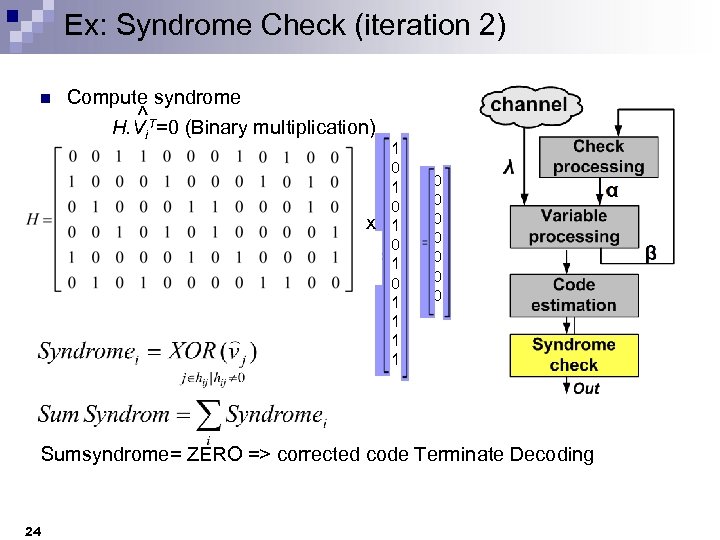Ex: Syndrome Check (iteration 2) n Compute syndrome ^ H. Vi. T=0 (Binary multiplication) x 1 0 1 0 1 1 0 0 0 0 Sumsyndrome= ZERO => corrected code Terminate Decoding 24

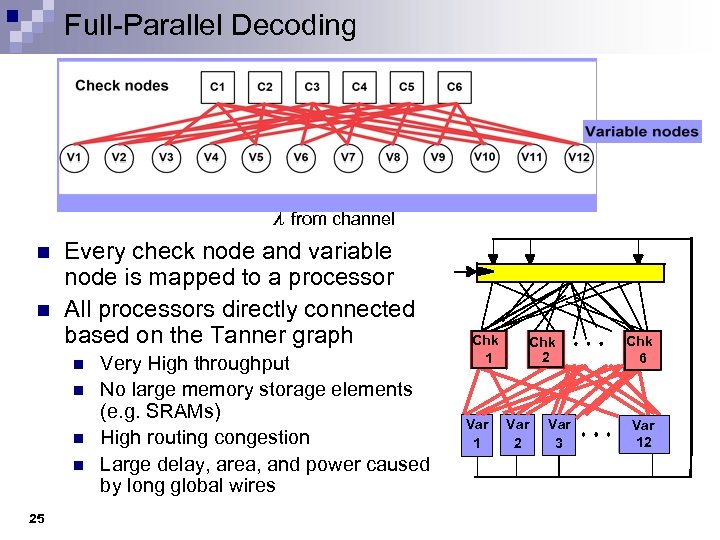Full-Parallel Decoding n n λ from channel Every check node and variable node is mapped to a processor All processors directly connected based on the Tanner graph n n 25 Very High throughput No large memory storage elements (e. g. SRAMs) High routing congestion Large delay, area, and power caused by long global wires Chk 1 init: all α = 0 Var 1 Chk 2 Var 3 Chk 5 6 Var 12

Full-Parallel LDPC Decoder Examples n n Ex 1: 1024 -bit decoder, [JSSC 2002] n 52. 5 mm 2, 50% logic utilization, 160 nm CMOS Ex 2: 2048 bit decoder, [ISCAS 2009] n 18. 2 mm 2, 25% logic utilization, 30 MHz, 65 nm CMOS n CPU time for place & route>10 days 512 Chk & 1024 Var Proc. 384 Chk & 2048 Var Proc. For all data in the plot: n Same automatic place & route flow is used n CPU: Quad Core, Intel Xeon 3. 0 GHz

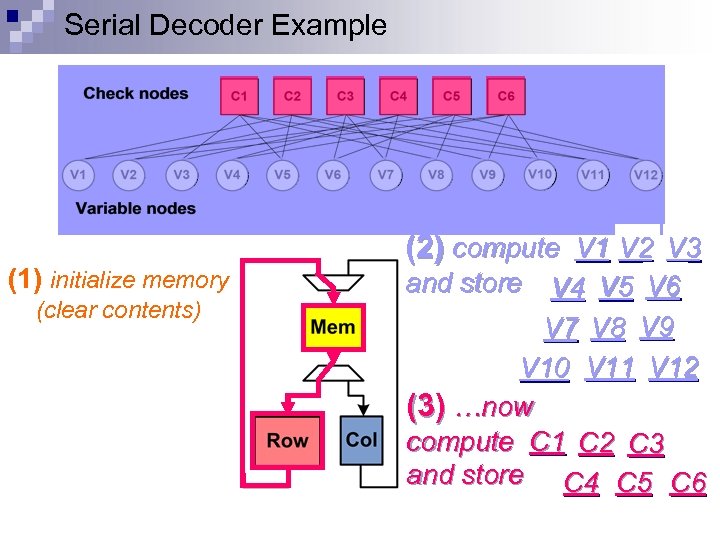Serial Decoder Example (1) initialize memory (clear contents) (2) compute V 1 V 2 V 3 and store V 4 V 5 V 6 V 7 V 8 V 9 V 10 V 11 V 12 (3) …now compute C 1 C 2 C 3 and store C 4 C 5 C 6

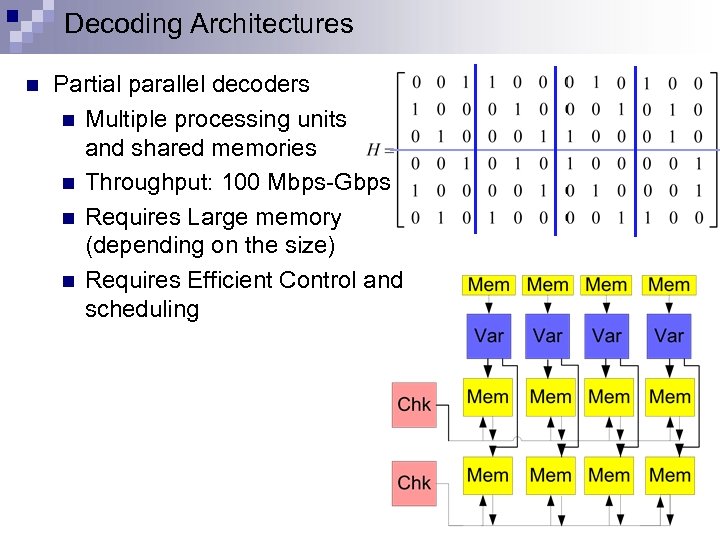Decoding Architectures n Partial parallel decoders n Multiple processing units and shared memories n Throughput: 100 Mbps-Gbps n Requires Large memory (depending on the size) n Requires Efficient Control and scheduling

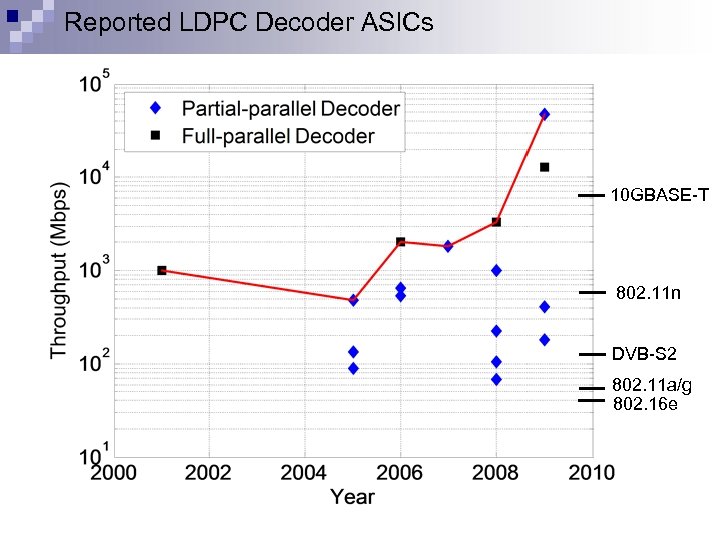Reported LDPC Decoder ASICs 10 GBASE-T 802. 11 n DVB-S 2 802. 11 a/g 802. 16 e

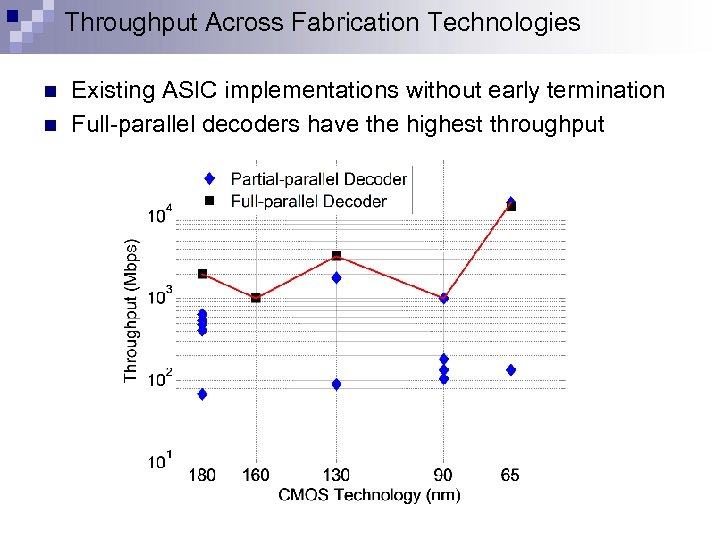Throughput Across Fabrication Technologies n n Existing ASIC implementations without early termination Full-parallel decoders have the highest throughput

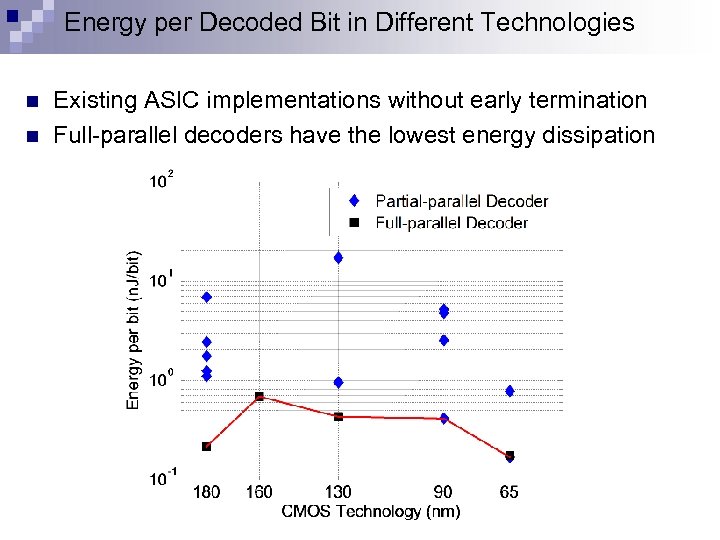Energy per Decoded Bit in Different Technologies n n Existing ASIC implementations without early termination Full-parallel decoders have the lowest energy dissipation

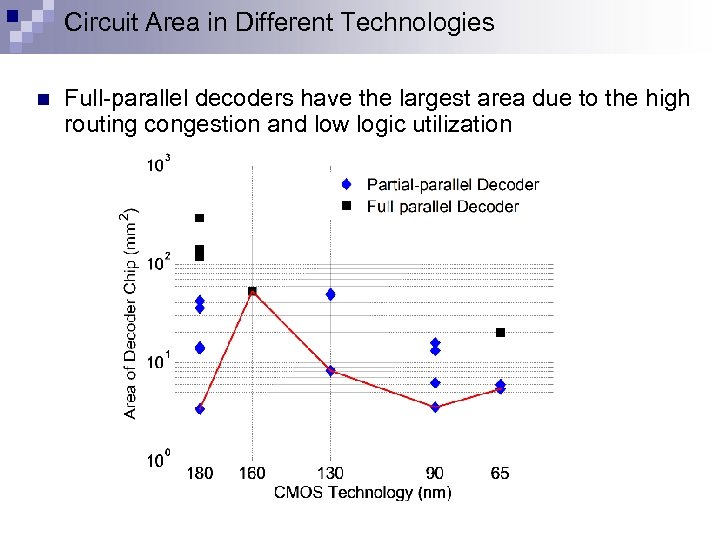Circuit Area in Different Technologies n Full-parallel decoders have the largest area due to the high routing congestion and low logic utilization

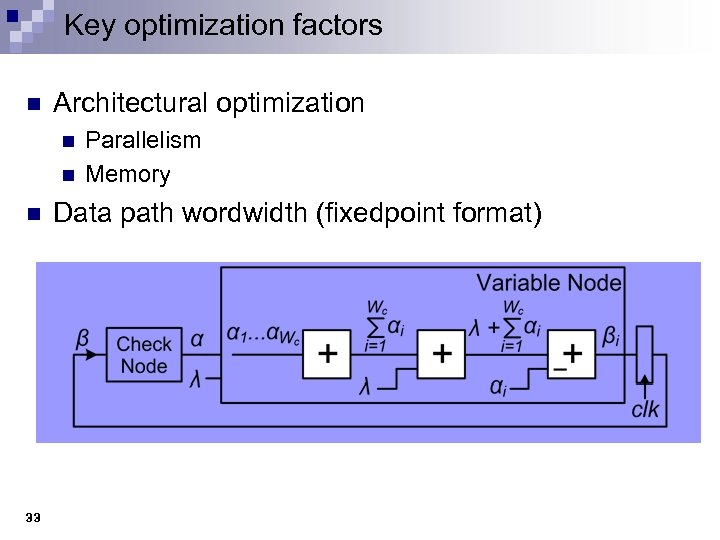Key optimization factors n Architectural optimization n 33 Parallelism Memory Data path wordwidth (fixedpoint format)

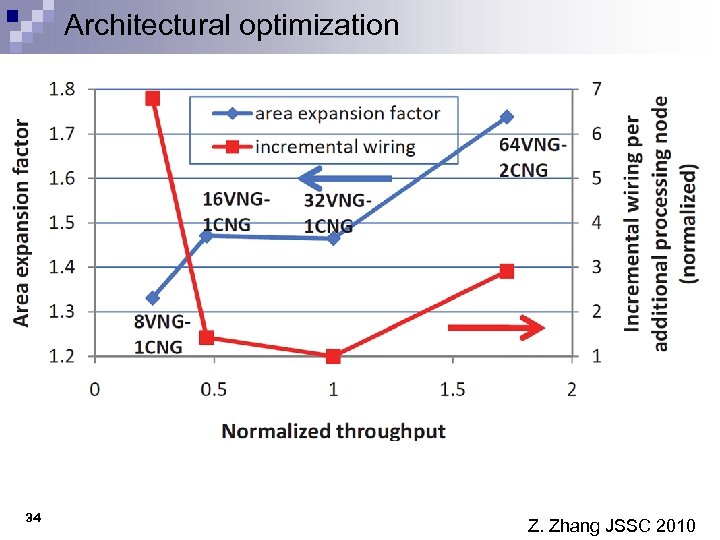Architectural optimization 34 Z. Zhang JSSC 2010

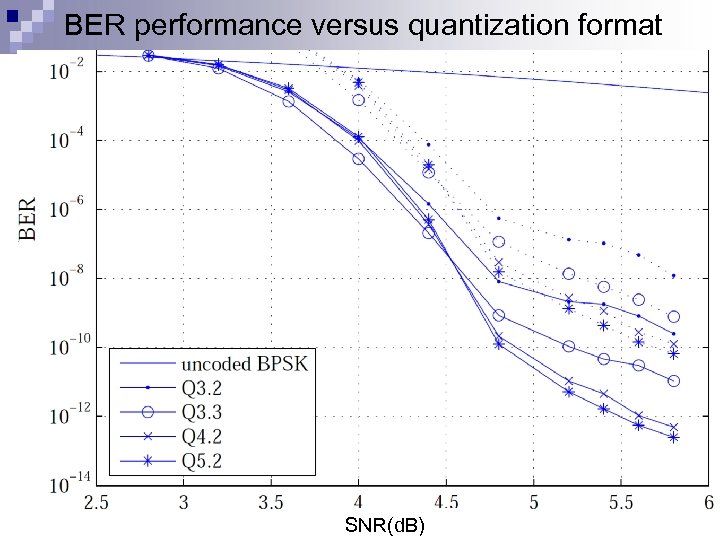BER performance versus quantization format 35 SNR(d. B)

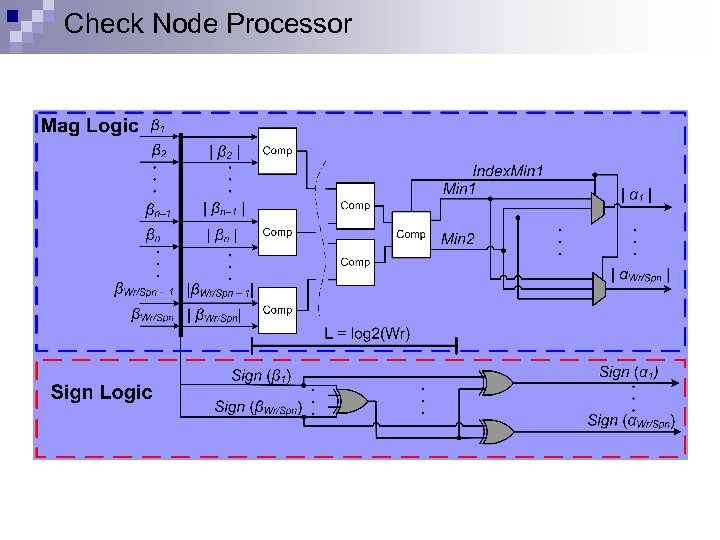Check Node Processor

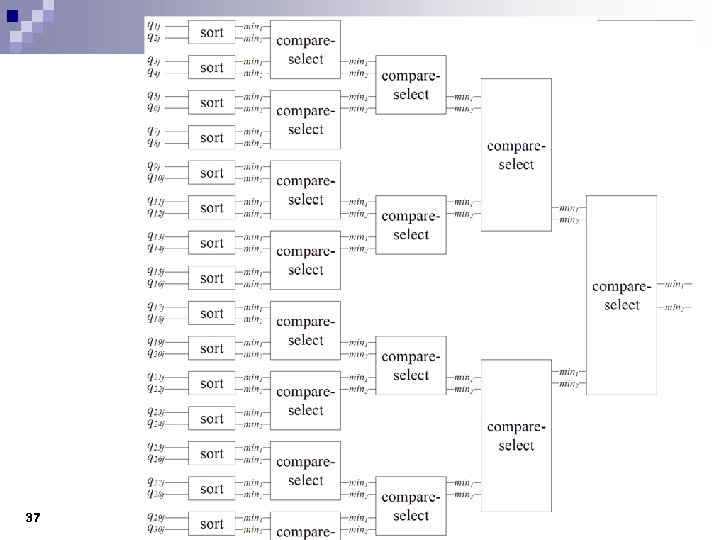37

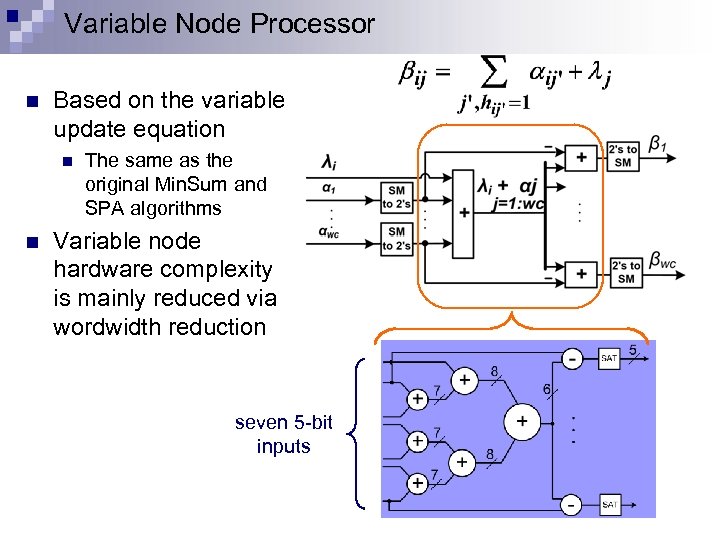Variable Node Processor n Based on the variable update equation n n The same as the original Min. Sum and SPA algorithms Variable node hardware complexity is mainly reduced via wordwidth reduction seven 5 -bit inputs

39

Partial parallel decoder example 40

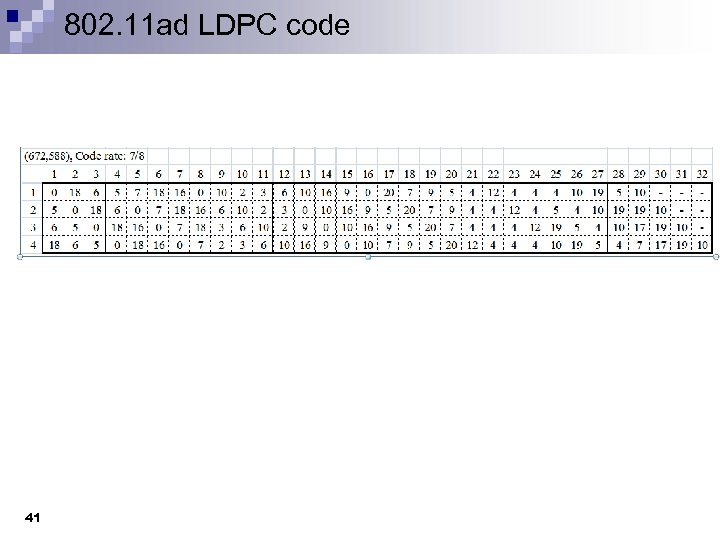802. 11 ad LDPC code 41

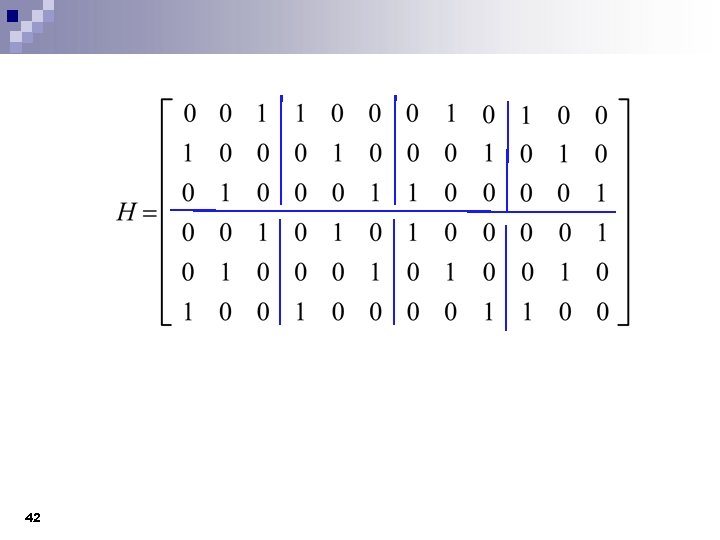42

Transmission scenario 43