bcca5994f0115b660251684840ae012a.ppt
- Количество слайдов: 19
 Error Correction and LDPC decoding 1
Error Correction and LDPC decoding 1
 Error Correction in Communication Systems noise Binary information Transmitter n channel Receiver Corrected information Error: Given the original frame k and the received frame k’, how many corresponding bits differ? n n Hamming distance (Hamming, 1950). Example: n n n 2 frame Corrupted frame Transmitted frame: 1110011 Received frame: 1011001 Number of errors: 3
Error Correction in Communication Systems noise Binary information Transmitter n channel Receiver Corrected information Error: Given the original frame k and the received frame k’, how many corresponding bits differ? n n Hamming distance (Hamming, 1950). Example: n n n 2 frame Corrupted frame Transmitted frame: 1110011 Received frame: 1011001 Number of errors: 3
 Error Detection and Correction n Add extra information to the original data being transmitted. n n Error detection: enough info to detect error. n n Frame = k data bits + m bits for error control: n = k + m. Need retransmissions. Error correction: enough info to detect and correct error. n Forward error correction (FEC). 3
Error Detection and Correction n Add extra information to the original data being transmitted. n n Error detection: enough info to detect error. n n Frame = k data bits + m bits for error control: n = k + m. Need retransmissions. Error correction: enough info to detect and correct error. n Forward error correction (FEC). 3
 Error Correction in Communication Systems Renewed interest in LDPC Introduced 1950 1960 Hamming codes BCH codes 1970 Convolutional codes Reed Solomon codes 1980 1990 2000 Turbo Practical codes implementation LDPC beats of codes Turbo and convolutional codes
Error Correction in Communication Systems Renewed interest in LDPC Introduced 1950 1960 Hamming codes BCH codes 1970 Convolutional codes Reed Solomon codes 1980 1990 2000 Turbo Practical codes implementation LDPC beats of codes Turbo and convolutional codes
 Key terms n n n Encoder : adds redundant bits to the sender's bit stream to create a codeword. Decoder: uses the redundant bits to detect and/or correct as many bit errors as the particular error-control code will allow. Communication Channel: the part of the communication system that introduces errors. n Ex: radio, twisted wire pair, coaxial cable, fiber optic cable, magnetic tape, optical discs, or any other noisy medium n Additive white Gaussian noise (AWGN) n Larger noise makes the distribution wider 5
Key terms n n n Encoder : adds redundant bits to the sender's bit stream to create a codeword. Decoder: uses the redundant bits to detect and/or correct as many bit errors as the particular error-control code will allow. Communication Channel: the part of the communication system that introduces errors. n Ex: radio, twisted wire pair, coaxial cable, fiber optic cable, magnetic tape, optical discs, or any other noisy medium n Additive white Gaussian noise (AWGN) n Larger noise makes the distribution wider 5
 Important metrics n Bit error rate (BER): The probability of bit error. n n We want to keep this number small Ex: BER=10 -4 means if we have transmitted 10, 000 bits, there is 1 bit error. BER is a useful indicator of system performance independent of error channel Signal to noise ratio (SNR): quantifies how much a signal has been corrupted by noise. n defined as the ratio of signal power to the noise power corrupting the signal. A ratio higher than 1: 1 indicates more signal than noise often expressed using the logarithmic decibel scale: n Important number: 3 d. B means signal power is two times noise power n 6
Important metrics n Bit error rate (BER): The probability of bit error. n n We want to keep this number small Ex: BER=10 -4 means if we have transmitted 10, 000 bits, there is 1 bit error. BER is a useful indicator of system performance independent of error channel Signal to noise ratio (SNR): quantifies how much a signal has been corrupted by noise. n defined as the ratio of signal power to the noise power corrupting the signal. A ratio higher than 1: 1 indicates more signal than noise often expressed using the logarithmic decibel scale: n Important number: 3 d. B means signal power is two times noise power n 6
 Error Correction in Communication Systems Information k -bit n n n Goal: Attain lower BER at smaller SNR Error correction is a key component 100 in communication and storage applications. 10 -1 Coding example: Convolutional, Turbo, and Reed-Solomon codes 10 -2 What can 3 d. B of coding gain buy? n n 7 channel Receivedword n-bit A satellite can send data with half the required transmit power A cellphone can operate reliably with half the required receive power Bit Error Probability n Encoder (add parity) Codeword n-bit noise 10 -3 10 -4 Decoder (check parity, detect error) Corrected Information k-bit Uncoded system Convolutional code 0 3 d. B 1 2 3 4 5 6 7 Signal to Noise Ratio (d. B) 8 Figure courtesy of B. Nikolic, 2003 (modified)
Error Correction in Communication Systems Information k -bit n n n Goal: Attain lower BER at smaller SNR Error correction is a key component 100 in communication and storage applications. 10 -1 Coding example: Convolutional, Turbo, and Reed-Solomon codes 10 -2 What can 3 d. B of coding gain buy? n n 7 channel Receivedword n-bit A satellite can send data with half the required transmit power A cellphone can operate reliably with half the required receive power Bit Error Probability n Encoder (add parity) Codeword n-bit noise 10 -3 10 -4 Decoder (check parity, detect error) Corrected Information k-bit Uncoded system Convolutional code 0 3 d. B 1 2 3 4 5 6 7 Signal to Noise Ratio (d. B) 8 Figure courtesy of B. Nikolic, 2003 (modified)
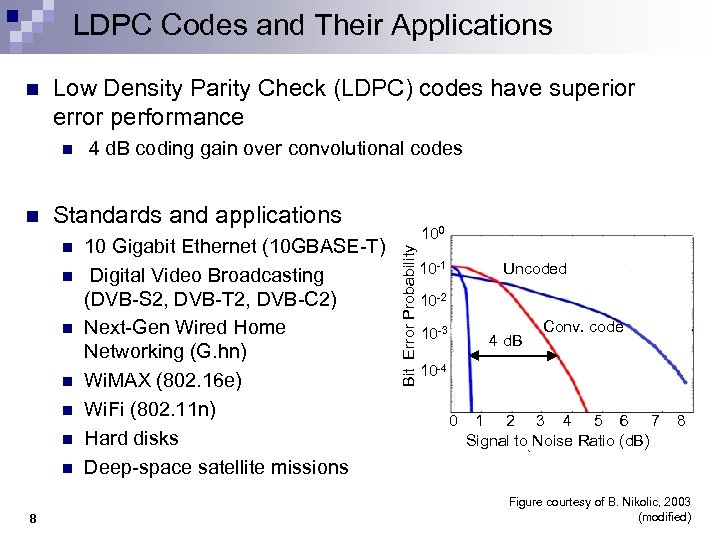 LDPC Codes and Their Applications Low Density Parity Check (LDPC) codes have superior error performance n n Standards and applications n n n n 8 4 d. B coding gain over convolutional codes 10 Gigabit Ethernet (10 GBASE-T) Digital Video Broadcasting (DVB-S 2, DVB-T 2, DVB-C 2) Next-Gen Wired Home Networking (G. hn) Wi. MAX (802. 16 e) Wi. Fi (802. 11 n) Hard disks Deep-space satellite missions 100 Bit Error Probability n Uncoded 10 -1 10 -2 10 -3 4 d. B Conv. code 10 -4 0 1 2 3 4 5 6 7 Signal to Noise Ratio (d. B) 8 Figure courtesy of B. Nikolic, 2003 (modified)
LDPC Codes and Their Applications Low Density Parity Check (LDPC) codes have superior error performance n n Standards and applications n n n n 8 4 d. B coding gain over convolutional codes 10 Gigabit Ethernet (10 GBASE-T) Digital Video Broadcasting (DVB-S 2, DVB-T 2, DVB-C 2) Next-Gen Wired Home Networking (G. hn) Wi. MAX (802. 16 e) Wi. Fi (802. 11 n) Hard disks Deep-space satellite missions 100 Bit Error Probability n Uncoded 10 -1 10 -2 10 -3 4 d. B Conv. code 10 -4 0 1 2 3 4 5 6 7 Signal to Noise Ratio (d. B) 8 Figure courtesy of B. Nikolic, 2003 (modified)
 Future Wireless Devices Requirements n Increased throughput n n n Power budget likely n n Current smart phones require 100 GOPS within 1 Watt [Ref] Required reconfigurability for different environments n n 1 Gbps for next generation of Wi. MAX (802. 16 m) and LTE (Advanced LTE) 2. 2 Gbps Wireless. HD UWB [Ref] A rate-compatible LDPC code is proposed for 802. 16 m [Ref] Required reconfigurability for different communication standards n n Ex: LTE/Wi. Max dual-mode cellphones require Turbo codes (used in LTE) and LDPC codes (used in Wi. MAX) Requires hardware sharing for silicon area saving
Future Wireless Devices Requirements n Increased throughput n n n Power budget likely n n Current smart phones require 100 GOPS within 1 Watt [Ref] Required reconfigurability for different environments n n 1 Gbps for next generation of Wi. MAX (802. 16 m) and LTE (Advanced LTE) 2. 2 Gbps Wireless. HD UWB [Ref] A rate-compatible LDPC code is proposed for 802. 16 m [Ref] Required reconfigurability for different communication standards n n Ex: LTE/Wi. Max dual-mode cellphones require Turbo codes (used in LTE) and LDPC codes (used in Wi. MAX) Requires hardware sharing for silicon area saving
 Future Digital TV Broadcasting Requirements n High definition television for stationery and mobile users n n DTMB/DMB-TH (terrestrial/mobile), ABS-S (satellite), CMMB (multimedia/mobile) Current Digital TV (DTV) standards are not well-suited for mobile devices n n n Require more sophisticated signal processing and correction algorithms Require Low power Require Low error floor n Remove multi-level coding ¨ Recently proposed ABS-S LDPC codes (15, 360 -bit code length, 11 code rates) achieves FER < 10 -7 without concatenation [Ref]
Future Digital TV Broadcasting Requirements n High definition television for stationery and mobile users n n DTMB/DMB-TH (terrestrial/mobile), ABS-S (satellite), CMMB (multimedia/mobile) Current Digital TV (DTV) standards are not well-suited for mobile devices n n n Require more sophisticated signal processing and correction algorithms Require Low power Require Low error floor n Remove multi-level coding ¨ Recently proposed ABS-S LDPC codes (15, 360 -bit code length, 11 code rates) achieves FER < 10 -7 without concatenation [Ref]
 Future Storage Devices Requirements n Ultra high-density storage n 2 Terabit per square inch [ref] n n High throughput n n Worsening Inter. Symbol Interference (ISI) [ref] Larger than 5 Gbps [ref] Low error floor n Lower than 10 -15 [ref] n Remove multi-level coding ¨ Next generation of Hitachi IDRC read-channel technology [9]
Future Storage Devices Requirements n Ultra high-density storage n 2 Terabit per square inch [ref] n n High throughput n n Worsening Inter. Symbol Interference (ISI) [ref] Larger than 5 Gbps [ref] Low error floor n Lower than 10 -15 [ref] n Remove multi-level coding ¨ Next generation of Hitachi IDRC read-channel technology [9]
 Encoding Picture Example V= H×Vi. T=0 Parity Image Binary multiplication called syndrome check
Encoding Picture Example V= H×Vi. T=0 Parity Image Binary multiplication called syndrome check
 Decoding Picture Example Transmitter Receiver noise channel Ethernet cable, Wireless, or Hard disk Iterative message passing decoding Iteration 1 Iteration 5 Iteration 16
Decoding Picture Example Transmitter Receiver noise channel Ethernet cable, Wireless, or Hard disk Iterative message passing decoding Iteration 1 Iteration 5 Iteration 16
 LDPC Codes—Parity Check Matrix n Defined by a large binary matrix, called a parity check matrix or H matrix n n n Example: 6 x 12 H matrix for a 12 -bit LDPC code n n 14 Each row is defined by a parity equation Each parity is generated by a few (not all) information bits No. of columns=12 (i. e. Receivedword (V) = 12 bit) No. of rows= 6 No. of ones per row=3 (row weight) No. of ones per col= 2 (column weight)
LDPC Codes—Parity Check Matrix n Defined by a large binary matrix, called a parity check matrix or H matrix n n n Example: 6 x 12 H matrix for a 12 -bit LDPC code n n 14 Each row is defined by a parity equation Each parity is generated by a few (not all) information bits No. of columns=12 (i. e. Receivedword (V) = 12 bit) No. of rows= 6 No. of ones per row=3 (row weight) No. of ones per col= 2 (column weight)
 LDPC Codes—Tanner Graph n Interconnect representation of H matrix n n Two sets of nodes: Check nodes and Variable nodes Each row of the matrix is represented by a Check node Each column of matrix is represented by a Variable node A message passing method is used between nodes to correct errors (1) Initialization with Receivedword (2) Messages passing until correct Example: V 3 to C 1, V 5 to C 1, V 8 to C 1, V 10 to C 1 C 2 to V 1, C 5 to V 1 Check nodes Variable nodes V 1 15 V 2 V 3 C 1 V 4 C 2 V 5 C 3 V 6 C 4 V 7 C 5 V 8 Receivedword from channel C 6 V 9 V 10 V 11 V 12
LDPC Codes—Tanner Graph n Interconnect representation of H matrix n n Two sets of nodes: Check nodes and Variable nodes Each row of the matrix is represented by a Check node Each column of matrix is represented by a Variable node A message passing method is used between nodes to correct errors (1) Initialization with Receivedword (2) Messages passing until correct Example: V 3 to C 1, V 5 to C 1, V 8 to C 1, V 10 to C 1 C 2 to V 1, C 5 to V 1 Check nodes Variable nodes V 1 15 V 2 V 3 C 1 V 4 C 2 V 5 C 3 V 6 C 4 V 7 C 5 V 8 Receivedword from channel C 6 V 9 V 10 V 11 V 12
 Message Passing: Variable node processing α: message from check to variable node β: message from variable to check node 16 λ is the original received information from the channel
Message Passing: Variable node processing α: message from check to variable node β: message from variable to check node 16 λ is the original received information from the channel
 Message Passing: Check node processing (Min. Sum) After check node processing, the next iteration starts with another variable node processing (begins a new iteration) Sign 17 Magnitude
Message Passing: Check node processing (Min. Sum) After check node processing, the next iteration starts with another variable node processing (begins a new iteration) Sign 17 Magnitude
![Example Encoded information V= [1 0 1 0 1 1 1 1] BPSK modulated= Example Encoded information V= [1 0 1 0 1 1 1 1] BPSK modulated=](https://present5.com/presentation/bcca5994f0115b660251684840ae012a/image-18.jpg) Example Encoded information V= [1 0 1 0 1 1 1 1] BPSK modulated= [-1 1 -1 -1] λ (Received data from channel)= [ -9. 1 4. 9 -3. 2 3. 6 -1. 4 3. 1 0. 3 1. 6 -6. 1 -2. 5 -7. 8 -6. 8] Estimated code= ^ V= 1 0 1 18 0 1 0 0 0 1 1
Example Encoded information V= [1 0 1 0 1 1 1 1] BPSK modulated= [-1 1 -1 -1] λ (Received data from channel)= [ -9. 1 4. 9 -3. 2 3. 6 -1. 4 3. 1 0. 3 1. 6 -6. 1 -2. 5 -7. 8 -6. 8] Estimated code= ^ V= 1 0 1 18 0 1 0 0 0 1 1
 Syndrome computation Step 1: syndrome check: H. Vt=0? Estimated code= ^ V= 1 0 1 Syndrome = [0 19 0 1 0] Sumsyndrome=2 Not ZERO then Error 1 1 1
Syndrome computation Step 1: syndrome check: H. Vt=0? Estimated code= ^ V= 1 0 1 Syndrome = [0 19 0 1 0] Sumsyndrome=2 Not ZERO then Error 1 1 1


