LlectureNo2_on_Physics_1.pptx
- Количество слайдов: 42

Error Analysis arithmetic mean

Error Analysis absolute error and relative error

Error Analysis Standard deviation .
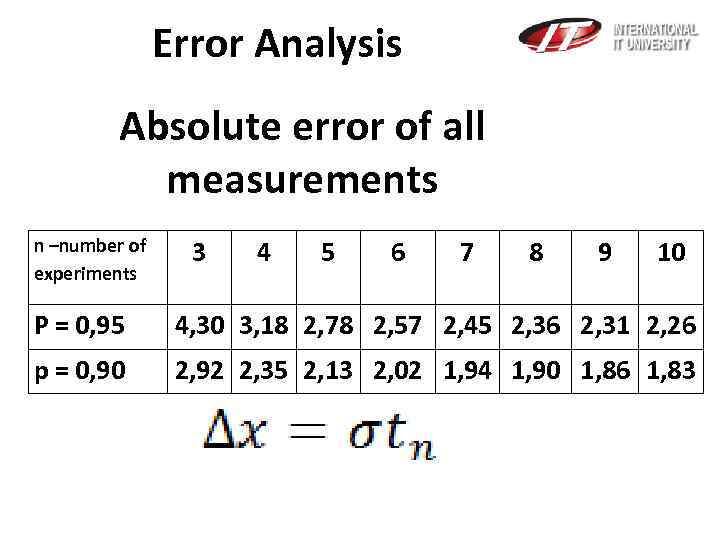
Error Analysis Absolute error of all measurements n –number of experiments 3 4 5 6 7 8 9 10 Р = 0, 95 4, 30 3, 18 2, 78 2, 57 2, 45 2, 36 2, 31 2, 26 p = 0, 90 2, 92 2, 35 2, 13 2, 02 1, 94 1, 90 1, 86 1, 83

Error Analysis Significant figures A common convention in science and engineering is to express accuracy and/or precision implicitly by means of significant figures. The margin of error is understood to be one-half the value of the last significant place. For instance, a recording of 843. 6 m, or 843. 0 m, or 800. 0 m would imply a margin of 0. 05 m (the last significant place is the tenths place), while a recording of 8, 436 m would imply a margin of error of 0. 5 m (the last significant digits are the units).

Error Analysis Significant figures A reading of 8, 000 m, with trailing zeroes and no decimal point, is ambiguous; the trailing zeroes may or may not be intended as significant figures. To avoid this ambiguity, the number could be represented in scientific notation: 8. 0 × 103 m indicates that the first zero is significant (hence a margin of 50 m) while 8. 000 × 103 m indicates that all three zeroes are significant, giving a margin of 0. 5 m. Similarly, it is possible to use a multiple of the basic measurement unit: 8. 0 km is equivalent to 8. 0 × 10 3 m. In fact, it indicates a margin of 0. 05 km (50 m).

Error Analysis Significant figures 8 × 8 = 6 × 101 8 × 8. 0 = 6 × 101 8. 0 × 8. 0 = 64 8. 02 × 8. 02 = 64. 3 8 / 2. 0 = 4 8. 6 /2. 0012 = 4. 3 2 × 0. 8 = 2 If, in the above, the numbers are assumed to be measurements (and therefore probably inexact) then "8" above represents an inexact measurement with only one significant digit. Therefore, the result of "8 × 8" is rounded to a result with only one significant digit, i. e. , "6 × 101" instead of the unrounded "64" that one might expect. In many cases, the rounded result is less accurate than the nonrounded result; a measurement of "8" has an actual underlying quantity between 7. 5 and 8. 5.

Error Analysis Significant figures Addition and subtraction using significance arithmetic • 1 + 1. 1 = 2 1 is significant to the ones place, 1. 1 is significant to the tenths place. Of the two, the least accurate is the ones place. The answer cannot have any significant figures past the ones place. • 1. 0 + 1. 1 = 2. 1 1. 0 and 1. 1 are significant to the tenths place, so the answer will also have a number in the tenths place. • 100 + 110 = 200 100 is significant to the hundreds place, while 110 is significant to the tens place. Therefore, the answer must be rounded to the nearest hundred. • 100. + 110. = 210. 100. and 110. are both significant to the ones place (as indicated by the decimal), so the answer is also significant to the ones place. • 1× + 1. 1× = 2× 100 is significant up to the hundreds place, while 110 is up to the tens place. Of the two, the least accurate is the hundreds place. The answer should not have significant digits past the hundreds place.

Frame of reference All inertial frames share a universal time A frame of reference in physics, may refer to a coodinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer. It may also refer to both an observational reference frame and an attached coordinate system, as a unit.
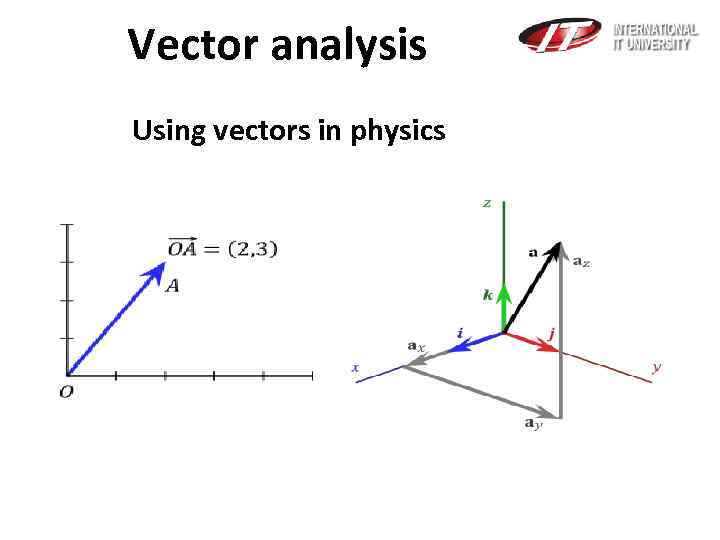
Vector analysis Using vectors in physics

Vector analysis Dot product The dot product of two vectors a and b (sometimes called the inner product, or, since its result is a scalar, the scalar product) is denoted by a ∙ b and is defined as: where θ is the measure of the angle between a and b. Geometrically, this means that a and b are drawn with a common start point and then the length of a is multiplied with the length of that component of b that points in the same direction as a.
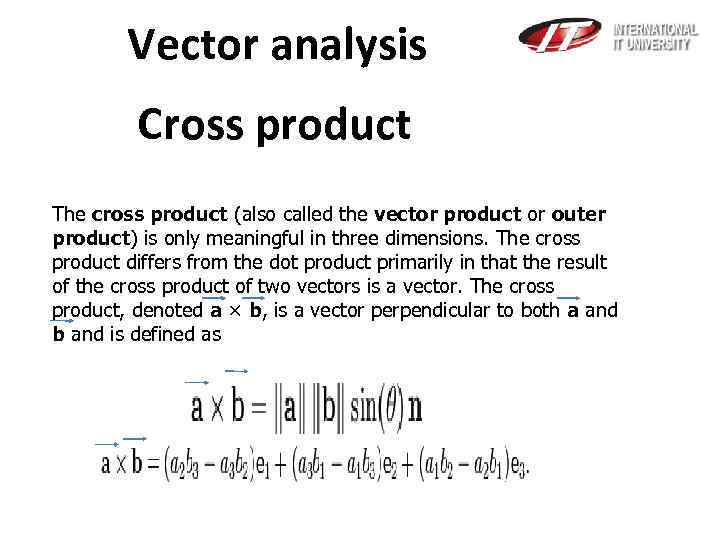
Vector analysis Cross product The cross product (also called the vector product or outer product) is only meaningful in three dimensions. The cross product differs from the dot product primarily in that the result of the cross product of two vectors is a vector. The cross product, denoted a × b, is a vector perpendicular to both a and b and is defined as

Vector analysis Combinations of multiple operators

Vector analysis Divergence of a vector field

Vector analysis Curl of a vector field

Vector analysis Using vectors in physics Velocity is defined as the rate of change of position with respect to time. You may be used to writing velocity, v, as a scalar because it was assumed in your solution that v referred to speed in the direction of travel. However, if we take the strict definition and apply it to the position vector - which we have already established is the proper way of representing position - we get:
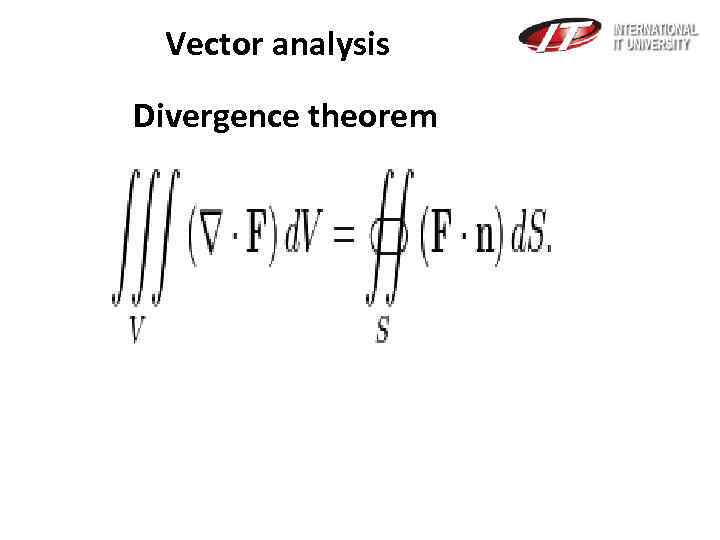
Vector analysis Divergence theorem

Vector analysis Stock’s theorem

1. Stock’s theorem y x

Contemporary Physics: Part 1 Lecture № 2 Laws of Motion Time . Currently, the standard time interval (called conventional second, or simply second) is defined as 9 192 631 770 oscillations of a hyperfine transition in the 133 caesium atom.

Length In the physical sciences and engineering, when one speaks of "units of length", the word "length" is synonymous with distance. In the International System of Units(SI), the basic unit of length is the meter and is now defined in terms of the speed of light. The centimeter and the kilometer, derived from the meter, are also commonly used units. Units used to denote distances in the vastness of space, as in astronomy, are much longer than those typically used on Earth and include the astronomical unit, the light year

Mass is the internal property of the matter and shows its resistance to change its speed. Mass, in physics, the quantity of matter in a body regardless of its volume or of any forces acting on it. The term should not be confused with weight, which is the measure of the force of gravity acting on a body. Under ordinary conditions the mass of a body can be considered to be constant; its weight, however, is not constant, since the force of gravity varies from place to place. Because the numerical value for the mass of a body is the same anywhere in the world, it is used as a basis of reference for many physical measurements, such as density and heat capacity. The SI unit of mass is kilograms.

Inertia is the resistance of any physical object to a change in its state of motion or rest. It is represented numerically by an object's mass

Velocity Instantaneous velocity The instantaneous velocity vector v of an object that has positions r(t) at time t and r(t + Δ t) at time t + Δ t , can be computed as the derivate of position:

Velocity vector It can be seen that the rate of change of the angular position of the particle is related to the cross-radial velocity by Utilizing θ, the angle between vectors v∥ and v, or equivalently as the angle between vectors r and v, gives: Combining the above two equations and defining the angular velocity as ω=dΦ/dt yields:

Force A a force is any influence that causes a free body to undergo an accelletion. Force can also be described by intuitive concepts such as a push or pull that can cause an object with mass to change its velocity (which includes to begin moving from a state of rest), i. e. , to accelerate, or which can cause a flexible object to deform. A force has both magnitude and direction, making it a vector quantity. Newton’s second law: F=ma, can be formulated to state that an object with a constant mass will accelerate in proportion to the net force acting upon and in inverse proportion to its mass, an approximation which breaks down near the speed of light. Newton's original formulation is exact, and does not break down: this version states that the net force acting upon an object is equal to the rate at which its momentum changes

Force A modern statement of Newton's second law is a vector differential equation:

Force Linear momentum of a closed system is conserved This means that in a closed system of particles, there are no internal forces that are unbalanced. That is, action-and-reaction pairs of forces shared between any two objects in a closed system will not cause the center of mass of the system to accelerate. The constituent objects only accelerate with respect to each other, the system itself remains unaccelerated. Alternatively, if an external force acts on the system, then the center of mass will experience an acceleration proportional to the magnitude of the external force divided by the mass of the system. [Combining Newton's second and third laws, it is possible to show that the linear momentum of a system is conserved.

1. Gravitational Force Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is directly proportional to the product of the two masses and inversely proportional to the square of the distance between the point masses: where: F is the magnitude of the gravitational force between the two point masses, G is the gravitational constant, m 1 is the mass of the first point mass, m 2 is the mass of the second point mass, and r is the distance between the two point masses.

Gravitational Force Assuming SI units , F is measured in newtons (N), m 1 and m 2 in kilograms (kg), r in meters (m), and the constant G is approximately equal to 6. 674× 10− 11 N m 2 kg− 2

Gravitational field The gravitational field is a vector field that describes the gravitational force which would be applied on an object in any given point in space, per unit mass. It is actually equal to the gravitational acceleration at that point. It is a generalization of the vector form, which becomes particularly useful if more than 2 objects are involved (such as a rocket between the Earth and the Moon). For 2 objects (e. g. object 2 is a rocket, object 1 the Earth), we simply write r instead of r 12 and m instead of m 2 and define the gravitational field g(r) as:

Gravitational field Gravitational potential Gravitational fields are also conservative; that is, the work done by gravity from one position to another is path-independent. This has the consequence that there exists a gravitational potential field V(r) such that

Gravitational field Gravitational potential Gravitational fields are also conservative; that is, the work done by gravity from one position to another is path-independent. This has the consequence that there exists a gravitational potential field V(r) such that

Electrostatic Force Coulomb’s law resembles Gravitation law

Electrostatic Force Electric charge internal matter property Electric charge is a physical property of matter which causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive forces, as do two negatively charged objects. Positively charged objects and negatively charged objects experience an attractive force. The SI unit of quantity of electric charge is the coulomb, which is equivalent to about 6. 242× 1018 e (e is the charge of a proton). Hence, the charge of an electron is approximately − 1. 602× 10− 19 C. The coulomb is defined as the quantity of charge that has passed through the cross section of an electrical conductor carrying 6. 242× 1018 electrones within one second.

Similarities between electrostatic and gravitational forces • Both act in a vacuum. • Both are central and conservative. • Both obey an inverse-square law (both are inversely proportional to square of r). • Both propagate with finite speed c.

Electrostatic forces are much greater than gravitational forces (by about 1036 times). Around 6. 241 × 1018 electrons passing a given point each second constitutes one ampere. There are no negative gravitational charges (no negative mass) while there are both positive and negative electric charges. This difference combined with previous implies that gravitational forces are always attractive, while electrostatic forces may be either attractive or repulsive.

Differences between electrostatic and gravitational forces 1. Electrostatic forces are much greater than gravitational forces (by about 1036 times). 2. Gravitational forces are attractive for any mass, whereas electrostatic forces are repulsive for like charges. 3. There are no negative gravitational charges (no negative mass) while there are both positive and negative electric charges. This difference combined with previous implies that gravitational forces are always attractive, while electrostatic forces may be either attractive or repulsive 4. Electric charge is conserved while relativistic mass is not y v

The Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields where F is the force (in newtons) E is the electric field (in volts per metre) B is the magnetic field (in teslas) q is the electric charge of the particle (in coulombs) v is the instantaneous velocity of the particle (in metres per second) × is the vector cross product

Quiz 1. 2. 3. 4. 5. Arithmetic mean of the following 1, 2, 3, 2 numbers is: 2 8 10 12 3

Quiz Absolute error and standard deviation are in the following relation:

Quiz
LlectureNo2_on_Physics_1.pptx