4862303c3e5a9e7b89844abfcb8a06f2.ppt
- Количество слайдов: 37

Equivalences on Labelled Transition Systems Ed Brinksma Course 2004
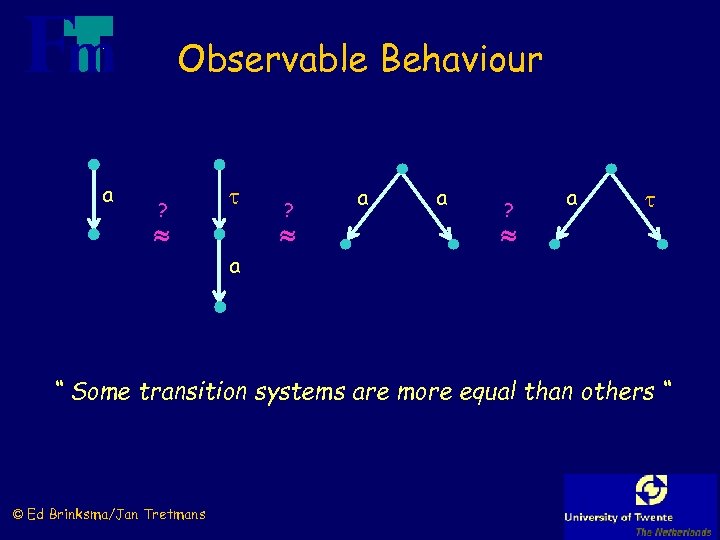
Observable Behaviour a ? a a ? a “ Some transition systems are more equal than others “ © Ed Brinksma/Jan Tretmans
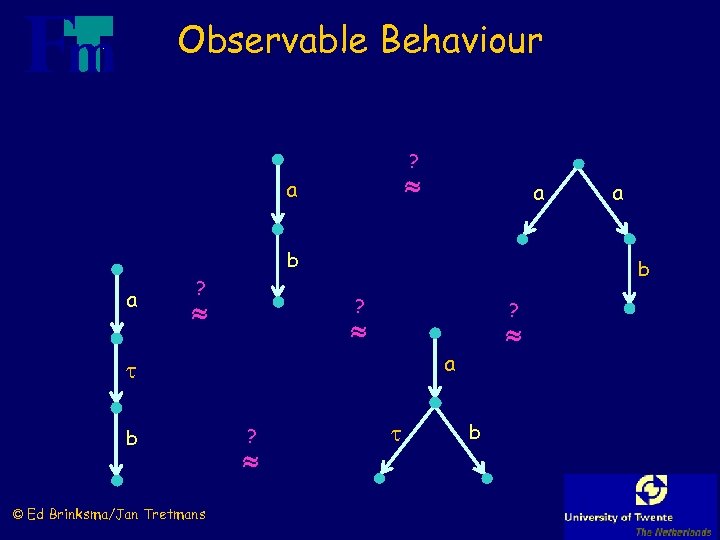
Observable Behaviour ? a a b a ? b ? ? © Ed Brinksma/Jan Tretmans a b ? a b

Isomorphism: p q bijection : Sp Sq : s 1, s 2 S p , L { } : s 1 "p and q are exactly the same modulo state names" s 0 a s 2 (s 1) s 1 © Ed Brinksma/Jan Tretmans v (s 2) (s 0 p) = s 0 q u a a
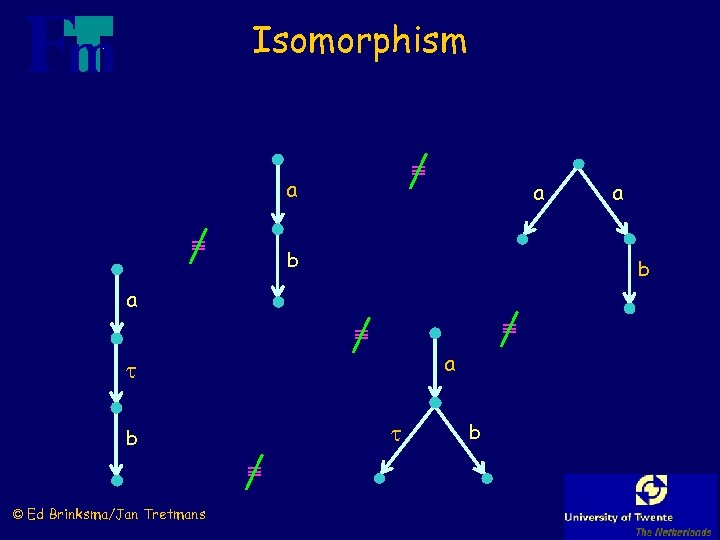
Isomorphism a a b b a a b © Ed Brinksma/Jan Tretmans a b
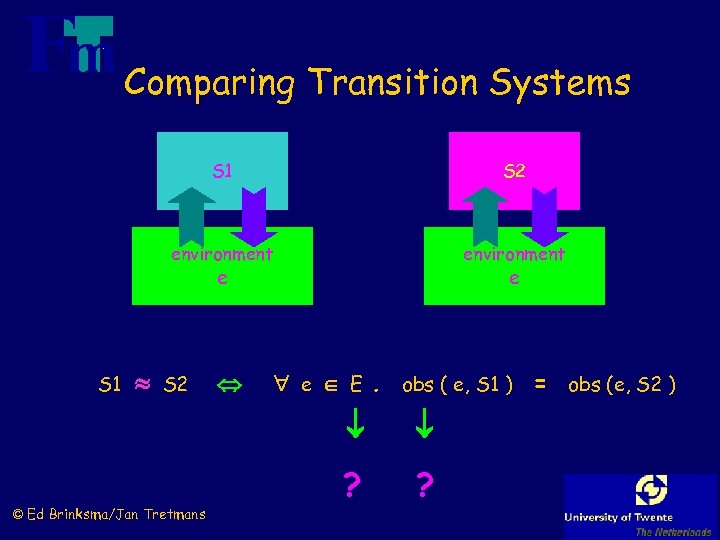
Comparing Transition Systems S 1 S 2 environment e S 1 S 2 e e E. obs ( e, S 1 ) = obs (e, S 2 ) © Ed Brinksma/Jan Tretmans ? ?
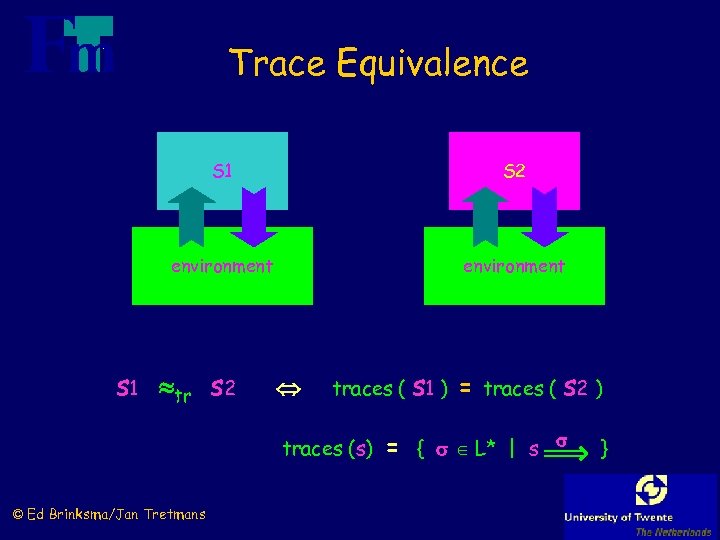
Trace Equivalence S 1 S 2 environment s 1 tr s 2 traces ( s 1 ) traces (s) © Ed Brinksma/Jan Tretmans = traces ( s 2 ) = { L* | s }
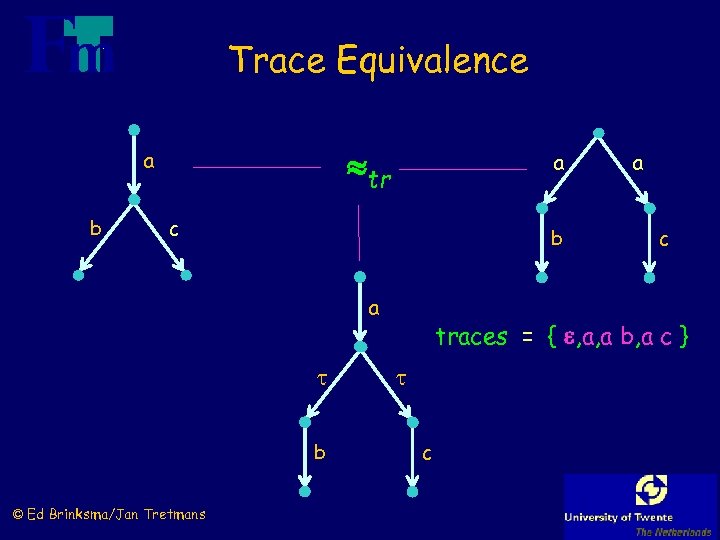
Trace Equivalence tr a b a c b a b © Ed Brinksma/Jan Tretmans a c traces = { , a, a b, a c } c

Completed Trace Equivalence = { L* | s Traces: traces (s) Trace equivalence: p tr q traces(p) = traces (q) Reachable states: s after = { s’ | s Refusal: s refuses A Refusals: } s’ } a A: s after refuses A s' s after : s' refuses A Ctraces (s) = { L* | s after refuses L } Completed traces: Completed trace equivalence: © Ed Brinksma/Jan Tretmans p ctr q Ctraces(p) = Ctraces (q) and traces(p) = traces (q)
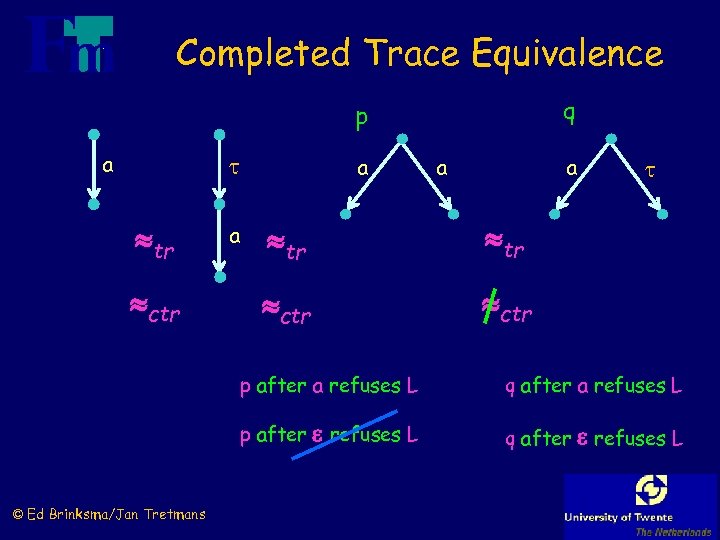
Completed Trace Equivalence q p a tr ctr a a a tr ctr p after a refuses L p after © Ed Brinksma/Jan Tretmans a refuses L q after a refuses L q after refuses L
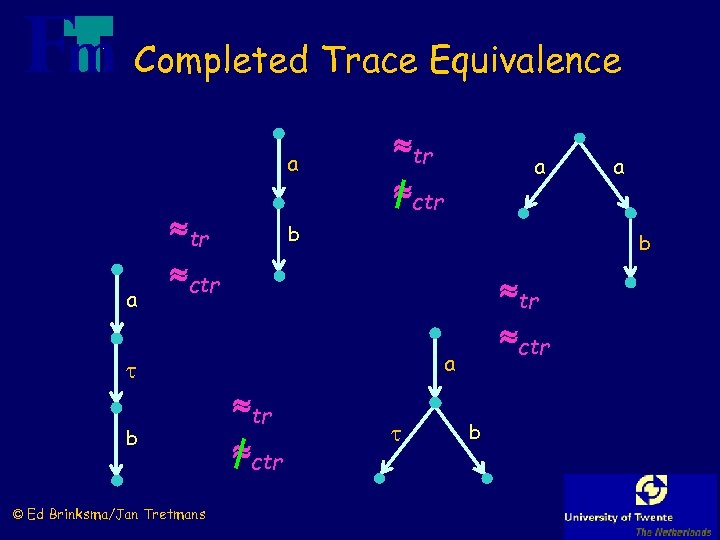
Completed Trace Equivalence a a tr ctr b © Ed Brinksma/Jan Tretmans tr ctr a b b tr ctr a b
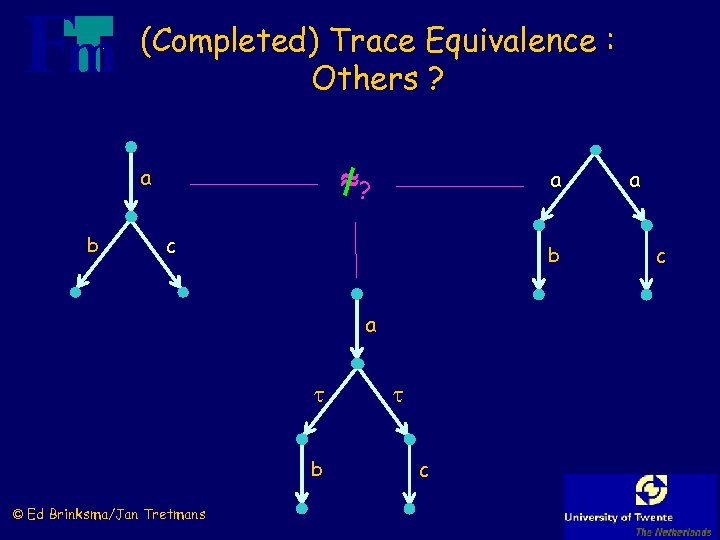
(Completed) Trace Equivalence : Others ? ? a b a c b a b © Ed Brinksma/Jan Tretmans c a c
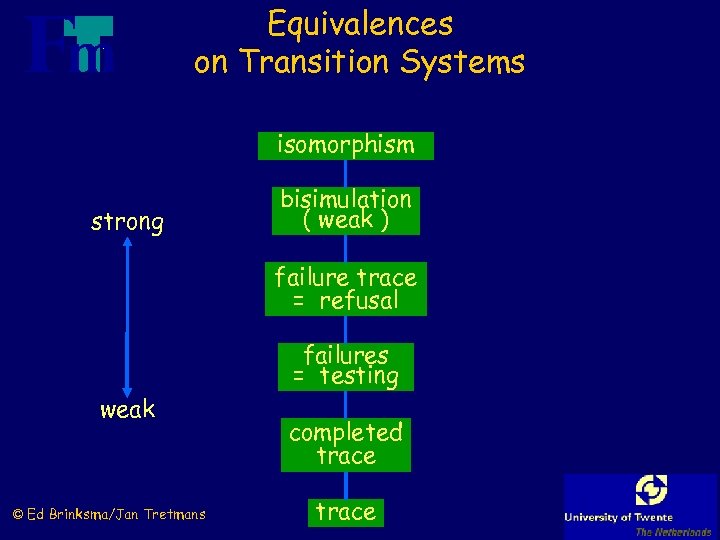
Equivalences on Transition Systems isomorphism strong bisimulation ( weak ) failure trace = refusal failures = testing weak © Ed Brinksma/Jan Tretmans completed trace
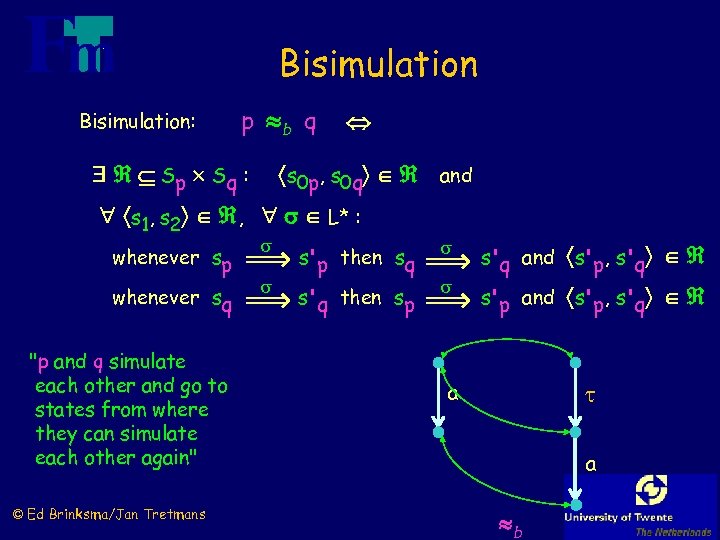
Bisimulation: p b q Sp Sq : s 0 p, s 0 q and s 1, s 2 , L* : whenever sp whenever sq "p and q simulate each other and go to states from where they can simulate each other again" © Ed Brinksma/Jan Tretmans s'p then sq s'q then sp s'q and s'p, s'q s'p and s'p, s'q a a b
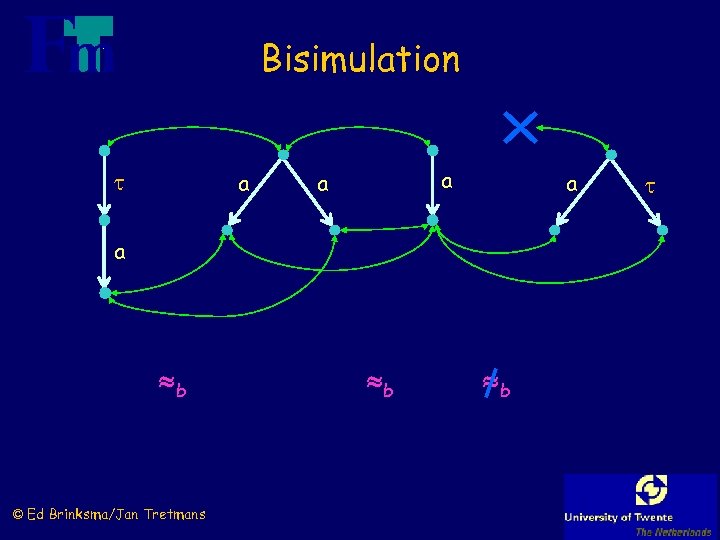
Bisimulation a a a b © Ed Brinksma/Jan Tretmans b b
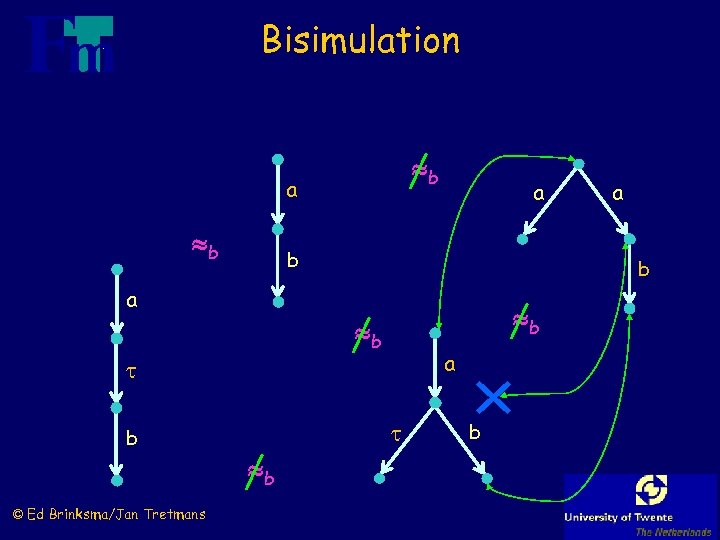
Bisimulation b a b b a b © Ed Brinksma/Jan Tretmans b a b
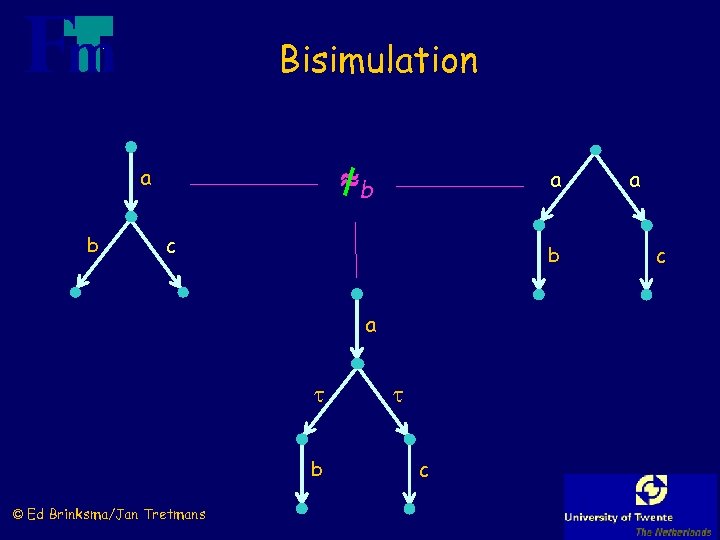
Bisimulation b a c b a b © Ed Brinksma/Jan Tretmans c a c

Comparing Systems : Testing Equivalence S 1 environment S 1 S 2 environment te S 2 e E. obs ( e, S 1 ) = obs (e, S 2 ) ? ? LTS(L) Ctraces (e||s) © Ed Brinksma/Jan Tretmans

Testing Equivalence S 1 environment S 1 S 2 environment te S 2 e LTS(L). L*. e||S 1 after refuses L e||S 2 after refuses L © Ed Brinksma/Jan Tretmans
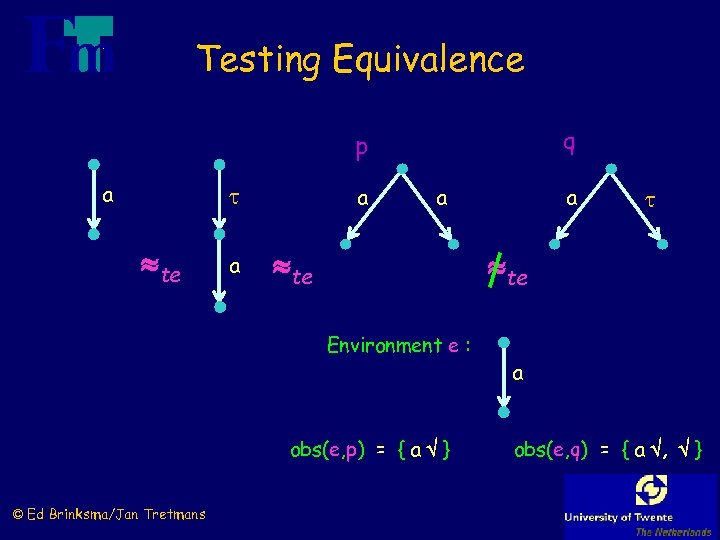
Testing Equivalence q p a te a a a te te Environment e : obs(e, p) = { a } © Ed Brinksma/Jan Tretmans a a obs(e, q) = { a , }
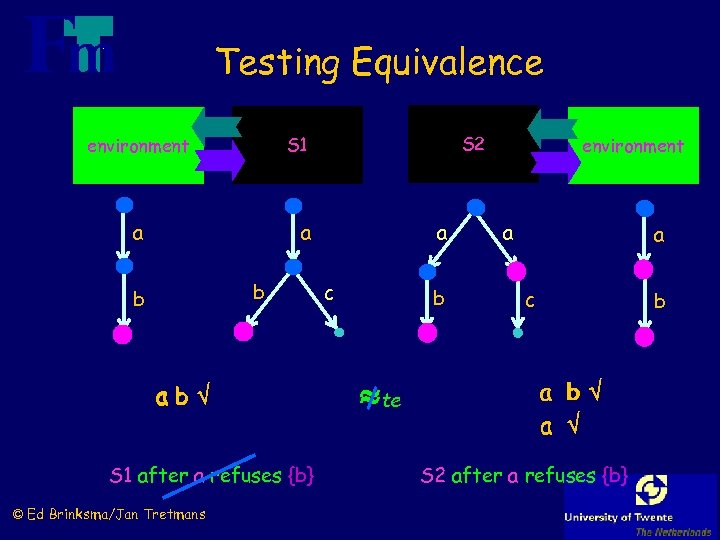
Testing Equivalence S 2 S 1 environment a a b b ab S 1 after a refuses {b} © Ed Brinksma/Jan Tretmans a c b te environment a a c b a S 2 after a refuses {b}

Testing Equivalence Failure pairs of p : = { , A | A L, traces(p), FP (p) p afer refuses A } Failure equivalence = testing equivalence : a FP a P : te q FP(p) = FP(q) Not FP : a , {c} c © Ed Brinksma/Jan Tretmans ab, L aa, , b a , {b, c} , L
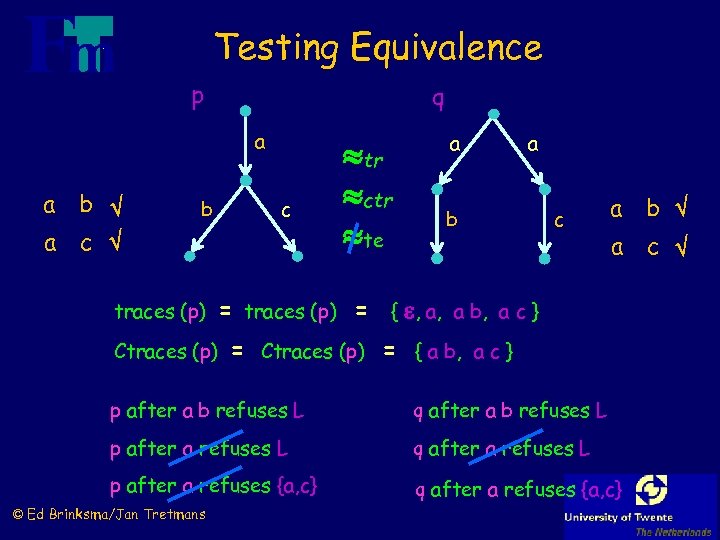
Testing Equivalence p q a a b a c b traces (p) c tr ctr te a a b c a b a c = traces (p) = { , a, a b, a c } Ctraces (p) = { a b, a c } p after a b refuses L q after a b refuses L p after a refuses L q after a refuses L p after a refuses {a, c} q after a refuses {a, c} © Ed Brinksma/Jan Tretmans
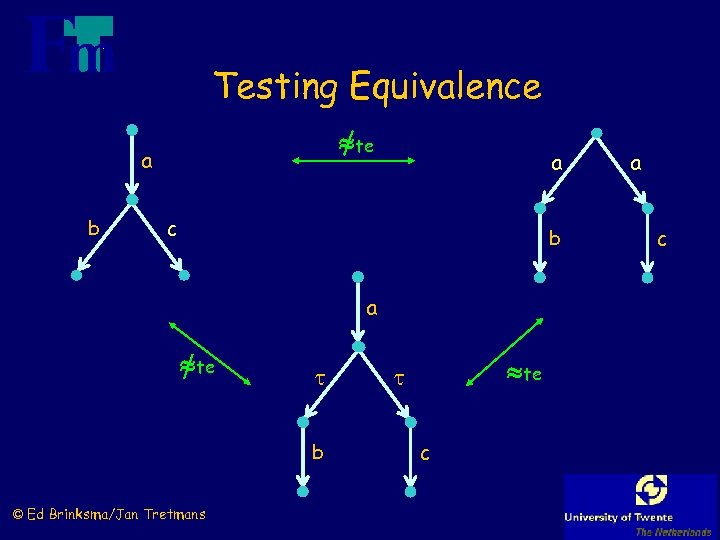
Testing Equivalence te a b a c b a te b © Ed Brinksma/Jan Tretmans te c a c
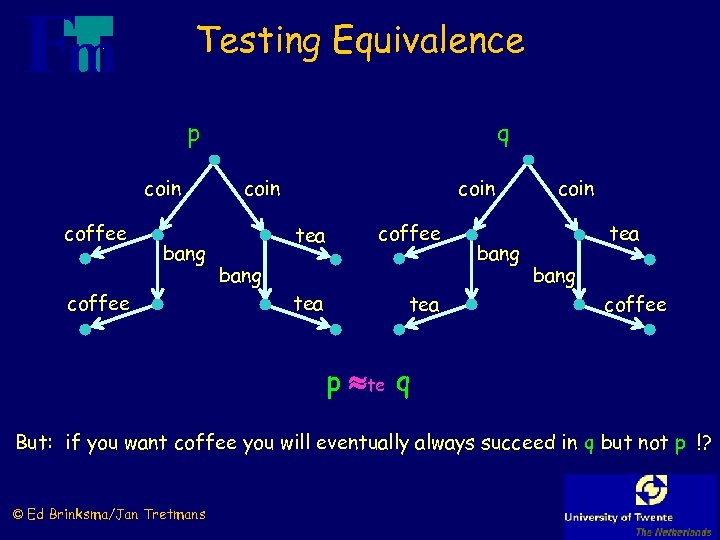
Testing Equivalence p coin coffee bang coffee q coin tea bang tea coffee tea bang coin tea bang coffee p te q But: if you want coffee you will eventually always succeed in q but not p !? © Ed Brinksma/Jan Tretmans
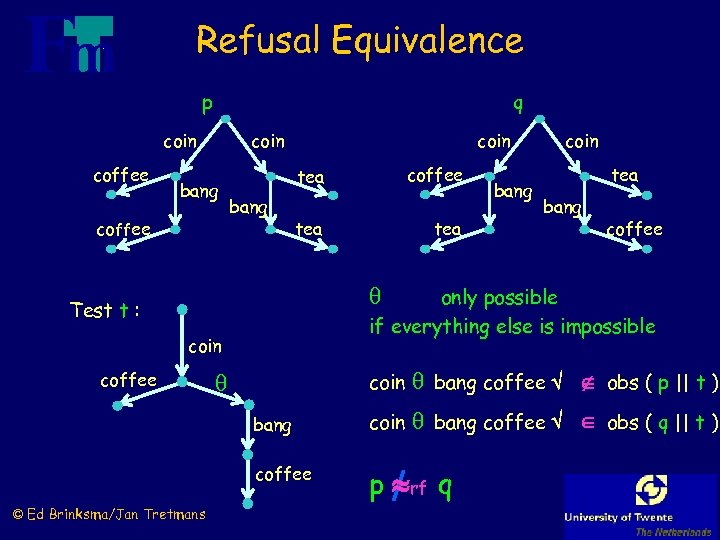
Refusal Equivalence p q coin coffee coin bang coffee coin coffee tea bang coin tea bang coffee only possible if everything else is impossible Test t : coin bang coffee obs ( p || t ) coin bang coffee obs ( q || t ) coffee © Ed Brinksma/Jan Tretmans coin bang coffee p rf q
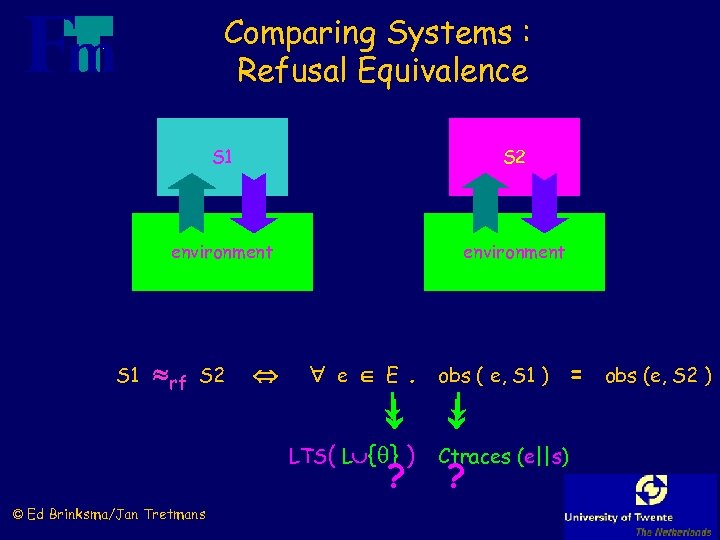
Comparing Systems : Refusal Equivalence S 1 environment S 1 S 2 environment rf S 2 e E. obs ( e, S 1 ) = obs (e, S 2 ) LTS( L { } ? © Ed Brinksma/Jan Tretmans ) Ctraces (e||s) ?

Refusal Equivalence S 1 environment S 1 S 2 environment rf S 2 e LTS(L { }). L*. e||S 1 after refuses L e||S 2 after refuses L © Ed Brinksma/Jan Tretmans

Refusal Equivalence Failure A: s Failure trace : A s Failure trace equivalence = refusal equivalence : Ftraces a P = { ( L ) )* | p rf q : A { }: s ( L ) )* : s Failure traces of p : Ftraces (p) a Ftraces(p) = Ftraces (q) Not Ftraces : {b, c} a {a, c} b L c © Ed Brinksma/Jan Tretmans a {c} b {a} {b} {c} a {c} c L a {b} c b {a, b, c} a {a, c} b L a a }
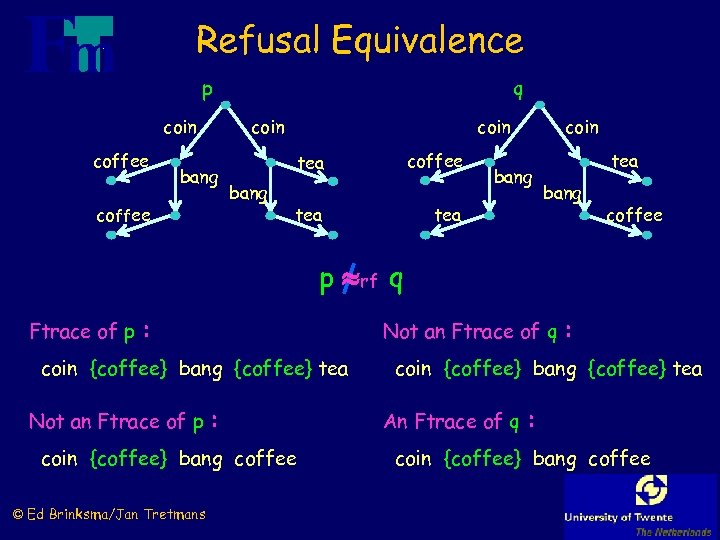
Refusal Equivalence p coin coffee bang coffee q coin coffee tea bang tea coin tea bang coffee p rf q Ftrace of p : coin {coffee} bang {coffee} tea Not an Ftrace of p : coin {coffee} bang coffee © Ed Brinksma/Jan Tretmans Not an Ftrace of q : coin {coffee} bang {coffee} tea An Ftrace of q : coin {coffee} bang coffee

Equivalences on Transition Systems isomorphism weak bisimulation ( weak ) test an LTS with another LTS, and undo, copy, repeat as often as you like failure trace = refusal strong now you need to observe 's …… test an LTS with another LTS, and try again (continue) after failures = testing test an LTS with another LTS completed trace observing sequences of actions and their end trace © Ed Brinksma/Jan Tretmans observing sequences of actions
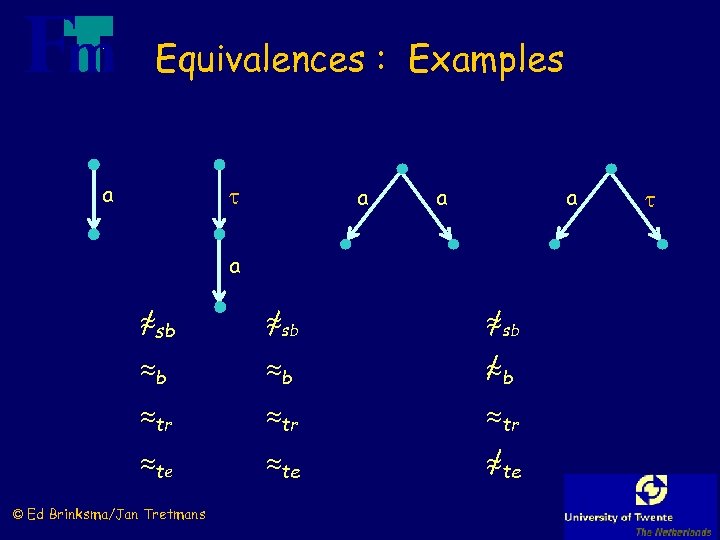
Equivalences : Examples a a a sb sb b tr tr te te © Ed Brinksma/Jan Tretmans
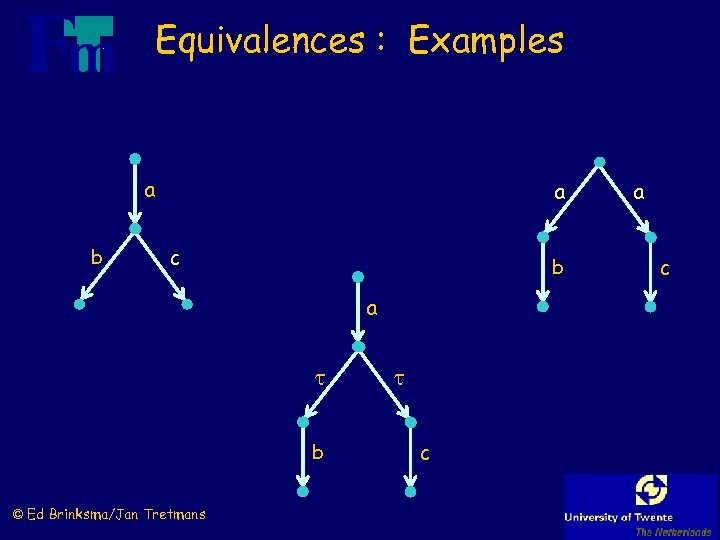
Equivalences : Examples a b a c b a b © Ed Brinksma/Jan Tretmans c a c
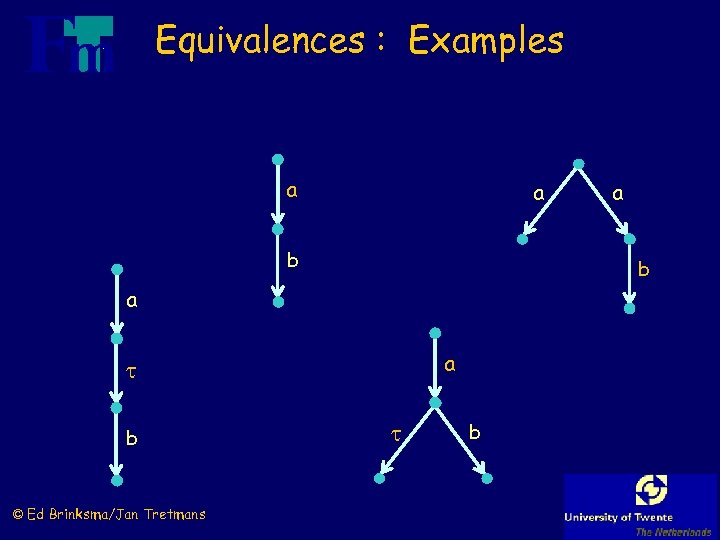
Equivalences : Examples a a b b a a b © Ed Brinksma/Jan Tretmans a b
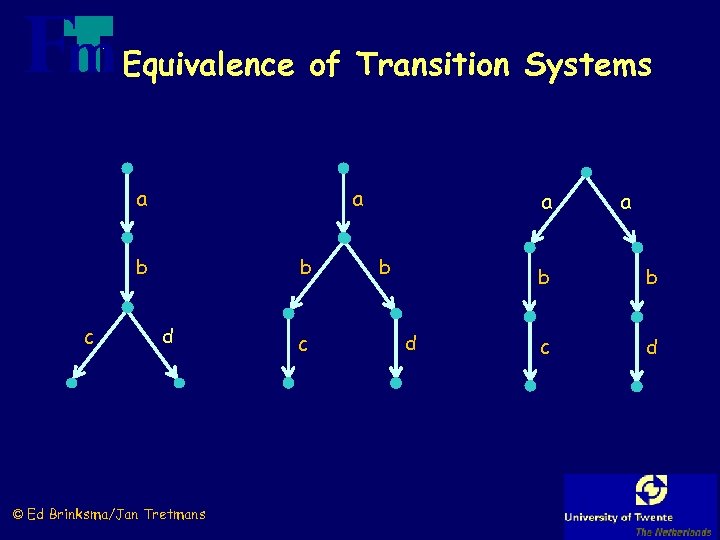
Equivalence of Transition Systems a a b b c d © Ed Brinksma/Jan Tretmans c a b d b c d
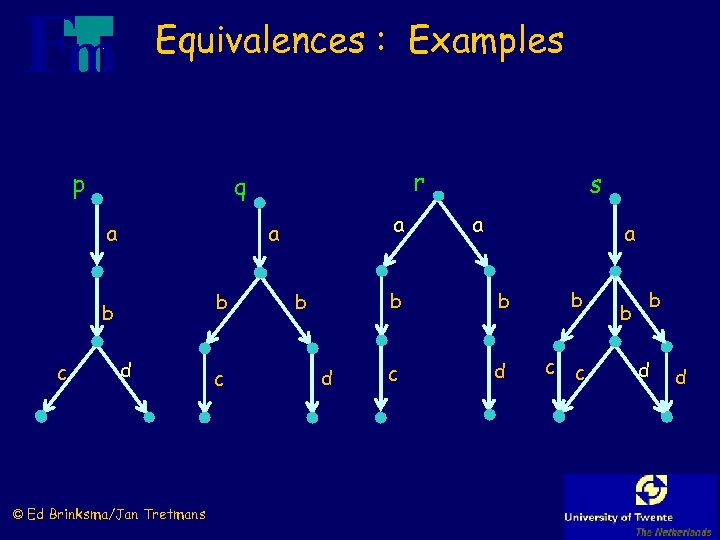
Equivalences : Examples p a a a b b c r q d © Ed Brinksma/Jan Tretmans c s a a b b d b b c d c c b b d d
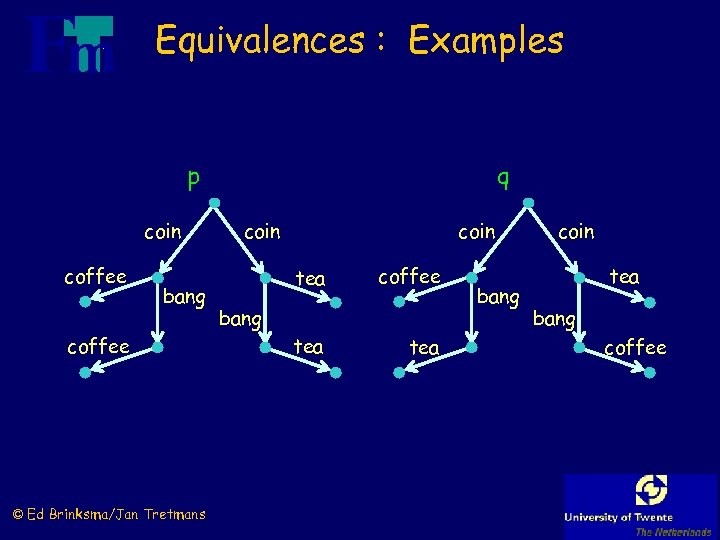
Equivalences : Examples p coin coffee bang coffee © Ed Brinksma/Jan Tretmans q coin tea bang tea coffee tea bang coin tea bang coffee
4862303c3e5a9e7b89844abfcb8a06f2.ppt