Equivalence-Based Security Specifications A Datta R Küsters J

Equivalence-Based Security Specifications A. Datta, R Küsters, J. Mitchell, A. Ramanathan, V. Shmatikov A. Scedrov, V. Teague, P. Mateus

General approach u Real protocol • The protocol we want to use • Expressed precisely in some formalism u Idealized protocol • May use unrealistic mechanisms (e. g. , private channels) • Defines the behavior we want from real protocol • Expressed precisely in same formalism u Specification • Real protocol indistinguishable from ideal protocol • Beaver ‘ 91, Goldwasser-Levin ‘ 90, Micali-Rogaway ’ 91 • Depends on some characterization of observability u Achieves compositionality

Secrecy for Challenge-Response u. Protocol P A B: { i } K B A: { f(i) } K u“Obviously’’ secret protocol Q A B: { random_number } K B A: { random_number } K

Specification with Authentication u. Protocol P A B: { random i } K B A: { f(i) } K A B: “OK” if f(i) received u“Obviously’’ authenticating protocol Q A B: { random i } K public channel private channel B A: { random j } K i , j public channel A B: “OK” private channel if private i, j match public msgs

Pseudo-random number generators u. Sequence generated from random seed Pn: let b = nk-bit sequence generated from n random bits in PUBLIC b end u. Truly random sequence Qn: let b = sequence of nk random bits in PUBLIC b end u. P is crypto strong pseudo-random number generator P Q Equivalence is asymptotic in security parameter n

Compositionality (intuition) u. Crypto primitives • Ciphertext indistinguishable from noise encryption secure in all protocols u. Protocols • Protocol indistinguishable from ideal key distribution protocol secure in all systems that rely on secure key distributions

Compositionality u. Intuitively, if: • Q securely realizes I , • R securely realizes J, • R, J use I as a component, uthen R{Q/I} securely realizes J u Fits well with process calculus because is a congruence • Q I C[Q] C[I] • contexts constructed from R, J, simulators

Three technical settings u. Canetti – Universal composability • Condition: two adversaries and environment • Computation: Communicating Turing machines u. PW, … – Black-box simulatability • Condition: one adversary, simulator, environment • Computation: I/O automata (or CT machines) u. AG, LMMRST… - Process equivalence • Condition: observational equivalence • Computation: ppoly or nondet process calculus Compare symmetric version of conditions over uniform computation model

More Background Universal Black-box Compos. Simulat. Communicating Turing Mach Canetti I/O Automata Pfitz-W Observ. Equiv. Pfitz-W Nondet. Process Calc Prob Poly Process Calc Spi, Applied LMMRST

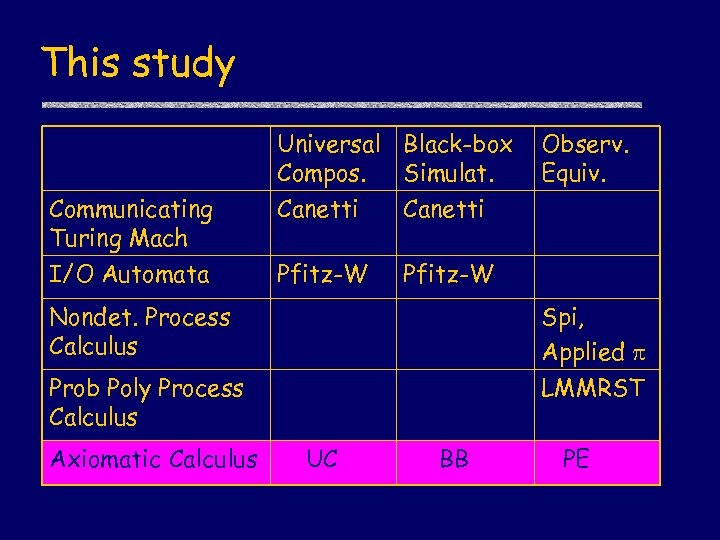
This study Universal Black-box Compos. Simulat. Communicating Turing Mach Canetti I/O Automata Pfitz-W Observ. Equiv. Pfitz-W Nondet. Process Calculus Spi, Applied LMMRST Prob Poly Process Calculus Axiomatic Calculus UC BB PE

Ideal functionality (UC, BB) u. What is the ideal key exchange protocol? • Clients ask server for key, receive response? • Server chooses keys and sends secretly? u. Issue • Easy to distinguish number of messages • No “canonical” key exchange protocol is equivalent to all secure key exchange protocols u. Ideal functionality • Not a protocol with number of messages, etc. • A functionality that can be used to create ideal protocols

Adversary vs Environment (UC, BB) u. Adversary • Interacts with protocol over network • Does not choose messages to send, contract to sign, certificate authority, … u. Environment • Represents the configuration of honest users who are trying to use the protocol • Input to general protocol • Example – Kerberos TGS, KDC, clients, servers set by environment

Universal composability (UC) u. Given • Protocol P • Ideal functionality F u. Require • For every attack A 1 on P, there exists an attack A 2 on F revealing same information in any environment E • And conversely (in symmetric form of UC)

Black-box simulatability u. Given • Protocol P • Ideal functionality F u. Require • There exists a simulator S such that for any attacker A, protocols P and S F reveal same information in any environ E

Observational Equivalence u. Given • Protocol P • Ideal protocol Q (not functionality F) u. Require • Protocols P and Q reveal same information in any context No simulator, context = attacker + env

Comparison u. UC and BB use “ideal functionality” + Allows single specification, regardless of communication pattern of protocol u. Observational equivalence + Standard relation, well-known properties + Bisimulation technique + Proof system u. Separate adversary and environment - Not clear if useful, except in exposition Add ideal functionality to specification using process equivalence

Language Approach u. Write protocol in process calculus • Accepted and long-studied approach to concurrency u. Express security using observational equivalence • Standard relation from programming language theory P Q iff for all contexts C[ ], same observations about C[P] and C[Q] • Inherently compositional • Context represents adversary u. Use proof rules for to prove security • Protocol is secure if no adversary can distinguish it from some idealized version of the protocol

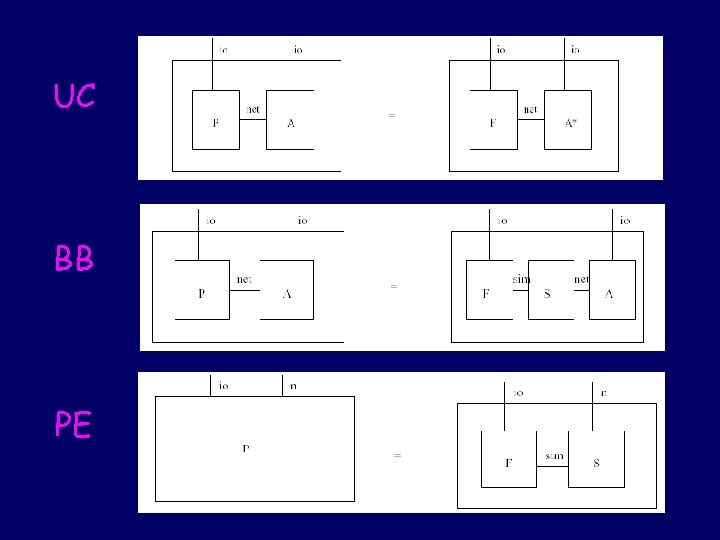
UC BB PE

Rest of talk u. Process calculus summary u. Formal definition of relations u. Sketch proof of equivalences u. Future directions

Syntax u. Bounded -calculus with integer terms P : : = 0 | cq(|n|) T | cq(|n|) (x). P | cq(|n|). P | [T=T] P | P|P | ! q(|n|). P send up to q(|n|) bits receive private channel test parallel composition bounded replication Terms may contain symbol n; channel width and replication bounded by poly in |n|

Equational principles u. P | Q Q | P u. P | (Q | R) (P | Q) | R u. P | 0 P u c. P d. [d/c]P same bandwidth, … u c. C[P] C[ c. P] c channels( C[0] ) u. P Q Q P u. P Q, Q R P R u. P Q C[P] C[Q] Prove results using these properties of process calculus; true for TM, IOA

Formal definitions u. Universal composability A 1 A 2. net(P | A 1) net(F | A 2) u. Black-box simulability S A. net(P | A) net( sim(F|S)|A) u. Process equivalence S. P sim(F | S) Notes • Relation includes quantifying over environments • Divide channels into network channels, simulator channels, environment channels

Results u. UC and BB • Equivalent w/synchronous communication • Equivalent w/asynchronous communication u. BB and Process Equivalence (PE) • PE implies BB in synch communication • PE equivalent BB with asynch communication These results are proved formally in process calculus (we worked out soundness for PPC and spi-calculus). Results hold for any computational framework satisfying equational principles given in earlier slide

Proof sketch (also have nice pictures) u PE BB UC : Easy. Congruence and quantifier order. u UC BB u BB PE

Key Lemmas u. Lemma 6. Scope Extrusion • c. (P | Q) ( c. P) | Q c channels( Q ) u. Lemma 8. Double buffering • One asynchronous buffer is indistinguishable from the composition of two u. Lemma 9. Dummy adversary and buffer • Composing a dummy adversary (that just sends network information to the environment) with asynchronous buffer is indistinguishable from a buffer alone

Synchronous communication u Buffering fails • With synchronous communication, adding a buffer or dummy adversary can change the observable order of actions

Some future directions u. Complete this study • Relate computational models • Look at asymmetric specifications – P is at least as secure as Q u. Relate logical specification methods • Equivalence P Q – P is detailed, Q more abstract • Properties of Q – Prove Q achieves authenticated key exchange