Equation-Based Modeling Copyright 2014 COMSOL COMSOL Multiphysics

Equation-Based Modeling © Copyright 2014 COMSOL, COMSOL Multiphysics, Capture the Concept, COMSOL Desktop, and Live. Link are either registered trademarks or trademarks of COMSOL AB. All other trademarks are the property of their respective owners, and COMSOL AB and its subsidiaries and products are not affiliated with, endorsed by, sponsored by, or supported by those trademark owners. For a list of such trademark owners, see www. comsol. com/trademarks

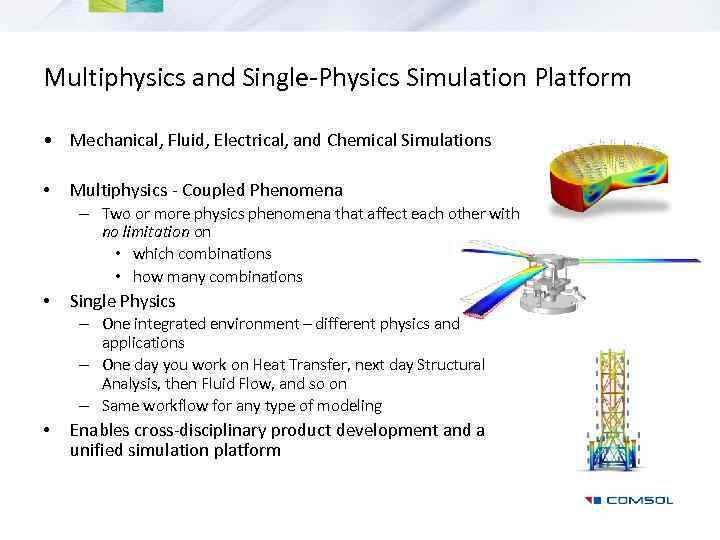
Multiphysics and Single-Physics Simulation Platform • Mechanical, Fluid, Electrical, and Chemical Simulations • Multiphysics - Coupled Phenomena – Two or more physics phenomena that affect each other with no limitation on • which combinations • how many combinations • Single Physics – One integrated environment – different physics and applications – One day you work on Heat Transfer, next day Structural Analysis, then Fluid Flow, and so on – Same workflow for any type of modeling • Enables cross-disciplinary product development and a unified simulation platform

Highly Customizable and Adaptable • Create your own multiphysics couplings • Customize material properties and boundary conditions – Type in mathematical expressions, combine with look-up tables and function calls • User-interfaces for differential and algebraic equations • Parameterize on material properties, boundary conditions, geometric dimensions, and more • High-Performance Computing (HPC) – Multicore & Multiprocessor: Included with any license type – Clusters & Cloud: With floating network licenses

Product Suite – COMSOL 4. 4

When is Equation-Based Modeling Needed? • Try to avoid equation-based modeling if possible! – Using built-in physics interfaces enables ready-made postprocessing variables and other tools for faster model setup with much lower risk of human error • Applications that previously required equation-based modeling but now has a dedicated physics interface: – Fluid-Structure Interaction (Structural Mechanics Module, MEMS Module) – Surface adsorption and reactions (Chemical Reaction Engineering Module, Plasma Module) – Shell-Acoustics and Piezo-Acoustics (Acoustics Module) – Thermoacoustics (Acoustics Module) – and many more…

When is Equation-Based Modeling Needed? • Try to avoid equation-based modeling if possible! • But: we don’t have every imaginable physics equation builtinto COMSOL (yet!). So there is sometimes a need for custom modeling.

Custom-Modeling in COMSOL • COMSOL Multiphysics® allows you to model with PDEs or ODEs directly: – Use one of the equation-template user interfaces • You do *not* need to write “user-subroutines” in COMSOL to implement your own equation! – Benefit: COMSOL’s nonlinear solver gets all the nonlinear info with gradients and all. Faster and more robust convergence.

Customization Approaches • Four modeling approaches: 1. Ready-made physics interfaces 2. First principles with the equation templates 3. Start with ready-made physics interface and additional terms. 4. Start with a ready-made physics interface and add your own separate equation (PDE, ODE) to represent physics that is not already available as a ready-made application mode • Also: – The Physics Builder lets you create your own user interfaces that hides the mathematics for your colleagues and customers

Linear Model Problems: Fundamental Phenomena • Laplace’s equation • Heat equation • Wave equation • Helmholtz equation • Convective Transport equation

COMSOL PDE Modes: Graphical User Interfaces • Coefficient form • General form • Weak form • All these can be used for scalar equations or systems • Which to use? – Whichever is more convenient for you and your simulation needs

Coefficient Form inside domain on boundary • Coefficient Matching Example: Poisson’s equation inside subdomain on subdomain boundary Implies c=f=h=1 and all other coefficients are 0.

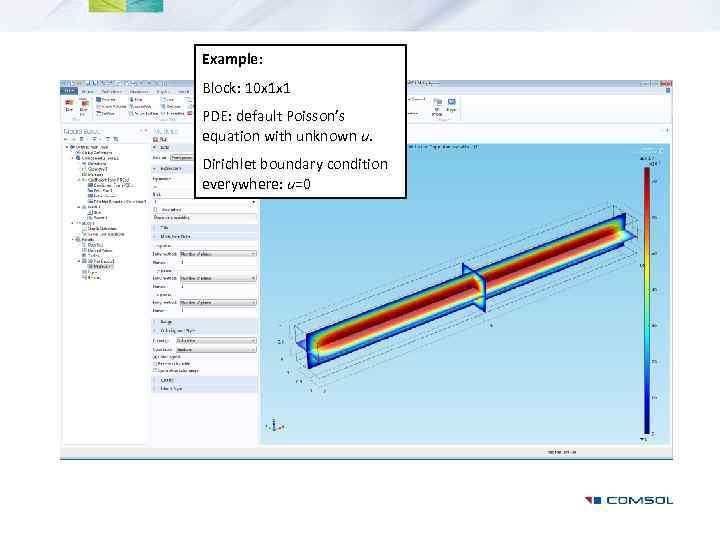
Example: Block: 10 x 1 x 1 PDE: default Poisson’s equation with unknown u. Dirichlet boundary condition everywhere: u=0

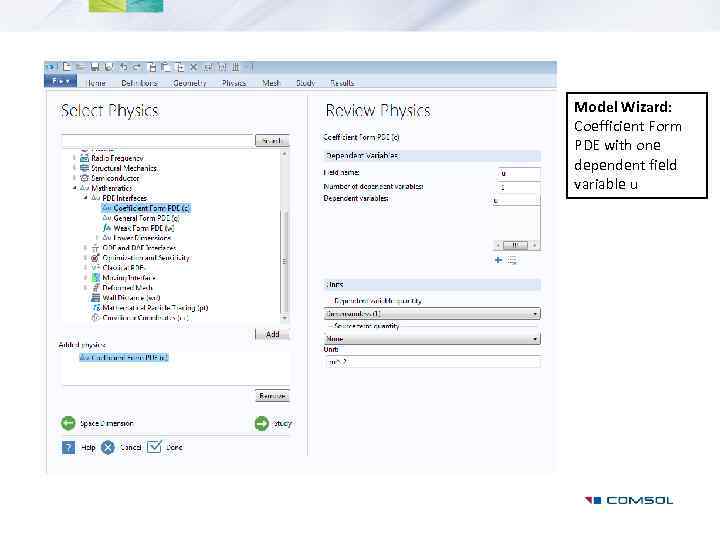
Model Wizard: Coefficient Form PDE with one dependent field variable u

Stationary study

Geometry: block 10 -by-1 -by 1. Units in meters (SI).

Coefficient Form PDE with c=1, a=0, f=1

Mass Coefficients are inactive due to Stationary Study

Dirichlet Boundary Condition

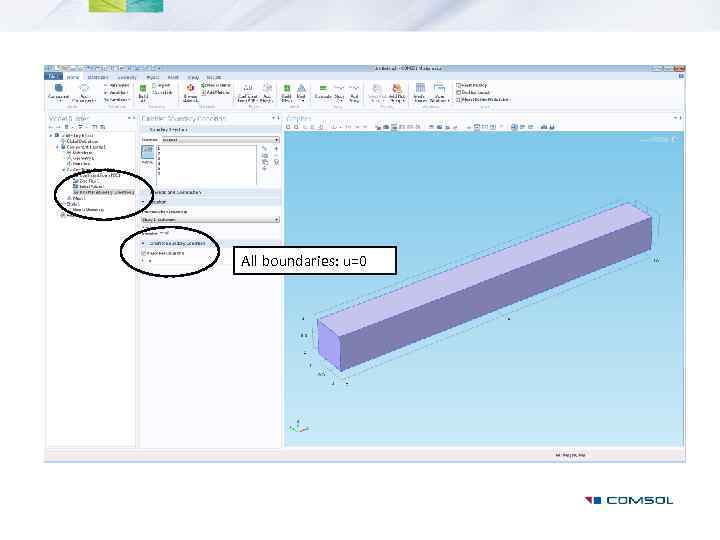
All boundaries: u=0

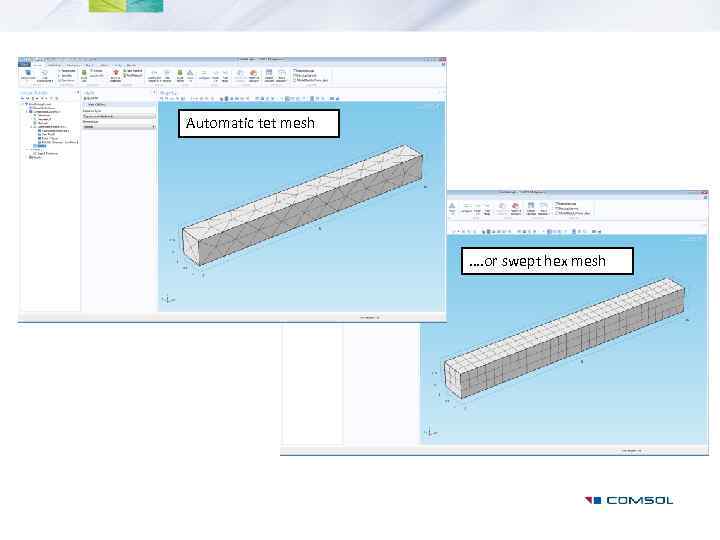
Automatic tet mesh …. or swept hex mesh

Control over shape function and element order

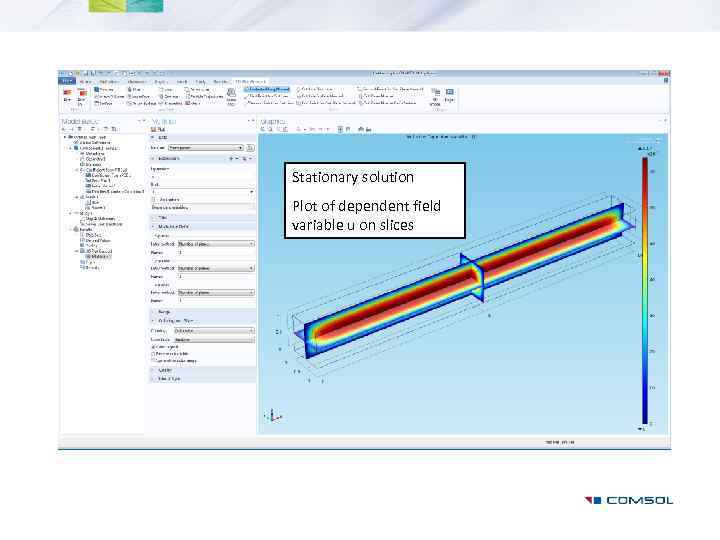
Stationary solution Plot of dependent field variable u on slices

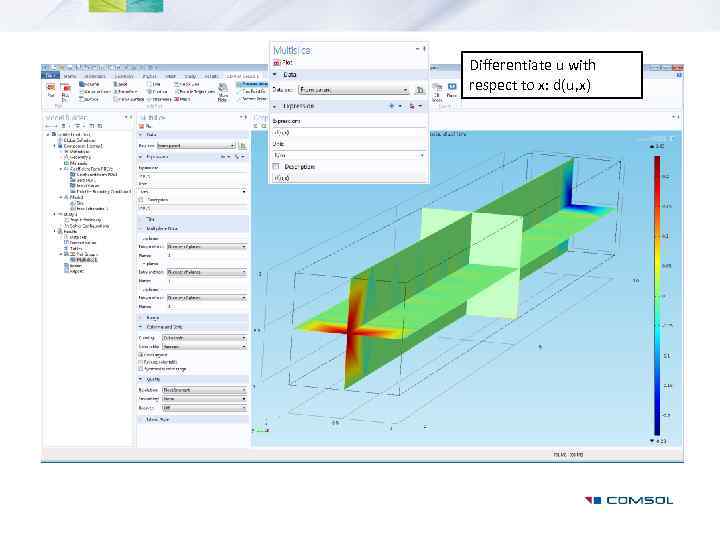
Differentiate u with respect to x: d(u, x)

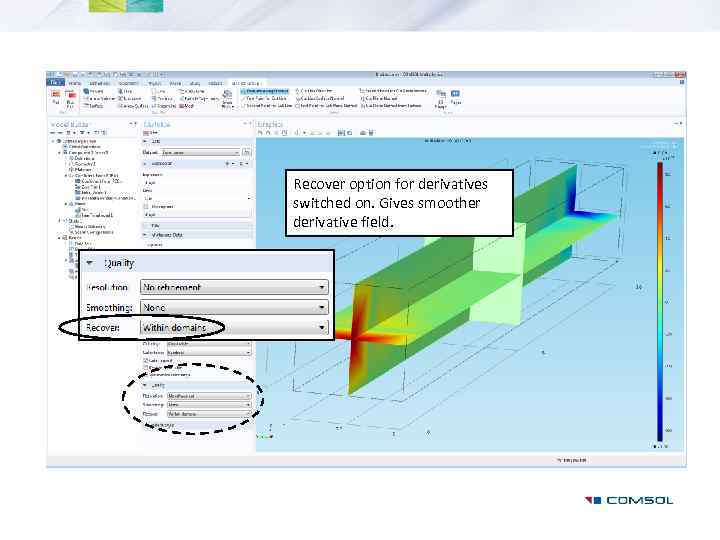
Recover option for derivatives switched on. Gives smoother derivative field.

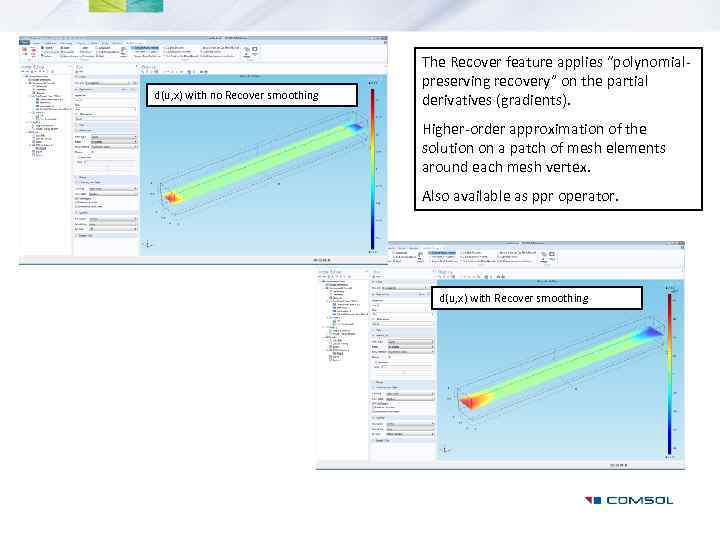
d(u, x) with no Recover smoothing The Recover feature applies “polynomialpreserving recovery” on the partial derivatives (gradients). Higher-order approximation of the solution on a patch of mesh elements around each mesh vertex. Also available as ppr operator. d(u, x) with Recover smoothing

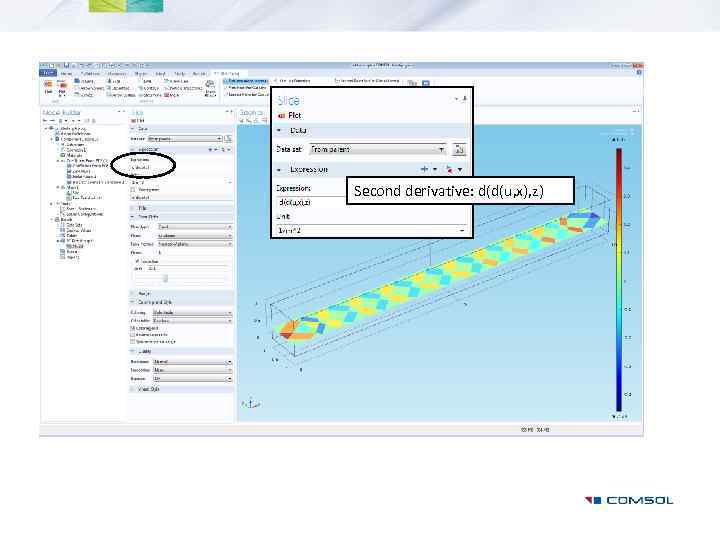
Second derivative: d(d(u, x), z)

Coefficient Form, Interpretations diffusion mass damping/ mass convection source absorption convection source

Coefficient Form, Structural Analysis Wave Equation elastic stress mass damped mass initial/thermal stress body force (gravitation) density damping coefficient stress, u= displacement vector stiffness, “spring constant”

Coefficient Form, Transport Diffusion Equation diffusion accumulation/storage convection source absorption convection source

Coefficient Form, Steady-State Equation

Coefficient Form, Frequency-Response Wave Equation diffusion Helmholtz term source Helmholtz equation: Wave number Wave length

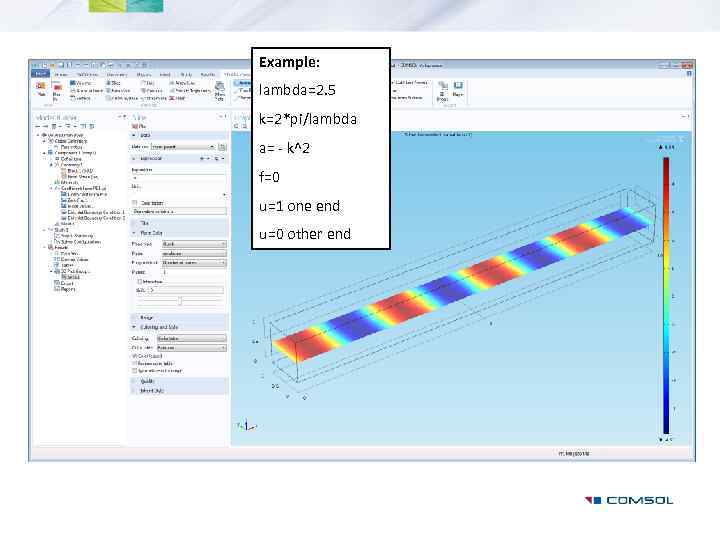
Example: lambda=2. 5 k=2*pi/lambda a= - k^2 f=0 u=1 one end u=0 other end

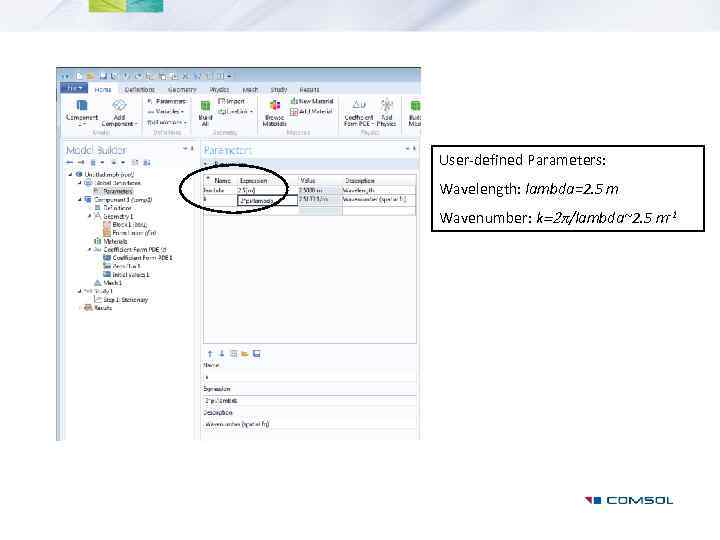
User-defined Parameters: Wavelength: lambda=2. 5 m Wavenumber: k=2 p/lambda~2. 5 m-1

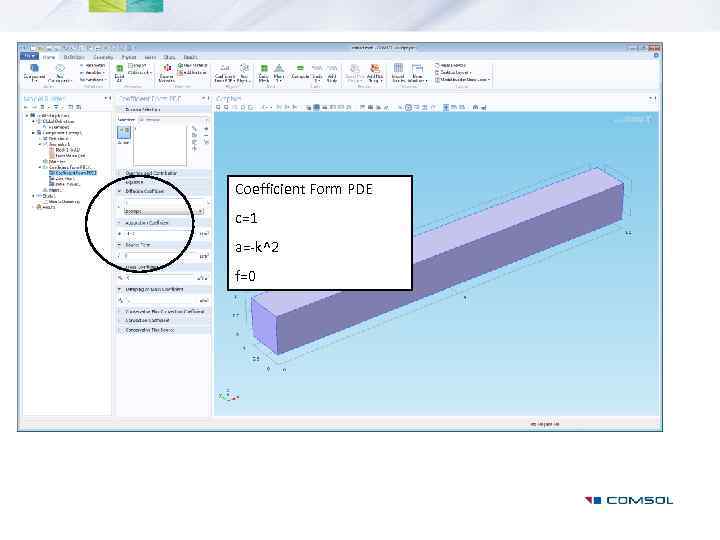
Coefficient Form PDE c=1 a=-k^2 f=0

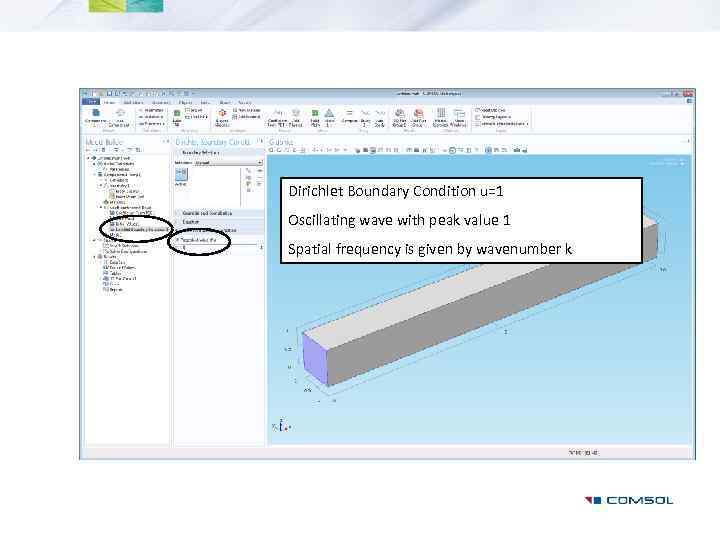
Dirichlet Boundary Condition u=1 Oscillating wave with peak value 1 Spatial frequency is given by wavenumber k

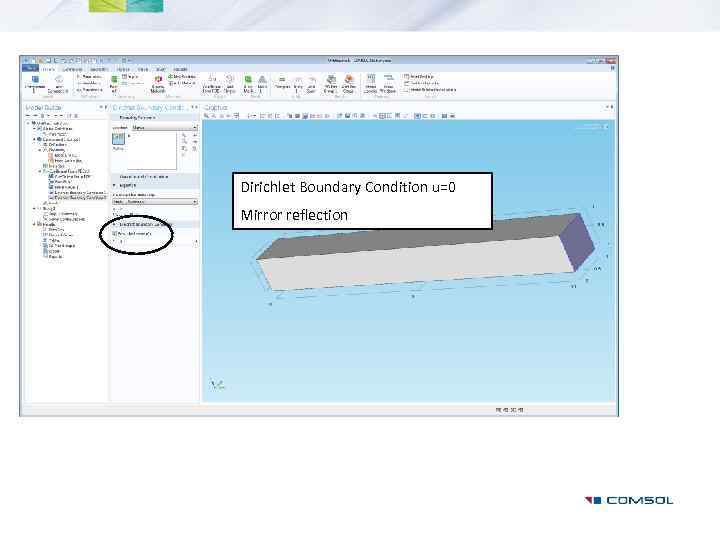
Dirichlet Boundary Condition u=0 Mirror reflection

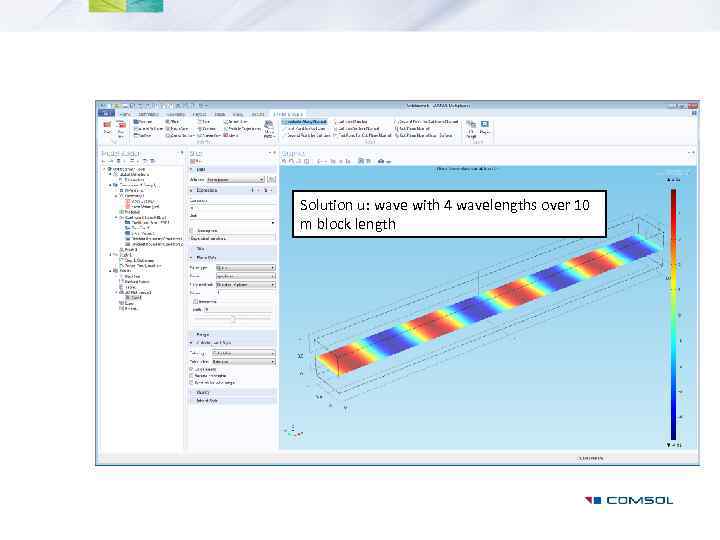
Solution u: wave with 4 wavelengths over 10 m block length

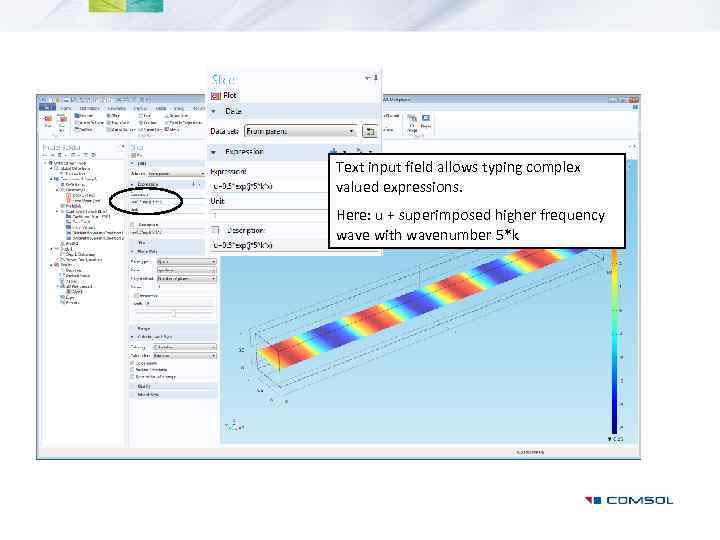
Text input field allows typing complex valued expressions. Here: u + superimposed higher frequency wave with wavenumber 5*k

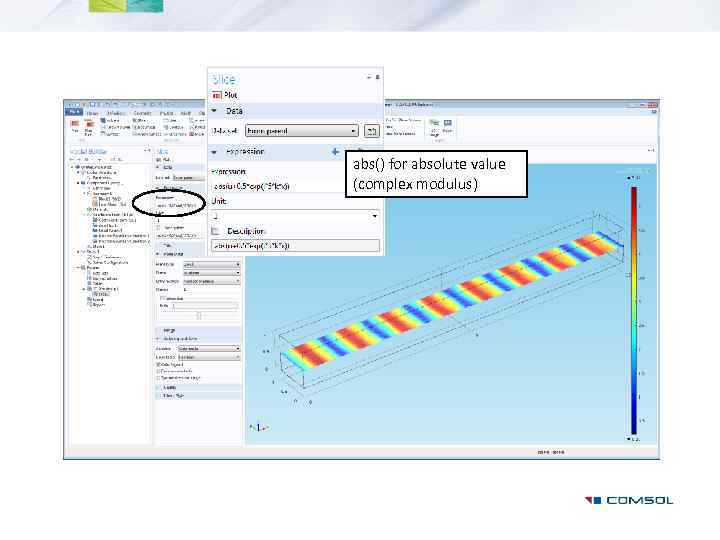
abs() for absolute value (complex modulus)

Complex Arithmetics • Can compute: real(w) imag(w) abs(w) arg(w) conj(w)

General Form – A more compact formulation • inside domain • on domain boundary • For Poisson’s equation, the corresponding general form implies • All other coefficients are 0

Weak Form • Think of the weak form as a generalization of the principal of virtual work (for those familiar with that) with virtual displacement du – The test function n ~ du • Convection-diffusion equation: • Multiply by test function n and integrate: • Integrate by parts and use boundary conditions: • In COMSOL you can type the integrands of this integral expression: Weak Form PDE

Typing the Weak Form c*grad(u) ·grad(test(u))= c*grad(u) ·test(grad(u))= c*(ux*test(ux)+uy*test(uy)+uz*test(uz)) Note: COMSOL convention has the integral in the right-hand side so additional negative sign needed in the GUI

Modifying Variables and Equations • Enable Equation View on the Model Builder Show menu – Once enabled, Equation View stays enabled for new models • Variables, weak expressions and constraints can be modified – Modified rows are marked with warning signs • Use reset buttons to cancel modifications

Transient Diffusion Equation ~ Heat Equation diffusion accumulation/storage source

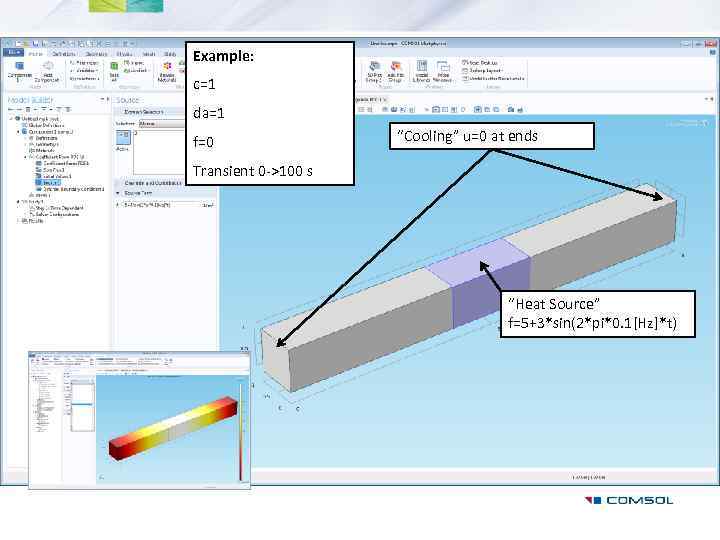
Example: c=1 da=1 f=0 “Cooling” u=0 at ends Transient 0 ->100 s “Heat Source” f=5+3*sin(2*pi*0. 1[Hz]*t)

Time Dependent study

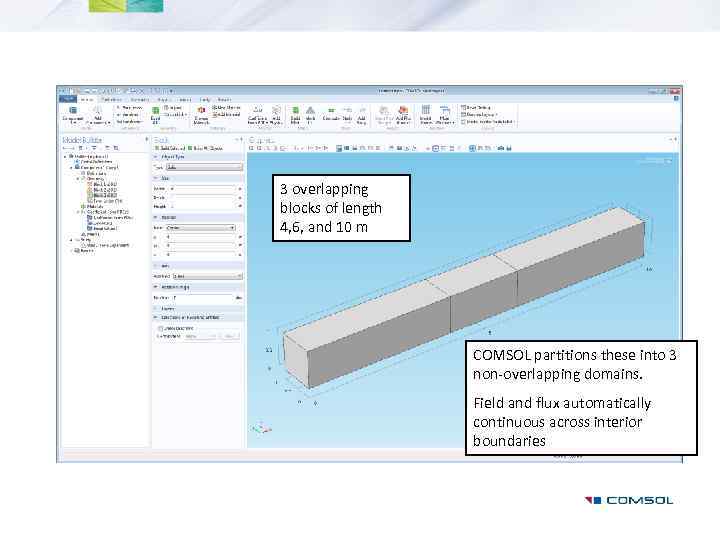
3 overlapping blocks of length 4, 6, and 10 m COMSOL partitions these into 3 non-overlapping domains. Field and flux automatically continuous across interior boundaries

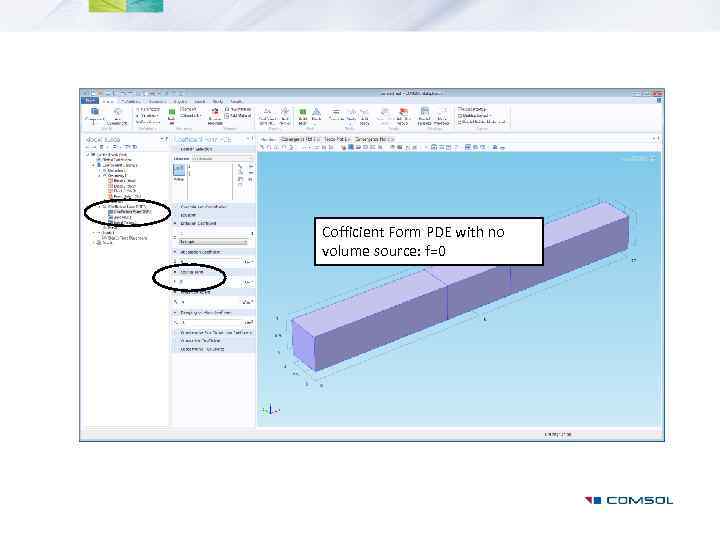
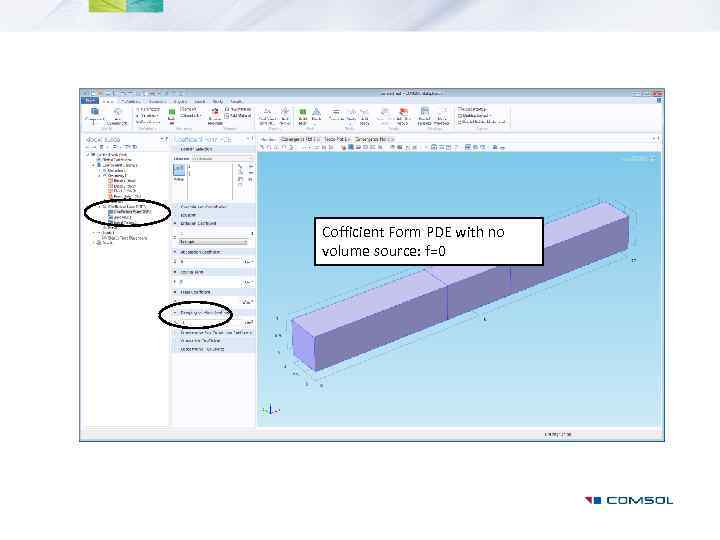
Cofficient Form PDE with no volume source: f=0

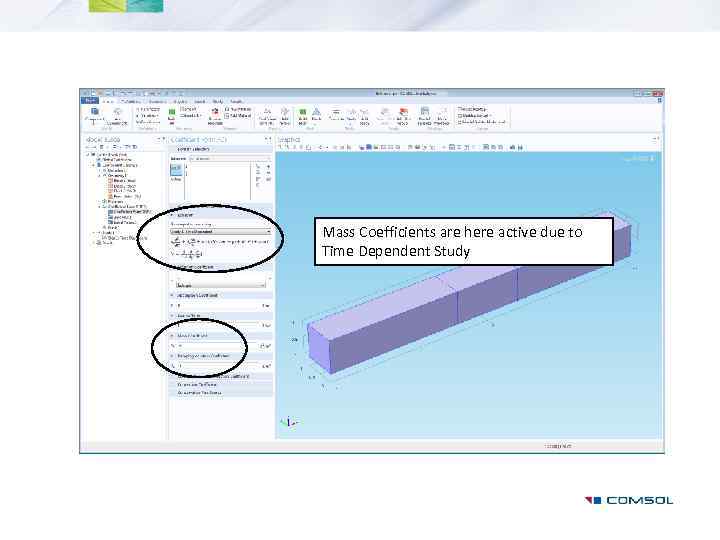
Mass Coefficients are here active due to Time Dependent Study

Superimposed source term: f=5+3*sin(2*pi*0. 1[Hz]*t)

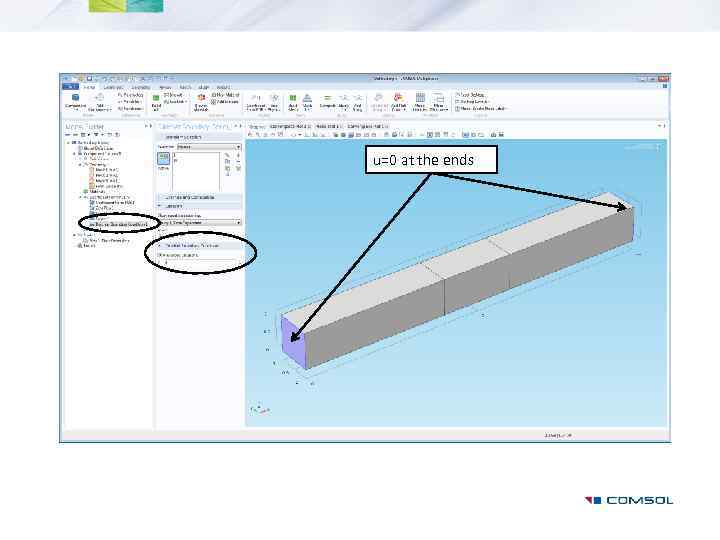
u=0 at the ends

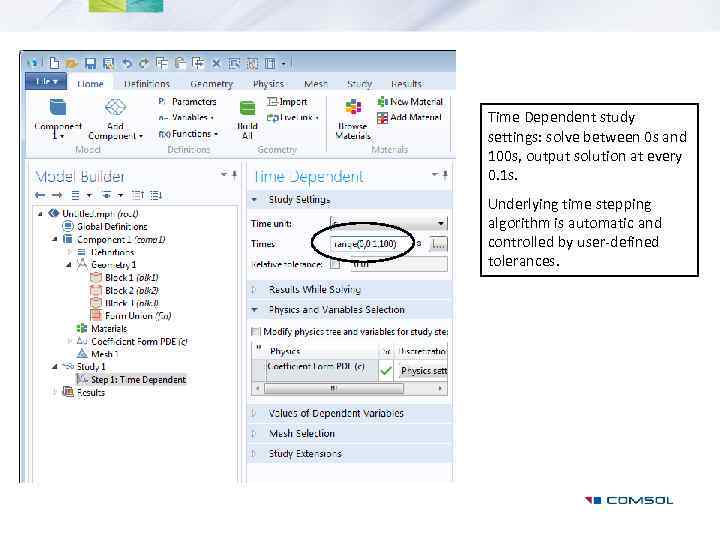
Time Dependent study settings: solve between 0 s and 100 s, output solution at every 0. 1 s. Underlying time stepping algorithm is automatic and controlled by user-defined tolerances.

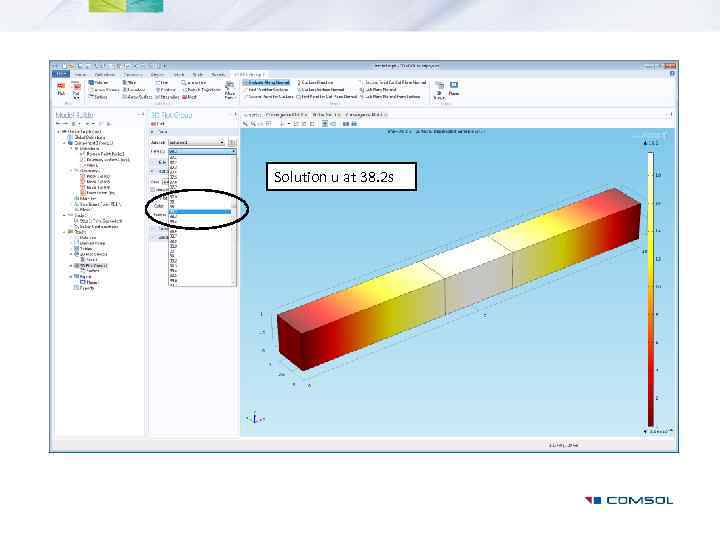
Solution u at 38. 2 s

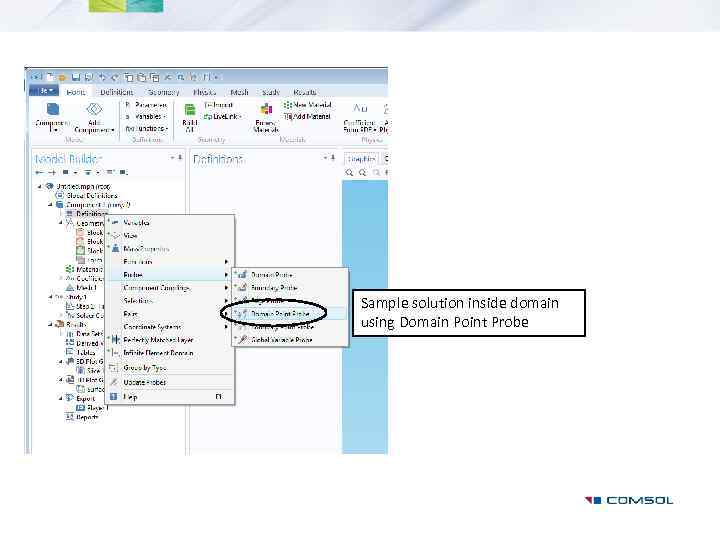
Sample solution inside domain using Domain Point Probe

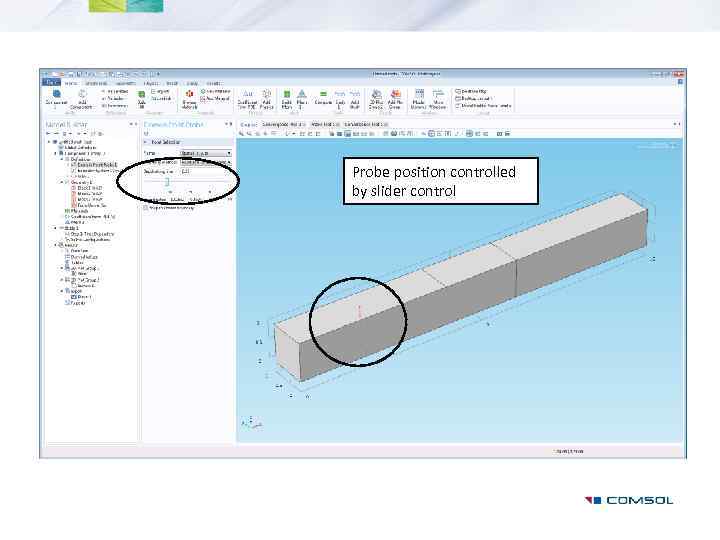
Probe position controlled by slider control

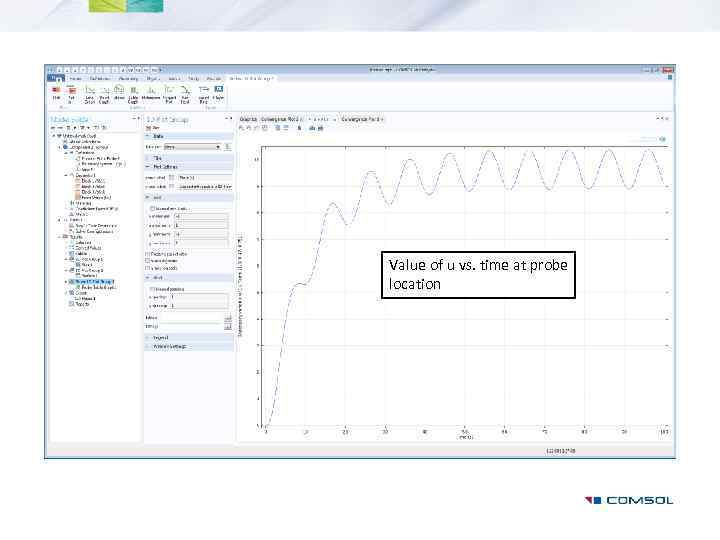
Value of u vs. time at probe location

Equation Systems • COMSOL can handle systems of equations in all of – Coefficient Form – General Form – Weak Form or combinations of the above • Easy setup from Model Wizard

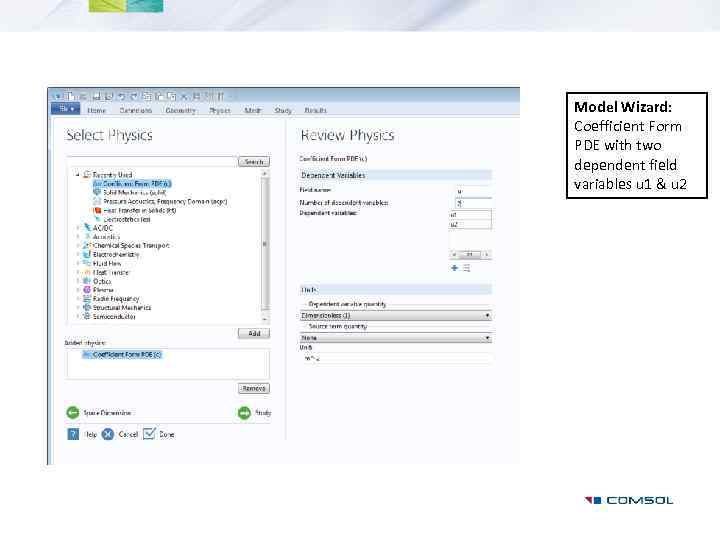
Model Wizard: Coefficient Form PDE with two dependent field variables u 1 & u 2

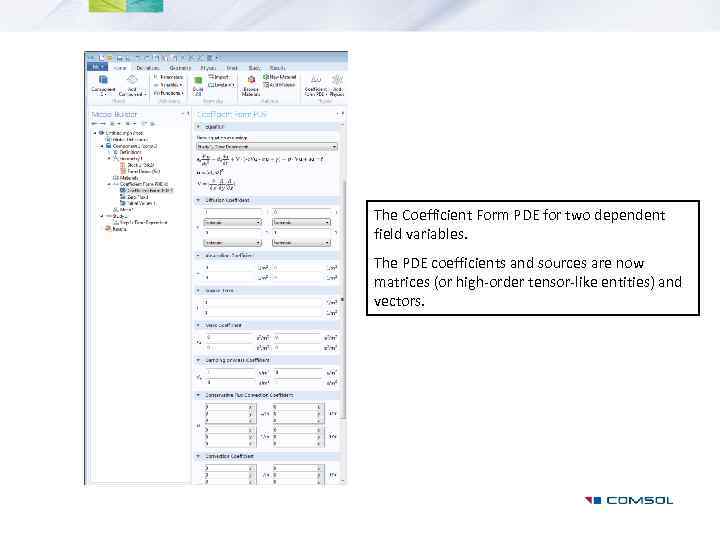
The Coefficient Form PDE for two dependent field variables. The PDE coefficients and sources are now matrices (or high-order tensor-like entities) and vectors.

Coefficient Form PDE for 2 variables in 2 D Space da c b The default coefficients corresponds to two decoupled Poisson’s equations. Fill out with nonlinear or offdiagonal coefficients, as well as nonlinear source terms for couplings. a f

Examples: Electrical Signals in a Heart, General Form PDE • Fitzhugh-Nagumo Equations • Landau-Ginzburg Equations

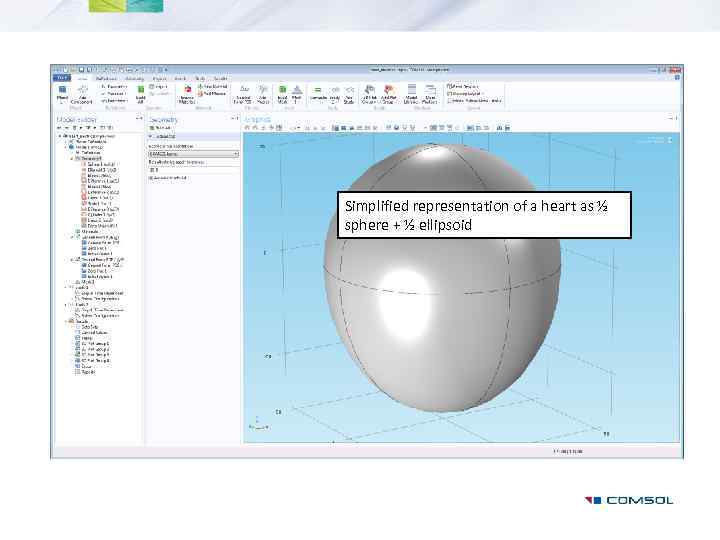
Simplified representation of a heart as ½ sphere + ½ ellipsoid

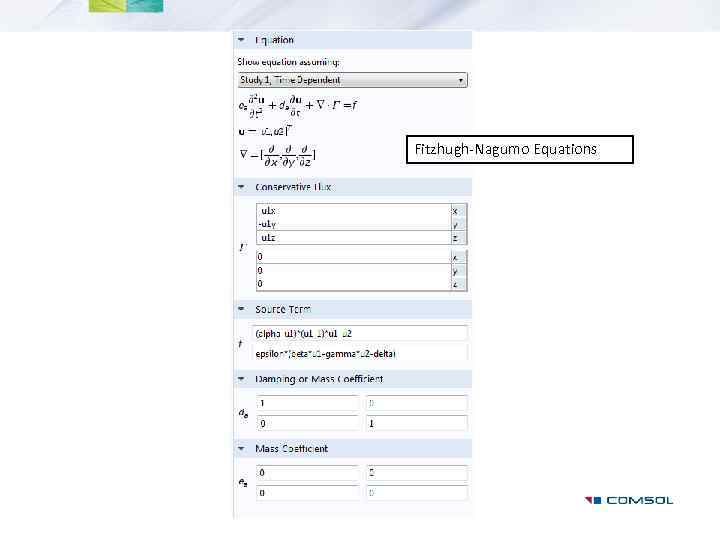
Fitzhugh-Nagumo Equations

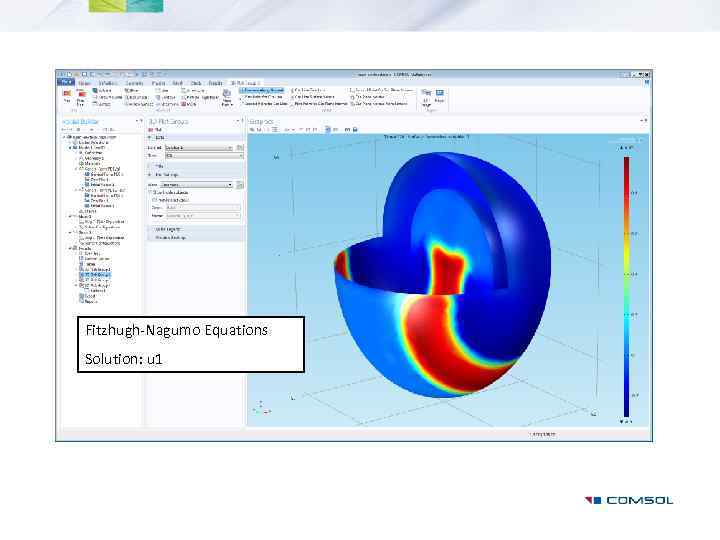
Fitzhugh-Nagumo Equations Solution: u 1

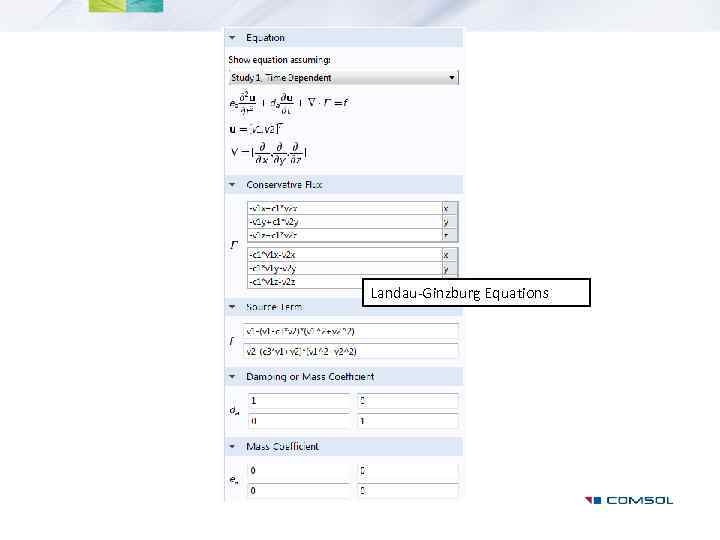
Landau-Ginzburg Equations

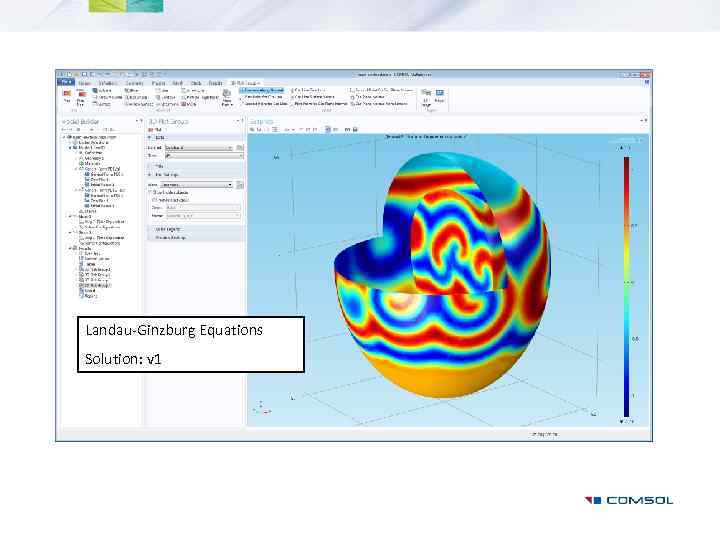
Landau-Ginzburg Equations Solution: v 1

End of Presentation