EQT 272 PROBABILITY AND STATISTICS FARAH ADIBAH ADNAN

EQT 272 PROBABILITY AND STATISTICS FARAH ADIBAH ADNAN INSTITUT E OF ENGINEERING MATHEMATICS (IMK) UNIVERSITI MALAYSIA PERLIS Free Powerpoint Templates Page 1

CHAPTER 1 PROBABILITY 1. 1 Introduction 1. 2 Sample space and algebra of sets 1. 3 Properties of 1. 4 probability Tree diagrams and counting techniques 1. 5 Conditional probability 1. 6 Bayes’s theorem Free Powerpoint Templates 1. 7 Independence Page 2

What is probability? ? ? Is the measure of how likely something will occur. In general: • Probability is a measure of the likelihood of an event A occurring in any one experiment or trial. • Denoted by P (A). • Probability of all outcomes sums to 1. • The probability value is between 0 and 1. Free Powerpoint Templates Page 3

EXAMPLE

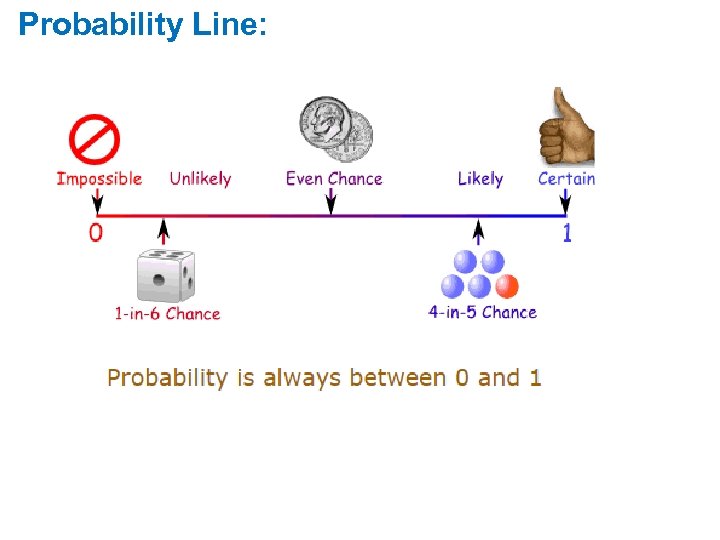
Probability Line:

The mathematical basis of probability is theory of sets. • Sets A set is a collection of things/elements. Free Powerpoint Templates Page 6

• Sample Spaces, S A sample space consists of all the possible outcomes of an experiment. • Events An event is a collection of one or more outcomes and a subset of the sample space. • Experiment An action where the result is uncertain. Eg: Toss a die, record a person’s blood type Free Powerpoint Templates Page 7

EXAMPLE

EXAMPLE • Experiment: Tossing a die • Sample space: S ={1, 2, 3, 4, 5, 6} • Events: A: Observe an odd number A={2, 4, 6} B: Observe a number less than 4 B={1, 2, 3}

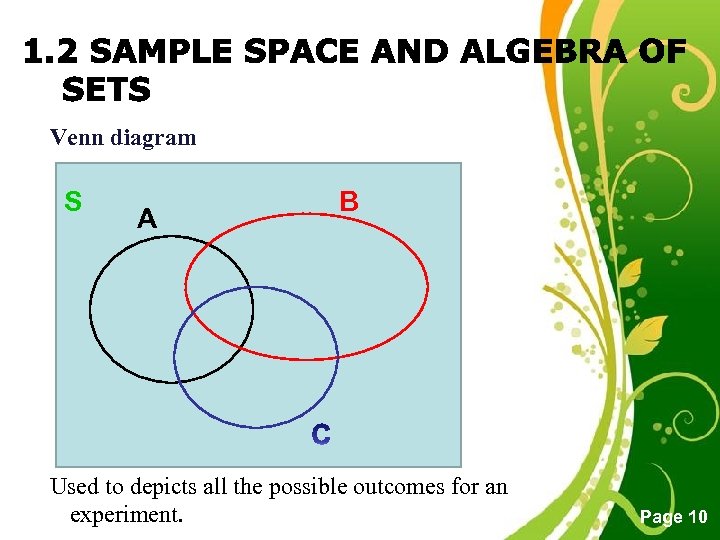
Venn diagram S A B Used to depicts all the possible outcomes for an Free Powerpoint Templates experiment. Page 10

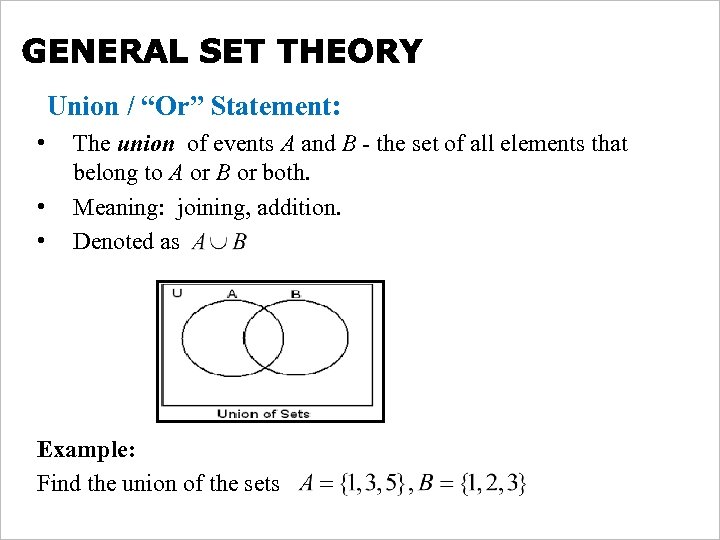
Union / “Or” Statement: • • • The union of events A and B - the set of all elements that belong to A or B or both. Meaning: joining, addition. Denoted as Example: Find the union of the sets Free Powerpoint Templates Page 11

Intersection / “And” Statement: • The intersection of events A and B - the set of all elements that belong to both A and B • Meaning: overlap, things in common. • Denoted by . Example: Find the intersection of the sets Free Powerpoint Templates Page 12

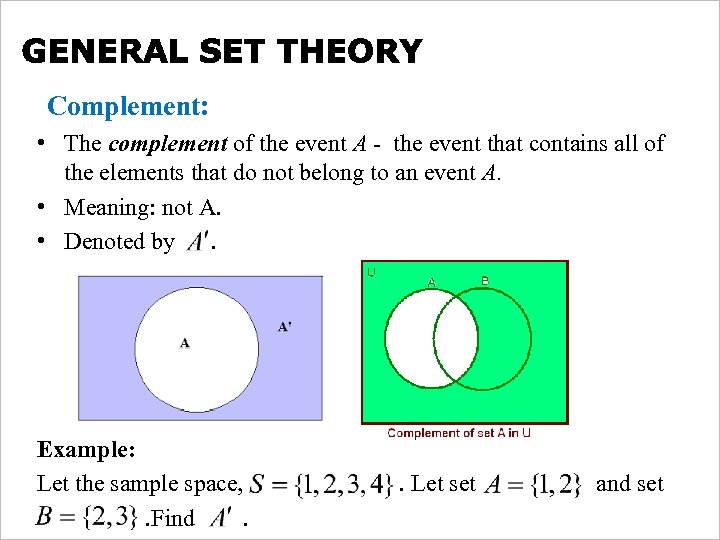
Complement: • The complement of the event A - the event that contains all of the elements that do not belong to an event A. • Meaning: not A. • Denoted by . Example: Let the sample space, . Let set and set Free Powerpoint Templates Page 13 . Find .

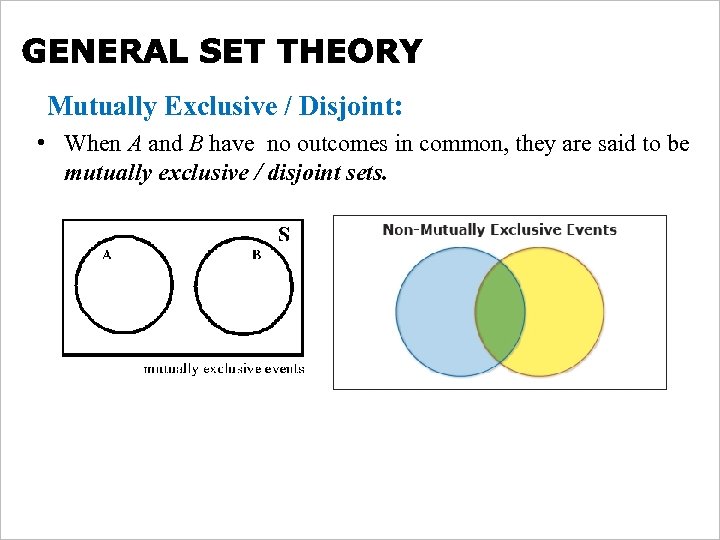
Mutually Exclusive / Disjoint: • When A and B have no outcomes in common, they are said to be mutually exclusive / disjoint sets. Free Powerpoint Templates Page 14

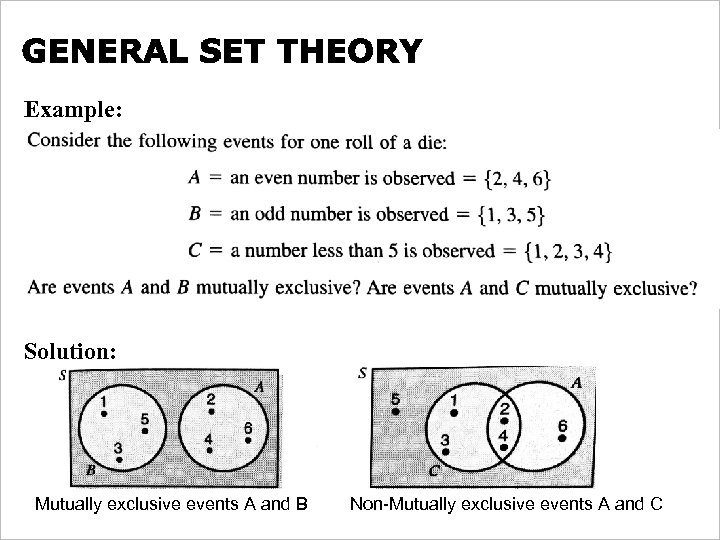
Example: Solution: Mutually exclusive events A and B Non-Mutually exclusive events A and C Free Powerpoint Templates Page 15

Exercise • Given the following sets; A= {2, 4, 6, 8, 10} B= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} C= {1, 3, 5, 11, …. }, the set of odd numbers Find , and

Answer • = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} • = {2, 4, 6, 8, …}, the set of even numbers

Exercise • A survey finds that 56% of people are married. They ask the same group of people, and 67% have at least one child. There are 41% that are married and have at least one child. Describe this results with a Venn diagram.

Exercise A group of 100 factory workers were questioned by a popular health magazine and 48% were found to take regular exercise. When asked about their eating habits, 67% replied that they always have breakfast. Not only that, 32% always have breakfast and exercise regularly. Describe this results with a Venn diagram.

Free Powerpoint Templates Page 20

EXAMPLE Two fair dice are thrown. Determine a) the sample space of the experiment b) the elements of event A if the outcomes of both dice thrown are showing the same digit. c) the elements of event B if the first thrown giving a greater digit than the second thrown. d) probability of event A, P(A) and event B, P(B) Free Powerpoint Templates Page 21

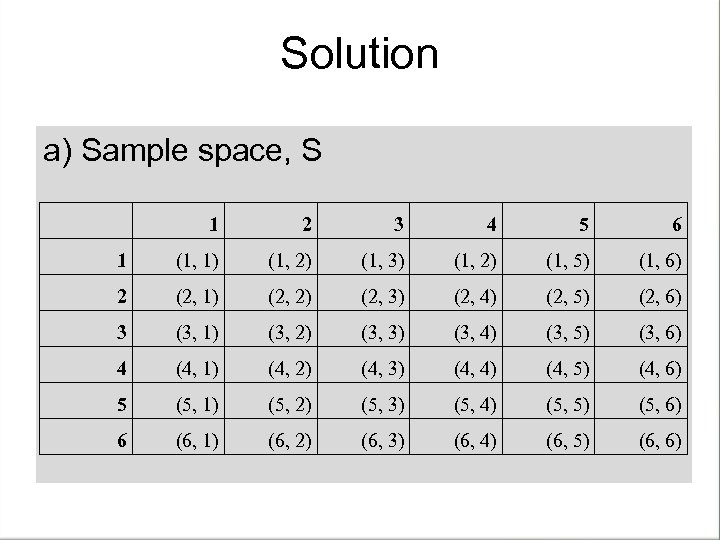
Solution a) Sample space, S 1 2 3 4 5 6 1 (1, 1) (1, 2) (1, 3) (1, 2) (1, 5) (1, 6) 2 (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) 3 (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) 4 (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) 5 (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) 6 (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) Free Powerpoint Templates Page 22

Solution b) A = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)} c) B = {(2, 1), (3, 2), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)} Free Powerpoint Templates Page 23

EXAMPLE Consider randomly selecting a Uni. MAP Master Degree international student. Let A denote the event that the selected individual has a Visa Card and B has a Master Card. Suppose that P(A) = 0. 5 and P(B) = 0. 4 and = 0. 25. a) Compute the probability that the selected individual has at least one of the two types of cards ? b) What is the probability that the selected individual has neither type of card? Free Powerpoint Templates Page 24

Solution Free Powerpoint Templates Page 25

1. 4. 1 Tree diagrams • Tree diagrams help us to u/stand probability concepts by presenting them visually. • In a tree diagram, each outcome is represented by a branch of the tree. • A tree diagram helps to find simple events. Free Powerpoint Templates Page 26

EXAMPLE A box contains one yellow and two red balls. Two balls are randomly selected and their colors recorded. Construct a tree diagram for this experiment and state the simple events. Y 1 R 2 Free Powerpoint Templates Page 27

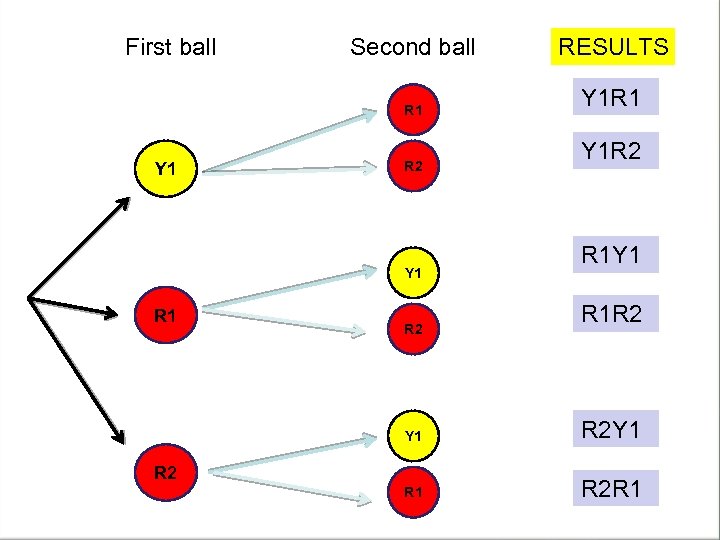
First ball Second ball R 1 Y 1 R 2 RESULTS Y 1 R 1 Y 1 R 2 R 1 Y 1 R 1 R 2 Y 1 R 2 Y 1 R 2 R 1 R 2 Free Powerpoint Templates Page 28

Exercise A couple has three children. Draw the three diagram for the possible gender of the three children. Find the probability of getting: a) Three boys b) One girl and 2 boys Free Powerpoint Templates Page 29

1. 4. 2 Counting technique • We can use counting techniques or counting rules to # find the number of ways to accomplish the experiment # find the number of simple events. # find the number of outcomes Free Powerpoint Templates Page 30

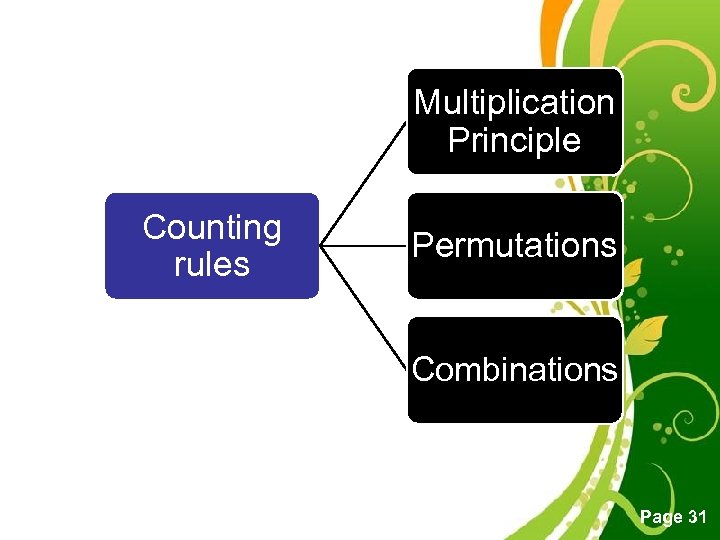
Multiplication Principle Counting rules Permutations Combinations Free Powerpoint Templates Page 31

Multiplication Principle • Is used to find the total number of outcomes. • If an experiment consists of 3 steps, and if the first step can result in m outcomes, then the second step in n outcomes, and the third step in k outcomes, the formula is: Total Outcomes =

Multiplication Principle Example: • Suppose we toss a coin 3 times. Determine the total outcomes for tosses of a coin. • This experiment has 3 steps: the first toss, the second toss, and the third toss. Each step has 2 outcomes, head and tail. Thus, total outcomes = 2 x 2 = 8. The 8 outcomes for this experiment are HHH, HHT, HTH, HTT, THH, THT, TTH, TTT

Permutations • All possible arrangements of a collection of things, where the order is important. • There are basically two types of permutation: a) Repetition is Allowed: such as a lock. It could be "333". b) No Repetition: for example the first three people in a running race. You can't be both first and second.

a) Repetition is Allowed • When you have n things to choose from . . . you have n choices each time! • When choosing r of them, the permutations are: • n ×. . . (r times) • (In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time. ) • Which is easier to write down using an exponent of r: n. Free Powerpoint Templates = nr × n ×. . . (r times) Page 35

• Example: • In a lock , there are 10 numbers to choose from (0, 1, . . 9) and you choose 3 of them: • 10 ×. . . (3 times) = 103 = 1, 000 permutations Free Powerpoint Templates Page 36

b) No Repetition • In this case, you have to reduce the number of available choices each time. • For example, what order could 16 pool balls be in? • After choosing a ball, you can't choose it again. Free Powerpoint Templates Page 37

• So, your first choice would have 16 possibilites, and your next choice would then have 15 possibilities, then 14, 13, etc. And the total permutations would be: 16 × 15 × 14 × 13 ×. . . = 20, 922, 789, 888, 000 • But maybe you don't want to choose them all, just 3 of them, so that would be only: 16 × 15 × 14 = 3, 360 • In other words, there are 3, 360 different ways that 3 pool balls could be selected out of 16 balls. Free Powerpoint Templates Page 38

Permutations • The number of ways to arrange an entire set of n distinct items is Free Powerpoint Templates Page 39

Permutations • This counting rule count the number of outcomes when the experiment involves selecting r objects from a set of n objects when the order of selection is important. Free Powerpoint Templates Page 40

• "The password of the safe was 472". • We do care about the order. "724" would not work, nor would "247". It has to be exactly 4 -7 -2. • To help you to remember, think "Permutation. . . Position" Free Powerpoint Templates Page 41

EXAMPLE • Suppose you have 3 books, A, B and C but you have room for only two on your bookshelf. In how many ways can you select and arrange the two books when the order is important. A B C

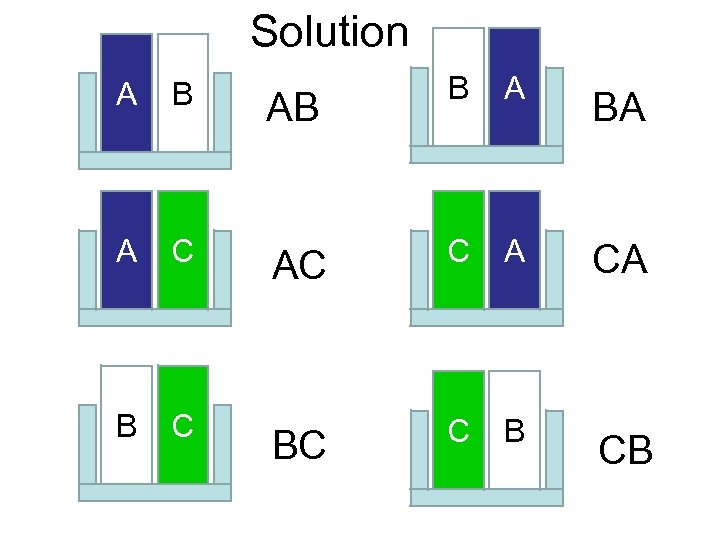
Solution A B A C A B C AB B A BA AC C A CA BC A C C B CB

There are 6 ways to select and arrange the books in order. Free Powerpoint Templates Page 44

Exercise Three lottery tickets are drawn from a total of 50. If the tickets will be distributed to each of the employees in the order in which they are drawn, the order will be important. How many simple events are associated with the experiment? Free Powerpoint Templates Page 45

Combinations • A collection of things, in which the order does not matter. Example: You are making a sandwich. How many different combinations of 2 ingredients can you make with cheese, mayo and ham? Answer: {cheese, mayo}, {cheese, ham} or {mayo, ham} Free Powerpoint Templates Page 46

Combinations • Formula: • It is often called "n choose r" Free Powerpoint Templates Page 47

EXAMPLE • Suppose you have 3 books, A, B and C but you have room for only two on your bookshelf. In how many ways can you select and arrange the two books when the order is not important. A B C Free Powerpoint Templates Page 48

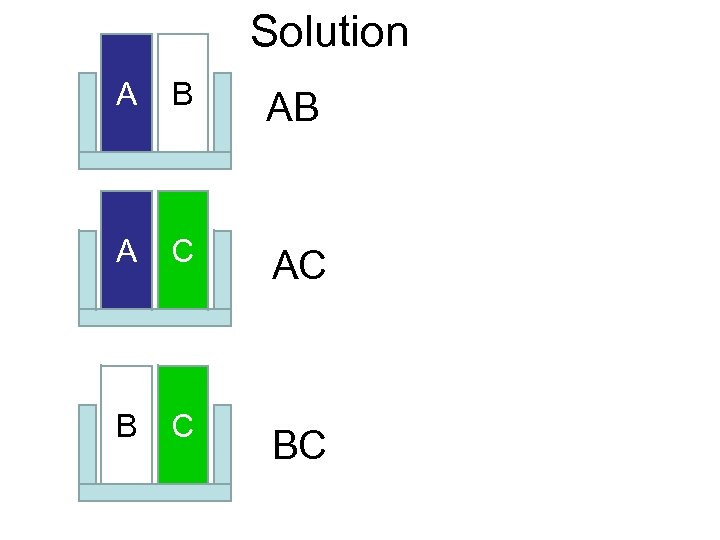
Solution A B AB A C AC A B C BC

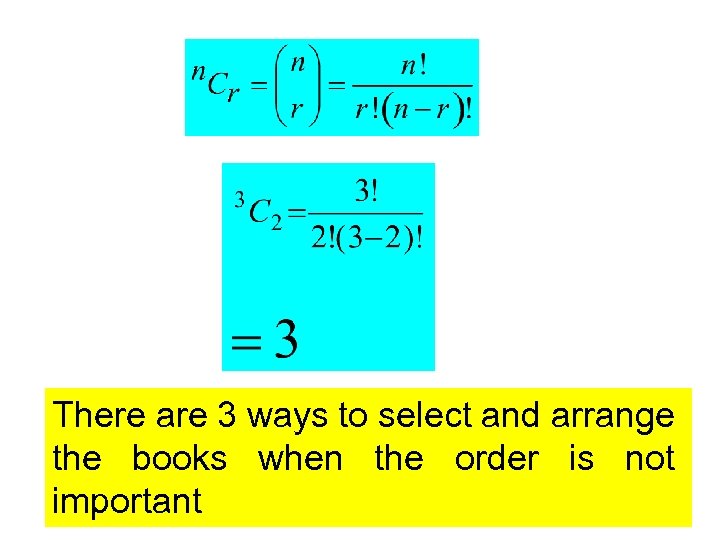
There are 3 ways to select and arrange the books when the order is not important

Exercise Suppose that in the taste test, each participant samples 8 products and is asked the 3 best products, but not in any particular order. Calculate the number of possible answer test. Free Powerpoint Templates Page 51

• Definition: q For any two events A and B with P(B) > 0, the conditional probability of A given that B has occurred is defined by GIVENFree Powerpoint Templates Page 52

EXAMPLE A study of 90 students was done by Uni. MAP first year students. The results are given in the table : Area/Gender Male (C) Female (D) Total Urban (A) 35 10 45 Rural (B) 25 20 45 Total 60 30 90 If a student is selected at random and have been told that the individual is a male student, what is the probability of he is from urban area? Free Powerpoint Templates Page 53

Solution Probability of male students from urban area Free Powerpoint Templates Page 54

EXAMPLE In 2006, Edaran Automobil Negara (EON) will produce a multipurpose national car (MPV) equipped with either manual or automatic transmission and the car is available in one of four metallic colours. Relevant probabilities for various combinations of transmission type and colour are given in the accompanying table: Transmission type/Colour Automatic, (A) Manual Grey (C) Blue Black (B) Red 0. 15 0. 10 0. 15 0. 05 0. 15 0. 20 Free Powerpoint Templates Page 55

EXAMPLE • Let, A = automatic transmission B = black C = grey Calculate; Free Powerpoint Templates Page 56

Solution a) P(A) = probability of MPV with automatic transmission P(A) = 0. 15+0. 10+0. 10 = 0. 45 P(B) = probability of black MPV P(B) = 0. 10+0. 15 = 0. 25 P(A∩B) = probability of black MPV with automatic transmission P(A∩B) = 0. 10 Free Powerpoint Templates Page 57

P(A|B) = probability of auto MPV given that the MPV is black P(B|A) = probability of black MPV given that the MPV has automatic transmission Free Powerpoint Templates Page 58

P(A|C) = probability of auto MPV given that the MPV is grey P(A|C’) = probability of auto MPV given that the MPV is not grey Free Powerpoint Templates Page 59

-Used to revise previously calculated probabilities based on new information. -Extension of conditional probability Free Powerpoint Templates Page 60

• Suppose someone told you they had a nice conversation with someone on the train. Not knowing anything else about this conversation, the probability that they were speaking to a woman is 50%. • Now suppose they also told you that this person had long hair. It is now more likely they were speaking to a woman, since women are more likely to have long hair than men. • Bayes' theorem can be used to calculate the probability that the person is a woman. Free Powerpoint Templates Page 61

• Suppose it is also known that 75% of women have long hair. Likewise, suppose it is known that 15% of men have long hair. • Our goal is to calculate the probability that the conversation was held with a woman, given the fact that the person had long hair. Free Powerpoint Templates Page 62

• Probability that the conversation was held with a woman, given the fact that the person had long hair Free Powerpoint Templates Page 63

Free Powerpoint Templates Page 64

EXAMPLE A drilling company has estimated a 40% chance of striking oil for their new well. A detailed test has been scheduled for more information. Historically, 60% of successful wells have had detailed tests, and 20% of unsuccessful wells have detailed tests. Given that this well has been scheduled for a detailed test, what is the probability that the well will be successful? Free Powerpoint Templates Page 65

Solution Free Powerpoint Templates Page 66

TRY!!! • You have a database of 100 emails. • 60 of those 100 emails are spam – 48 of those 60 emails that are spam have the word "buy" – 12 of those 60 emails that are spam don't have the word "buy" • 40 of those 100 emails aren't spam – 4 of those 40 emails that aren't spam have the word "buy" – 36 of those 40 emails that aren't spam don't have the word "buy" • What is the probability that an email is spam if it has the word "buy"? Free Powerpoint Templates Page 67

• Definition : q Two events A and B are said to be independent if and only if either Otherwise, the events are said to be dependent. Free Powerpoint Templates Page 68

• Two events, A and B, are independent if the fact that A occurs does not affect the probability of B occurring. Free Powerpoint Templates Page 69

• Some other examples of independent events are: q Landing on heads after tossing a coin AND rolling a 5 on a single 6 -sided die. q Choosing a marble from a jar AND landing on heads after tossing a coin. q Choosing a 3 from a deck of cards, replacing it, AND then choosing an ace as the second card. q Rolling a 4 on a single 6 -sided die, AND then rolling a 1 on a second roll of the die. Free Powerpoint Templates Page 70

Multiplicative Rule of Probability: Free Powerpoint Templates Page 71

EXAMPLE Free Powerpoint Templates Page 72