Эпюр прямой
ПРЯМАЯ ЛИНИЯ • Прямая линия - алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением 1 - ой степени (линейное уравнение). • Общее уравнение прямой (полное): Ах+Ву+С=0, • где А, В и С - любые постоянные, причем А и В одновременно не равны нулю. Если один из коэффициентов равен нулю, уравнение называется неполным.
• • • СПОСОБЫ ГРАФИЧЕСКОГО ЗАДАНИЯ ПРЯМОЙ ЛИНИИ Для определения положения прямой в пространстве существуют следующие методы: 1. Двумя точками (А и В). Рассмотрим две точки в пространстве А и В. Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка [AB] на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: [A 1 B 1]<[AB]; [A 2 B 2]<[AB]; [A 3 B 3]<[AB].
• Обозначим углы между прямой и плоскостями проекций через α- с плоскостью П 1, β- с плоскостью П 2, γ- с плоскостью П 3 и тогда получим: |А 1 В 1| | |cos | 2 2| | |cos | 3 3| | |cos . • Частный случай | 1 1| | 2 2| | 3 3| при таком соотношении прямая образует с плоскостями проекций равные между собой углы =350, при этом каждая из проекций расположена под углом 450 к соответствующим осям проекций. • 2. Двумя плоскостями ( . Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
• • • 3. Двумя проекциями. Пусть в плоскостях П 1 и П 2 даны проекции прямых заданных отрезками А 1 В 1 и 2 2. Проведем через эти прямые плоскости и перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис. а), линией их пересечения будет прямая заданная отрезком АВ , проекциями которой являются отрезки А 1 В 1 и А 2 В 2. а) a непараллельная b б) a и b совпадают Плоскости и могут слиться в одну плоскость , если, например, проекции А 1 В 1 и А 2 В 2 перпендикулярны оси x и пересекают ее в одной точке (рис. б). Прямая линия в этом случае будет однозначно определена своими проекциями, если на каждой из них обозначить две какие-либо точки. Если же обозначений не делать, то за искомую прямую можно принять любую прямую, лежащую в этой плоскости при условии, что она непараллельная ни одной из плоскостей проекций. Точка К, в данном случае - точка пересечения прямой с плоскостью П 2.
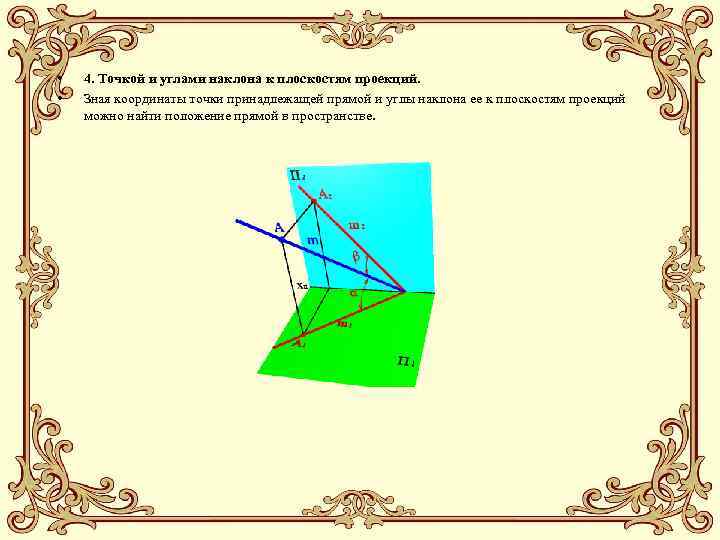• • 4. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.
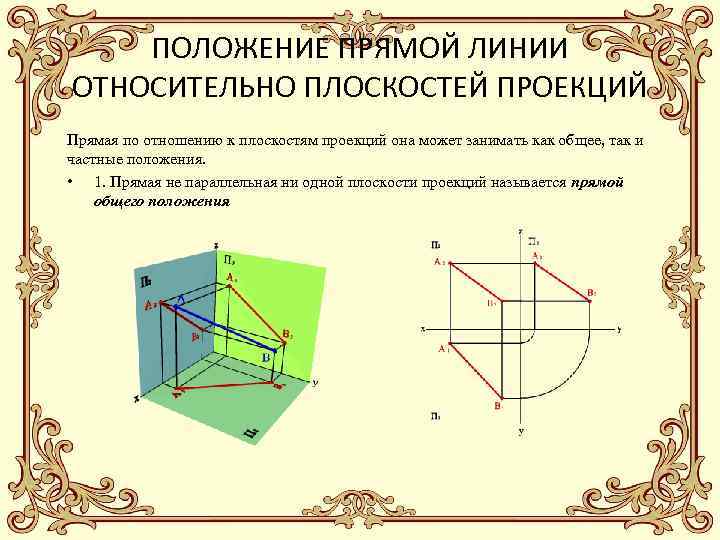ПОЛОЖЕНИЕ ПРЯМОЙ ЛИНИИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения. • 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения
• • 2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают: 2. 1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями. Для любой пары точек горизонтали должно быть справедливо равенство: z. A=z. B Þ A 2 B 2//0 x; A 3 B 3//0 y Þ x. A–x. B≠ 0, y. A–y. B≠ 0, z. A–z. B=0.
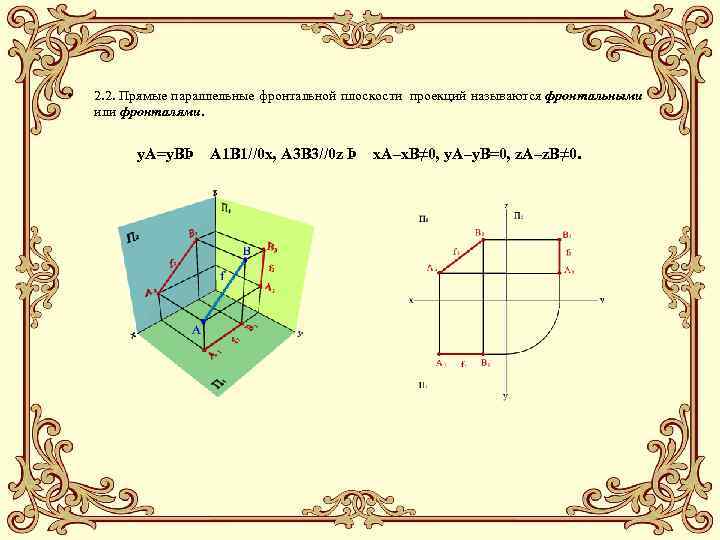• 2. 2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями. y. A=y. BÞ A 1 B 1//0 x, A 3 B 3//0 z Þ x. A–x. B≠ 0, y. A–y. B=0, z. A–z. B≠ 0.
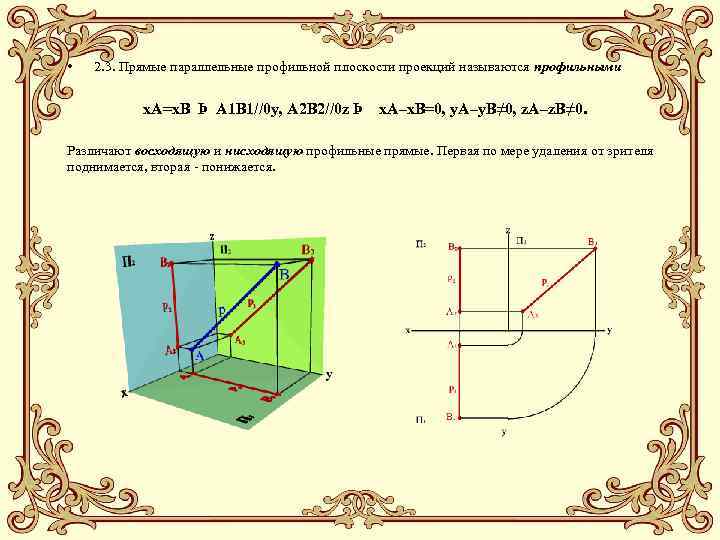• 2. 3. Прямые параллельные профильной плоскости проекций называются профильными x. A=x. B Þ A 1 B 1//0 y, A 2 B 2//0 z Þ x. A–x. B=0, y. A–y. B≠ 0, z. A–z. B≠ 0. Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.
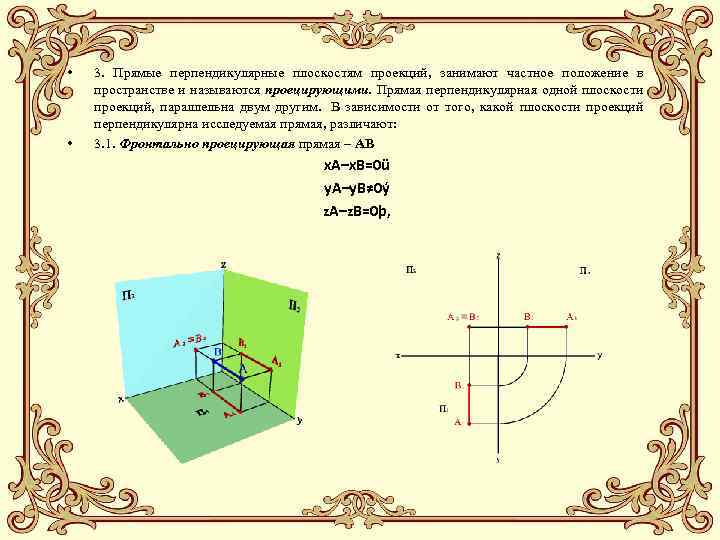• • 3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают: 3. 1. Фронтально проецирующая прямая – АВ x. A–x. B=0ü y. A–y. B≠ 0ý z. A–z. B=0þ,
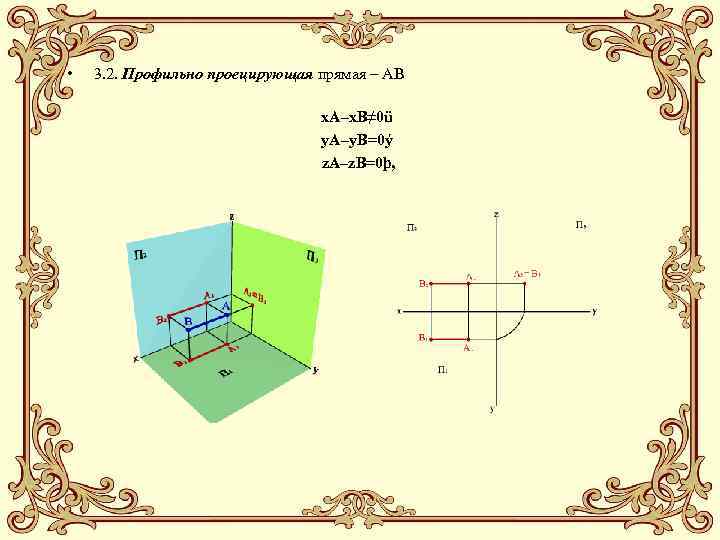• 3. 2. Профильно проецирующая прямая – АВ x. А–x. B≠ 0ü y. А–y. B=0ý z. А–z. B=0þ,
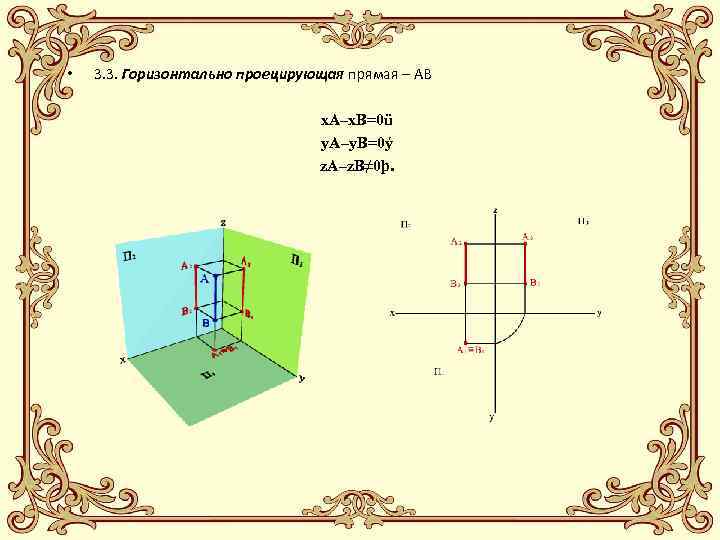• 3. 3. Горизонтально проецирующая прямая – АВ x. А–x. В=0ü y. А–y. В=0ý z. А–z. В≠ 0þ.
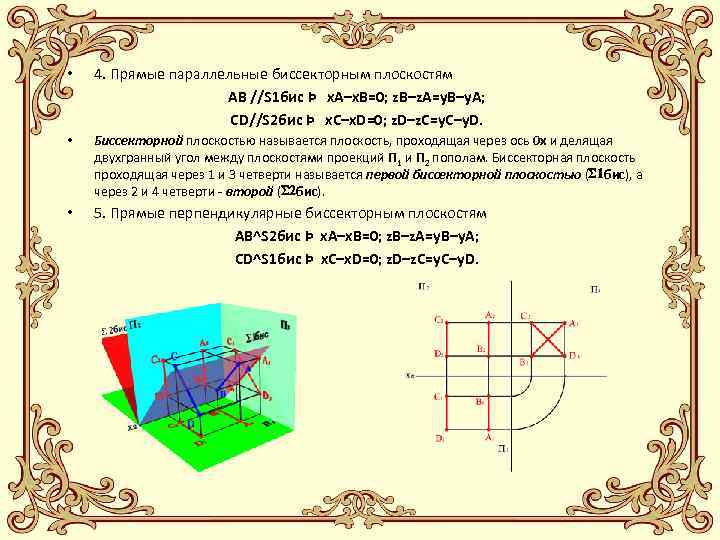• 4. Прямые параллельные биссекторным плоскостям АВ //S 1 бис Þ x. A–x. B=0; z. B–z. A=y. B–y. A; СD//S 2 бис Þ x. С–x. D=0; z. D–z. C=y. C–y. D. • Биссекторной плоскостью называется плоскость, проходящая через ось 0 х и делящая двухгранный угол между плоскостями проекций П 1 и П 2 пополам. Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью ( бис), а через 2 и 4 четверти - второй ( бис). • 5. Прямые перпендикулярные биссекторным плоскостям АВ^S 2 бис Þ x. A–x. B=0; z. B–z. A=y. В–y. А; СD^S 1 бис Þ x. С–x. D=0; z. D–z. C=y. C–y. D.
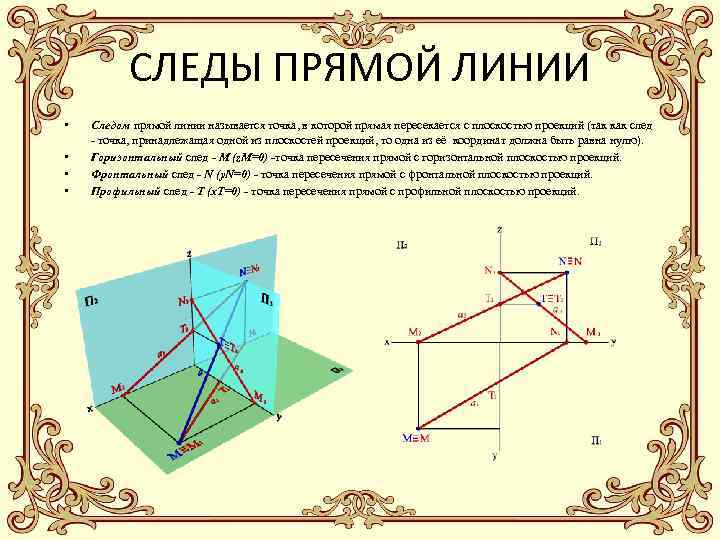СЛЕДЫ ПРЯМОЙ ЛИНИИ • • Следом прямой линии называется точка, в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её координат должна быть равна нулю). Горизонтальный след - М (z. M=0) -точка пересечения прямой с горизонтальной плоскостью проекций. Фронтальный след - N (y. N=0) - точка пересечения прямой с фронтальной плоскостью проекций. Профильный след - Т (x. Т=0) - точка пересечения прямой с профильной плоскостью проекций.
• • • Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с самим следом, а другие проекции лежат на осях. Например, фронтальный след прямой N 2ºN, а N 1 лежит на оси x, N 3 - на оси z. Отмеченные особенности в расположении следов проекций позволяет сформулировать следующие правила: 1. Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью 0 x и в этой точке восстановить перпендикуляр к оси до пересечения с горизонтальной проекцией прямой. 2. Для построения фронтального следа N прямой нужно из точки пересечения горизонтальной проекции её с осью 0 x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.
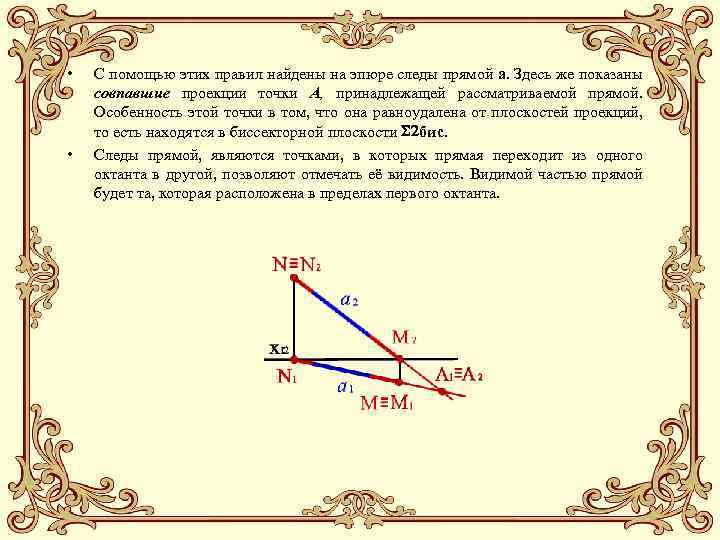• • С помощью этих правил найдены на эпюре следы прямой а. Здесь же показаны совпавшие проекции точки А, принадлежащей рассматриваемой прямой. Особенность этой точки в том, что она равноудалена от плоскостей проекций, то есть находятся в биссекторной плоскости бис. Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.
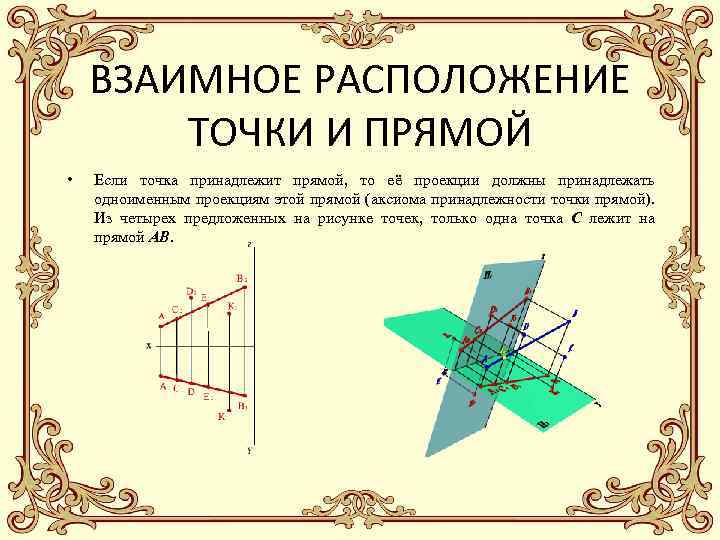ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ И ПРЯМОЙ • Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке точек, только одна точка С лежит на прямой АВ.
• В тех случаях, когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П 1, П 2 и П 3), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П 1, П 2 или П 3. Например, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости проекций • Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении. Зная это условие можно определить принадлежность точки К прямой АВ: • А 2 К 2 /К 2 В 2 ¹А 1 К 1/К 1 В 1 Þ КÏАВ
ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ В ЗАДАННОМ СООТНОШЕНИИ • • Чтобы некоторый отрезок разделить на эпюре в данном соотношении, надо в том же отношении разделить его проекции. Пример: Чтобы разделить отрезок АВ в отношении 2: 3 из точки А 1 проведем произвольный отрезок А 1 В*1 разделенный на 5 -ть равных частей |A 1 K*1|=2 , |K*1 B*1|=3. А 1 К*1/ К*1 В*1=2/3 Соединяя точку В*1 с точкой В 1 и проведя из точки К*1 прямую параллельную (В 1 В*1) получим проекцию точки К 1. Согласно теореме Фалеса (Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону, то на другой стороне отложатся равные между собой отрезки) А 1 К 1/К 1 В 1=2/3 , далее находим К 2 . Таким образом проекции точки К делят одноименные проекции отрезка АВ в данном отношении следовательно и точка К делит отрезок АВ в отношении 2/3.
ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ ЛИНИИ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ (МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА) • Длину отрезка АВ и угол наклона отрезка к плоскости П 1 можно определить из прямоугольного треугольника АВС |AС|=|A 1 B 1|, |BС|=DZ. Для этого на эпюре из точки B 1 под углом 900 проводим отрезок 1* , полученный в результате построений отрезок |B 1 B 1*|=DZ* и будет натуральной величиной отрезка АВ, а угол B 1 A 1 B 1*=a. Рассмотренный метод называется методом прямоугольного треугольника. Тот же результат можно получить при вращении треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П 1, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций» .
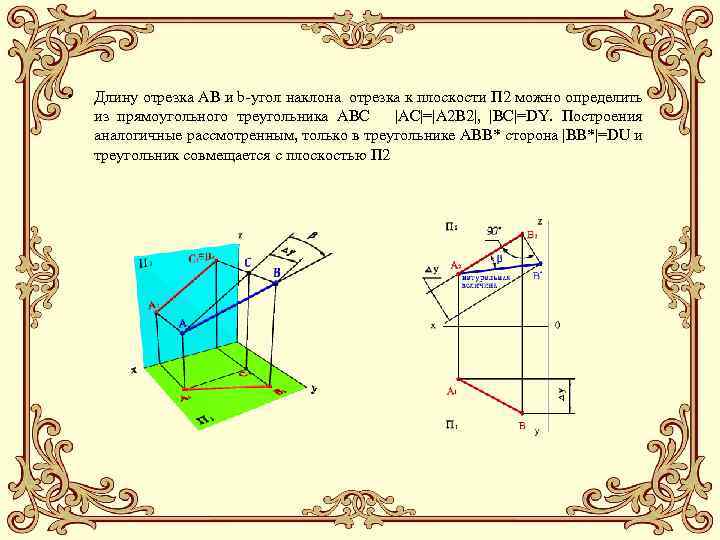• Длину отрезка АВ и b-угол наклона отрезка к плоскости П 2 можно определить из прямоугольного треугольника АВС |AС|=|A 2 B 2|, |BС|=DY. Построения аналогичные рассмотренным, только в треугольнике АВВ* сторона |BВ*|=DU и треугольник совмещается с плоскостью П 2
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ • Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.
1. Параллельные прямые линии. • • Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек. Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если AB CD то A 1 B 1 C 1 D 1; A 2 B 2 C 2 D 2; A 3 B 3 C 3 D 3. В общем случае справедливо и обратное утверждение.
• • Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций. В рассмотренном случае проекции отрезков на плоскость П 3 пересекаются, следовательно, они не параллельны. Решение этого вопроса можно получить сравнением двух соотношений если: А 2 В 2/ А 1 В 1= С 2 Д 2/ С 1 Д 1 АВ//СД А 2 В 2/ А 1 В 1 С 2 Д 2/ С 1 Д 1 АВ СД
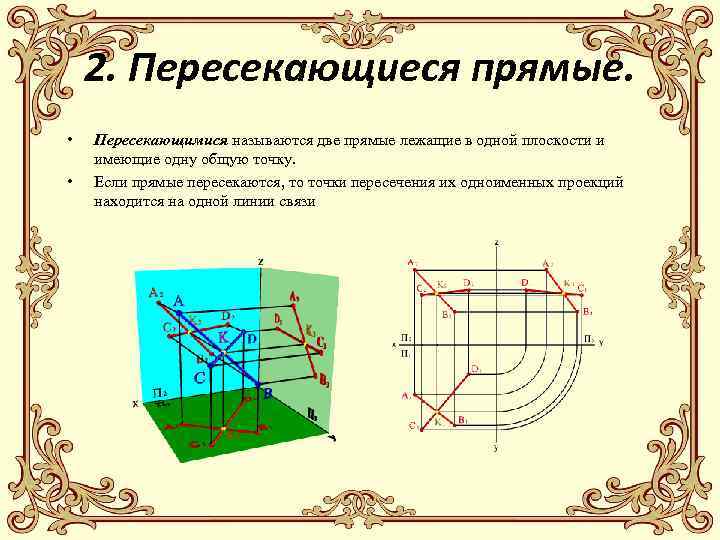2. Пересекающиеся прямые. • • Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку. Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи
• • В общем случае справедливо и обратное утверждение, но есть два частных случая: 1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например, профильной , то по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, однако сами отрезки не пересекаются, потому что точка пересечения профильных проекций этих отрезков не лежит на одной линии связи с точками пересечения их горизонтальной и фронтальной проекций.
• • 2. Пересекающие прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций. О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции (А 1 В 1∩С 1 D 1 АВ∩СD).
3. Скрещивающиеся прямые • • Скрещивающимися называются две прямые не лежащие в одной плоскости. Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи. Точке пересечения фронтальных проекций прямых соответствуют две точки А и В, из которых одна принадлежит прямой а, другая в. Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки А и В находятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точка В, лежащая на прямой в, следовательно, прямая в проходит в этом месте ближе прямой а и фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и D решение аналогично). Этот способ определения видимости по конкурирующим точкам. В данном случае точки А и В- фронтально конкурирующие, а С и D -горизонтально конкурирующие.
ПРОЕКЦИИ ПЛОСКИХ УГЛОВ • Угол - геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. • Углом между прямыми называется меньший из двух смежных углов, лучи которых параллельны этим прямым. • Углом между плоскостью и не перпендикулярной ей прямой называется угол между прямой и её проекцией на данную плоскость.
• • Рассмотрим ряд свойств ортогональных проекций плоских углов: 1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла). Дано: АВС 90 о; ВС // П 1; АС П 1. Для доказательства теоремы продлим отрезок АС до пересечения с плоскостью П 1 получим горизонтальный след прямой - точку М М 1, одновременно принадлежащую прямой и ее проекции. Из условия следует, что ВС // В 1 С 1. Если через точку М проведем прямую МD параллельную С 1 В 1 , то она будет параллельна и СВ, а следовательно СМD 90 о. Согласно теореме о трех перпендикулярах С 1 МD 90 о. Таким образом, [MD]^[А 1 С 1] и [MD]//[В 1 С 1], следовательно, Ð А 1 С 1 В 1= 90 о, что и требовалось доказать. В случае, когда АС ^П 1 проекцией угла, согласно свойствам ортогонального проецирования, будет прямая линия.
• 2. Если проекция угла представляет угол 900, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций • 3. Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу. 4. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве. 5. Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением. • •
