Environmentally Conscious Design Manufacturing Class 24 Optimization

Environmentally Conscious Design & Manufacturing Class 24: Optimization - Operations Research Prof. S. M. Pandit Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 1

Linear Programming • • Problem statement Developing the objective function What are the constraints? Mathematical model Example 1 & 3 from Hamdy A. Taha, “Operations Research” and 2 from Hillier & Lieberman, “Introduction to Operations Research” Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 2

Example 1 of LP Given: • A small paint company produces both interior and exterior house paints for wholesale distribution. • Two raw materials, A & B are used. • The price per ton is $3, 000 for exterior paint and $ 2, 000 for interior paint. Ask: How much interior and exterior paints should the company produce daily to maximize gross income? Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 3

Example 1 of LP Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 4

Construction of the Math. Model • • • What are the variables (unknowns ) of the problem? What constraints must be imposed on the variables to satisfy the limitations of the modeled system? What is the objective (goal) that need to be achieved to determine the optimum (best) solution from among all the feasible values of the variables? Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 5

Variables & Objective Function Variables: x. E=tons produced daily of exterior paint x. I =tons produced daily of interior paint Objective function: z=3 x. E+2 x. I Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 6

Constraints Usage restriction: (raw material A) (raw material B) Demand restriction: (excess of interior over exterior paint) (maximum demand for interior paint) Nonnegativity restriction: Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 7

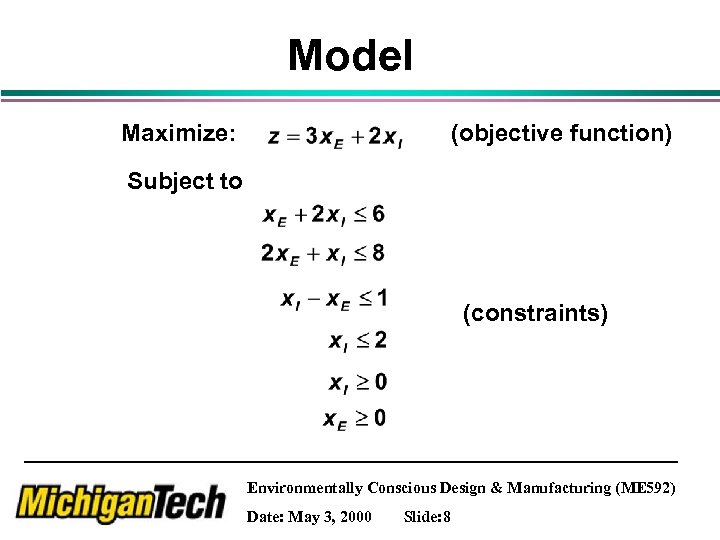Model Maximize: (objective function) Subject to (constraints) Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 8

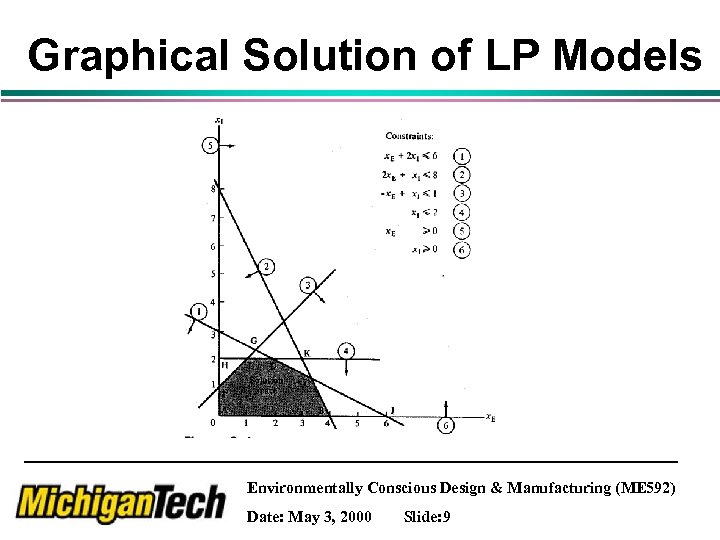Graphical Solution of LP Models Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 9

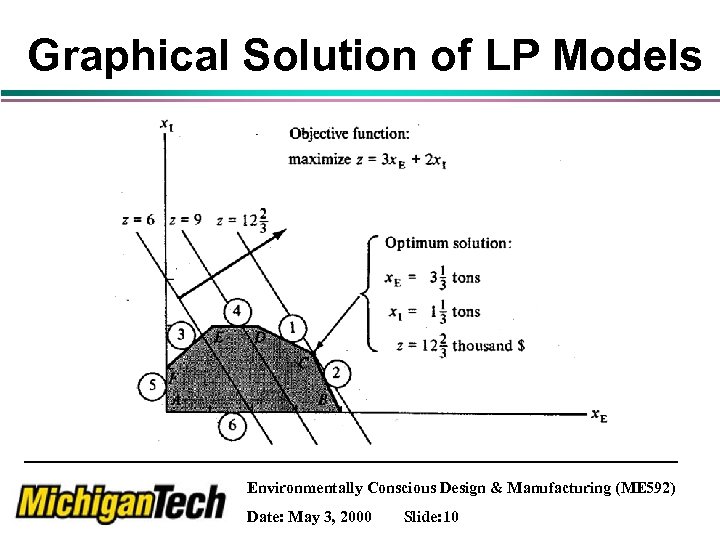Graphical Solution of LP Models Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 10

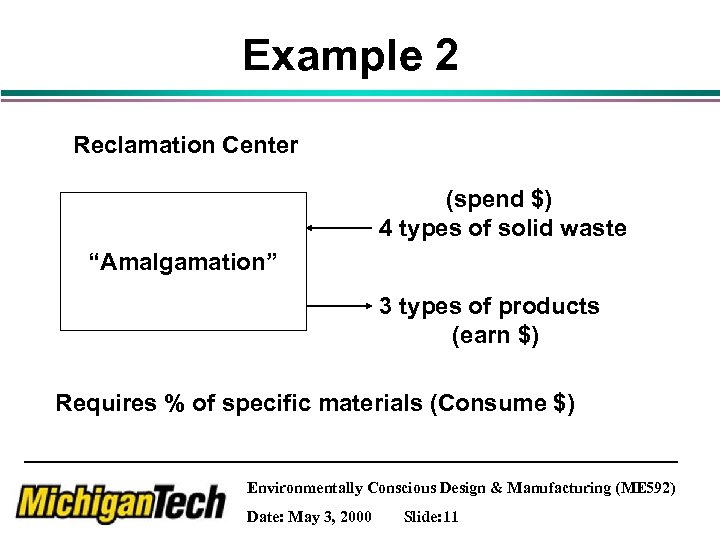Example 2 Reclamation Center (spend $) 4 types of solid waste “Amalgamation” 3 types of products (earn $) Requires % of specific materials (Consume $) Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 11

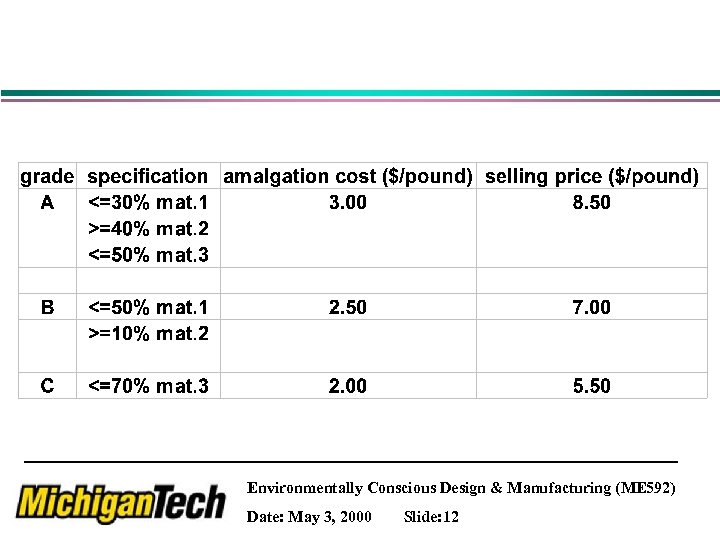Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 12

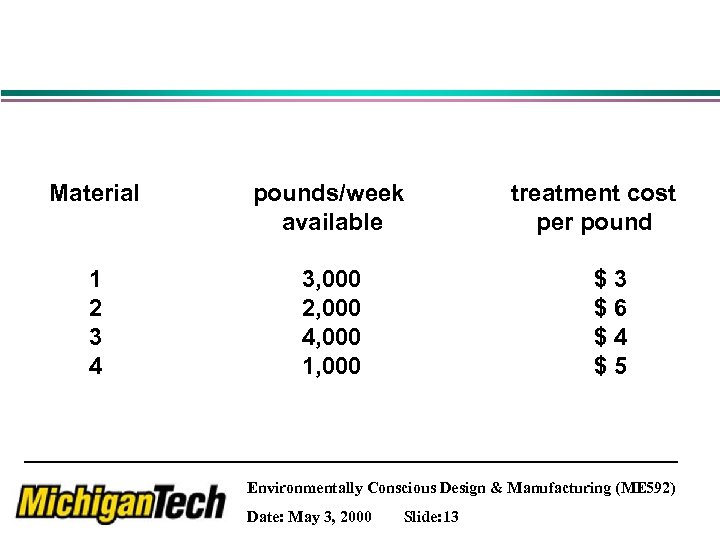Material pounds/week available 1 2 3 4 3, 000 2, 000 4, 000 1, 000 treatment cost per pound $3 $6 $4 $5 Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 13

Formulation Q: What are the decision variables? - What information is needed? - What kind of decision variable(s) would best provide the information needed? Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 14

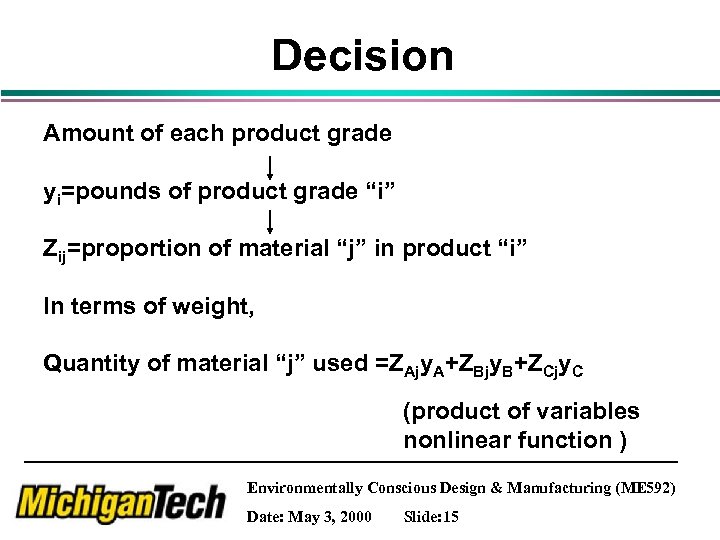Decision Amount of each product grade yi=pounds of product grade “i” Zij=proportion of material “j” in product “i” In terms of weight, Quantity of material “j” used =ZAjy. A+ZBjy. B+ZCjy. C (product of variables nonlinear function ) Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 15

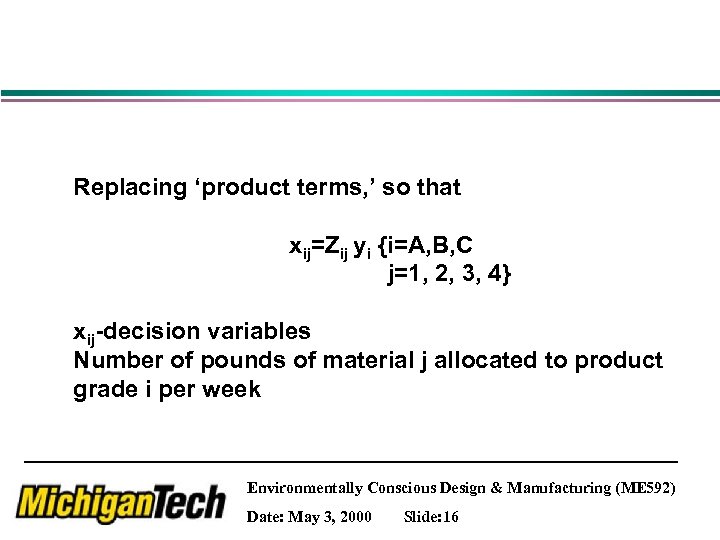Replacing ‘product terms, ’ so that xij=Zij yi {i=A, B, C j=1, 2, 3, 4} xij-decision variables Number of pounds of material j allocated to product grade i per week Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 16

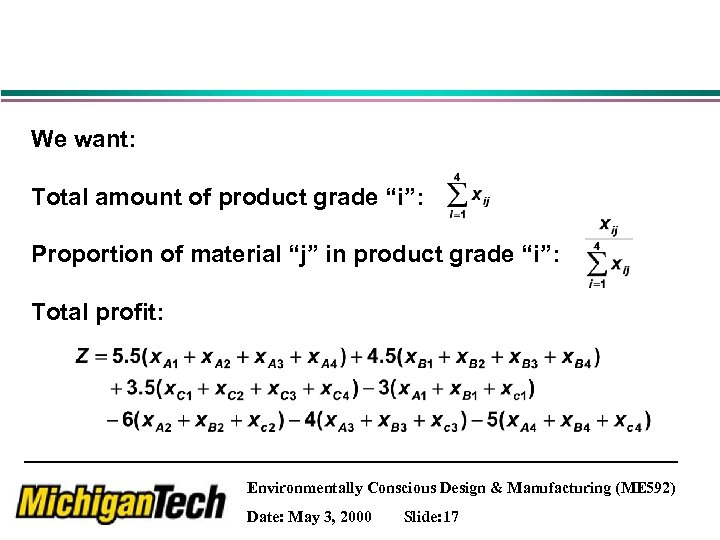We want: Total amount of product grade “i”: Proportion of material “j” in product grade “i”: Total profit: Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 17

Model: Constraints: • • • Availability Mixture specifications Non-negativity Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 18

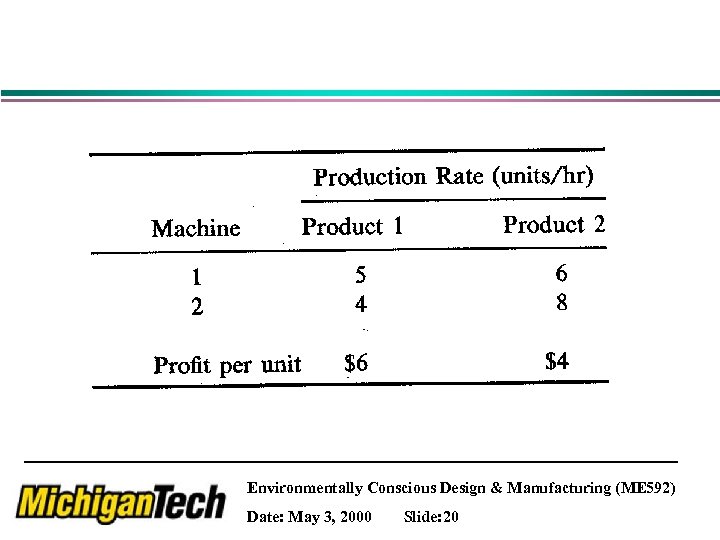
Example 3: Goal Programming Given: • Two products are manufactured by passing sequentially through two different machines • The time available for the two products on each machine is limited to 8 hours daily but may be exceeded by up to 4 hours on an overtime basis • Each overtime hour will cost an additional $ 5 Require • To determine the production level for each product that will maximize the net profit. Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 19

Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 20

Goal Programming The constraints of the model without the overtime option (machine 1) (machine 2) The constraints of the model with the overtime option (machine 1) (machine 2) Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 21

Mathematical Representation To determine the number of units of each product (variables) that maximizes net profit (objective ) provided that the maximum allowable machine hours are exceeded only on an overtime basis (constraints) Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 22

Complete Model Maximize Subject to Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 23

Goal Programming To convert the model to a linear program, we use the substitution which is equivalent to Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 24

LP Model maximize Subject to Environmentally Conscious Design & Manufacturing (ME 592) Date: May 3, 2000 Slide: 25