bfc2b65bd5f7cbd00d8afa5369a075c7.ppt
- Количество слайдов: 27

“Entanglement in Spin & Orbital Systems” Krakow, 18 -22 June 2008 Orbital Order in Titanium and Vanadium Spinels Sergio Di Matteo Équipe de Physique des Surfaces et Interfaces Institut de Physique de Rennes Université de Rennes 1 (France)

In collaboration with: G. Jackeli, N. B. Perkins and C. Lacroix Main publications on the subject: S. Di Matteo, G. Jackeli, C. Lacroix, N. B. Perkins, Physical Review Letters 93, (2004) 077208 Valence bond crystal in a pyrochlore antiferromagnet with orbital degeneracy. S. Di Matteo, G. Jackeli, N. B. Perkins, Physical Review B 72 (2005) 024431 -1 à 15 Valence-bond crystal and lattice distortions in a pyrochlore antiferromagnet with orbital degeneracy. S. Di Matteo, G. Jackeli, N. B. Perkins, Physical Review B 72 (2005) R 020408 Orbital order in vanadium spinels.

Overview of the talk • General considerations • The case of Mg. Ti 2 O 4 • The case of MV 2 O 4 (M=Zn, Mg, Cd) • Conclusions
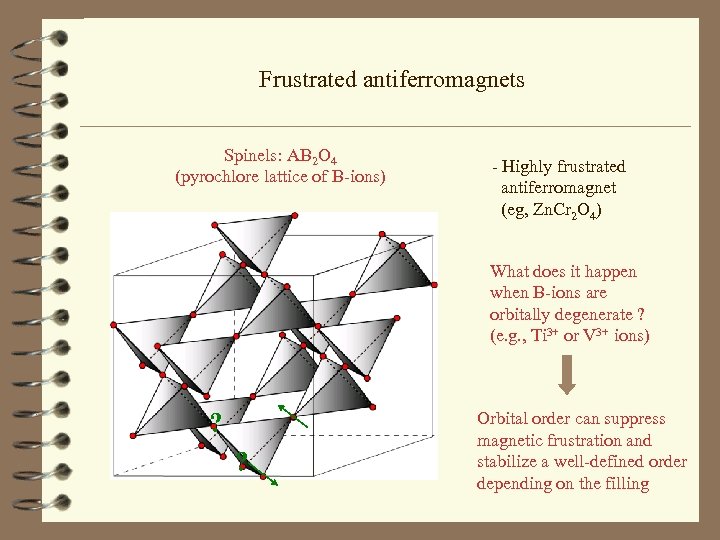
Frustrated antiferromagnets Spinels: AB 2 O 4 (pyrochlore lattice of B-ions) - Highly frustrated antiferromagnet (eg, Zn. Cr 2 O 4) What does it happen when B-ions are orbitally degenerate ? (e. g. , Ti 3+ or V 3+ ions) ? ? Orbital order can suppress magnetic frustration and stabilize a well-defined order depending on the filling

The spinel t 2 g “series” Insulator, Tt=260 K From Isobe and Ueda (J. Phys. Soc. Jpn. 71, 1848 (2002))
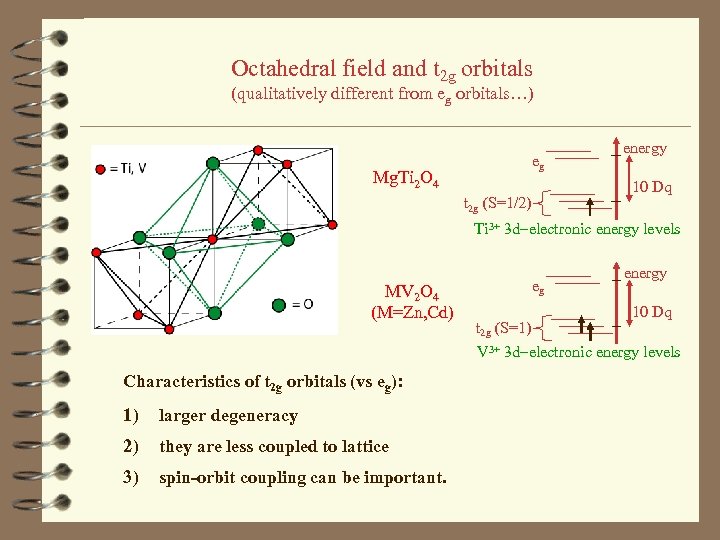
Octahedral field and t 2 g orbitals (qualitatively different from eg orbitals…) eg Mg. Ti 2 O 4 energy 10 Dq t 2 g (S=1/2) Ti 3+ 3 d-electronic energy levels MV 2 O 4 (M=Zn, Cd) Characteristics of t 2 g orbitals (vs eg): 1) larger degeneracy 2) they are less coupled to lattice 3) spin-orbit coupling can be important. eg energy 10 Dq t 2 g (S=1) V 3+ 3 d-electronic energy levels
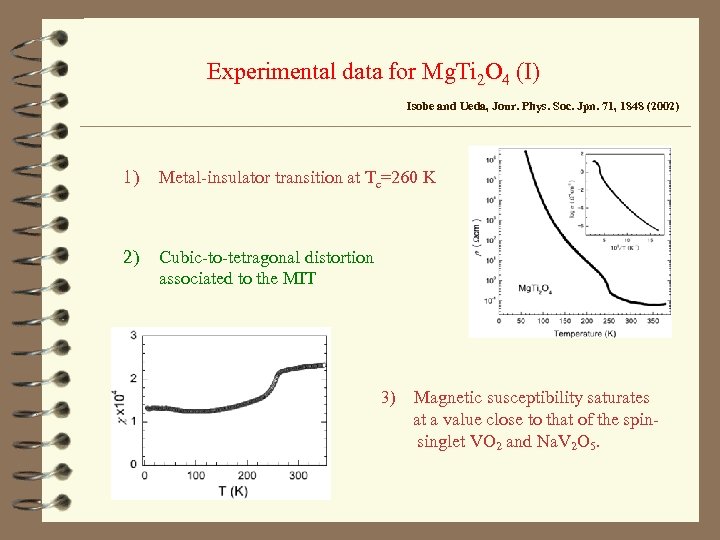
Experimental data for Mg. Ti 2 O 4 (I) Isobe and Ueda, Jour. Phys. Soc. Jpn. 71, 1848 (2002) 1) Metal-insulator transition at Tc=260 K 2) Cubic-to-tetragonal distortion associated to the MIT 3) Magnetic susceptibility saturates at a value close to that of the spinsinglet VO 2 and Na. V 2 O 5.
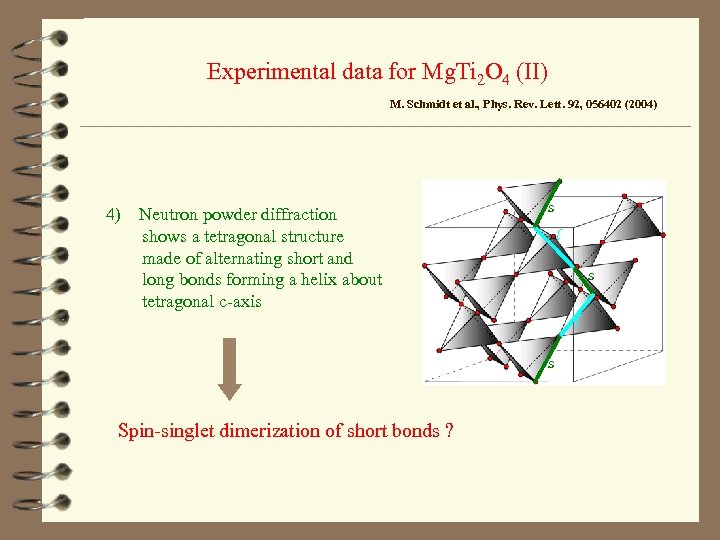
Experimental data for Mg. Ti 2 O 4 (II) M. Schmidt et al. , Phys. Rev. Lett. 92, 056402 (2004) 4) Neutron powder diffraction shows a tetragonal structure made of alternating short and long bonds forming a helix about tetragonal c-axis s l s Spin-singlet dimerization of short bonds ?

Theoretical description: the effective Kugel-Khomskii Hamiltonian 2 nd order perturbation theory in t/U of the multi-orbital single-band Hubbard Hamiltonian : ; For Mg. Ti 2 O 4, tdds = -0. 32 e. V; tddp = 0. 006 e. V; tddd = 0. 11 e. V; We can neglect tddp and tddd compared to tdds

Kugel-Khomskii Hamiltonian with dds-hopping (ddp and ddd neglected) Simplified orbital Hamiltonian : in the plane ab (xy, xz, yz): SE constants: J 1 J(1+ h); J 2 J(1 - h); J 3 4 J(1 - h); Relevant energy scales: J = t 2 / U 2 25 me. V; and h = JH / U 2 0. 15

Kugel-Khomskii Hamiltonian with dds-hopping (ddp and ddd neglected) Simplified orbital Hamiltonian : in the plane ab (xy, xz, yz): SE constants: J 1 J(1+ h); J 2 J(1 - h); J 3 4 J(1 - h); Relevant energy scales: J = t 2 / U 2 25 me. V; and h = JH / U 2 0. 15
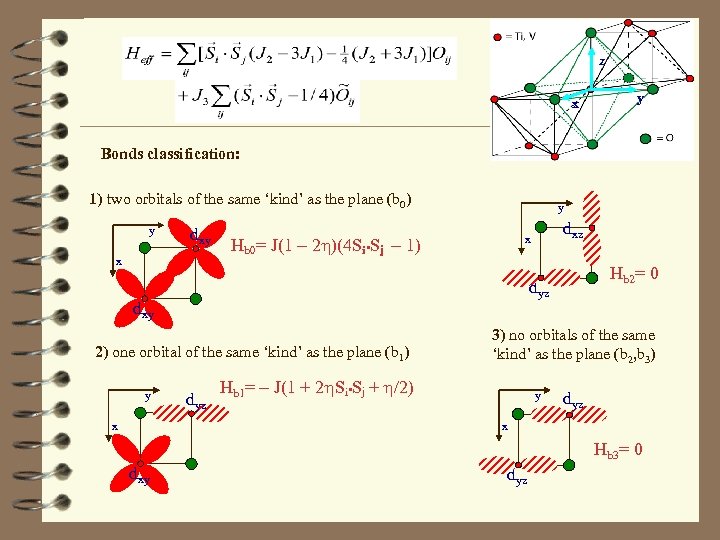
z x y Bonds classification: 1) two orbitals of the same ‘kind’ as the plane (b 0) y dxy x y Hb 0= J(1 - 2 h)(4 Si • Sj - 1) 2) one orbital of the same ‘kind’ as the plane (b 1) x Hb 2= 0 dyz dxy y dxz x dyz 3) no orbitals of the same ‘kind’ as the plane (b 2, b 3) Hb 1= - J(1 + 2 h. Si • Sj + h/2) y dyz x Hb 3= 0 dxy dyz
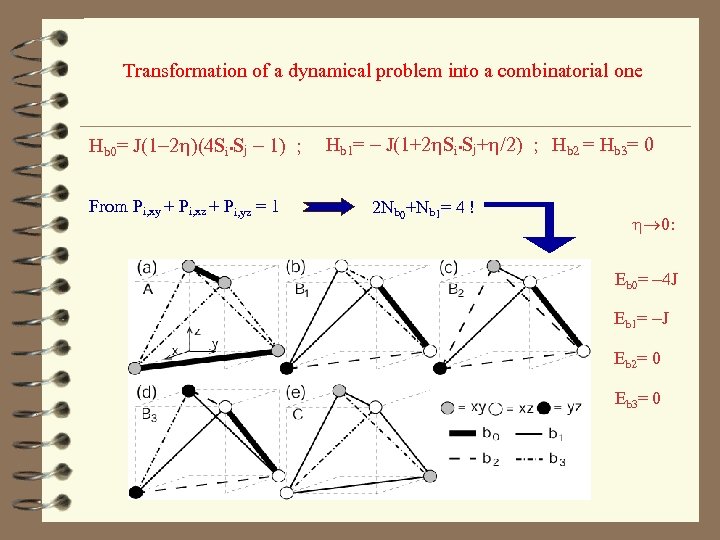
Transformation of a dynamical problem into a combinatorial one Hb 0= J(1 -2 h)(4 Si • Sj - 1) ; From Pi, xy + Pi, xz + Pi, yz = 1 Hb 1= - J(1+2 h. Si • Sj+h/2) ; Hb 2 = Hb 3= 0 2 Nb 0+Nb 1= 4 ! h 0: Eb 0= -4 J Eb 1= -J Eb 2= 0 Eb 3= 0
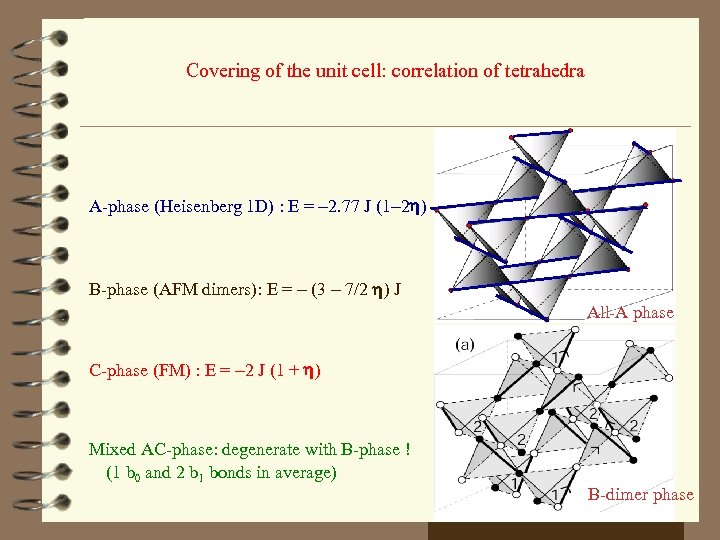
Covering of the unit cell: correlation of tetrahedra A-phase (Heisenberg 1 D) : E = -2. 77 J (1 -2 h) B-phase (AFM dimers): E = - (3 - 7/2 h) J All-A phase C-phase (FM) : E = -2 J (1 + h) Mixed AC-phase: degenerate with B-phase ! (1 b 0 and 2 b 1 bonds in average) B-dimer phase
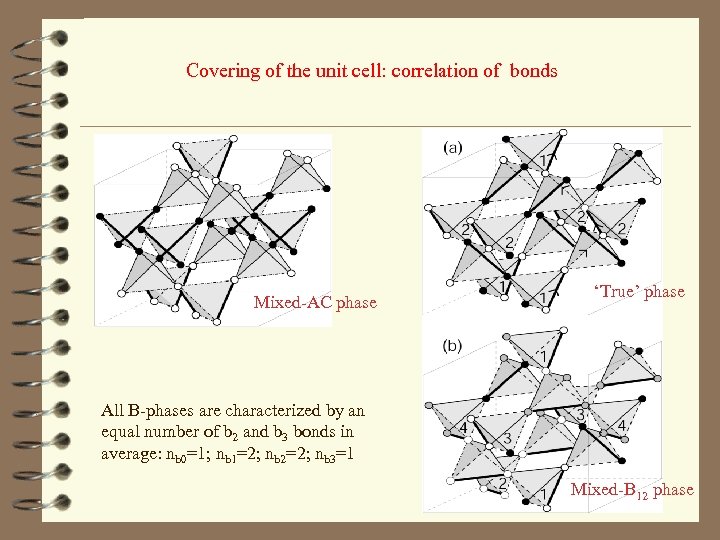
Covering of the unit cell: correlation of bonds Mixed-AC phase ‘True’ phase All B-phases are characterized by an equal number of b 2 and b 3 bonds in average: nb 0=1; nb 1=2; nb 2=2; nb 3=1 Mixed-B 12 phase
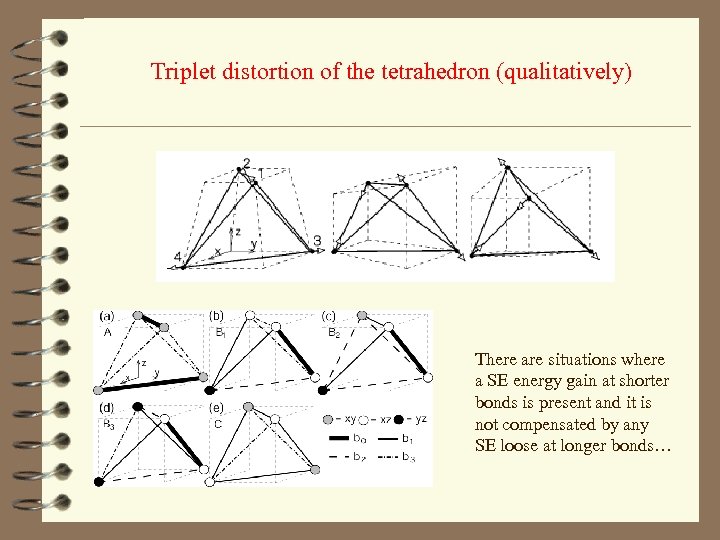
Triplet distortion of the tetrahedron (qualitatively) There are situations where a SE energy gain at shorter bonds is present and it is not compensated by any SE loose at longer bonds…
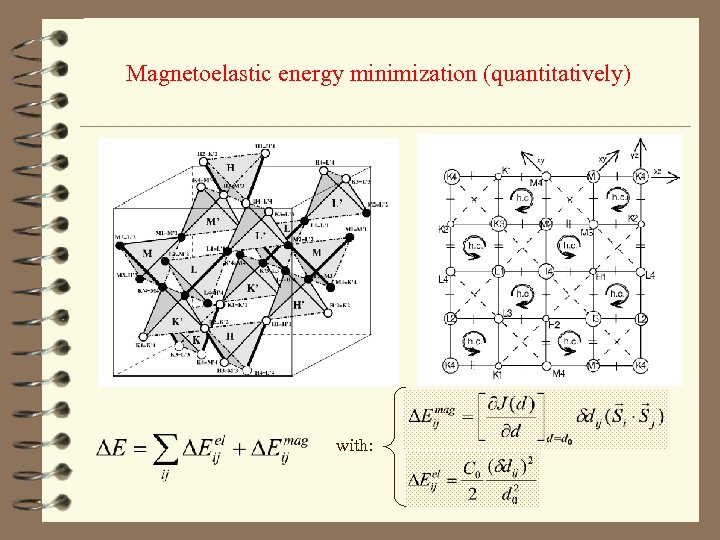
Magnetoelastic energy minimization (quantitatively) with:
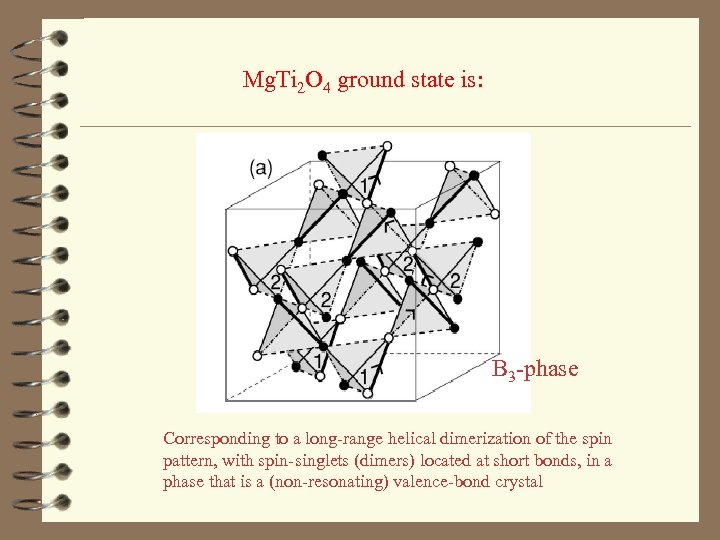
Mg. Ti 2 O 4 ground state is: B 3 -phase Corresponding to a long-range helical dimerization of the spin pattern, with spin-singlets (dimers) located at short bonds, in a phase that is a (non-resonating) valence-bond crystal

Experimental data for Zn. V 2 O 4 S. -H. Lee et al. , Phys. Rev. Lett. 93, 156407 (2004) M. Reehuis et al. , Eur. Phys. Jour. B 35, 311 (2003) M. Onoda & J. Hasegawa, JPCM 15, L 95 (2003) 1) Two very close transition temperatures: a structural one (cubic-to-tetragonal) at Tc=52 K and a (3 D) AFM one at TN=44 K (and similar for Cd. V 2 O 4 and Mg. V 2 O 4) 2) An AFM (Néel) 1 D order, along the directions [110], [110] with a saturated moment m=0. 6 m. B, directed along the [001] direction between the two transition temperatures. 3) A tetragonal space group (I 41/amd) apparently at odds with the marked anisotropy in the structure factor S(Q)…
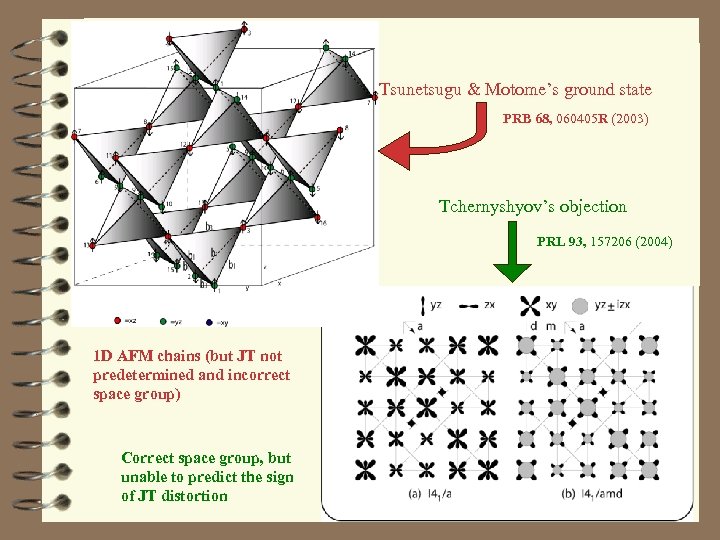
Tsunetsugu & Motome’s ground state PRB 68, 060405 R (2003) Tchernyshyov’s objection PRL 93, 157206 (2004) 1 D AFM chains (but JT not predetermined and incorrect space group) Correct space group, but unable to predict the sign of JT distortion
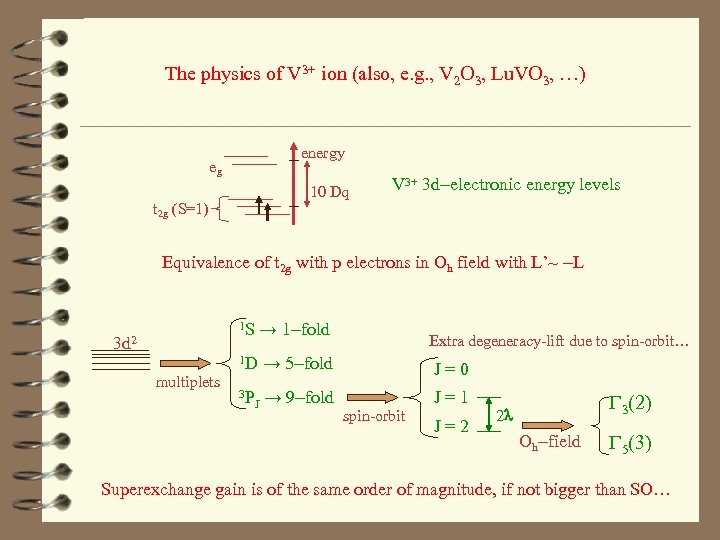
The physics of V 3+ ion (also, e. g. , V 2 O 3, Lu. VO 3, …) energy eg 10 Dq t 2 g (S=1) V 3+ 3 d-electronic energy levels Equivalence of t 2 g with p electrons in Oh field with L’~ -L 1 S → 1 -fold 3 d 2 multiplets Extra degeneracy-lift due to spin-orbit… 1 D → 5 -fold J = 0 3 P J = 1 J → 9 -fold spin-orbit J = 2 G 3(2) 2 l Oh-field G 5(3) Superexchange gain is of the same order of magnitude, if not bigger than SO…

The case of Cd. V 2 O 4: the effective SE+SO Hamiltonian (only dds-hoppings: ddp and ddd neglected) with: (for holes !) With J 1 = J h/(1 -3 h); J 2 = J (1 -h)/(1 -3 h); J 3 = J (1+h)/(1+2 h); and h=JH/U 1 0. 10 ; J=t 2/U 1 10 me. V ; l > 0 (e. g. , 13 me. V ) L’ acts in an effective L = 1 subspace spanned by t 2 g states fundamental the relative ratios l/J & h !


The case of Cd. V 2 O 4: the effective SE+SO Hamiltonian (only dds-hoppings: ddp and ddd neglected) with: (for holes !) With J 1 = J h/(1 -3 h); J 2 = J (1 -h)/(1 -3 h); J 3 = J (1+h)/(1+2 h); and h=JH/U 1 0. 10 ; J=t 2/U 1 10 me. V ; l > 0 (e. g. , 13 me. V ) L’ acts in an effective L = 1 subspace spanned by t 2 g states fundamental the relative ratios l/J & h !
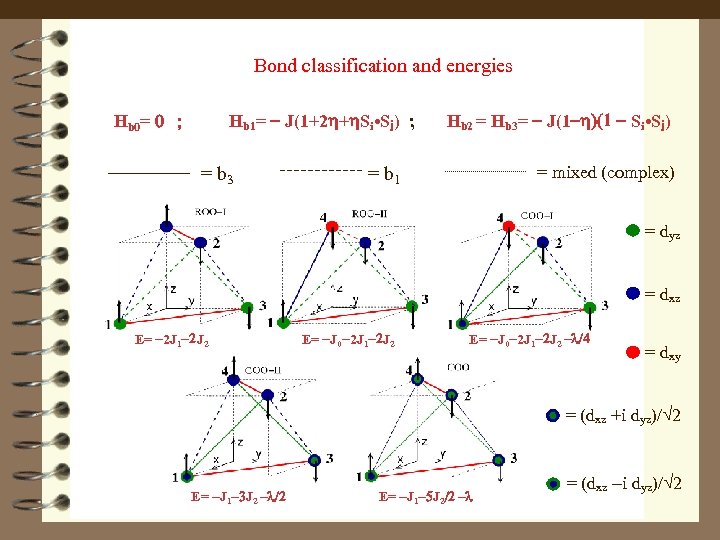
Bond classification and energies Hb 1= - J(1+2 h+h. Si • Sj) ; Hb 0= 0 ; = b 3 Hb 2 = Hb 3= - J(1 -h)(1 - Si • Sj) = mixed (complex) = b 1 C = dyz = dxz E= -2 J 1 -2 J 2 E= -J 0 -2 J 1 -2 J 2 -l/4 = dxy C = (dxz +i dyz)/ 2 E= -J 1 -3 J 2 -l/2 E= -J 1 -5 J 2/2 -l = (dxz -i dyz)/ 2
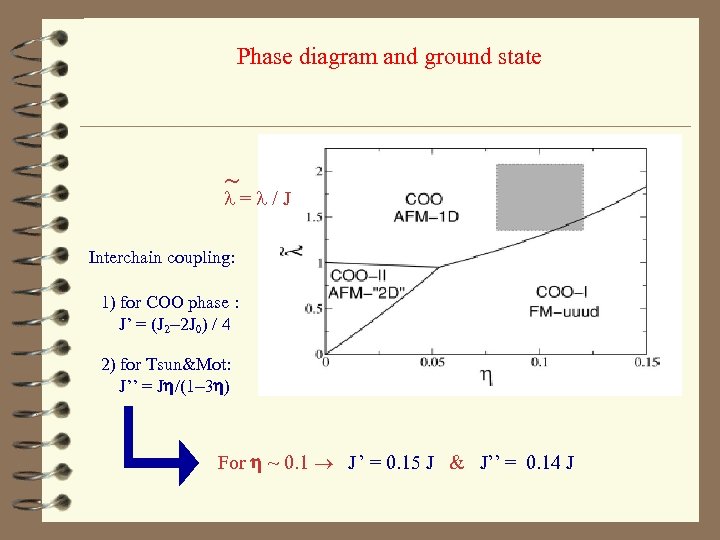
Phase diagram and ground state ~ l = l / J Interchain coupling: 1) for COO phase : J’ = (J 2 -2 J 0) / 4 2) for Tsun&Mot: J’’ = Jh/(1 -3 h) For h ~ 0. 1 J ’ = 0. 15 J & J’’ = 0. 14 J

Conclusions: 1) The different behavior of Mg. Ti 2 O 4 (spin-dimers, ROO) and of Cd. V 2 O 4 (1 D Heisenberg AFM, COO) can be ascribed to the different filling (2 1 !). 2) Particularly for Mg. Ti 2 O 4, where we could solve our electronic model exactly, the agreement with the experimental data is satisfying. 3) In spite of these results, I have a negative remark: theory is still too much at the level of a “art” (no easy protocol to follow) and the physical intuition is still too dependent on known experimental results (no strict predictability).
bfc2b65bd5f7cbd00d8afa5369a075c7.ppt