ENM 503 Block 1 Algebraic Systems Lesson 5

ENM 503 Block 1 Algebraic Systems Lesson 5 – Algebraic Models Relive those old college algebra days when solving an equation was child’s play … 1

The Road Ahead… is not always linear n n n Mall Mart Discount Stores Modeling inventory The algebra of high finances Breaking even The functions of production Solving problems the old fashion way – with algebra 2

Mall Mart Discount Stores n Mall Mart is a national discount retail merchandising company whose stores are located in large population centers near shopping malls. Mall Mart’s policy is to locate a store only in cities having a population of at least 500, 000. Because of the lead time needed for purchasing land, building permits, construction, etc. , Mall Mart must begin the process several years before a store will be open to the public. 3

Mall Mart Discount Stores n n Mathville is a modest Ohio town with a population of 427, 400. Mall Mart has targeted a new store for this town once the population reaches 500, 000. Historically its birth rate has been. 031 births person per year and its death rate has been. 011 deaths person per year. n n There is no significant migration into or out of Mathville expected over the next several years. In how many years should the new Mathville Mall Mart store be programmed for opening? 4

Mall Mart - Models Let P(t) = size of the population in year t, current year t = 0 B(t) = births in year t D(t) = deaths in year t Assumptions: 1. B(t) / P(t) = b, a constant birth rate 2. D(t)/ P(t) = d, a constant death rate 3. no migration 5

Mall Mart - Models B(t) / P(t) = b, birth rate D(t)/ P(t) = d, death rate Model: P(t+1) = P(t) + B(t) – D(t) = P(t) + b. P(t) –d. P(t) = (1 + b –d ) P(t) = r P(t) where r = (1 + b –d) is the growth rate Since P(1) = r P(0) P(2) = r. P(1) = r 2 P(0), etc. , Then P(t) = P(0) rt , an exponential function 6

Solving the Mall Mart Model Growth rate: r = 1 +. 031 -. 011 = 1. 02 P(t) = 1. 02 t P(0) = 500, 000, find t! 1. 02 t = 500, 000 / P(0) = 500, 000 / 427, 400 = 1. 169864296 ln(1. 02 t) = t ln(1. 02) = ln(1. 169864296) t = ln(1. 169864296) / ln(1. 02) = 7. 92 years 7

More Mall Mart Models n If it takes Mall Mart an average of 3. 5 years to complete a new store once the decision is made, at what population size should the decision be made so that the population will have reached 500, 000 at the store opening? The Model: P(t) = P(0) rt The Method: Find P(0) = 500, 000 / r 3. 5 The Math. Ville answer: P(0) = 500, 000 / 1. 023. 5 = 466, 519 8

Much More Mall Mart Models Assume birth and death rates are not constant but are changing over time. Let P(t) = size of the population in year t, current year t = 0 B(t) = births in year t D(t) = deaths in year t Assumptions: 1. Birth rate is linear 2. Death rate is linear 9

Much More Mall Mart Models or M 5 Model: B(t) / P(t) = a – bt (linearly decreasing) D(t) / P(t) = c(t+1) (linearly increasing) P(t+1) = P(t) + B(t) – D(t) P(t+1) = P(t) + {[a – bt] – c(t+1)} P(t) = [1 + a – bt – c(t+1)] P(t) = r(t)P(t) where r(t) = 1 + a – bt – c(t+1) = 1 + (a-c) – (b+c)t P(1) = r(0) P(2) = r(1) P(1) = r(1)r(0)P(0) P(3) = r(2) P(2) = r(2)r(1)P(1) = r(2)r(1)r(0)P(0) 10

Another Mall Mart problem The town of Putrid, Ohio has been experiencing a decrease in its “live” birthrate and an increase in its death rate every since the Dandy Incinerator and Environmental (DIE) Company built its new facility for treating and disposing of toxic waste, nuclear material, asbestos, pesticides, and women’s perfume. Putrid currently “enjoys” a population of 1, 340, 011. Its birth rate this year (t = 0) is. 03 (a) and death rate is. 02 (c) with the birth rate decreasing at. 005 (b) per year. Mall Mart, in keeping with its policy, plans to close its Putrid Store once the town’s population reaches 500, 000. In what year should they plan to close? 11

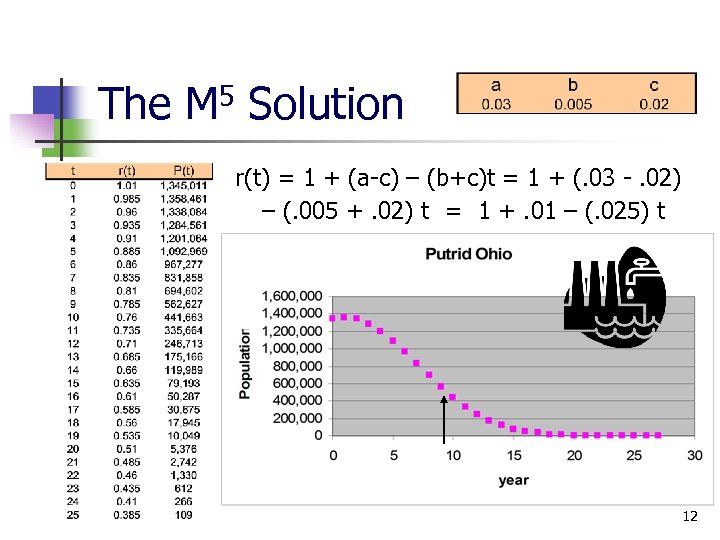
The M 5 Solution r(t) = 1 + (a-c) – (b+c)t = 1 + (. 03 -. 02) – (. 005 +. 02) t = 1 +. 01 – (. 025) t 12

A Descriptive Inventory Model - 1 n n n Among the many items sold at House Depot is a popular electric drill. The daily demand for this drill is a fairly constant 2 per day. How many drills should House Depot stock assuming no backorders (unfilled demands) are permitted? It costs $25 to place an order for one or more drills with the manufacturer. This cost includes the salaries of the individuals completing the purchase order and follow-up actions including paying the bill. One possibility is to order 2 every day resulting in an annual order cost of $25 x 365 = $9, 125. 13

A Descriptive Inventory Model - 2 n n Alternatively, the store could place one order for the year at an ordering cost of $25 per year. However, the drill cost House Depot $35 each. House Depot could invest that money for one year and enjoy a 6 percent return (. 06 x 35 = $2. 10 per item per yr). n n In addition, there are storage, insurance, and pilferage costs. Assume the total holding or carrying costs amount to $3. 00 a year per drill. 14

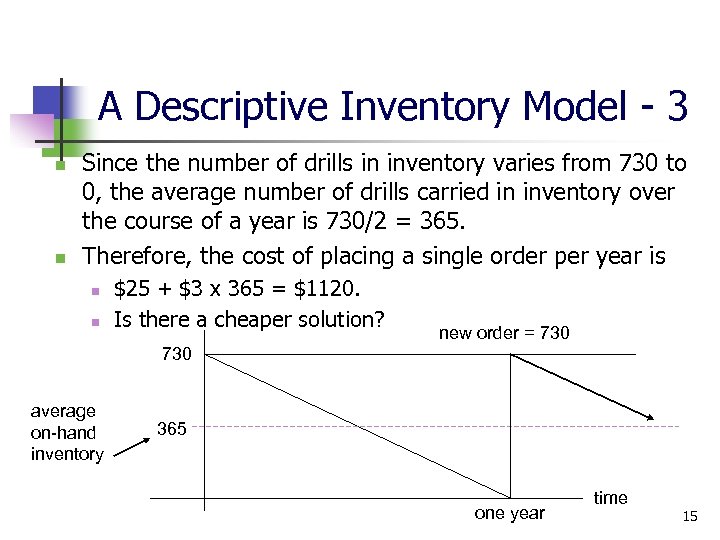
A Descriptive Inventory Model - 3 n n Since the number of drills in inventory varies from 730 to 0, the average number of drills carried in inventory over the course of a year is 730/2 = 365. Therefore, the cost of placing a single order per year is n n $25 + $3 x 365 = $1120. Is there a cheaper solution? new order = 730 average on-hand inventory 365 one year time 15

The Search for a cheaper solution – our model Let n n x = number of units to order (order quantity) y = annual inventory cost = order cost + carrying cost number of orders per yr average on-hand inventory 16

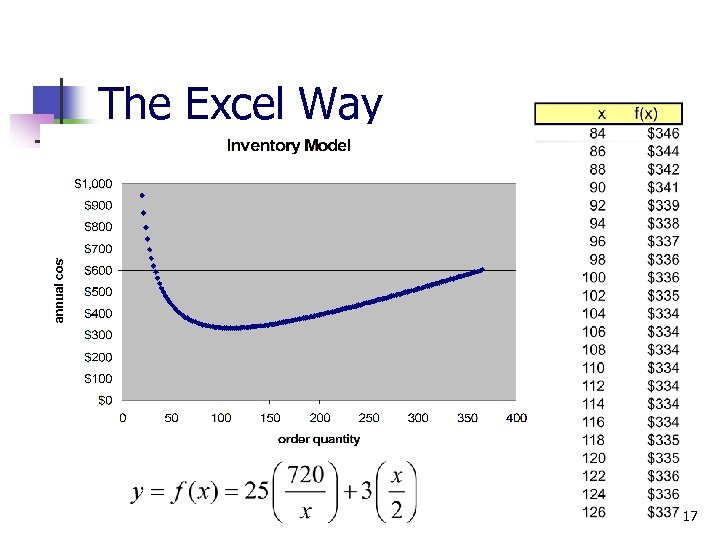
The Excel Way 17

Mathematics of Finance see Chapter 5 18

Compound Interest – exponential functions (life cycle costing, cost benefit analysis, cost trade-offs) S is the money accumulated (future sum) P is the principal (beginning) amount (present value) r is the annual interest rate n is the number of compounding periods per year t is the number of years It’s like your money grows on trees 19

How long to accumulate S dollars? 20

An Example: S = $40, 000 I can’t wait that long! 21

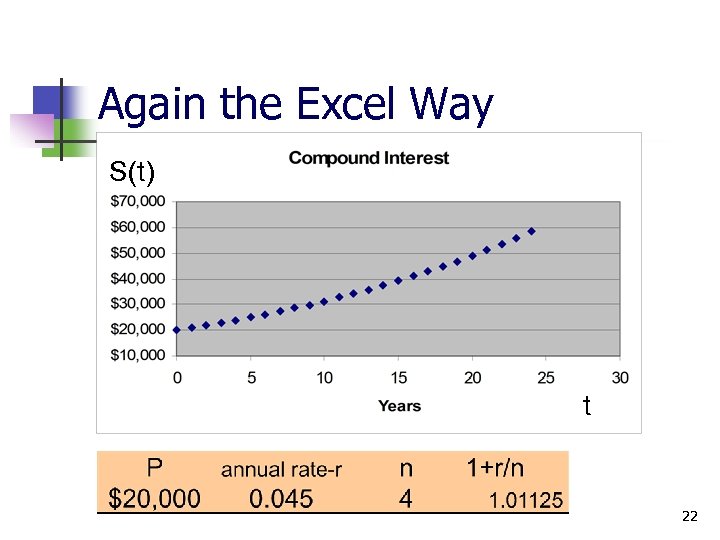
Again the Excel Way S(t) t 22

Solving equations – the break even point Let x = number of units produced and sold (demand) s = unit selling price where x = f(s) r = revenue = sx c = cost = a + bx p = profit = r – c Define the breakeven point: revenue - cost = profit = 0 x Assume d 1 23 s

Solving systems of equations – the break-even point An even break Solve for x using the Quadratic formula 24

Production Functions A production function expresses the relationship between an organization's inputs and its outputs. It indicates, in mathematical or graphical form, what outputs can be obtained from various amounts and combinations of factor inputs. In its most general mathematical form, a production function is expressed as: Q = f(X 1, X 2, X 3, . . . , Xn) where: Q = quantity of output and X 1, X 2, X 3, . . . , Xn = factor inputs (such as capital, labor, raw materials, land, technology, or management) 25

Production Functions There are several ways of specifying this function. One is as an additive production function: Q = a + b. X 1 + c. X 2 + d. X 3, . . . where a, b, c, and d are parameters that are determined empirically. Another is as a Cobb-Douglas production function Q = f(L, K, M) = A * (Lalpha) * (Kbeta) * (Mgamma) where L = labor, K = capital, M = materials and supplies, and Q = units of product. 26

Cobb-Douglas Production Function Q = f(L, K, M) = A * (Lalpha) * (Kbeta) * (Mgamma). Properties of the Cobb-Douglas production function: Decreasing returns to scale: alpha + beta + gamma < 1 Increasing returns to scale: alpha + beta + gamma > 1 Let CL, CK, and CM = the unit cost of labor, capital, and material, then C(L, K, M) = CLL + CKK + CM M is the total cost function 27

A Little Production An interesting problem: Given a monthly budget of $B, how should the money be spent to I know I can obtain a specified output Q? work this one. Q = f(L, K, M) = A * (Lalpha) * (Kbeta) * (Mgamma) C(L, K, M) = CLL + CKK + CM M = $B find L, K, and M! 28

Next Block: We begin our study of Linear Models Two engineering management students caught in a personal show of jubilance over the just ended ENM 503 class. 29