2a98ca530cd8d3ea0c7ea26544cc85e6.ppt
- Количество слайдов: 53
 Enhancing Program Verification with Lemmas (in Separation Logic) Huu Hai Nguyen Wei-Ngan Chin Dept of Computer Science National Univ. of Singapore 1
Enhancing Program Verification with Lemmas (in Separation Logic) Huu Hai Nguyen Wei-Ngan Chin Dept of Computer Science National Univ. of Singapore 1
 Overview • Program verification is a challenging problem. • Balance between expressivity & automation. • Two sources of creative help from users: • • • Pre/post conditions (for methods/loops) Lemmas (for predicates used) Our Approach : Deductive reasoning using separation logic (with inductive help). 2
Overview • Program verification is a challenging problem. • Balance between expressivity & automation. • Two sources of creative help from users: • • • Pre/post conditions (for methods/loops) Lemmas (for predicates used) Our Approach : Deductive reasoning using separation logic (with inductive help). 2
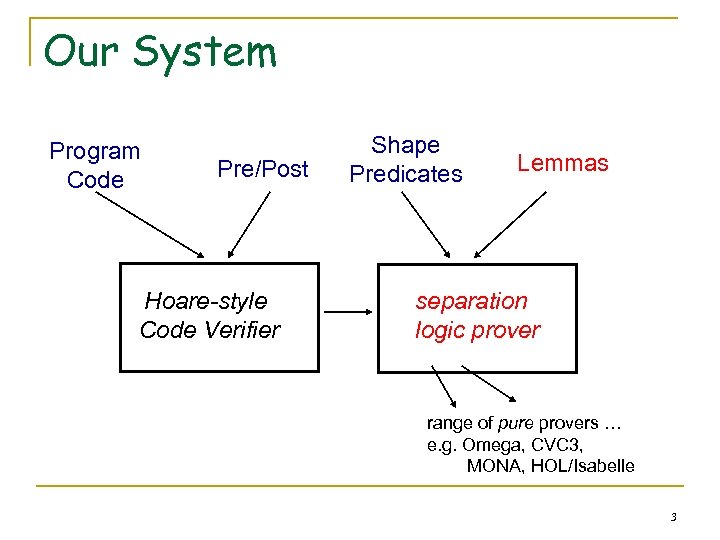 Our System Program Code Pre/Post Hoare-style Code Verifier Shape Predicates Lemmas separation logic prover range of pure provers … e. g. Omega, CVC 3, MONA, HOL/Isabelle 3
Our System Program Code Pre/Post Hoare-style Code Verifier Shape Predicates Lemmas separation logic prover range of pure provers … e. g. Omega, CVC 3, MONA, HOL/Isabelle 3
 Our Work • Lemmas themselves are nothing new. • Contributions: • Support user-specified lemmas (in separation logic) • • • Automatic application of lemmas (goal-directed) Automatic proving of lemmas (cyclic proofs) Soundness and Termination. 4
Our Work • Lemmas themselves are nothing new. • Contributions: • Support user-specified lemmas (in separation logic) • • • Automatic application of lemmas (goal-directed) Automatic proving of lemmas (cyclic proofs) Soundness and Termination. 4
 Outline • • Motivation Background Entailment Lemmas Soundness Experiments Conclusion 5
Outline • • Motivation Background Entailment Lemmas Soundness Experiments Conclusion 5
 Separation Logic • • Extension to Hoare logic to reason about shared mutable data structures. Foundations • • O’Hearn and Pym, “The Logic of Bunched Implications”, Bulletin of Symbolic Logic 1999 Reynolds, “Separation Logic: A Logic for Shared Mutable Data Structures”, LICS 2002 : spatial conjunction -- : spatial implication 6
Separation Logic • • Extension to Hoare logic to reason about shared mutable data structures. Foundations • • O’Hearn and Pym, “The Logic of Bunched Implications”, Bulletin of Symbolic Logic 1999 Reynolds, “Separation Logic: A Logic for Shared Mutable Data Structures”, LICS 2002 : spatial conjunction -- : spatial implication 6
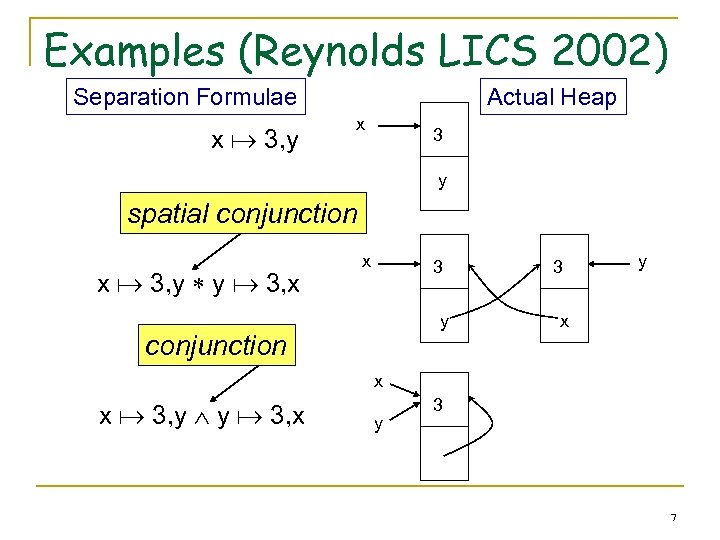 Examples (Reynolds LICS 2002) Separation Formulae x 3, y Actual Heap x 3 y spatial conjunction x 3, y y 3, x x 3 y conjunction 3 y x x x 3, y y 3, x y 3 7
Examples (Reynolds LICS 2002) Separation Formulae x 3, y Actual Heap x 3 y spatial conjunction x 3, y y 3, x x 3 y conjunction 3 y x x x 3, y y 3, x y 3 7
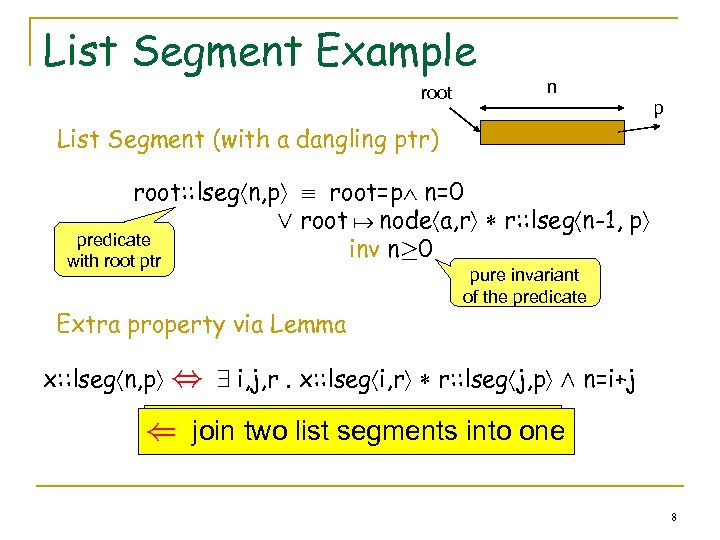 List Segment Example root n p List Segment (with a dangling ptr) root: : lseg n, p root=p n=0 Ç root node a, r r: : lseg n-1, p predicate inv n¸ 0 with root ptr Extra property via Lemma pure invariant of the predicate x: : lseg n, p , 9 i, j, r. x: : lseg i, r r: : lseg j, p Æ n=i+j ) break a list segment into one ( join two list segmentsinto two 8
List Segment Example root n p List Segment (with a dangling ptr) root: : lseg n, p root=p n=0 Ç root node a, r r: : lseg n-1, p predicate inv n¸ 0 with root ptr Extra property via Lemma pure invariant of the predicate x: : lseg n, p , 9 i, j, r. x: : lseg i, r r: : lseg j, p Æ n=i+j ) break a list segment into one ( join two list segmentsinto two 8
 Another Example • Sorted List with min/max and size. sortl n, min, max root: : node min, null min=max Æ n=1 root node min, q q: : sortl n-1, k, max min k inv n 1 Æ min·max Æ root!=null • Another lemma: x: : sortl n, min, max ) x: : lseg n, null Lemma is required for bubble sorting. 9
Another Example • Sorted List with min/max and size. sortl n, min, max root: : node min, null min=max Æ n=1 root node min, q q: : sortl n-1, k, max min k inv n 1 Æ min·max Æ root!=null • Another lemma: x: : sortl n, min, max ) x: : lseg n, null Lemma is required for bubble sorting. 9
 Yet Another Lemma • Two predicates from same data structure. dll n, p root=null n=0 root node 2 _, p, r r: : dll n-1, root inv n 0 tree n root=null n=0 root node 2 , lt, rt lt: : tree a rt: : tree b Æ n=1+a+b inv n 0 • Corner cases are related: n · 1 ) (x: : tree
Yet Another Lemma • Two predicates from same data structure. dll n, p root=null n=0 root node 2 _, p, r r: : dll n-1, root inv n 0 tree n root=null n=0 root node 2 , lt, rt lt: : tree a rt: : tree b Æ n=1+a+b inv n 0 • Corner cases are related: n · 1 ) (x: : tree
 Outline • • Motivation Background Entailment Lemmas Soundness Experiments Conclusion 11
Outline • • Motivation Background Entailment Lemmas Soundness Experiments Conclusion 11
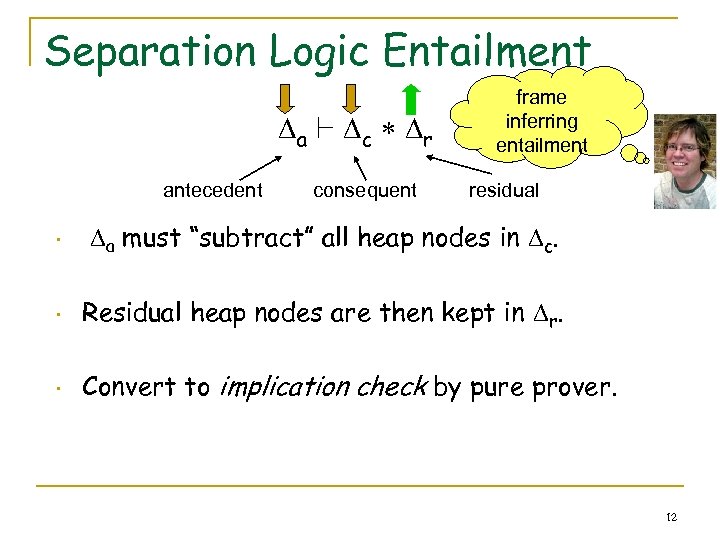 Separation Logic Entailment a ` c r antecedent consequent frame inferring entailment residual • a must “subtract” all heap nodes in c. • Residual heap nodes are then kept in r. • Convert to implication check by pure prover. 12
Separation Logic Entailment a ` c r antecedent consequent frame inferring entailment residual • a must “subtract” all heap nodes in c. • Residual heap nodes are then kept in r. • Convert to implication check by pure prover. 12
 Entailment Algorithm (VMCAI 07) 13
Entailment Algorithm (VMCAI 07) 13
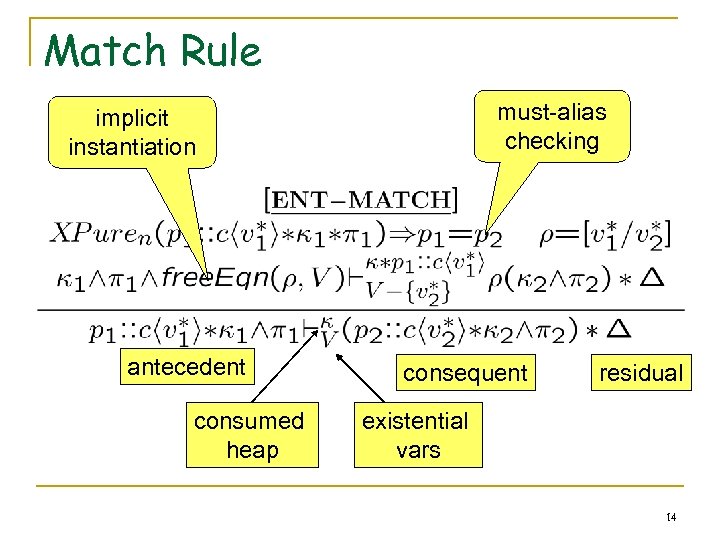 Match Rule must-alias checking implicit instantiation antecedent consumed heap consequent residual existential vars 14
Match Rule must-alias checking implicit instantiation antecedent consumed heap consequent residual existential vars 14
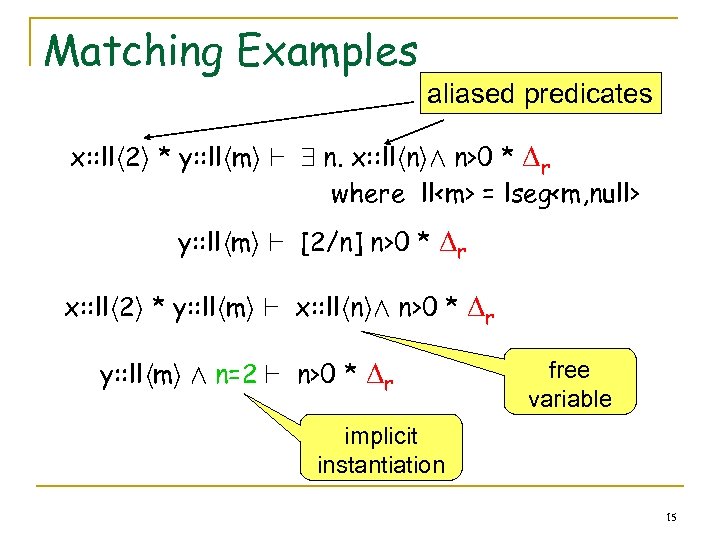 Matching Examples aliased predicates x: : llh 2 i * y: : llhmi ` 9 n. x: : llhniÆ n>0 * r where ll
Matching Examples aliased predicates x: : llh 2 i * y: : llhmi ` 9 n. x: : llhniÆ n>0 * r where ll
 Source of Free Variables Specification void insert(node x, int v) requires x: : llhni Æ n>0 ensures x: : llhn+1 i free variable linking pre and post conditions 16
Source of Free Variables Specification void insert(node x, int v) requires x: : llhni Æ n>0 ensures x: : llhn+1 i free variable linking pre and post conditions 16
 Empty Rule • Entailment is reduced to implication of pure constraints when the consequent’s heap is empty heap 17
Empty Rule • Entailment is reduced to implication of pure constraints when the consequent’s heap is empty heap 17
 Approximation: Examples • XPuren(x nodeh i y nodeh i) = (ex i. x=i Æ i>0) (ex j. y=j Æ j>0) = i, j. (x=i Æ i>0 Æ y=j Æ j>0 Æ i j) = x>0 Æ y>0 Æ x y • XPure 0(x: : llhmi) • XPure 1(x: : llhmi) =m¸ 0 = x=0 Æ m=0 Ç x>0 Æ m-1¸ 0 too weak more info 18
Approximation: Examples • XPuren(x nodeh i y nodeh i) = (ex i. x=i Æ i>0) (ex j. y=j Æ j>0) = i, j. (x=i Æ i>0 Æ y=j Æ j>0 Æ i j) = x>0 Æ y>0 Æ x y • XPure 0(x: : llhmi) • XPure 1(x: : llhmi) =m¸ 0 = x=0 Æ m=0 Ç x>0 Æ m-1¸ 0 too weak more info 18
 Entailment Proof Trace r y: : llhmi Æ n=2 Æ XPure 1(x: : ll<2>) y: : llhmi Æ n=2 Æ x>0 XPure(y: : llhmi*x: : ll<2>)Æ n=2 ) n>0 y: : llhmi Æ n=2 ` n>0 x: : llh 2 i * y: : llhmi ` x: : llhniÆ n>0 empty step matching step 19
Entailment Proof Trace r y: : llhmi Æ n=2 Æ XPure 1(x: : ll<2>) y: : llhmi Æ n=2 Æ x>0 XPure(y: : llhmi*x: : ll<2>)Æ n=2 ) n>0 y: : llhmi Æ n=2 ` n>0 x: : llh 2 i * y: : llhmi ` x: : llhniÆ n>0 empty step matching step 19
 Outline • • Motivation Background Entailment Lemmas • • • Simple Lemmas Complex Lemma Soundness Experiments Conclusion 20
Outline • • Motivation Background Entailment Lemmas • • • Simple Lemmas Complex Lemma Soundness Experiments Conclusion 20
 Lemmas with Simple LHS Weakening x: : c 1 v 1* ) 9 v* ¢ x: : c 2 v 2* Æ Strengthening simple LHS x: : c 1 v 1* ( 9 v* ¢ x: : c 2 v 2* Æ Equivalence free( ) µ {x, v*1} x: : c 1 v 1* , 9 v* ¢ x: : c 2 v 2* Æ Use unfold/fold techniques 21
Lemmas with Simple LHS Weakening x: : c 1 v 1* ) 9 v* ¢ x: : c 2 v 2* Æ Strengthening simple LHS x: : c 1 v 1* ( 9 v* ¢ x: : c 2 v 2* Æ Equivalence free( ) µ {x, v*1} x: : c 1 v 1* , 9 v* ¢ x: : c 2 v 2* Æ Use unfold/fold techniques 21
 Unfolding a Lemma • A lemma • is ) or , • is an alternative way to unfold a predicate. • is applied if we can find a substitution that matches H to p 1: : c 1
Unfolding a Lemma • A lemma • is ) or , • is an alternative way to unfold a predicate. • is applied if we can find a substitution that matches H to p 1: : c 1
 Folding a Lemma • A lemma fold a predicate with provides an alternative way to ( or , 23
Folding a Lemma • A lemma fold a predicate with provides an alternative way to ( or , 23
 Complex Lemmas Simple Lemma: x: : c 1 v 1* ) 9 v* ¢ x: : c 2 v 2* Æ Complex Lemma: 8 v*. x: : c 1 v 1* 1 1 ) 9 v* ¢ x: : c 2 v 2* 2Æ 2 universally quantified variables complex LHS with more heap {v*} Å ({x, v 1*} [ free( 1)) = {} 24
Complex Lemmas Simple Lemma: x: : c 1 v 1* ) 9 v* ¢ x: : c 2 v 2* Æ Complex Lemma: 8 v*. x: : c 1 v 1* 1 1 ) 9 v* ¢ x: : c 2 v 2* 2Æ 2 universally quantified variables complex LHS with more heap {v*} Å ({x, v 1*} [ free( 1)) = {} 24
 An Example : Complex Lemma Earlier Split Lemma that is simple: x: : lseg n, p ) 9 i, j, r. x: : lseg i, r r: : lseg j, p Æ n=i+j Complex Lemma (with Universally Quantified Vars). 8 i, j. x: : lseg n, p Æ i, j ¸ 0 Æ n=i+j ) 9 r. x: : lseg i, r r: : lseg j, p 25
An Example : Complex Lemma Earlier Split Lemma that is simple: x: : lseg n, p ) 9 i, j, r. x: : lseg i, r r: : lseg j, p Æ n=i+j Complex Lemma (with Universally Quantified Vars). 8 i, j. x: : lseg n, p Æ i, j ¸ 0 Æ n=i+j ) 9 r. x: : lseg i, r r: : lseg j, p 25
 Why Complex Lemma? • Examples handled by Simple Lemma : x: : lseg
Why Complex Lemma? • Examples handled by Simple Lemma : x: : lseg
 List Segment with Bag lseg. B S, p root=p S={} Ç root node a, r r: : lseg. B S 2, p Æ S={a}[S 2 inv true Possible Lemmas? x: : lseg. B S, p , 9 S 1, S 2, r. x: : lseg. B S 1, r r: : lseg. B S 2, p Æ S=S 1 [ S 2 8 S 1, S 2. x: : lseg. B S, p Æ S=S 1 [ S 2 ) 9 r. x: : lseg. B S 1, r r: : lseg. B S 2, p 27
List Segment with Bag lseg. B S, p root=p S={} Ç root node a, r r: : lseg. B S 2, p Æ S={a}[S 2 inv true Possible Lemmas? x: : lseg. B S, p , 9 S 1, S 2, r. x: : lseg. B S 1, r r: : lseg. B S 2, p Æ S=S 1 [ S 2 8 S 1, S 2. x: : lseg. B S, p Æ S=S 1 [ S 2 ) 9 r. x: : lseg. B S 1, r r: : lseg. B S 2, p 27
 Unfolding Complex Lemma • Complex lemma with universal vars and extra E 8 v* ¢ (H * EÆ G ) B) extra heap term to remove variables to be instantiated 28
Unfolding Complex Lemma • Complex lemma with universal vars and extra E 8 v* ¢ (H * EÆ G ) B) extra heap term to remove variables to be instantiated 28
 An Entailment Proof Trace r n=8 Æ a, b ¸ 0 Æ n=a+b Æ a=2 Æ b=6 n=8 ` 9 a, b ¸ 0 Æ n=a+b Æ a=2 Æ b=6 ([i->a, j->b]` i, j¸ 0 Æ n=i+j) Æ n=8 ` a=2 Æ b=6 q: : lseg
An Entailment Proof Trace r n=8 Æ a, b ¸ 0 Æ n=a+b Æ a=2 Æ b=6 n=8 ` 9 a, b ¸ 0 Æ n=a+b Æ a=2 Æ b=6 ([i->a, j->b]` i, j¸ 0 Æ n=i+j) Æ n=8 ` a=2 Æ b=6 q: : lseg
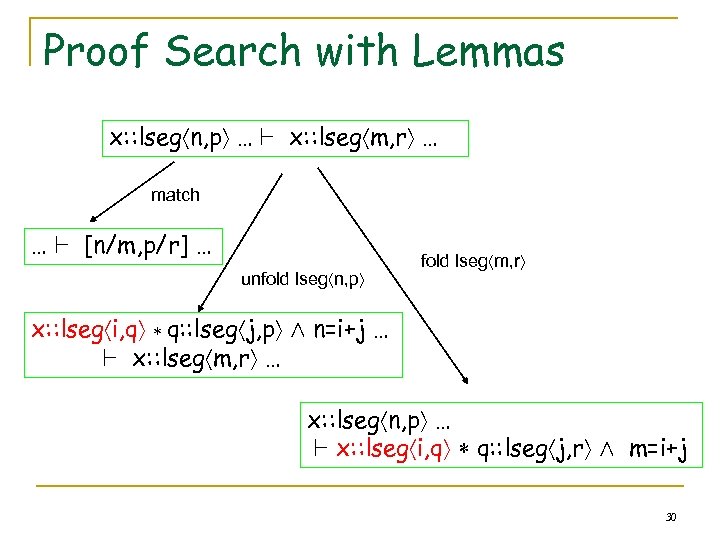 Proof Search with Lemmas x: : lseg n, p … ` x: : lseg m, r … match … ` [n/m, p/r] … unfold lseg n, p fold lseg m, r x: : lseg i, q q: : lseg j, p Æ n=i+j … ` x: : lseg m, r … x: : lseg n, p … ` x: : lseg i, q q: : lseg j, r Æ m=i+j 30
Proof Search with Lemmas x: : lseg n, p … ` x: : lseg m, r … match … ` [n/m, p/r] … unfold lseg n, p fold lseg m, r x: : lseg i, q q: : lseg j, p Æ n=i+j … ` x: : lseg m, r … x: : lseg n, p … ` x: : lseg i, q q: : lseg j, r Æ m=i+j 30
 Outline • • Motivation Background Entailment Lemmas Soundness Experiments Conclusion 31
Outline • • Motivation Background Entailment Lemmas Soundness Experiments Conclusion 31
![Correctness • • • Lemmas proving via cyclic proofs [Brotherston SAS 07]. Soundness from Correctness • • • Lemmas proving via cyclic proofs [Brotherston SAS 07]. Soundness from](https://present5.com/presentation/2a98ca530cd8d3ea0c7ea26544cc85e6/image-32.jpg) Correctness • • • Lemmas proving via cyclic proofs [Brotherston SAS 07]. Soundness from cyclic proof + antecedent weakening + consequent strengthening. Terminating with well-founded predicates and lemmas and goal-directed rewriting. 32
Correctness • • • Lemmas proving via cyclic proofs [Brotherston SAS 07]. Soundness from cyclic proof + antecedent weakening + consequent strengthening. Terminating with well-founded predicates and lemmas and goal-directed rewriting. 32
 Outline • • Motivation Background Entailment Lemmas Soundness Experiments Conclusion 33
Outline • • Motivation Background Entailment Lemmas Soundness Experiments Conclusion 33
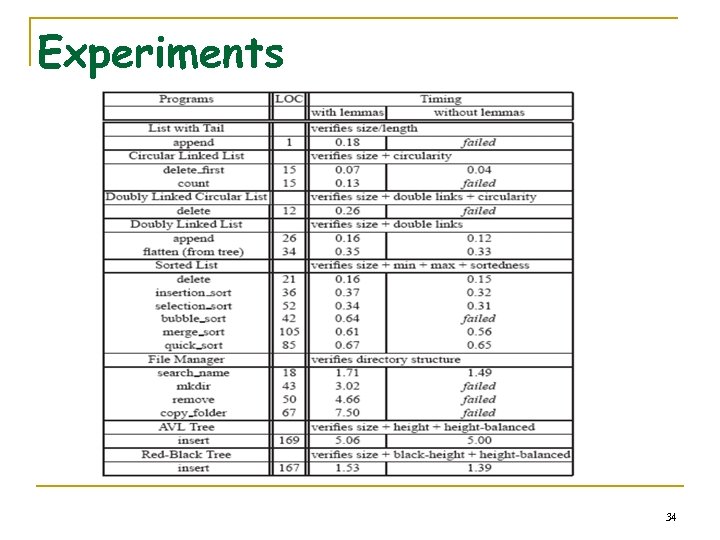 Experiments 34
Experiments 34
 Conclusion • • • Automatically prove and apply user-defined lemma in separation logic. Terminating and directed lemma applications. Lemmas important for more verifications • • with arrays and pointer arithmetic. with OO extension + abstract predicates. 35
Conclusion • • • Automatically prove and apply user-defined lemma in separation logic. Terminating and directed lemma applications. Lemmas important for more verifications • • with arrays and pointer arithmetic. with OO extension + abstract predicates. 35
 Thank You! 36
Thank You! 36
 Lemma Proving • • Lemmas proved via the entailment. During entailment proving, the lemma itself can be used as an instance of cyclic proof. Obligation for proving ) and , lemmas: unfold (H * E Æ G, root) ` B * emp Obligation for proving ( and , lemmas: unfold (B, root) ` (H * E Æ G) * emp 37
Lemma Proving • • Lemmas proved via the entailment. During entailment proving, the lemma itself can be used as an instance of cyclic proof. Obligation for proving ) and , lemmas: unfold (H * E Æ G, root) ` B * emp Obligation for proving ( and , lemmas: unfold (B, root) ` (H * E Æ G) * emp 37
 Specification Language 38
Specification Language 38
 Translating to Pure Form 39
Translating to Pure Form 39
 Equivalent Complex Lemma 8 i, j ¸ 0 Æ n=i+j ) x: : lseg
Equivalent Complex Lemma 8 i, j ¸ 0 Æ n=i+j ) x: : lseg
 An Example class node {int val; node next} class node 2 {int val; node 2 prev; node 2 next} root: : ll
An Example class node {int val; node next} class node 2 {int val; node 2 prev; node 2 next} root: : ll == root=null Æ s=0 Ç 9 r ¢ root: : node<_, r>*r: : ll == root=null Æ s=0 Ç 9 r 1, r 2 ¢ root: : node 2<_, r 1, r 2>*r 2: : dseg. N
 Delete Operation 42
Delete Operation 42
 List with Tail Pointer root n tx List with Tail Pointer root: : lltail tx, n root node a, r Æ n=1 Æ root=tx Ç root node a, r r: : lltail tx, n-1 inv n¸ 1 void append(node x, node tx, node y, node ty) { // x: : lltail tx, n * y: ; lltail
List with Tail Pointer root n tx List with Tail Pointer root: : lltail tx, n root node a, r Æ n=1 Æ root=tx Ç root node a, r r: : lltail tx, n-1 inv n¸ 1 void append(node x, node tx, node y, node ty) { // x: : lltail tx, n * y: ; lltail
 List with Tail Pointer Useful Lemmas root: : lltail tx, n , root: : lseg
List with Tail Pointer Useful Lemmas root: : lltail tx, n , root: : lseg
 Specification Language 45
Specification Language 45
 Approximation • • Entailment is reduced to implication of pure constraints when the consequent’s heap is empty. Each predicate is approximated by a pure constraint. 46
Approximation • • Entailment is reduced to implication of pure constraints when the consequent’s heap is empty. Each predicate is approximated by a pure constraint. 46
 Two Examples Fail to find proof : x=null ` x: : llhniÆ n>0 * r where x: : ll
Two Examples Fail to find proof : x=null ` x: : llhniÆ n>0 * r where x: : ll
 Instantiation Justified x: : llh 2 i * y: : llhmi ` x: : llhniÆ n>0 * r x: : llh 2 i * y: : llhmi ` 9 n. x: : llhniÆ n>0 * r 9 n. x: : llhniÆ n>0 * y: : llhmi 9 n. x: : llhni Æ n>0 * y: : llhmiÆn=2 Æ x>0 : r y: : llhmi Æ n=2 Æ x>0 48
Instantiation Justified x: : llh 2 i * y: : llhmi ` x: : llhniÆ n>0 * r x: : llh 2 i * y: : llhmi ` 9 n. x: : llhniÆ n>0 * r 9 n. x: : llhniÆ n>0 * y: : llhmi 9 n. x: : llhni Æ n>0 * y: : llhmiÆn=2 Æ x>0 : r y: : llhmi Æ n=2 Æ x>0 48
 Example Predicates Singly-linked list root null root: : ll n root=null n=0 9 r. root node a, r r: : ll n 1 derived attribute (c. f. model field) inv n 0 user-supplied invariant Non-empty sorted list sortl n, mi, mx root: : node mi, null mi=mx Æ n=1 root node mi, q q: : sortl n-1, k, mx mi k inv n 1 Æ mi·mx 49
Example Predicates Singly-linked list root null root: : ll n root=null n=0 9 r. root node a, r r: : ll n 1 derived attribute (c. f. model field) inv n 0 user-supplied invariant Non-empty sorted list sortl n, mi, mx root: : node mi, null mi=mx Æ n=1 root node mi, q q: : sortl n-1, k, mx mi k inv n 1 Æ mi·mx 49
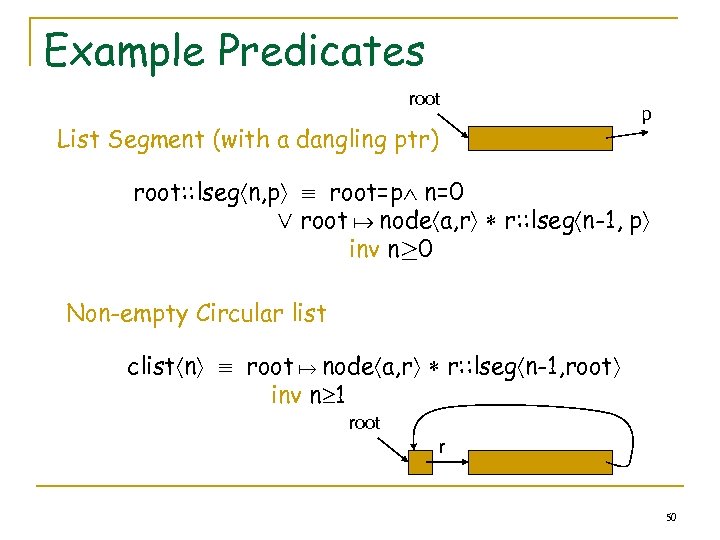 Example Predicates root List Segment (with a dangling ptr) p root: : lseg n, p root=p n=0 Ç root node a, r r: : lseg n-1, p inv n¸ 0 Non-empty Circular list clist n root node a, r r: : lseg n-1, root inv n 1 root r 50
Example Predicates root List Segment (with a dangling ptr) p root: : lseg n, p root=p n=0 Ç root node a, r r: : lseg n-1, p inv n¸ 0 Non-empty Circular list clist n root node a, r r: : lseg n-1, root inv n 1 root r 50
 Example Predicates AVL-Tree (near-balanced tree) avl h root = null Æ h = 0 Ç root nodeh, h, p, qi p: : avlhh 1 i q: : avlhh 2 i Æ -1 · h 1 -h 2 · 1 Æ h=1+max(h 1, h 2) inv h¸ 0 51
Example Predicates AVL-Tree (near-balanced tree) avl h root = null Æ h = 0 Ç root nodeh, h, p, qi p: : avlhh 1 i q: : avlhh 2 i Æ -1 · h 1 -h 2 · 1 Æ h=1+max(h 1, h 2) inv h¸ 0 51
 Proof Search (Set of States) 1 ` 2 { 3, . . , n} • • • { 3, . . , n} denotes non-deterministic outcome from proof search. { } means entailment has failed. Modified Floyd-Hoare style forward reasoning : { } code { 1, . . , n} 52
Proof Search (Set of States) 1 ` 2 { 3, . . , n} • • • { 3, . . , n} denotes non-deterministic outcome from proof search. { } means entailment has failed. Modified Floyd-Hoare style forward reasoning : { } code { 1, . . , n} 52
 Equivalence Lemma Definition of list segment is inadequate lseg n, p root=p n=0 root: : node _, r r: : lseg n-1, p inv n 0 basic definition Important to have equivalence coercion : lseg n, p , 9 i, j, r. root: : lseg i, r r: : lseg j, p Æ n=i+j Termination ensured by well-formed and well-founded property extra property 53
Equivalence Lemma Definition of list segment is inadequate lseg n, p root=p n=0 root: : node _, r r: : lseg n-1, p inv n 0 basic definition Important to have equivalence coercion : lseg n, p , 9 i, j, r. root: : lseg i, r r: : lseg j, p Æ n=i+j Termination ensured by well-formed and well-founded property extra property 53


