1f63ea7cf43b3c960b7440919b0afb60.ppt
- Количество слайдов: 130
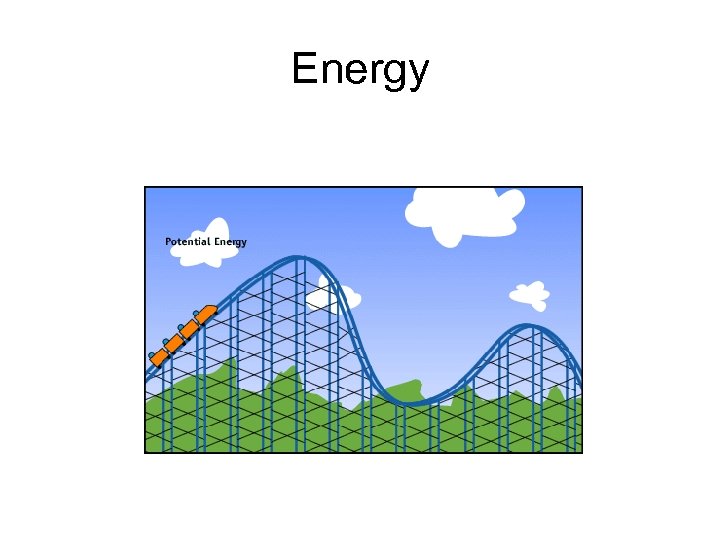
Energy

Energy • Energy – the ability to do work or produce heat • Energy exists in two different forms – kinetic energy & potential energy

Potential Energy • Potential energy – energy due to composition or position of an object • Potential energy is stored energy that results from the attractions or repulsions of other objects

Kinetic Energy • Kinetic energy – the energy of motion • Kinetic energy depends on as objects mass & its velocity • Atoms has mass & they are in motion; therefore they will have kinetic energy
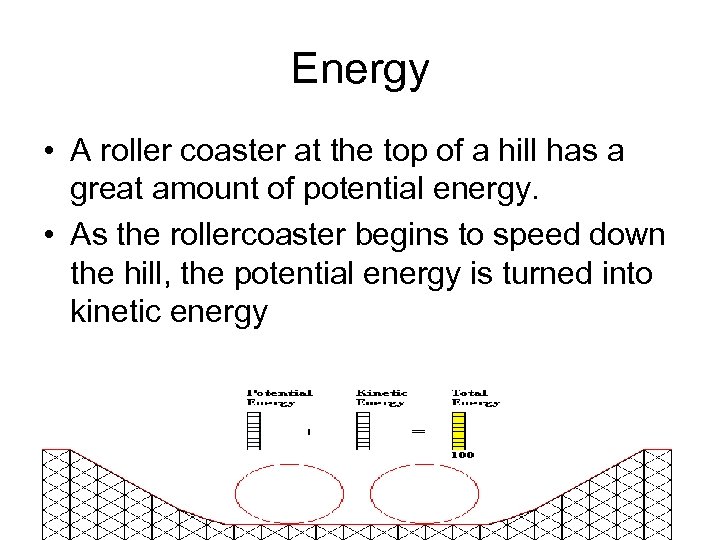
Energy • A roller coaster at the top of a hill has a great amount of potential energy. • As the rollercoaster begins to speed down the hill, the potential energy is turned into kinetic energy

Energy • The SI unit for energy is the joule (J) • 1 J = 1 Kgm 2 / s 2 • Another unit of energy that you may be more familiar with is the calorie • calorie – amount of energy required to raise 1 g of water 1°C • 1 cal = 4. 18 J

Energy • The calories that you eat are actually kilocalories or Calories (with a big C) • 1000 calories = 1 Kilocalorie = 1 Calorie

Energy Conversions • Convert 15, 500 joules into Calories • 15500 J x 1 cal x 1 Cal = • 4. 18 J 1000 cal • 3. 71 Cal

Formulas – Kinetic Energy • • • Kinetic energy KE = ½ mv 2 KE = kinetic energy (joules) m = mass (must be in Kg) V = velocity (must be in m/s)

Formulas – Potential Energy • • • Potential Energy PE = mgh PE = Potential Energy (J) m = mass (Kg) g = gravitational constant = 9. 8 m/s 2 h = height (m)

Formulas - Work • Work (w) – the energy used to move an object against a force • Force (f) – a push or pull on an object • W = mgd = fd = PE • Work and potential energy can be looked at in the same light

Work • It is important to understand that if there is no movement, there is no work done • If I push and push on the demonstration table with all of my might. I may get hot and sweaty and feel like I have done a TON of work, but in reality I have done NO work because the table has not moved

Examples • A bowler lifts a 5. 4 kg bowling ball 1. 6 m and then drops it to the ground. • How much work was required to raise the ball? • W = mgd • W = (5. 4 kg)(9. 8 m/s 2)(1. 6 m) • 85 Kgm 2/s 2 = 85 J

Examples • How much potential energy does that ball have at this height? • 85 J

Examples • If the mass is dropped and we assume that all of the potential energy is turned into kinetic energy, at what velocity will the bowling ball hit the ground? • KE = PE = 85 J • m = 5. 4 Kg • V=?

Examples • • KE = ½ mv 2 85 J = ½ (5. 4 Kg) v 2 = 31. 5 v = 5. 6 m/s

More examples • What is the kinetic energy of 1 atom of Ar moving at 650 m/s? • KE = ½ mv 2 • 1 atom Ar x 1 mol Ar x 39. 95 g Ar x 1 Kg Ar = • 6. 02 x 1023 atoms 1 mol Ar 1 x 103 g Ar • 6. 64 x 10 -26 kg Ar
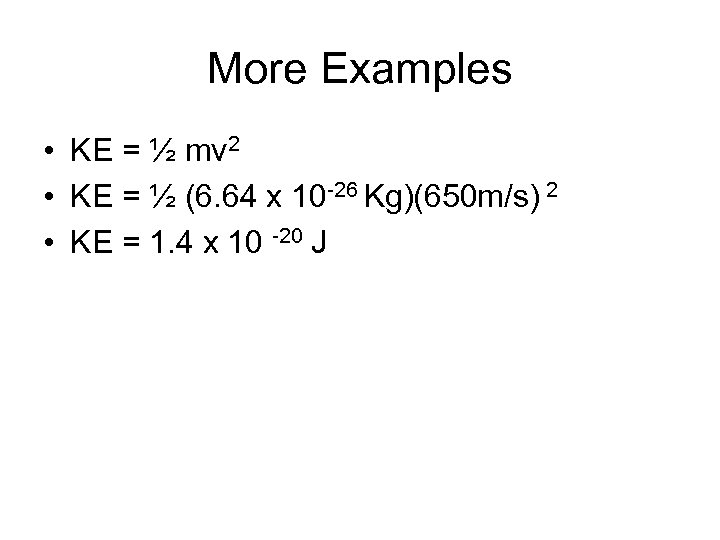
More Examples • KE = ½ mv 2 • KE = ½ (6. 64 x 10 -26 Kg)(650 m/s) 2 • KE = 1. 4 x 10 -20 J

1 st Law of Thermodynamics • 1 st Law of Thermodynamics – energy is conserved • The law of conservation of energy states that in any chemical reaction or physical process, energy can be converted from one form to another, but it is neither created nor destroyed.

1 st Law of Thermodynamics • Since energy can neither be gained nor lost, the change in E can be calculated using: • E = Ef – Ei • In a chemical reaction i indicates reactants and f indicated products

E • E has 3 parts: 1. A # indicating the magnitude 2. A sign (+/-) indicating the direction 3. A unit

Thermochemistry • Thermochemistry is the study of heat changes that accompany chemical reactions and phase changes. • In thermochemistry, the system is the specific part of the universe that contains the reaction or process you wish to study.

Thermochemistry • Everything in the universe other than the system is considered the surroundings. • Therefore, the universe is defined as the system plus the surroundings. universe = system + surroundings

Relating E to heat & work • The system can exchange energy with its surroundings in 2 ways: as heat or work • E = q + w • E = change in energy • q = heat • w = work

q&w • Don’t forget q & w must have signs • In order to get the sign you must look at the system as a box and the surroundings as everything else System Surroundings
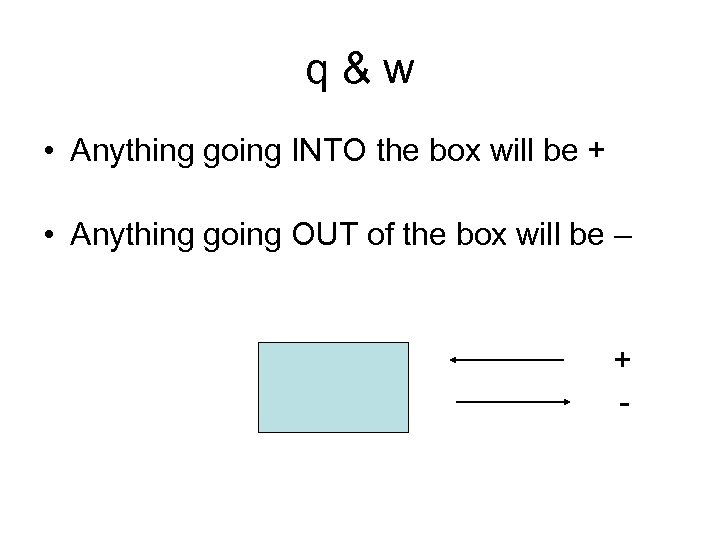
q&w • Anything going INTO the box will be + • Anything going OUT of the box will be – + -
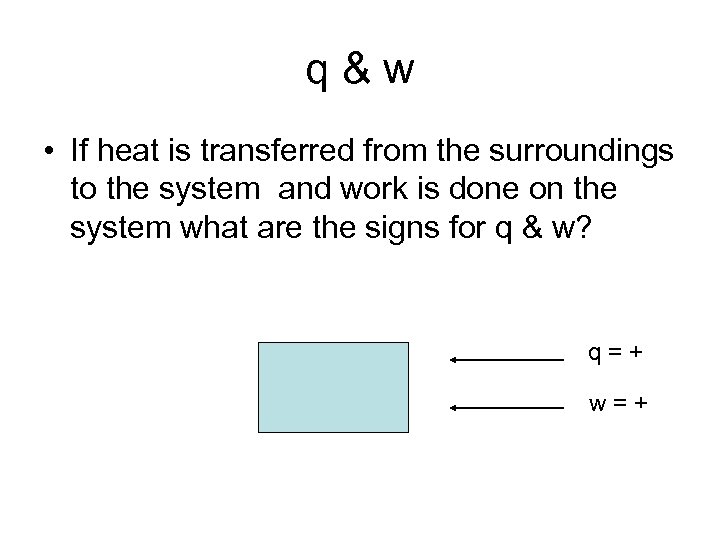
q&w • If heat is transferred from the surroundings to the system and work is done on the system what are the signs for q & w? q=+ w=+
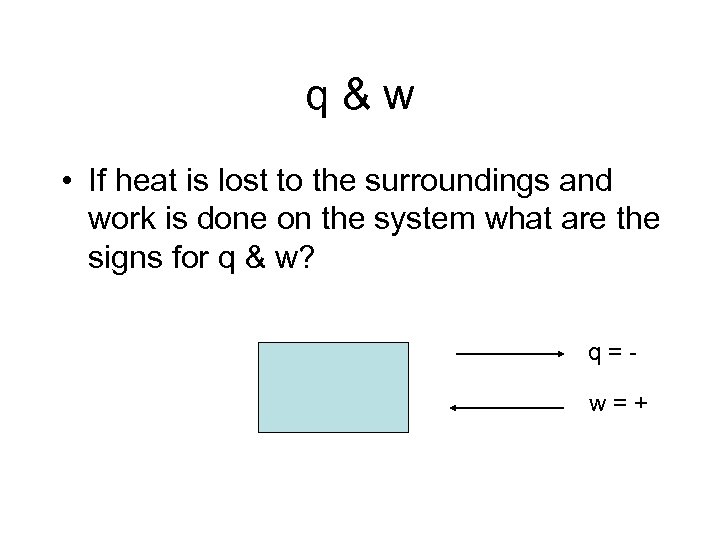
q&w • If heat is lost to the surroundings and work is done on the system what are the signs for q & w? q=w=+

Summary for q & w • • q + = heat into system q - = heat into surroundings w + = work done on the system w - = work done on the surroundings

Examples • A system loses 1150 J of heat to the surroundings and does 480 J of work on the surroundings. Calculate E. • E = q + w • E = (-1150 J) + (-480 J) • E = -1630 J

Examples • A system absorbs 140 J of heat from the surroundings and does 85 J of work on the surroundings. Calculate E. • E = q + w • E = (+ 140 J) + (-85 J) • E = + 55 J

Endothermic & Exothermic • Endothermic – system absorbs heat – Heat flows into the system – Temperature goes down • Exothermic – Heat flows out of the system and into the surroundings – Temperature goes up • Only look at heat (q) to determine if the system is endo or exo

for example, 1. Ice melting at room temperature 2. Dissolving sugar in hot coffee 3. Na(s) + H 2 O(l) Na+(aq) + OH-(aq) + H 2(g)

Entropy

1 st Law of Thermodynamics • Energy is neither created nor destroyed – The energy of the universe is constant – Energy just changes from one form to another • This law lets us know the energy of the system, but does not give us any information about the direction of the energy flow

Spontaneity Spontaneous process – a process that occurs without intervention Spontaneous processes can be fast or slow Spontaneity tells us the direction of the energy flow It tells us NOTHING about the speed of the reaction

For example… • A ball spontaneously rolls down a hill – It does not spontaneously roll up • If iron is exposed to air, it spontaneously rusts – The rust does not spontaneously turn back into air & iron

Entropy • Entropy (S) – the measure of molecular randomness or disorder – Think of entropy as the amount of chaos • The driving force for a spontaneous process is an increase in entropy

Entropy • The natural progression of things is from order to disorder • Or from lower entropy to higher entropy – Think of a deck of cards…when you drop one it goes from order to disorder – Think of your room… it goes from order to disorder • Think if entropy as a probability…not a certainty – Nature spontaneously proceeds toward that states that have the highest probability of existing

2 nd Law of Thermodynamics • 2 nd Law of Thermodynamics – In any spontaneous process there is always an increase in entropy of the universe • Energy is conserved…entropy is NOT conserved! • The entropy of the universe is always increasing – S univ = + = spontaneous – S univ = - = not spontaneous (would be spontaneous in the opposite direction) – S univ = 0 = no tendency to occur (system is at equilibrium) • S univ = S sys + S surr

Temperature & Spontaneity Ssurr = _ H T T must be in Kelvin H is usually given in KJ/mol S will be in KJ/K, but is usually changed to J/K

Example Sb 4 O 6 (s) + 6 C (s) 4 Sb (s) + 6 CO (g) H = 778 k. J Calculate Ssurr for this reaction at 25 C and 1 atm S = - ( H/T) S = - (778 KJ/298 K) S = -2. 61 KJ/K S = -2610 J/K

3 rd Law of Thermodynamics • The entropy of a perfect crystal at 0 K is zero

The Surroundings The Universe The System

Lecture - Entropy

Spontaneous Processes the system spontaneous change - no action from outside the system is necessary
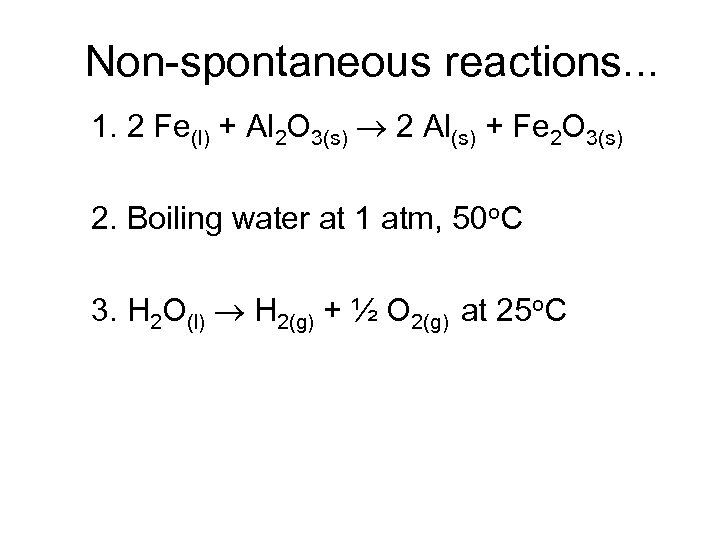
Non-spontaneous reactions. . . 1. 2 Fe(l) + Al 2 O 3(s) 2 Al(s) + Fe 2 O 3(s) 2. Boiling water at 1 atm, 50 o. C 3. H 2 O(l) H 2(g) + ½ O 2(g) at 25 o. C

What about the reverse reactions? 1. Water freezing at room temperature? (ice melts) 2. Sugar precipitating out of hot coffee? (sugar dissolves) 3. Na+(aq) + OH-(aq) + H 2(g) Na(s) + H 2 O(l) ? (reverse reaction occurs)

Entropy • Predict the sign of the entropy change for the following… 1. Sugar is added to water to form a solution + 2. Iodine vapor condenses on a cold surface to produce a liquid -

so why does this reaction work? NH 4 Cl(s) + H 2 O(l) NH 4+(aq) + Cl(aq) Ho = + 15. 1 k. J/mol
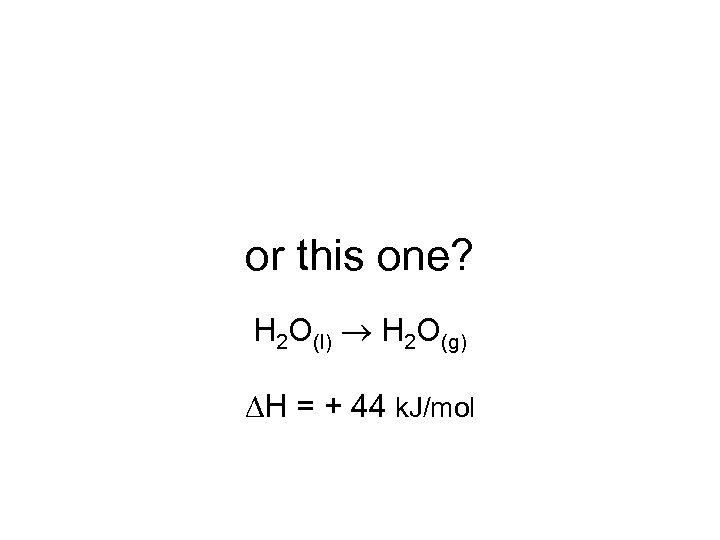
or this one? H 2 O(l) H 2 O(g) H = + 44 k. J/mol
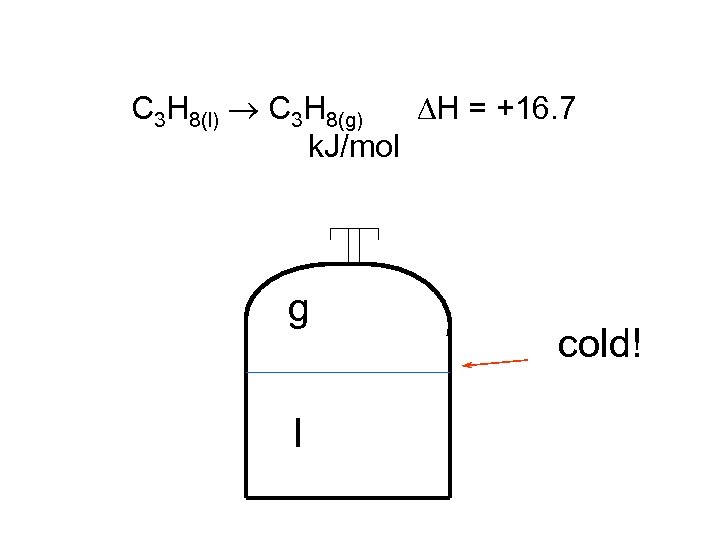
C 3 H 8(l) C 3 H 8(g) H = +16. 7 k. J/mol g l cold!

Heat vs. Energy spontaneous change = heat released? NOT ALWAYS! spontaneous change = energy released? ALWAYS!

Entropy, S - a measure of the disorder of the system

Entropy tends to increase breaking a glass using the library not cleaning up your house

1 st law of thermodynamics: The energy of the universe is constant (The best you can do is break even) 2 nd law of thermodynamics: The entropy of the universe is increasing (You can’t break even)

Low entropy is less probable

according to Boltzmann, S = k ln W k = Boltzmann constant = 1. 38 x 10 -23 J K-1 W = number of ways that state can be achieved

royal flush: 4 hands possible S = 1. 38 x 10 -23 J K-1 ln(4) = 1. 9 x 10 -23 J K-1 pair: 1, 098, 240 hands possible S = 1. 38 x 10 -23 J K-1 ln(1098240) 1. 9 x 10 -22 J K-1

Entropy is a State Function S = Sfinal - Sinitial path taken is irrelevant rate of change is irrelevant

S > 0 for: - melting - vaporizing - making a solution - a reaction that produces an increased number of moles - heating a substance
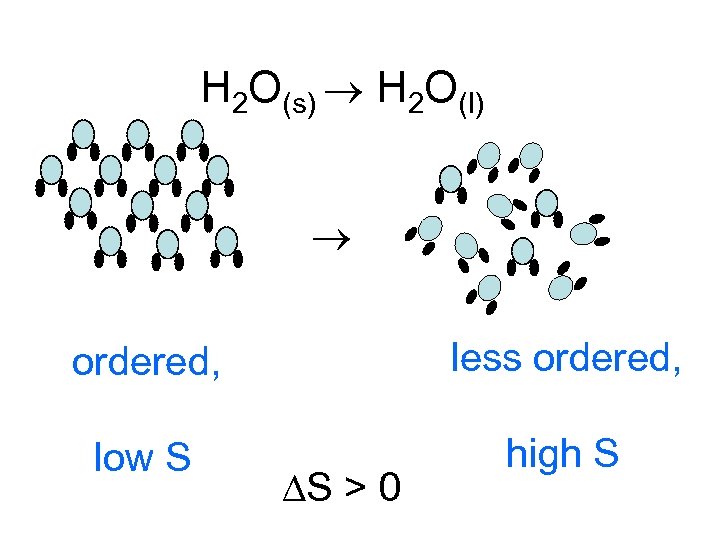
H 2 O(s) H 2 O(l) ordered, less ordered, low S high S S > 0

S > 0 for: - melting - vaporizing - making a solution - a reaction that produces an increased number of moles - heating a substance
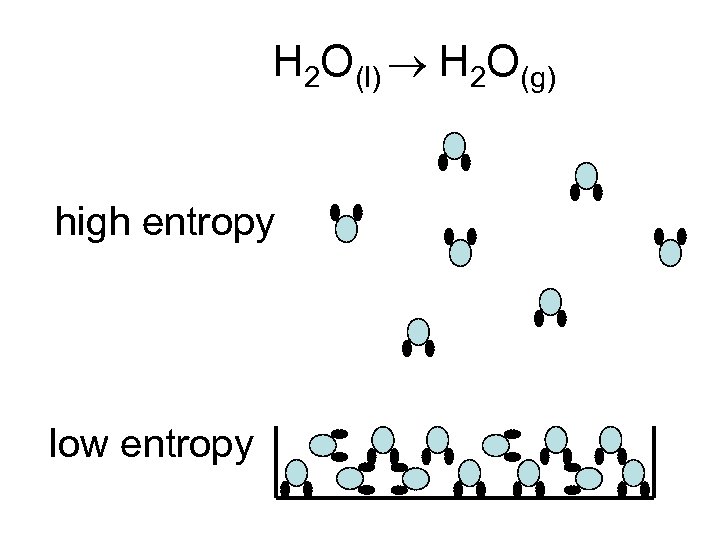
H 2 O(l) H 2 O(g) high entropy low entropy

S > 0 for: - melting - vaporizing - making a solution - a reaction that produces an increased number of moles - heating a substance
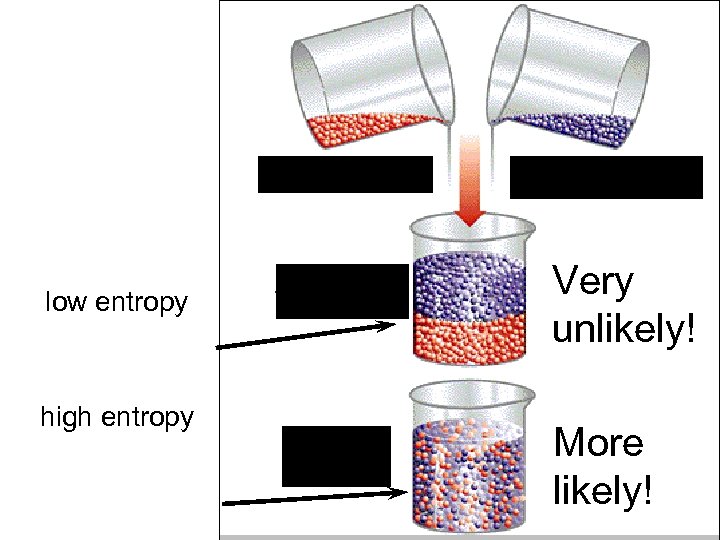
Benzene low entropy high entropy Toluene Very unlikely! More likely!

recall this one? NH 4 Cl(s) + H 2 O(l) NH 4+(aq) + Cl(aq) H>0 (unfavorable) S>0 (favorable!!)

S > 0 for: - melting - vaporizing - making a solution - a reaction that produces an increased number of moles - heating a substance

Ba(OH)2· 8 H 2 O(s) + 2 NH 4 NO 3(s) Ba(NO 3)2(aq) + 2 NH 3(aq) + 10 H 2 O(l) H = +80. 3 k. J (unfavorable) 3 moles 13 moles S > 0 (favorable)

S > 0 for: - melting - vaporizing - making a solution - a reaction that produces an increased number of moles - heating a substance
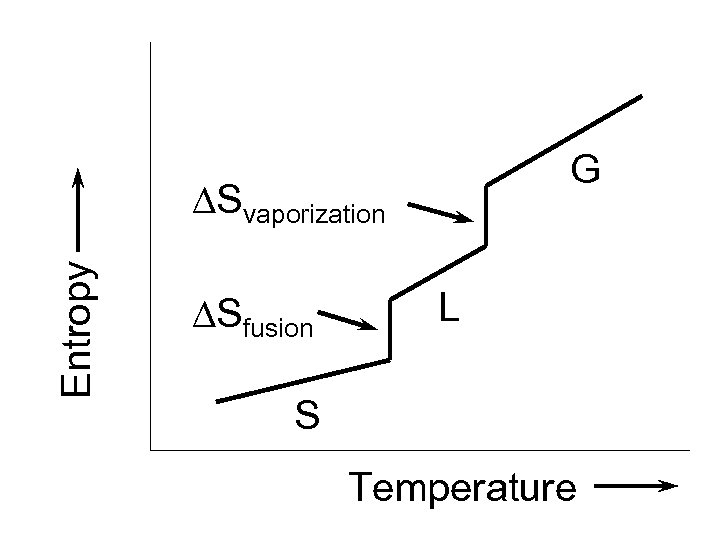
G Entropy Svaporization Sfusion L S Temperature

Calculating S for a reaction Srxn = S(ni Soi) absolute entropy stoichiometric coefficient of species i

for example, C 8 H 18(g) + 12. 5 O 2(g) 8 CO 2(g) + 9 H 2 O(g) 13. 5 moles 17 moles (expect S > 0) Srxn = S(ni Soi)

Entropy • Predict which has the highest entropy 1. CO 2 (s) or CO 2 (g) 2. 1 mol of N 2 at 1 atm or 1 mol of N 2 at 0. 001 atm
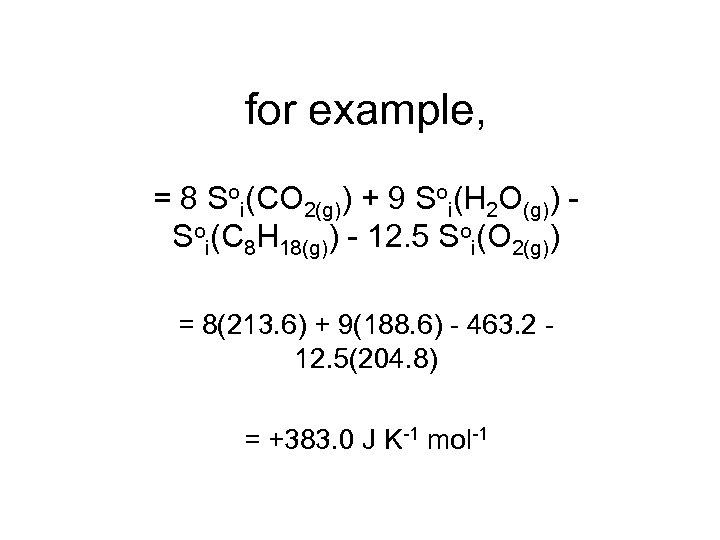
for example, = 8 Soi(CO 2(g)) + 9 Soi(H 2 O(g)) Soi(C 8 H 18(g)) - 12. 5 Soi(O 2(g)) = 8(213. 6) + 9(188. 6) - 463. 2 12. 5(204. 8) = +383. 0 J K-1 mol-1

The Food Calorie 1 kcal = 1000 cal 1 Cal = 1 kcal 1 Cal = 4180 J 2, 000 Cal/day is a meager diet.

what if you drank gasoline?

How much would you need? 1. 2. Assume gasoline is octane (C 8 H 18(l)) Find Hcombustion MW = 114. 2 g/mol r = 0. 70 g/m. L

How much would you need? 1. 2. Assume gasoline is octane (C 8 H 18(l)) Find Hcombustion C 8 H 18(l) + 12. 5 O 2(g) 8 CO 2(g) + 9 H 2 O(g) Hcombustion = 8(-393)+9(-285. 6) - (-208. 2) = -5506. 2 k. J/mol
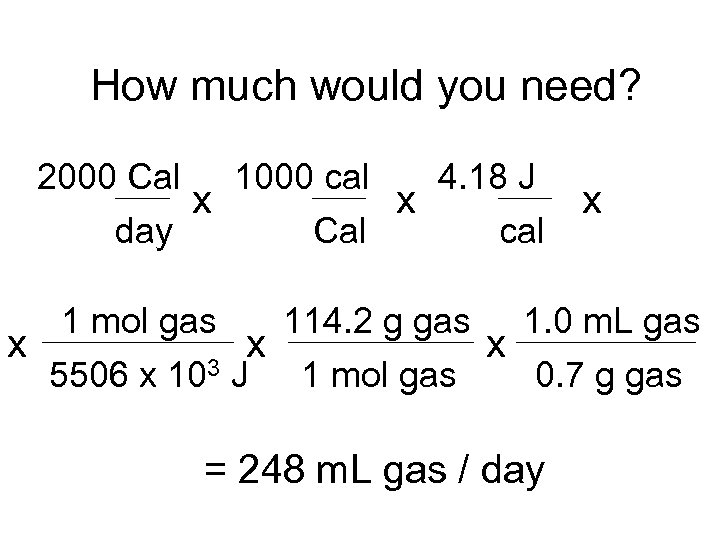
How much would you need? 4. 18 J 2000 Cal 1000 cal x x day Cal cal x 1 mol gas 114. 2 g gas 1. 0 m. L gas x x x 5506 x 103 J 1 mol gas 0. 7 g gas = 248 m. L gas / day
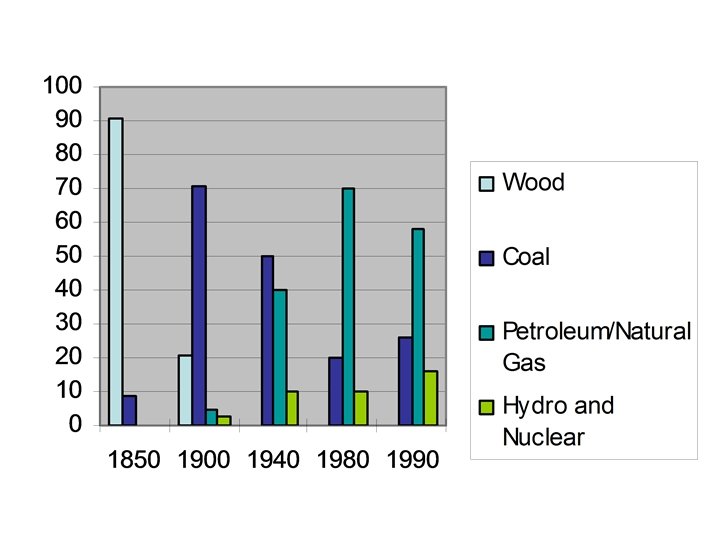
U. S. Energy Usage
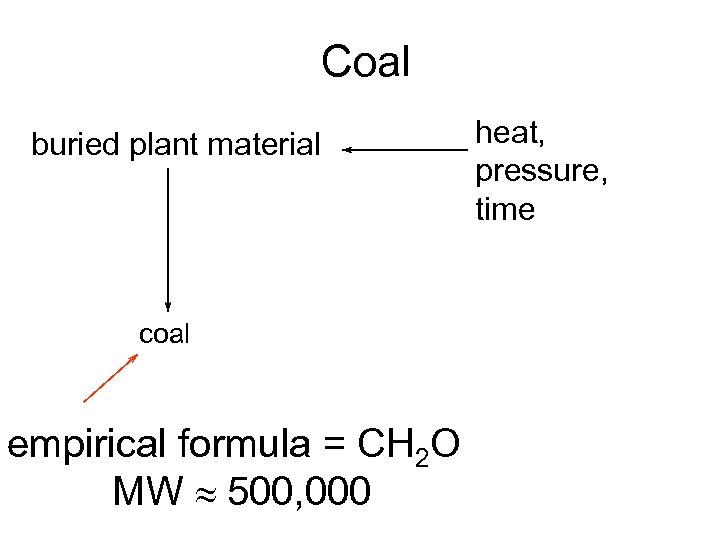
Coal buried plant material coal empirical formula = CH 2 O MW » 500, 000 heat, pressure, time
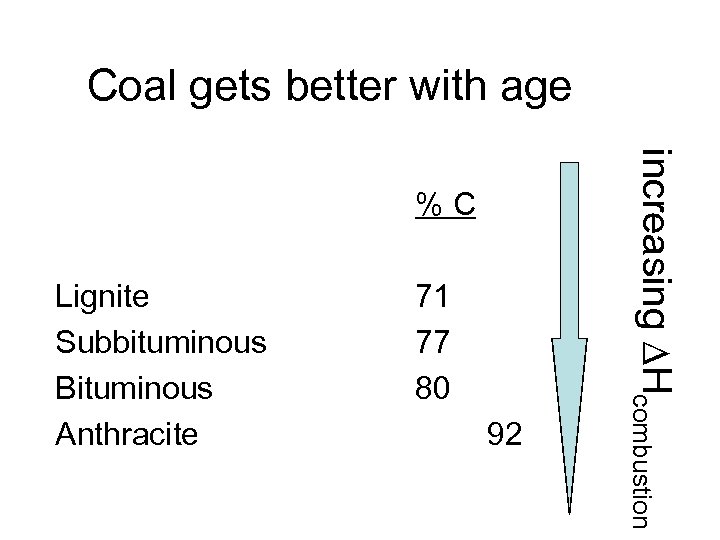
Coal gets better with age Lignite Subbituminous Bituminous Anthracite 71 77 80 92 increasing Hcombustion %C
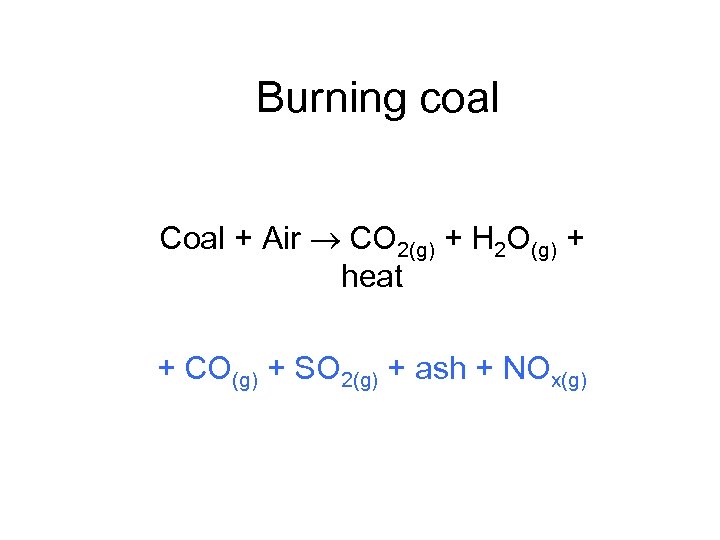
Burning coal Coal + Air CO 2(g) + H 2 O(g) + heat + CO(g) + SO 2(g) + ash + NOx(g)

Other Energy Sources 1. Coal conversion - convert to gaseous fuels - large molecules small molecules - must break C-C bonds - C-H and C-O bonds are made
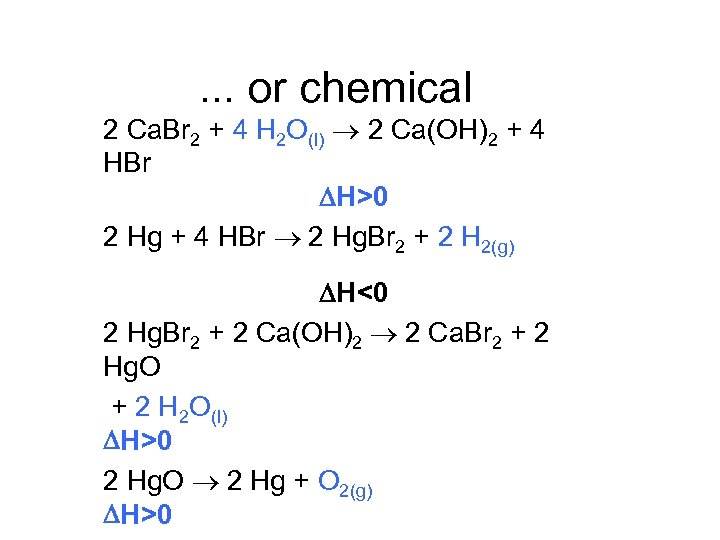
. . . or chemical 2 Ca. Br 2 + 4 H 2 O(l) 2 Ca(OH)2 + 4 HBr H>0 2 Hg + 4 HBr 2 Hg. Br 2 + 2 H 2(g) H<0 2 Hg. Br 2 + 2 Ca(OH)2 2 Ca. Br 2 + 2 Hg. O + 2 H 2 O(l) H>0 2 Hg. O 2 Hg + O 2(g) H>0

Ti(s) + x/2 H 2(g) favored at higher temperature Ti. Hx(s) favored at lower temperature

Free Energy • Free energy (G) – a thermodynamic function equal to the enthalpy minus the product of the entropy and the Kelvin temperature • G = H – T S • A process is only spontaneous in the direction where G is negative

Example • At what temperatures is the following process spontaneous at 1 atm? – Br 2(l) Br 2(g) – H = 31. 0 KJ/mol 31000 J/mol – S = 93. 0 J/ K mol • • G = H – T S 0 = 31000 – T(93. 0) T = 333 K Above 333 K the reaction is spontaneous

Example Sb 2 S 3 (s) + 3 Fe (s) 2 Sb (s) + 3 Fe. S (s) H = -125 k. J Calculate Ssurr for this reaction at 25 C and 1 atm S = - ( H/T) S = - (-125 KJ/298 K) S = 0. 419 KJ/K S = 419 J/K
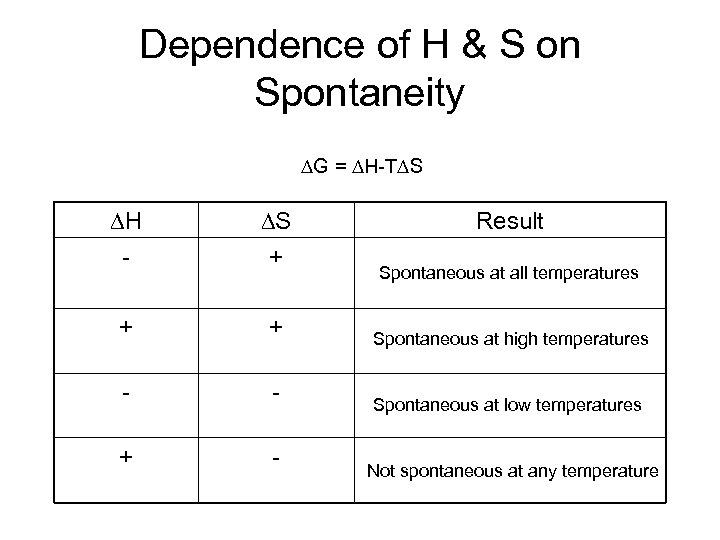
Dependence of H & S on Spontaneity G = H-T S H - S + + + - - + - Result Spontaneous at all temperatures Spontaneous at high temperatures Spontaneous at low temperatures Not spontaneous at any temperature


Hydrocarbons and Heat • Most hydrocarbons are used as fuels. • Knowing how much energy a fuel provides, can tell us if it is useful for a certain application. • For example, the amount of energy a food releases when burned, can tell us about it’s caloric content (fats release lots of energy).
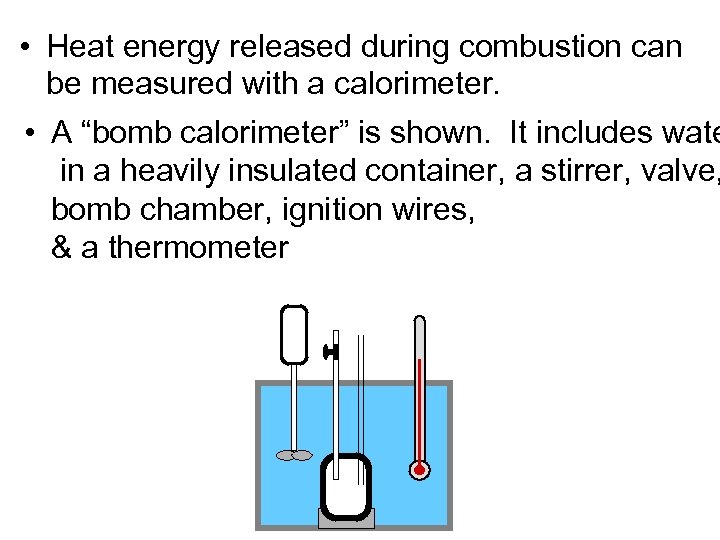
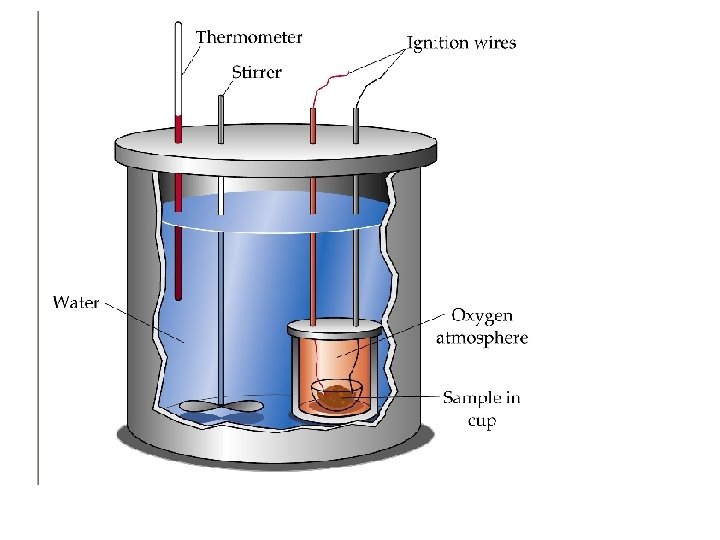
• Heat energy released during combustion can be measured with a calorimeter. • A “bomb calorimeter” is shown. It includes wate in a heavily insulated container, a stirrer, valve, bomb chamber, ignition wires, & a thermometer

Exothermic and Endothermic changes • An alternative to the bomb calorimeter is a “coffee cup” calorimeter, where two nested polystyrene cups take the place of the container • In either case, the change in heat of the water tells us about the reaction of the chemicals.

• An increase in water temperature indicates that the chemicals released energy when they reacted. This is called an “exothermic” reaction. • In an “endothermic” reaction, water temperature decreases as the chemicals absorb energy. • We will see that heat is measured in Joules (J) or kilo. Joules (k. J). Before we do any heat calculations, you should know several terms …

Specific heat capacity The heat needed to the temperature of 1 g of a substance by 1 C. Symbol: c, units: J/(g C). + Heat capacity The heat needed to the temperature of an object by 1 C. Symbol: C (=c x m), units: J/ C

Heat of reaction The heat released during a chemical reaction. Symbol: none, units: J. Specific heat (of reaction) The heat released during a chemical reaction per gram of reactant. Symbol: h, units: J/g.

Molar heat of reaction The heat released during a chemical reaction per mole of reactant. Symbol: H, units: J/mol.

Heat Calculations • To determine the amount of heat a substance produces or absorbs we often use q = cm T • q: heat in J, c: specific heat capacity in J/(g C), m: mass in g, T: temperature change in C, • This equation makes sense if you consider units J x g x C J= g C For a list of c values see page 568 (table 3) Sample problem: (must know water = 4. 18 J/g C) When 12 g of a food was burned in a calorimeter, the 100 m. L of water in the calorimeter changed from 20 C to 33 C. Calculate the heat released. q=cm T = 4. 18 J/(g C) x 100 g x 13 C = 5. 4 k. J

More practice 1. 5 g of copper was heated from 20 C to 80 C. How much energy was used to heat the Cu? q=cm T = 0. 38 J/(g C) x 5 g x 60 C = 114 J 2. If a 3. 1 g ring is heated using 10. 0 J, it’s temp. rises by 17. 9 C. Calculate the specific heat capacity of the ring. Is the ring pure gold? q=cm T 10. 0 J c = q/m T= = 0. 18 J/(g°C) 3. 1 g x 17. 9 C The ring is not pure. Gold is 0. 13 J/(g C) -pg. 568
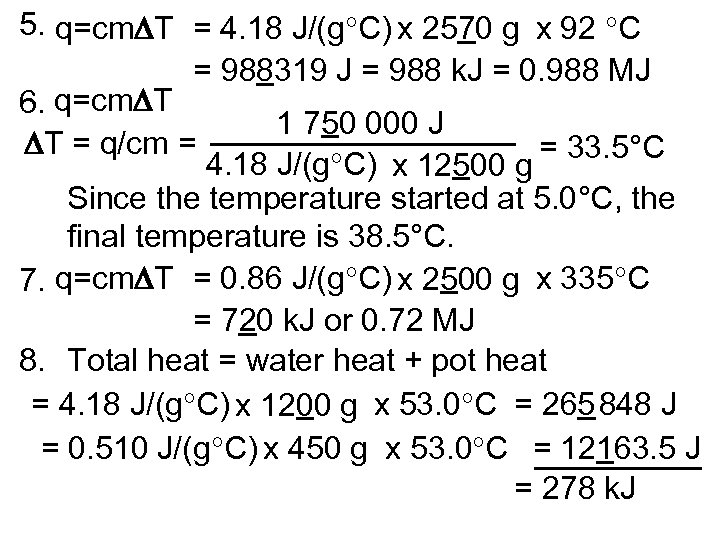
5. q=cm T = 4. 18 J/(g C) x 2570 g x 92 C = 988319 J = 988 k. J = 0. 988 MJ 6. q=cm T 1 750 000 J T = q/cm = = 33. 5°C 4. 18 J/(g C) x 12500 g Since the temperature started at 5. 0°C, the final temperature is 38. 5°C. 7. q=cm T = 0. 86 J/(g C) x 2500 g x 335 C = 720 k. J or 0. 72 MJ 8. Total heat = water heat + pot heat = 4. 18 J/(g C) x 1200 g x 53. 0 C = 265 848 J = 0. 510 J/(g C) x 450 g x 53. 0 C = 12163. 5 J = 278 k. J

How much heat is required to change 50. 0 g of ice at 0 degrees to steam at 100 degrees You are looking for q water at 0 C Ice at 0 C H f mi + water at 100 C mwcw T + Hf for water = 334 j/g = 80 cal (334 j)(50. 0 g) g H vm w Hv = 2257 j = 540 cal + (50. 0 g)(4. 18 j)(100 C) g. C 16700 j + steam at 100 C 20900 j + + (2257 j) ( 50. 0 g) g 112850 j

Heat Capacity Calculations • Recall that heat capacity (J/ C) is different from specific heat capacity (J/g C). • Heat capacity is sometimes a more useful value • For example, because a calorimeter includes wires, the stirrer, thermometer, etc. some heat will be transferred to these other materials. • Rather than having to calculate q for each material a J/ C value is used. Sample problem: q=cm T A calorimeter has a heat capacity of 2. 05 k. J/ C. How much heat is released if the temperature change in the calorimeter is 11. 6 C? q = cm T q= 2. 05 k. J/ C x 11. 6 C = 23. 8 k. J

Thermochemical Equations Thermochemical equations are chemical equations with an added heat term. • KBr. O 3(s) + 42 k. J KBr. O 3(aq) This is endothermic (heat is absorbed/used) • 2 Mg(s) + O 2(g) 2 Mg. O(s) + 1200 k. J This is exothermic (heat is produced/released) Read 12. 3 (pages 582 – 585). Do 2 -6 (pg. 585). Sample problem: 3. 00 g of octane was burned in a calorimeter with excess oxygen, the 1000 m. L of water in the calorimeter rose from 23. 0 C to 57. 6 C. Write thermochemical equation for octane, representing the molar heat of combustion.

2. Specific refers to mass in grams. 3. Specific heat of reaction: J/g or k. J/g, etc. Molar heat of reaction: J/mol or k. J/mol, etc. 4. J/mol = J/g x g/mol (molar mass is used) 5. Exothermic. E. g. CH 4 + 2 O 2 CO 2 + 2 H 2 O + x k. J Other examples include propane, octane, Mg 6. 49. 90 k. J 26. 04 g = 1299 k. J/mol x g mol C 2 H 2 + 2. 5 O 2 2 CO 2 + H 2 O + 1299 k. J or 2 C 2 H 2 + 5 O 2 4 CO 2 + 2 H 2 O + 2598 k. J

Sample: First, calculate the heat released by the combustion reaction via q=cm T … = 4. 18 J/(g C) x 1000 g x 34. 6 C = 144 628 J Octane (C 8 H 18) has a molar mass of 114. 26 g/mol We can determine the molar heat of reaction 1) via the specific heat of reaction or 2) directly h = J = 144 628 J H = 48. 2 k. J x 114. 26 g g 3. 00 g g mol = 48209 J/g = 48. 2 k. J/g = 5508 k. J/mol or J 144 628 J H = = 5508 k. J/mol = mol 0. 0263 mol C 8 H 18 + 12. 5 O 2 8 CO 2 + 9 H 2 O + 5508 k. J For more lessons, visit www. chalkbored. com

Entropy & Chemical Reactions

2 nd Law of Thermodynamics • A process will be spontaneous is the entropy of the universe increases • Now we will look at entropy regarding to chemical reactions

What is the sign for S? • N 2(g) + 3 H 2(g) 2 NH 3(g) • First look at the states…if you go from a solid or a liquid to a gas, you will have a + entropy • In this case, all of the states are the same, so we look at the number of moles • N 2(g) + 3 H 2(g) 2 NH 3(g) • 1 + 3 vs. 2 • The entropy decreases because you go from 4 moles to 2 • S is negative

What is the sign for S? • 4 NH 3 + 5 O 2 4 NO + 6 H 2 O • 9 moles vs. 10 moles • S increases (+)

Calculating S • Calculating S is just like calculating H • Simply use the Appendix…just look at the column for S instead of H • S° of any element or diatomic molecule is NOT zero. • You must look these up!

Example • • Calculate S for the following reaction: 2 Ni. S(s) + 3 O 2(g) 2 SO 2(g) + 2 Ni. O (s) 2(-53) + 3(-205) + 2(248) + 2(38) -149 J/K

Example • • Calculate S for the following reaction: Al 2 O 3(s) + 3 H 2(g) 2 Al(s) + 3 H 2 O(g) (-51) + 3(-131) + 2(28) + 3(189) 179 J/K

Gibbs Free Energy & Chemical Reactions • 1. 2. 3. You can calculate G in 3 ways… Like Hess’s Law Like H° With the equation G = H - T S
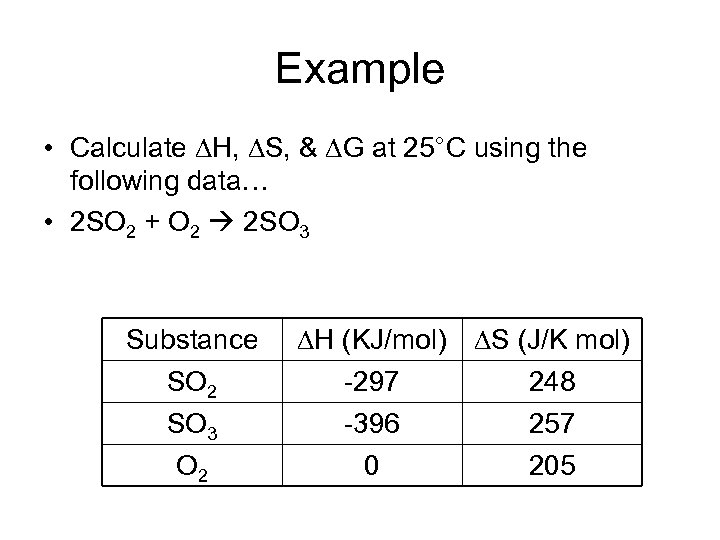
Example • Calculate H, S, & G at 25°C using the following data… • 2 SO 2 + O 2 2 SO 3 Substance SO 2 SO 3 O 2 H (KJ/mol) S (J/K mol) -297 248 -396 257 0 205

Example 2 SO 2 + O 2 2 SO 3 H = 2(+297)+(0) + 2(-396) = -198 KJ S = 2(-248)+ (-205) + 2(257) = -187 J/K G = H – T S =(-198) – (298 x -0. 187) =-142 KJ

Calculate G • Using the following data at 25°C • • Cdiamond + O 2(g) CO 2 (g) G = -397 KJ Cgraphite + O 2(g) CO 2 (g) G = -394 KJ Calculate G for the reaction: C diamond C graphite • G = -3 KJ

Calculating G • Methanol is a high octane fuel used in high performance racing engines. Calculate G for the following reaction • 2 CH 3 OH(g) + 3 O 2(g) 2 CO 2(g) + 4 H 2 O(g) • Given the following free energies of formation: Substance CH 3 OH (g) O 2 (g) CO 2 (g) H 2 O (g) G°(KJ/mol) -163 0 -394 -229

Calculating G • 2 CH 3 OH(g) + 3 O 2(g) 2 CO 2(g) + 4 H 2 O(g) • 2(163) + 3(0) + 2(-394) + 4(-299) • -1378 KJ



Hess’s law • Hess’s Law states that the heat of a whole reaction is equivalent to the sum of it’s steps. • For example: C + O 2 CO 2 The book tells us that this can occur as 2 steps C + ½O 2 CO H = – 110. 5 k. J CO + ½O 2 CO 2 H = – 283. 0 k. J C + CO + O 2 CO + CO 2 H = – 393. 5 k. J I. e. C + O 2 CO 2 H = – 393. 5 k. J • Hess’s law allows us to add equations. • We add all reactants, products, & H values. • We can also show these steps add together via an “enthalpy diagram” …

Steps in drawing enthalpy diagrams 1. Balance the equation(s). 2. Sketch a rough draft based on H values. 3. Draw the overall chemical reaction as an enthalpy diagram (with the reactants on one line, and the products on the other line). 4. Draw a reaction representing the intermediate step by placing the relevant reactants on a line. 5. Check arrows: Start: two leading away Finish: two pointing to finish Intermediate: one to, one away 6. Look at equations to help complete balancing (all levels must have the same # of all atoms). 7. Add axes and H values.
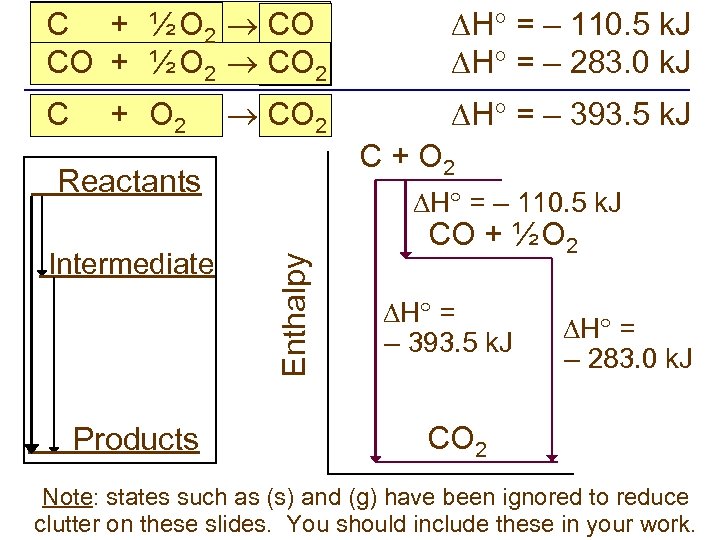
C + ½ O 2 CO CO + ½ O 2 CO 2 H = – 110. 5 k. J H = – 283. 0 k. J CO 2 H = – 393. 5 k. J C + O 2 Reactants Products Enthalpy Intermediate H = – 110. 5 k. J CO + ½ O 2 H = – 393. 5 k. J H = – 283. 0 k. J CO 2 Note: states such as (s) and (g) have been ignored to reduce clutter on these slides. You should include these in your work.

Practice Exercise 6 with Diagram Using example 5. 6 as a model, try PE 6. Draw the related enthalpy diagram. Intermediate H = – 1411. 1 k. J Enthalpy C 2 H 4(g) + 3 O 2(g) 2 CO 2(g) + 2 H 2 O(l) H = – 1411. 1 k. J 2 CO 2(g) + H O(l) C 2 H 5 OH(l) + H = – 44. 0 + 3 H 2 O(l) 3 O 2(g) C 2 H 4(g) 2 H = +1367. 1 C 2 H 5 OH(l) k. J C 2 H 4(g) + + Reactants H = H 2 O(l) Products C 2 H 5 OH(l) 3 O 2(g) + – 44. 0 k. J H = 3 O 2(g) +1367. 1 k. J 2 CO 2(g) +
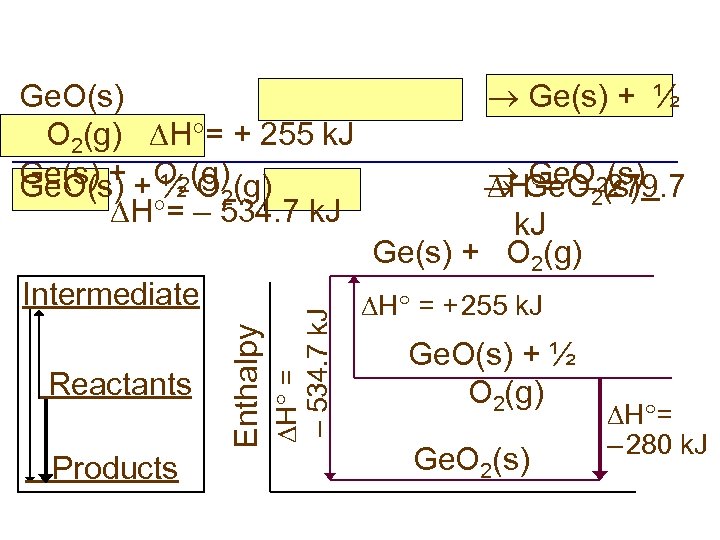
Reactants Products Enthalpy Intermediate H = – 534. 7 k. J Ge. O(s) O 2(g) H = + 255 k. J Ge(s) + + O 2(g) Ge. O(s) ½ O 2 H = – 534. 7 k. J Ge(s) + ½ Ge. O 2(s) Ge. O 279. 7 (s) H = – 2 k. J Ge(s) + O 2(g) H = + 255 k. J Ge. O(s) + ½ O 2(g) Ge. O 2(s) H = – 280 k. J
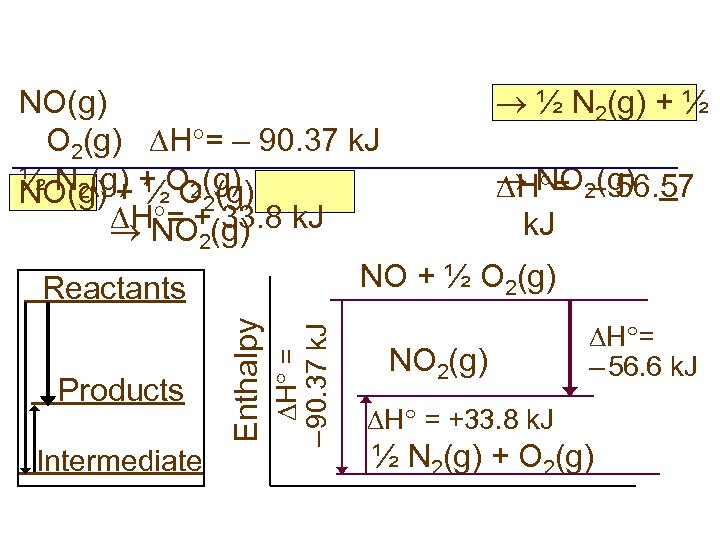
½ N 2(g) + ½ NO(g) O 2(g) H = – 90. 37 k. J ½ N 2(g) ½ O (g) NO(g) + + O 2(g) 2 H = +(g) k. J 33. 8 NO 2(g) H = – 56. 57 k. J 2 NO + ½ O 2(g) Intermediate H = – 90. 37 k. J Products Enthalpy Reactants NO 2(g) H = – 56. 6 k. J H = +33. 8 k. J ½ N 2(g) + O 2(g)

Hess’s law: Example We may need to manipulate equations further: 2 Fe + 1. 5 O 2 Fe 2 O 3 H =? , given Fe 2 O 3 + 3 CO 2 Fe + 3 CO 2 H = – 26. 74 k. J CO + ½ O 2 CO 2 H = – 282. 96 k. J 1: Align equations based on reactants/products. 2: Multiply based on final reaction. 3: Add equations. 2 Fe + 3 CO 2 Fe 2 O 3 + 3 CO H = + 26. 74 k. J CO + ½ O 2 CO 2 H = – 282. 96 k. J 3 CO + 1. 5 O 2 3 CO 2 H = – 848. 88 k. J 2 Fe + 1. 5 O 2 Fe 2 O 3 H = – 822. 14 k. J Don’t forget to add states. For more lessons, visit www. chalkbored. com
1f63ea7cf43b3c960b7440919b0afb60.ppt