Энергетический метод расчёта упругих систем 1 2

Энергетический метод расчёта упругих систем 1

2

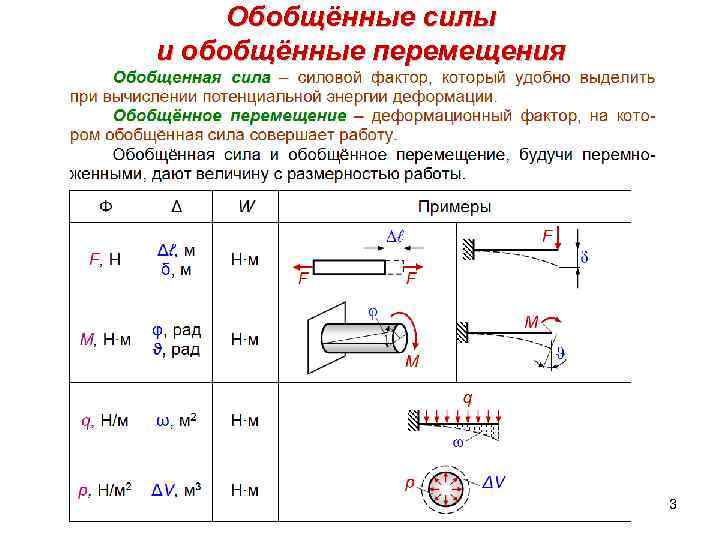Обобщённые силы и обобщённые перемещения 3

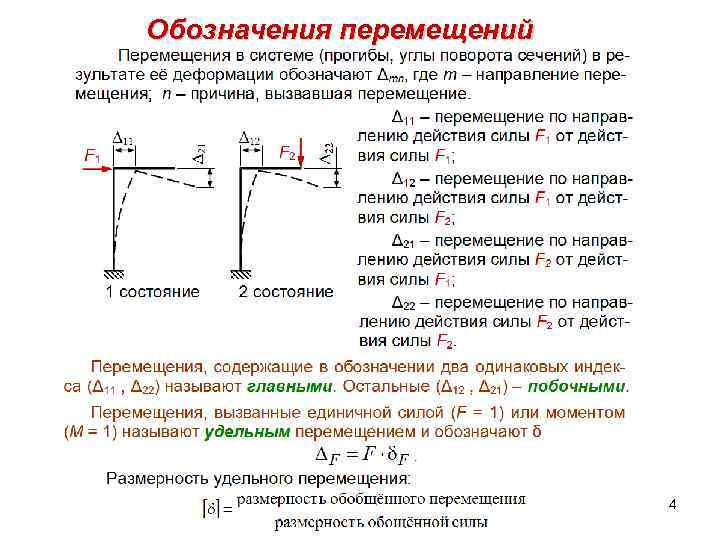Обозначения перемещений 4

Теорема о взаимности работ (теорема Бетти) Рассмотрены два варианта последовательности нагружения системы: 5

Энри ко Бе тти (итал. Enrico Betti, 1823 – 1892) — итальянский математик и физик. Известен своими пионерскими работами по топологии, занимался также абстрактной алгеброй и математическим анализом. Внёс вклад в многомерную теорию связности поверхностей , в теорию потенциала. В физике исследовал проблемы распространения тепла, гидродинамики, теории капиллярности. В теории упругости открыл важную теорему Бетти. С 1862 года – член итальянского парламента, в 1884 году стал сенатором. 6

Теорема о взаимности перемещений (теорема Максвелла) Джеймс Клерк Ма ксвелл (англ. James Clerk Maxwell; 1831 -1879) – британский физик и математик. Член Лондонского королевского общества (1861). Максвелл заложил основы современной классической электродинамики (уравнения Максвелла), ввёл в физику понятия тока смещения и электромагнитного поля, получил ряд следствий из своей теории (предсказание электромагнитных волн, электромагнитная природа света, давление света и другие). Один из основателей кинетической теории газов (установил распределение молекул газа по скоростям). Одним из первых ввёл в физику статистические представления, показал статистическую природу второго начала термодинамики ( «демон Максвелла» ), получил ряд важных результатов в молекулярной физике и термодинамике (термодинамические соотношения Максвелла, правило Максвелла для фазового перехода жидкость — газ и другие). Пионер количественной теории цветов; автор принципа цветной фотографии. Среди других работ Максвелла — исследования по устойчивости колец Сатурна, теории упругости, и механике (фотоупругость, теорема Максвелла), оптике, математике. 7

Метод Максвелла-Мора 8

Христиан Отто Мор (нем. Christian Otto Mohr; 1835 - 1918) – немецкий инженер и учёный в области теоретической механики и сопротивления материалов. Учился в Высшей технической школе в Ганновере. C 1855 года работал над сооружением железных дорог и мостов в Ганновере и Ольденбурге. С 1867 года профессор, сначала в Штутгарте, затем в Дрездене. Занимался проблемами сопротивления материалов. Вывел формулу для определения перемещений в стержневых системах в 1874 г. Предложил в 1882 г. графическое представление напряжённого состояния и на его основе в 1990 г. разработал критерий пластичности и разрушения. 9

Способ Верещагина 10

Способ Верещагина - графоаналитический способ определения перемещений Верещагин Андрей Константинович (1896 — 1959) - физик. В 1918 г. он вступил в РКП (б) и в качестве политработника участвовал в гражданской войне. В 1921 г. А. К. Верещагин поступил в Московский институт инженеров транспорта. В 1924 г. , будучи студентом, предложил правило для вычисления интеграла Максвелла Мора для частного случая прямого стержня постоянного поперечного сечения. После окончания теоретического курса оставил институт и поступил на физико-математический факультет Московского университета, который окончил в 1930 г. Затем он работал в различных научно-исследовательских институтах и стал крупным специалистом в области минной электротехники. В 1937— 1938 гг. преподавал в Военно-морской академии, а в 1947— 1948 гг. — во Всесоюзном заочном энергетическом институте. Во время Великой Отечественной войны Верещагин принимал активное участие в обороне Одессы и Севастополя. В 1956 г. инженер-полковник А. К. Верещагин по состоянию здоровья вышел в отставку. 11

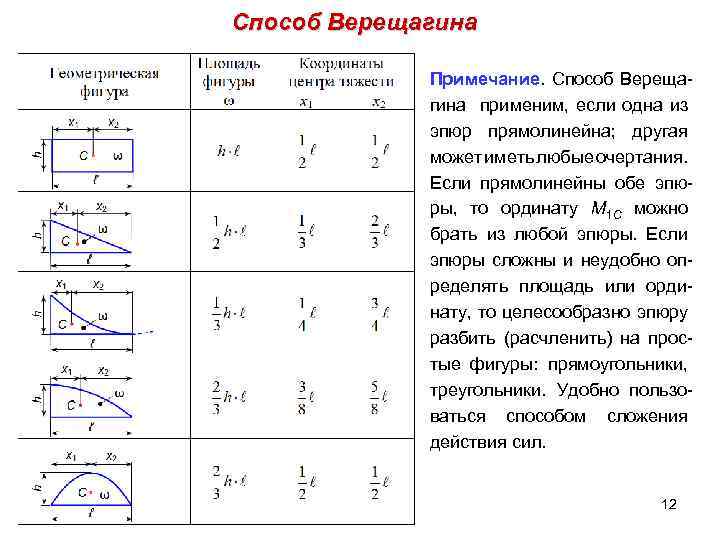Способ Верещагина Примечание. Способ Верещагина применим, если одна из эпюр прямолинейна; другая может иметь любые очертания. Если прямолинейны обе эпюры, то ординату М 1 С можно брать из любой эпюры. Если эпюры сложны и неудобно определять площадь или ординату, то целесообразно эпюру разбить (расчленить) на простые фигуры: прямоугольники, треугольники. Удобно пользоваться способом сложения действия сил. 12

Статически неопределимые системы 13

14

15

Ферма – несущая конструкция, состоящая из прямолинейных стержней, узловые соединения которых при расчёте условно принимаются шарнирными. Фермы применяют главным образом в строительстве (покрытия зданий, пролётные строения мостов, мачты, опоры линий электропередачи, гидротехнические 16 затворы и др. ), а также в качестве несущих конструкций машин и механизмов.

Рама – стержневая система, элементы которой (стойки, ригели, подкосы) во всех или в некоторых узлах жестко соединены между собой. Рамы служат в основном несущими конструкциями зданий, мостов, эстакад и др. сооружений, а также рабочих 17 и транспортных машин.

ВОЗДУШНЫЕ ГИМНАСТЫ НА ТРАПЕЦИЯХ Различают рамы пространственные и плоские Плоская система – система конструкций, в которой оси симметрии всех элементов и линии действия внешних сил находятся в одной плоскости. 18

19

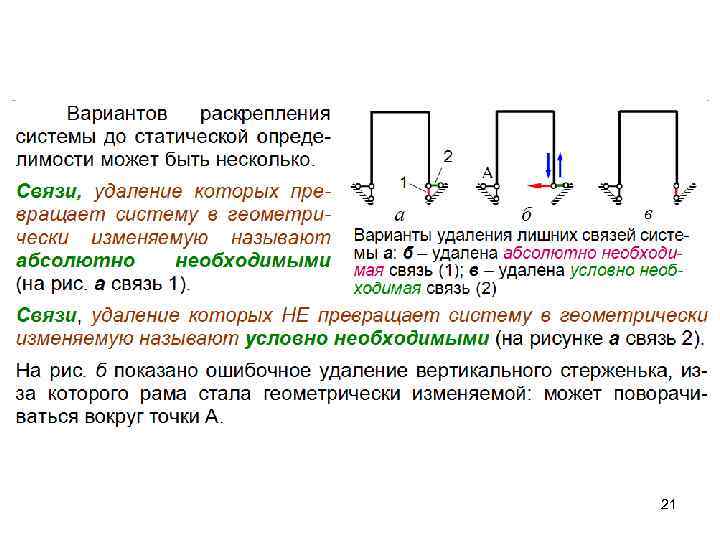
Раскрытие статической неопределимости методом сил 20

21

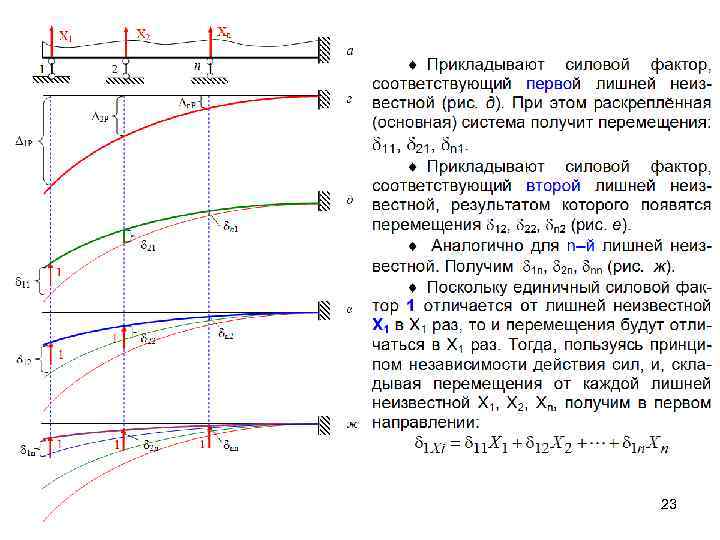
Канонические уравнения метода сил 22

23

Канонические уравнения метода сил 24

Коэффициенты канонических уравнений метода сил 25

Коэффициенты канонических уравнений метода сил 26