ENCE 710 Design of Steel Structures VI Plate

ENCE 710 Design of Steel Structures VI. Plate Girders C. C. Fu, Ph. D. , P. E. Civil and Environmental Engineering Department University of Maryland

Introduction Following subjects are covered: n Moment strength n Shear strength n Intermediate transverse stiffener n Bearing stiffener Reading: n Chapters 11 of Salmon & Johnson n AISC LRFD Specification Chapters B (Design Requirements) and F (Design of Members for Flexure) and G (Design of Members for Shear) 2

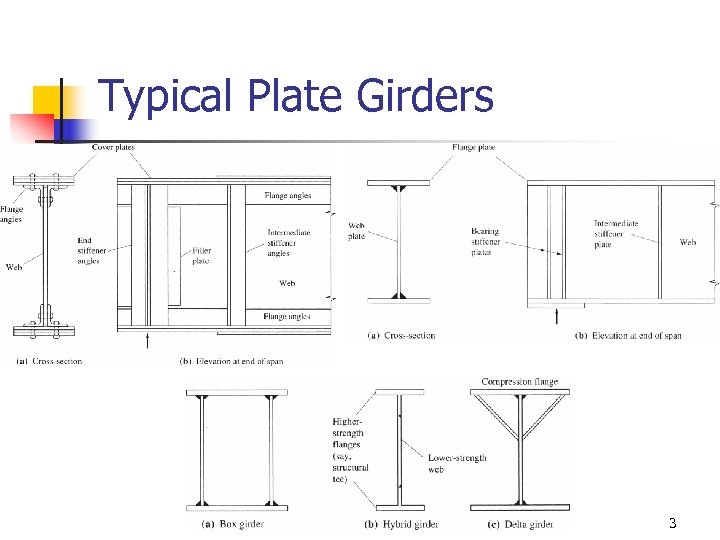Typical Plate Girders 3

AISC Limiting Ratios 4

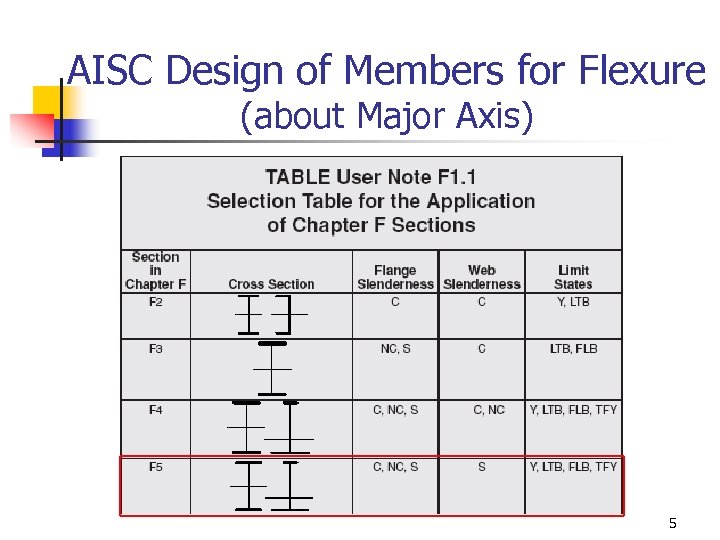AISC Design of Members for Flexure (about Major Axis) 5

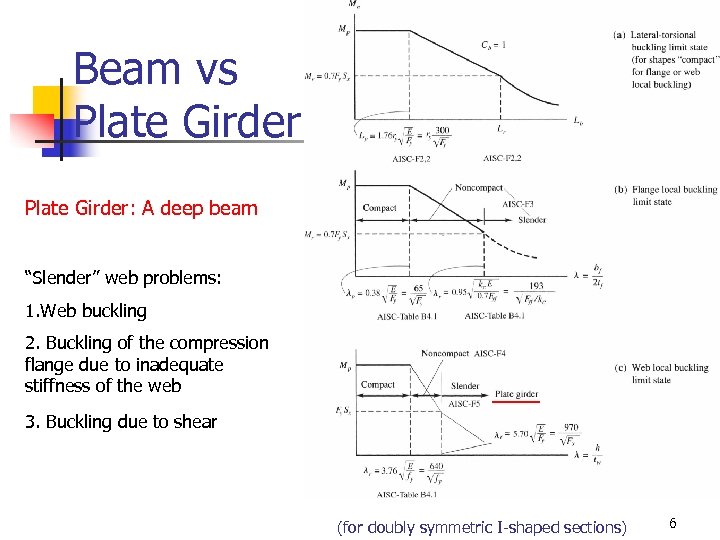Beam vs Plate Girder: A deep beam “Slender” web problems: 1. Web buckling 2. Buckling of the compression flange due to inadequate stiffness of the web 3. Buckling due to shear (for doubly symmetric I-shaped sections) 6

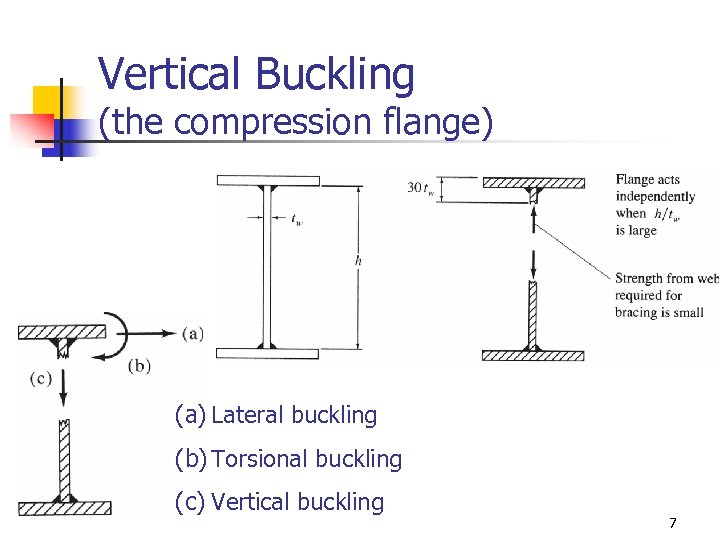Vertical Buckling (the compression flange) (a) Lateral buckling (b) Torsional buckling (c) Vertical buckling 7

AISC Maximum Web h/tw n n Stiffened girder (for a/h ≤ 1. 5) h/tw = 11. 7 √E/Fy (AISC-F 13. 3) Stiffened girder (for a/h > 1. 5) h/tw ≤ 0. 42 E/Fy (AISC-F 13. 4) (S & J Table 11. 3. 1) n Unstiffened girder h/tw ≤ 260 8

AISC Nominal Moment Strength n n If h/tw ≤ 5. 70√E/Fy – AISC Table B 4. 1 treated as rolled beams If h/tw > 5. 70√E/Fy n Case 1 – Compression flange yielding Mn = Rpg. Fy. Sxc n (F 5 -1) Mn = Rpg. Fcr. Sxc (a) Lp < L b ≤ Lr (F 5 -2) (F 5 -3) Case 2 – Lateral-Torsional Buckling (b) Lb > Lr (F 5 -4, 5, 6) (for WLB) aw = ratio of web area to compression flange area ( ≤ 10) hc = 2 x centroid to inside face of the compression flange 9

AISC Nominal Moment Strength (cont. ) n Case 3 - Compression flange local buckling Mn = Rpg. Fcr. Sxc Fcr a. λ ≤ λp: Fcr = Fy b. λ p < λ ≤ λr : (F 5 -7) (F 5 -8) c. λ > λr : kc = 4/√(h/tw) n and Case 4 – Tension-flange yielding (Sxt

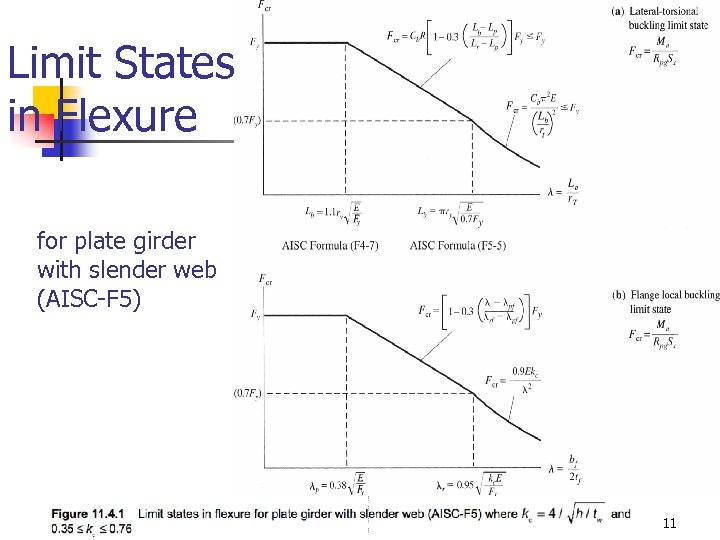Limit States in Flexure for plate girder with slender web (AISC-F 5) 11

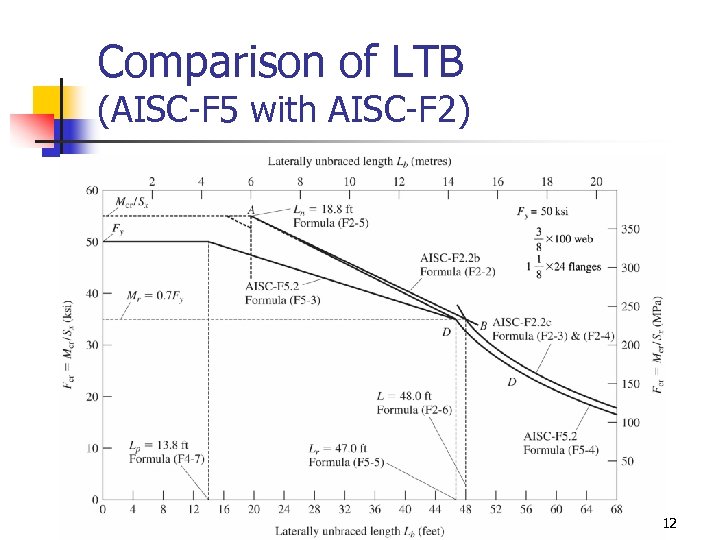Comparison of LTB (AISC-F 5 with AISC-F 2) 12

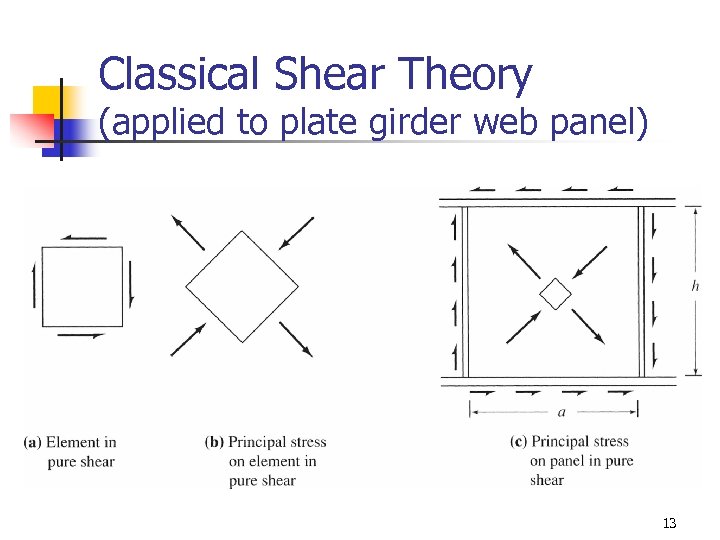Classical Shear Theory (applied to plate girder web panel) 13

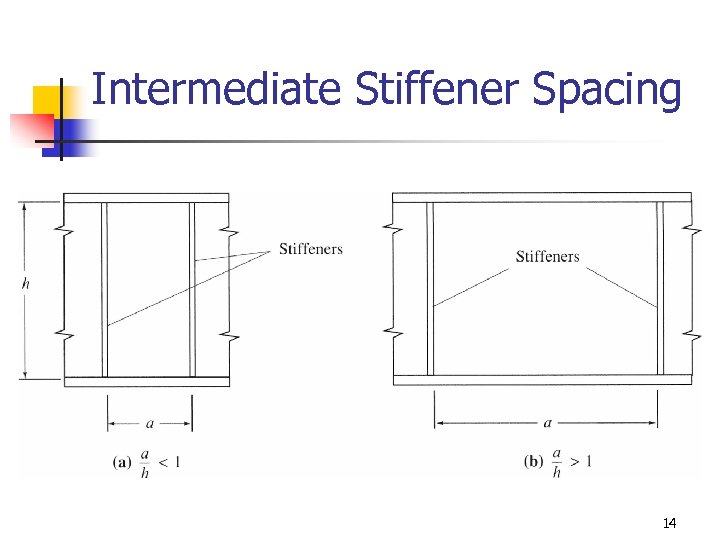Intermediate Stiffener Spacing 14

AISC Nominal Shear Strength n If h/tw ≤ 1. 10 √(kv. E/Fy) - Vn = 0. 6 Aw. Fy same as rolled beam n (G 3 -1) If h/tw > 1. 10 √(kv. E/Fy) (G 3 -2) Except (1) (2) (S & J Figs. 11. 8. 1 & 11. 8. 2) end panel a/h > 3 or a/h > [260/(h/tw)]2 15

AISC Nominal Shear Strength (cont. ) n For 1. 10 √(kv. E/Fy) ≤ h/tw ≤ 1. 37 √(kv. E/Fy) Cv = 1. 10 √(kv. E/Fy) / (h/tw) n (G 2 -4) For h/tw > 1. 37 √(kv. E/Fy) Cv = 1. 51 kv. E/[(h/tw)2 Fy] kv = 5 + 5/(a/h)2 5 (G 2 -5) if a/h ≤ 3 and [260/(h/tw)]2 otherwise (S & J Fig. 11. 8. 3) 16

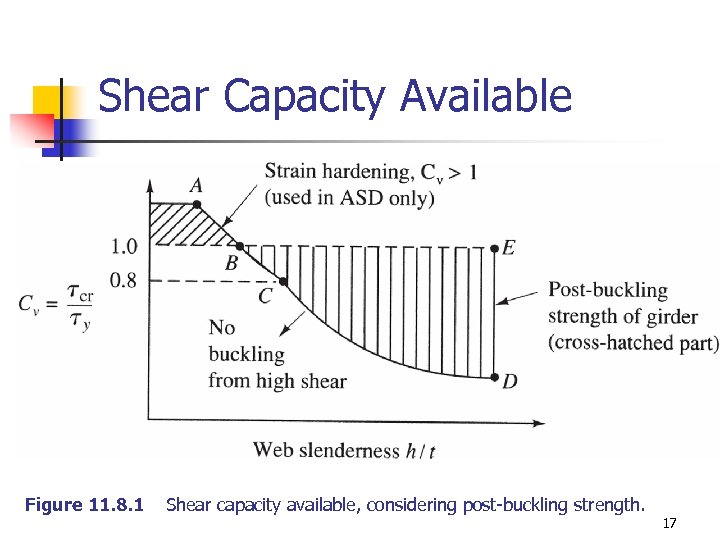Shear Capacity Available Figure 11. 8. 1 Shear capacity available, considering post-buckling strength. 17

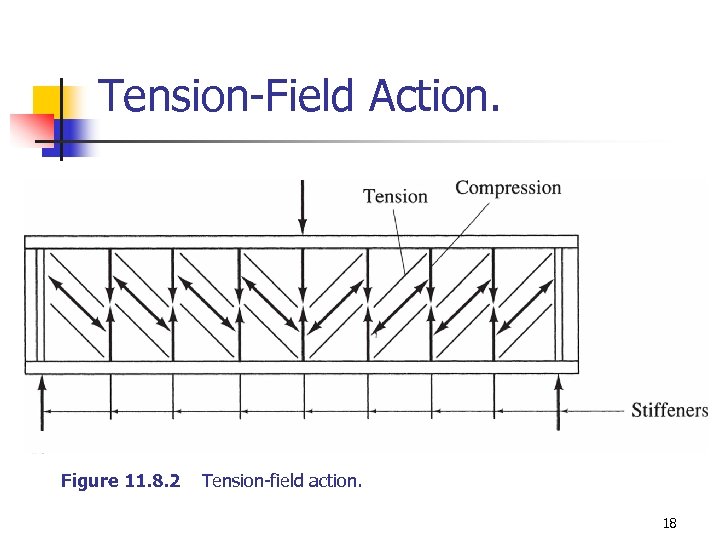Tension-Field Action. Figure 11. 8. 2 Tension-field action. 18

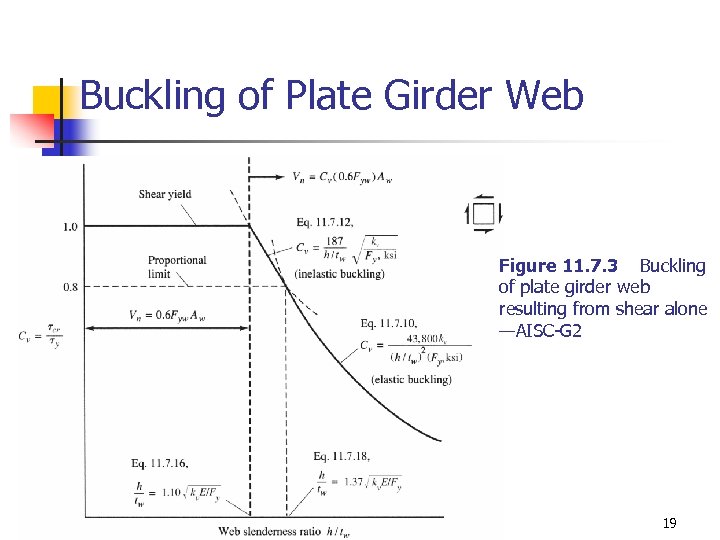Buckling of Plate Girder Web Figure 11. 7. 3 Buckling of plate girder web resulting from shear alone —AISC-G 2 19

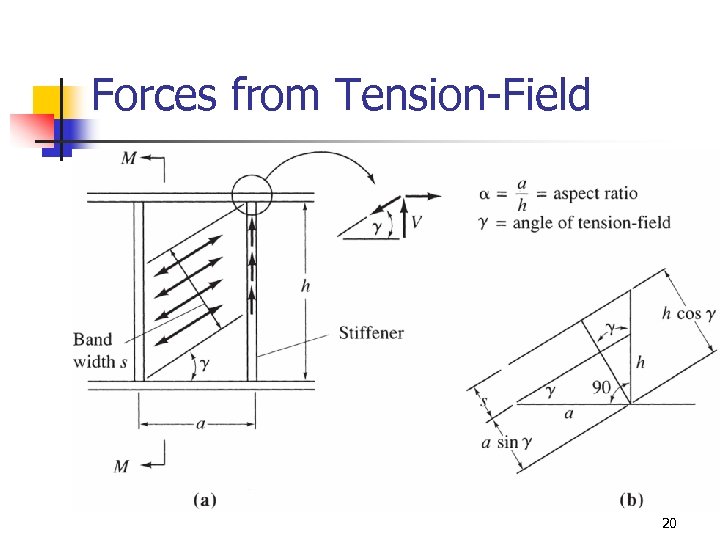Forces from Tension-Field 20

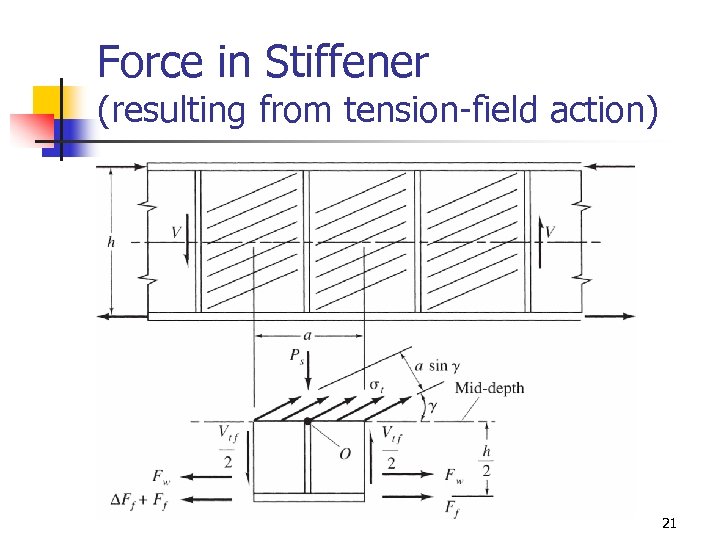Force in Stiffener (resulting from tension-field action) 21

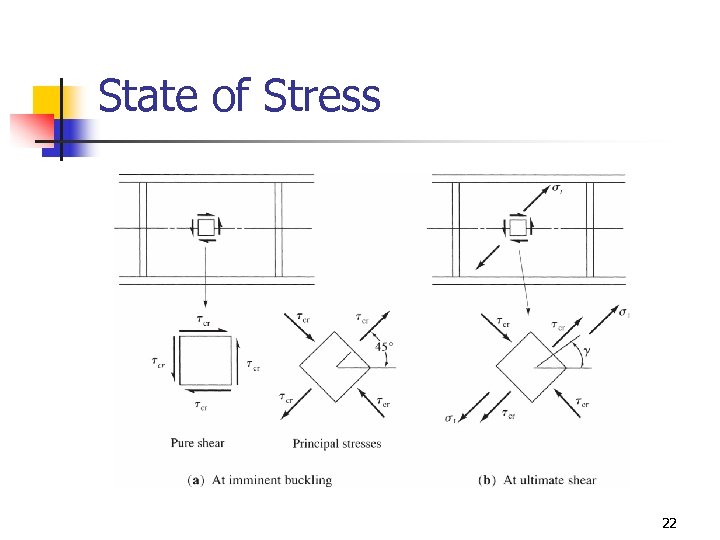State of Stress 22

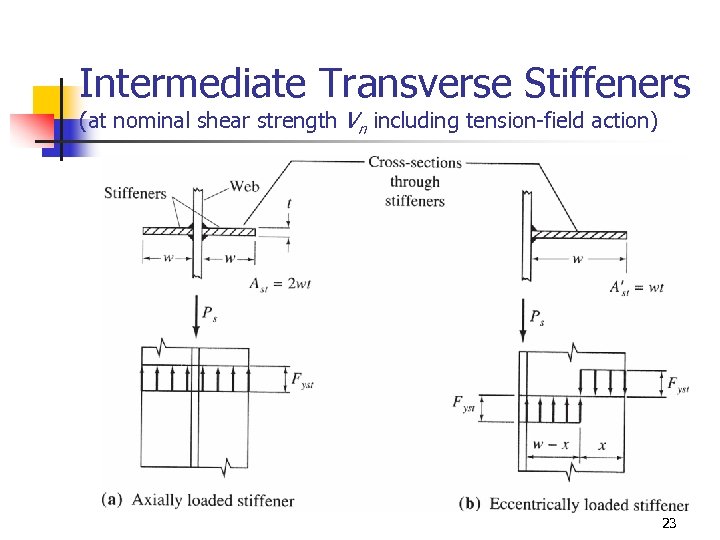Intermediate Transverse Stiffeners (at nominal shear strength Vn including tension-field action) 23

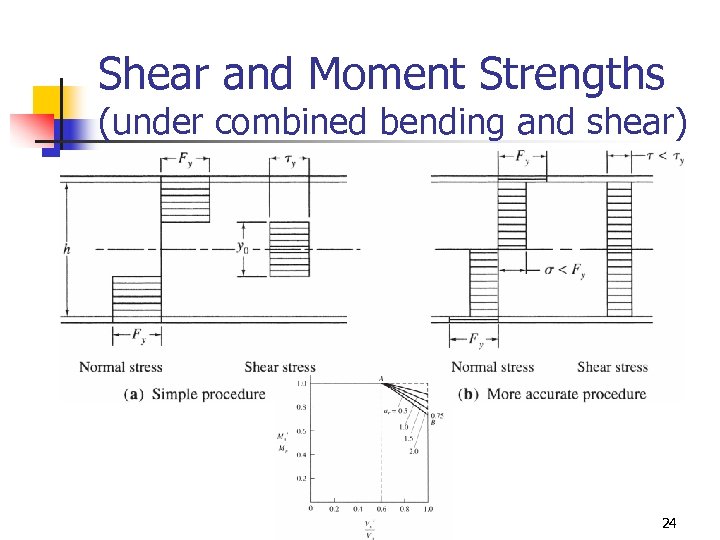Shear and Moment Strengths (under combined bending and shear) 24

Intermediate Transverse Stiffeners Intermediate Transverse Stiffener (not required if h/tw ≤ 2. 45√E/Fy) (1) Stiffness Criterion Ist ≥ jatw 3 (G 2 -6) where j = 2. 5/(a/h)2 – 2 ≥ 0. 5 n (2) Strength Criterion n Ast > Fy/Fyst (0. 15 Dshtw (1 – Cv) Vu/Φv. Vn – 18 tw 2)≤ 0 (G 3 -3) 25

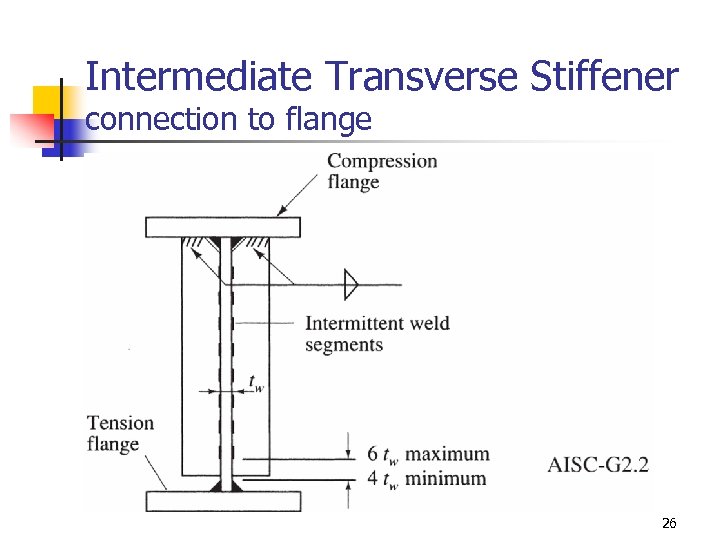Intermediate Transverse Stiffener connection to flange 26

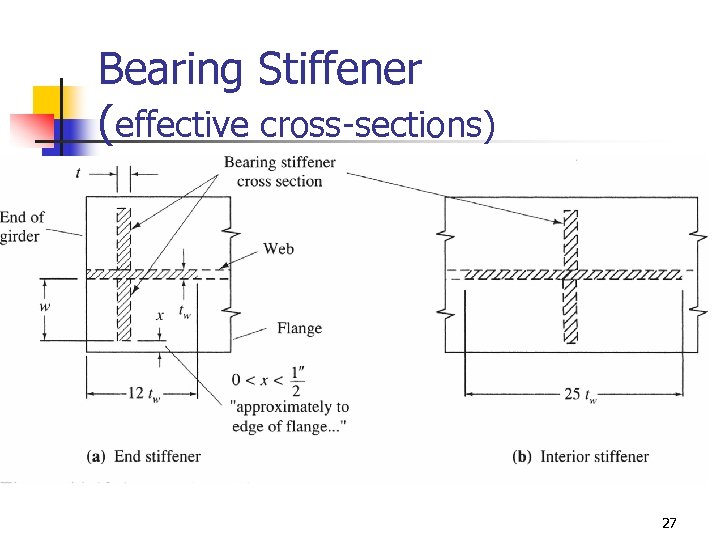Bearing Stiffener (effective cross-sections) 27

Bearing Stiffener ΦRn ≥ Ru (1) Bearing Criterion (LRFD – J 8. 1) Φ = 0. 75 Rn= 1. 8 Fy. Apb (2) Column Stability Criterion KL/r = 0. 75 h/r where r of 12 tw or 25 tw Φc. Fcr = LRFD Table 3 -36 Reqd. Ast = Ru/Φc. Fcr → Reqd. t (3) Local Buckling Criterion (AISC 13 th Edition Table B 4. 1 Case 3) Min. t = w/(0. 56/√E/Fy) 28

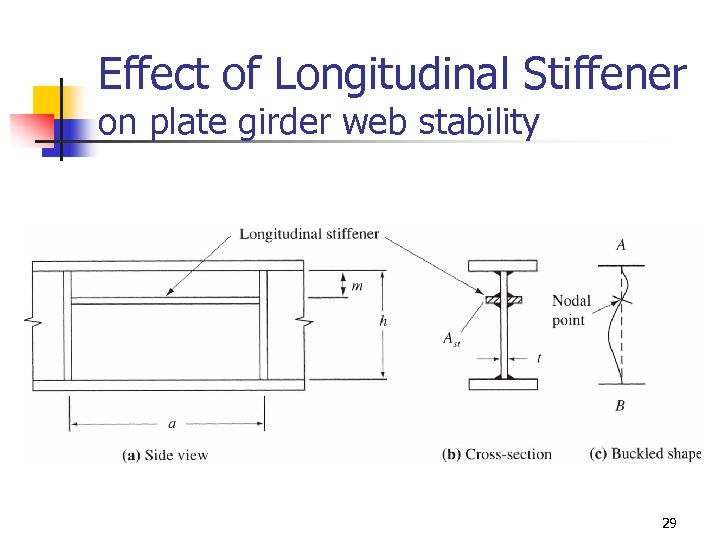Effect of Longitudinal Stiffener on plate girder web stability 29

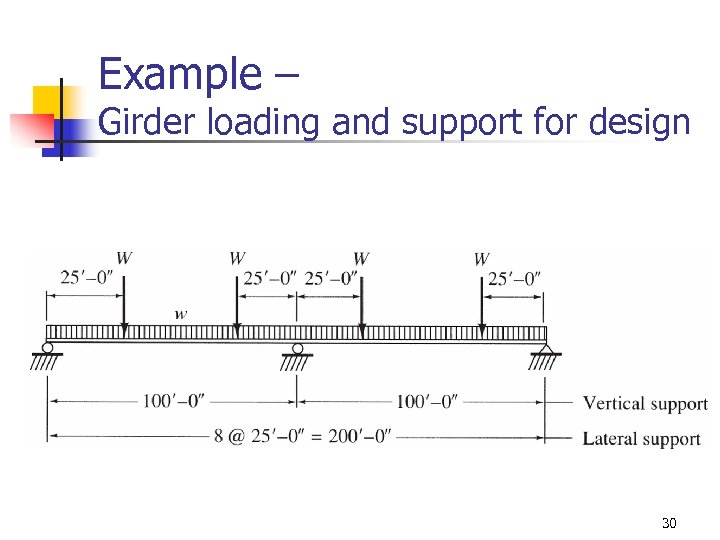Example – Girder loading and support for design 30

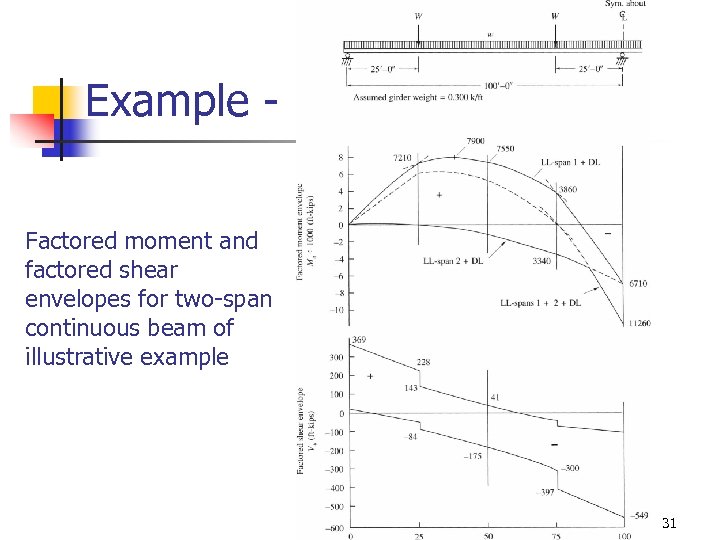Example Factored moment and factored shear envelopes for two-span continuous beam of illustrative example 31

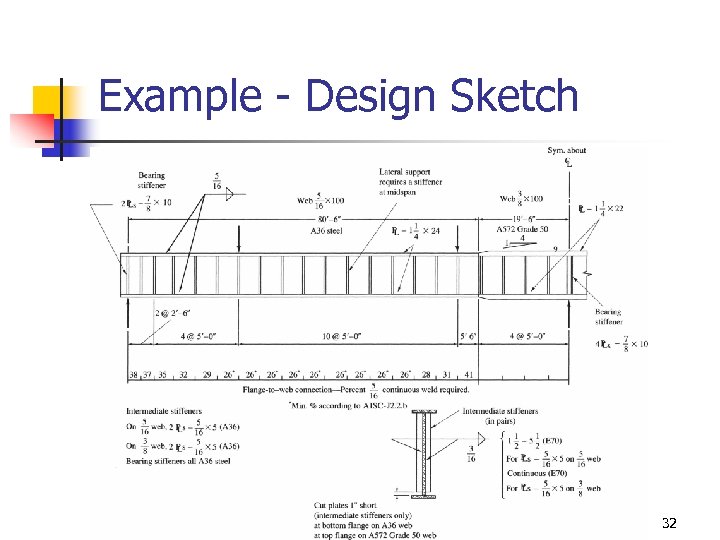Example - Design Sketch 32