Эмпирические распределения 1 2 3 4 Вариационный

Эмпирические распределения

1. 2. 3. 4. Вариационный ряд и его графическая интерпретация Метод средних величин Генеральная и выборочная совокупности. Способы организации выборки Выборочный метод. Доверительный интервал

Группа чисел, относящихся к одному и тому же признаку, называется статистической совокупностью Каждый элемент совокупности называется вариантой – Хi Количество повторений вариант в совокупности называется частотой – ni Количество элементов в совокупности (сумма частот) называется объемом совокупности – n

1. Ранжирование – запись данных в порядке возрастание или убывания 2. Запись данных в виде вариационного ряда. Это двойной числовой ряд, где в один столбец (строку) записываются варианты, а в другой столбец (строку) их частоты соответственно. Вариационные ряды бывают: - интервальными - безинтервальными

У спортсменов зарегистрировано время восстановления пульса после прохождения дистанции (с): 81, 78, 84, 90, 78, 81, 74, 90, 74, 81, 84, 81, 90, 81 Объем совокупности – n = 14

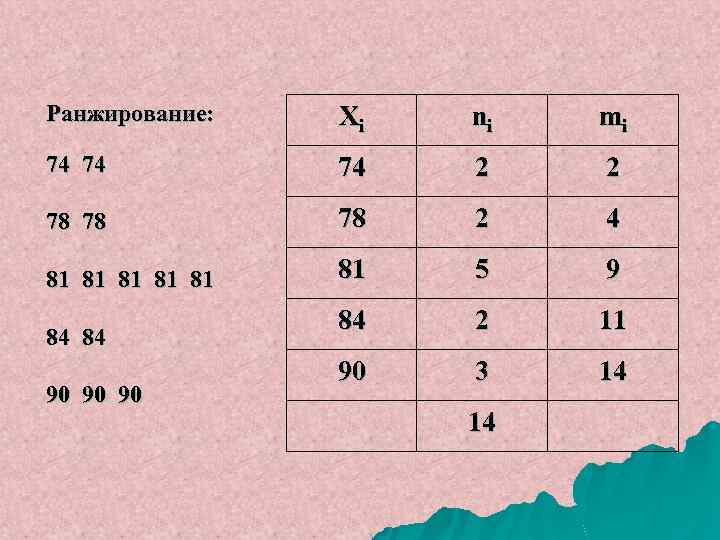Ранжирование: Xi ni mi 74 74 74 2 2 78 78 78 2 4 81 81 81 5 9 84 2 11 90 3 14 84 84 90 90 90 14

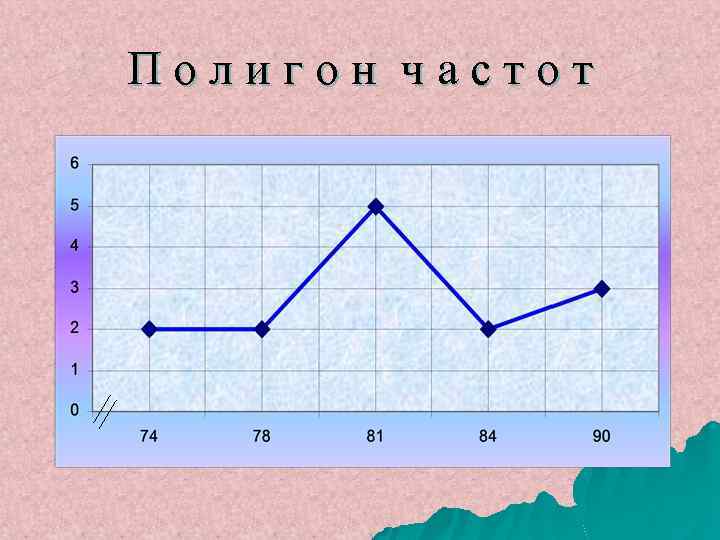Полигон частот

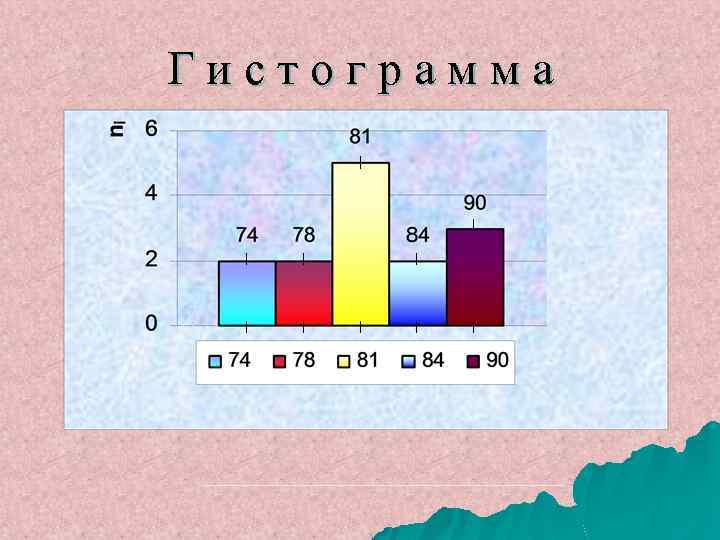Гистограмма

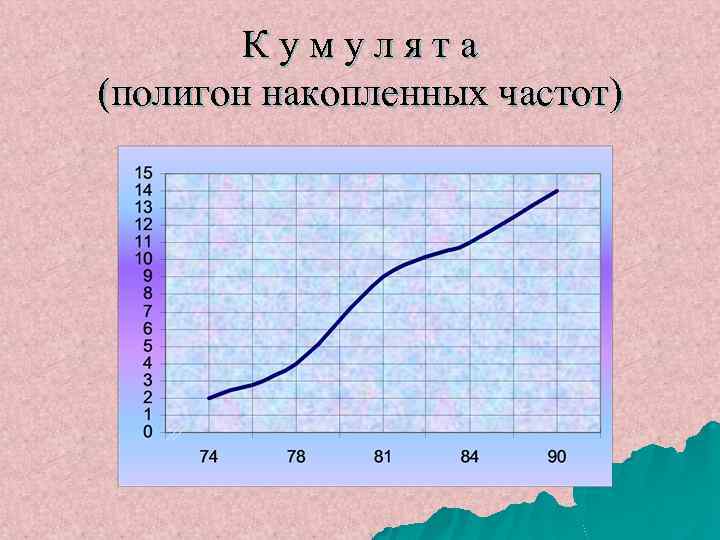Кумулята (полигон накопленных частот)

Характеристики (параметры) вариационного ряда Среднее арифметическое – такое значение признака, сумма отклонений от которого всех остальных значений равна нулю с учетом знака отклонения

Мода – вариант, который имеет наибольшую частоту, т. е. чаще всего встречается в нашей совокупности Медиана – вариант, который делит вариационный ряд пополам, т. е. соответствует средней частоте Если мода и медиана равны или близки по значению среднему арифметическому, то группу данных можно считать однородной

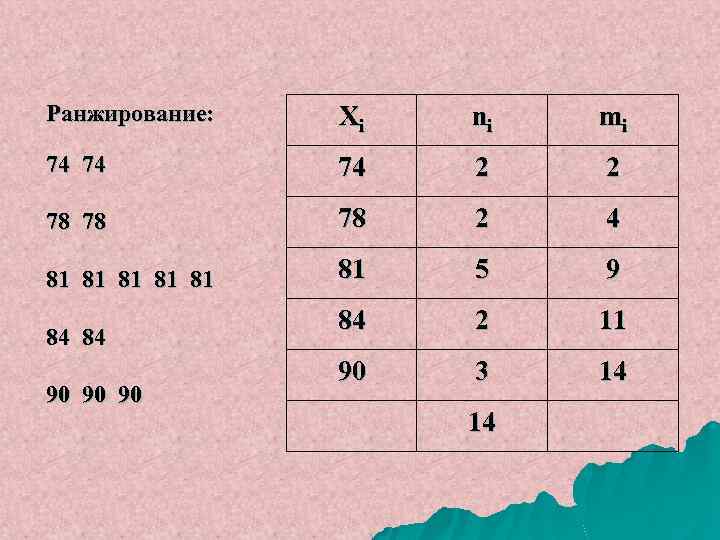Ранжирование: Xi ni mi 74 74 74 2 2 78 78 78 2 4 81 81 81 5 9 84 2 11 90 3 14 84 84 90 90 90 14

Дисперсия – средний квадрат отклонений значений признака от среднего арифметического Если n>=30, то делим на n, Если n<30, то делим на (n - 1)

Среднее квадратическое отклонение (стандартное отклонение) Дисперсия и стандартное отклонение показывают рассеивание эмпирических данных вокруг среднего арифметического

Коэффициент вариации – показывает какую часть среднее квадратическое отклонение (рассеивание) составляет от среднего арифметического в процентах Если V <= 10% - статистическую совокупность можно считать однородной Если V > 10% - статистическую совокупность считают неоднородной

Метод средних величин позволяет производить анализ и разделение с помощью характеристик вариационных рядов, а также решать задачи на нормирование и сравнение признаков

Пример: Чтобы проверить ловкость поступающих в секцию баскетбола, им предложили преодолеть бегом определенный маршрут с ведением мяча и у 20 человек зафиксировали время – Хi (c). 20, 28, 20, 24, 24, 12, 18, 30, 20, 20 24, n = 20 28, 30, 20, 18,

Записываем вариационный ряд и рассчитываем его характеристики xi ni xi* ni (xi-x)2*ni 12 1 12 - 11 121 18 2 36 -5 25 50 20 7 140 -3 9 63 24 5 120 1 1 5 28 2 56 5 25 50 30 3 90 7 49 147 20 454 436

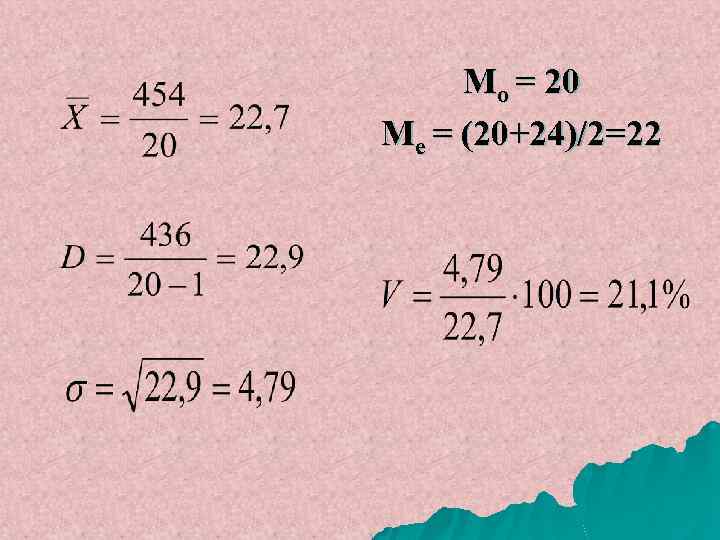Мо = 20 Ме = (20+24)/2=22

Генеральная совокупность – наиболее общая совокупность объектов, объединенная каким-либо признаком Выборочная совокупность (выборка) – часть генеральной, которая подлежит исследованию

Существуют два требования при составления выборки: u Все элементы выборки должны быть подобраны случайно; u Количество элементов в выборке должно быть таким, чтобы она достаточно представляла генеральную совокупность и, в тоже время, не осложняло исследования.

Способы организации выборки: u Жеребьевка (повторный и бесповторный способ) u Механический отбор u Типический отбор u Серийный отбор u С помощью таблицы случайных чисел

Для выполнения второго условия необходимо знать следующее: Если в выборке меньше 10 элементов (n<=10), то она не может представлять генеральную совокупность u Если в выборке 20 элементов, то она может представлять генеральную совокупность, но только в том случае когда эта совокупность распределена в соответствии с нормальным законом u Только при объеме выборки равном 30 (n=30) она может достаточно представлять генеральную совокупность u

Основная задача выборочного метода – нахождение средних значений (среднее арифметическое и среднее квадратическое отклонение) генеральной совокупности по средним значениям выборочной

Как бы хорошо выборка не представляла генеральную совокупность, их средние значения не будут равны

Вычисляем ошибку репрезентативности, которая показывает величину различия между средними значениями генеральной и выборочной совокупности Если n>=30, то делим на n, Если n<30, то делим на (n - 1)

Надежность (доверительная вероятность) – вероятность, с которой гарантируется точность расчетов при определении средних значений генеральной совокупности по средним выборочной мы рассматриваем три уровня надежности: u Р = 0, 95 u Р = 0, 999

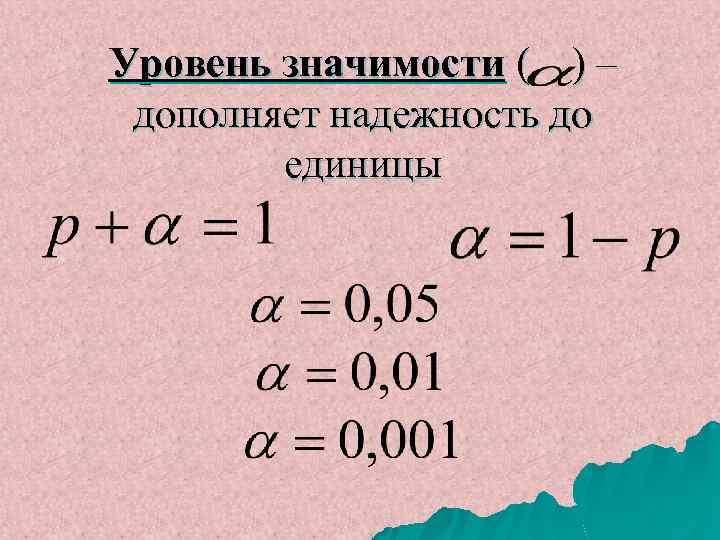Уровень значимости ( ) – дополняет надежность до единицы

Английский математик Вильям Госсет, известный под псевдонимом Стьюдент определил взаимосвязь между объемом выборки и доверительной вероятностью Для каждого уровня надежности в специальных таблицах представлен критерий надежности (t) – величина, которая показывает взаимосвязь между объемом выборки и доверительной вероятностью

Произведение ошибки репрезентативности на критерий Стьюдента (m · t) – абсолютная погрешность вычислений Интервал, в котором с заданной надежностью находится оцениваемый генеральный параметр (среднее арифметическое или стандартное отклонение) называется доверительным интервалом Доверительный интервал можно использовать как основу для модельной характеристики

Пример. Подготовить основу для модельной характеристики функциональных систем легкоатлетов бегунов на 1500 м (І разряд) по показанию жизненной емкости легких (ЖЕЛ) – Хі , л, у 30 легкоатлетов аналогичной специализации 5, 46 5, 42 5, 35 5, 16 5, 35 5, 21 5, 35 5, 10 5, 35 5, 21 5, 42 5, 16 5, 35 5, 21 5, 50 5, 35 5, 42 5, 35 5, 21 5, 10 5, 46 5, 16 5, 46 5, 21 5, 46

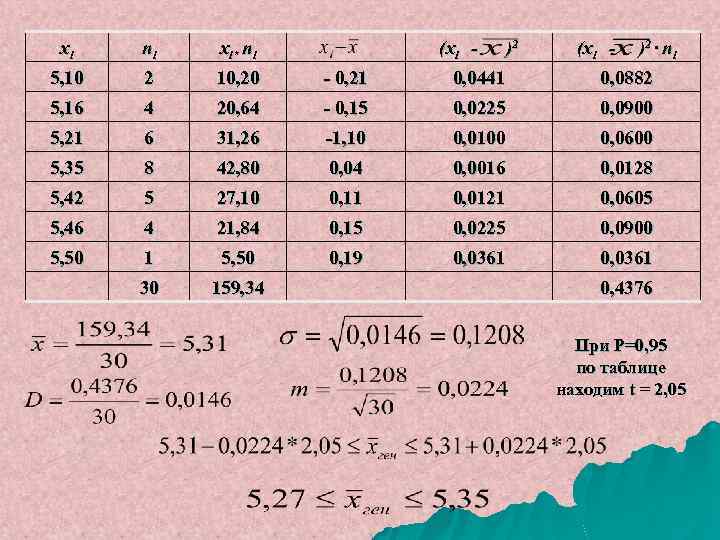xi ni xi* ni (xi - )2 · n i 5, 10 2 10, 20 - 0, 21 0, 0441 0, 0882 5, 16 4 20, 64 - 0, 15 0, 0225 0, 0900 5, 21 6 31, 26 -1, 10 0, 0100 0, 0600 5, 35 8 42, 80 0, 04 0, 0016 0, 0128 5, 42 5 27, 10 0, 11 0, 0121 0, 0605 5, 46 4 21, 84 0, 15 0, 0225 0, 0900 5, 50 1 5, 50 0, 19 0, 0361 30 159, 34 0, 4376 При Р=0, 95 по таблице находим t = 2, 05