0f8c95d2810600acc20bbd00f8cb638f.ppt
- Количество слайдов: 31
 Empirical Likelihood for Right Censored and Left Truncated data Jingyu (Julia) Luan University of Kentucky, Johns Hopkins University March 30, 2004
Empirical Likelihood for Right Censored and Left Truncated data Jingyu (Julia) Luan University of Kentucky, Johns Hopkins University March 30, 2004
 Outline of the Presentation: • Part I: Introduction and Background • Part II: Empirical Likelihood Theorem for Right-Censored and Left-Truncated Data • Part III: Future Research
Outline of the Presentation: • Part I: Introduction and Background • Part II: Empirical Likelihood Theorem for Right-Censored and Left-Truncated Data • Part III: Future Research
 Part I: Introduction and Background n 1. 1 Empirical Likelihood Ratio Test n 1. 2 Censoring and Truncation n 1. 3 n Literature Review 1. 4 Counting Process and Survival Analysis
Part I: Introduction and Background n 1. 1 Empirical Likelihood Ratio Test n 1. 2 Censoring and Truncation n 1. 3 n Literature Review 1. 4 Counting Process and Survival Analysis
 1. 1 Empirical Likelihood Ratio Test: Two cases: A. Parametric B. Non-parametric
1. 1 Empirical Likelihood Ratio Test: Two cases: A. Parametric B. Non-parametric
 1. 1 Empirical Likelihood Ratio Test Parametric situation: Wilks (1938): -2 log. R has an asymptotic p 2 distribution under null hypothesis. .
1. 1 Empirical Likelihood Ratio Test Parametric situation: Wilks (1938): -2 log. R has an asymptotic p 2 distribution under null hypothesis. .
 1. 1 Empirical Likelihood Ratio Test Nonparametric situation: n Empirical Likelihood is defined as (Owen 1988): Where X 1, X 2, …, Xn are independent random variables from an unknown distribution F. And it is well known that L(F) is maximized by the empirical distribution function Fn over all possible CDFs, where
1. 1 Empirical Likelihood Ratio Test Nonparametric situation: n Empirical Likelihood is defined as (Owen 1988): Where X 1, X 2, …, Xn are independent random variables from an unknown distribution F. And it is well known that L(F) is maximized by the empirical distribution function Fn over all possible CDFs, where
 1. 1 Empirical Likelihood Ratio Test n Owen focused on studying the properties of the for a given g(. ). likelihood ratio function when F 0 satisfies certain constraint, (the null hypothesis)
1. 1 Empirical Likelihood Ratio Test n Owen focused on studying the properties of the for a given g(. ). likelihood ratio function when F 0 satisfies certain constraint, (the null hypothesis)
 1. 1 Empirical Likelihood Ratio Test n Owen defined the empirical likelihood ratio function as where L(F|θ) is the maximized empirical likelihood function among all CDFs satisfying the above constraint (null hypothesis). Owen (1988) demonstrated when θ=θ 0, -2 log. R(F|θ) has an asymptotic χ2 distribution with df=1.
1. 1 Empirical Likelihood Ratio Test n Owen defined the empirical likelihood ratio function as where L(F|θ) is the maximized empirical likelihood function among all CDFs satisfying the above constraint (null hypothesis). Owen (1988) demonstrated when θ=θ 0, -2 log. R(F|θ) has an asymptotic χ2 distribution with df=1.
 1. 2 Censoring and Truncation n n Survival analysis is the analysis of time-to-event data. Two important features of time-to-event data: A. Censoring B. Truncation
1. 2 Censoring and Truncation n n Survival analysis is the analysis of time-to-event data. Two important features of time-to-event data: A. Censoring B. Truncation
 1. 2 Censoring and Truncation n Censoring occurs when an individual’s life length is known to happen only in a certain period of time. A. Right Censoring B. Left Censoring C. Interval Censoring
1. 2 Censoring and Truncation n Censoring occurs when an individual’s life length is known to happen only in a certain period of time. A. Right Censoring B. Left Censoring C. Interval Censoring
 1. 2 Censoring and Truncation n Truncation A. Left Truncation: it occurs when subjects enter a study at a particular time and are followed from this delayed entry time until the event happens or until the subject is censored; B. Right Truncation: it occurs when only individuals who have experienced the event of interest are included in the sample.
1. 2 Censoring and Truncation n Truncation A. Left Truncation: it occurs when subjects enter a study at a particular time and are followed from this delayed entry time until the event happens or until the subject is censored; B. Right Truncation: it occurs when only individuals who have experienced the event of interest are included in the sample.
 1. 2 Censoring and Truncation n Example of Right-Censored and Left-Truncated data: [Klein, Moeschberger, p 65] In a survival study of the Channing House retirement center located in California, ages at which individuals entered the retirement community (truncation event) and ages when members of the community died or still alive at the end of the study (censoring event) were recorded.
1. 2 Censoring and Truncation n Example of Right-Censored and Left-Truncated data: [Klein, Moeschberger, p 65] In a survival study of the Channing House retirement center located in California, ages at which individuals entered the retirement community (truncation event) and ages when members of the community died or still alive at the end of the study (censoring event) were recorded.
 1. 3 Literature Review n n Product limit estimator (based on right censored and left truncated data) of survival function: an analogue of the Kaplan-Meier estimator of survival function under censoring; For solely truncation data, Wang and Jewell (1985) and Woodroofe (1985) independently proved consistency results for the product limit estimator and showed weak convergence to a Brownian Motion process;
1. 3 Literature Review n n Product limit estimator (based on right censored and left truncated data) of survival function: an analogue of the Kaplan-Meier estimator of survival function under censoring; For solely truncation data, Wang and Jewell (1985) and Woodroofe (1985) independently proved consistency results for the product limit estimator and showed weak convergence to a Brownian Motion process;
 1. 3 Literature Review n n Wang, Jewell, and Tsai (1987): described a description of the asymptotic behavior of the product limit estimator for right censoring and left truncation data For pure truncated data, Li (1995) studied the empirical likelihood theorem.
1. 3 Literature Review n n Wang, Jewell, and Tsai (1987): described a description of the asymptotic behavior of the product limit estimator for right censoring and left truncation data For pure truncated data, Li (1995) studied the empirical likelihood theorem.
 1. 3 Literature Review For solely censoring data: n Pan and Zhou (1999) showed that the empirical likelihood ratio with continuous mean and hazard constraint also have a chi-square limit. n Fang (2000) proved the empirical likelihood ratio with discrete hazard constraint follows a chisquare distribution under one sample case and two sample case.
1. 3 Literature Review For solely censoring data: n Pan and Zhou (1999) showed that the empirical likelihood ratio with continuous mean and hazard constraint also have a chi-square limit. n Fang (2000) proved the empirical likelihood ratio with discrete hazard constraint follows a chisquare distribution under one sample case and two sample case.
 1. 4 Counting Process and Survival Analysis n n Counting process provides an elegant martingale based approach to study time-to-event data. Martingale methods can be used to obtain simple expressions for the moments of complicated statistics and to calculate and verify asymptotic distributions for test statistics and estimators.
1. 4 Counting Process and Survival Analysis n n Counting process provides an elegant martingale based approach to study time-to-event data. Martingale methods can be used to obtain simple expressions for the moments of complicated statistics and to calculate and verify asymptotic distributions for test statistics and estimators.
 Part II: Empirical Likelihood Theorem for Right -Censored and Left-Truncated Data u 2. 1 One Sample Case u 2. 2 Two Sample Case
Part II: Empirical Likelihood Theorem for Right -Censored and Left-Truncated Data u 2. 1 One Sample Case u 2. 2 Two Sample Case
 Part III: One Sample Case First, introduce some notations:
Part III: One Sample Case First, introduce some notations:
 Part III: One Sample Case u Then, the likelihood function is:
Part III: One Sample Case u Then, the likelihood function is:
 Part III: One Sample Case
Part III: One Sample Case
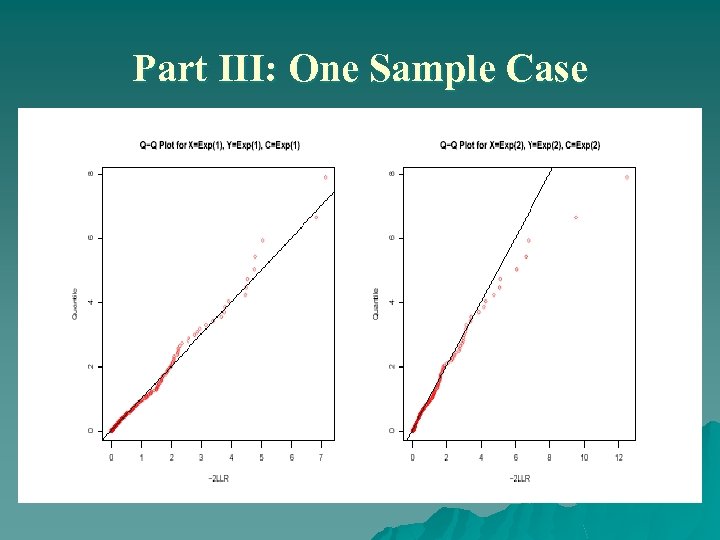 Part III: One Sample Case
Part III: One Sample Case
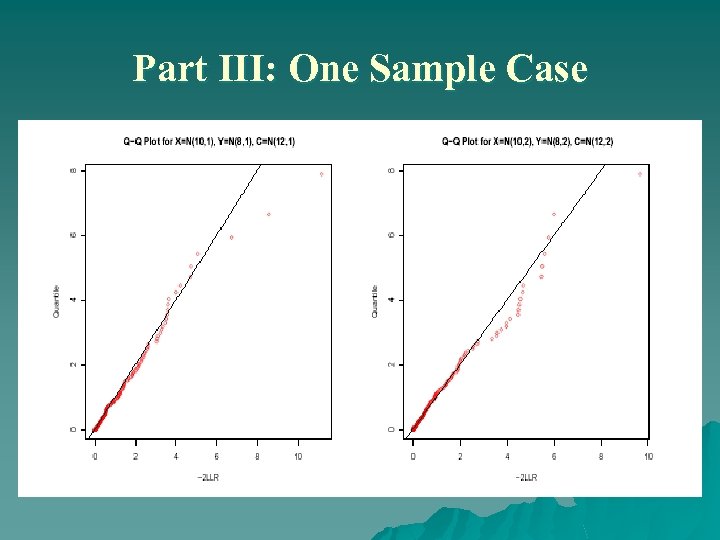 Part III: One Sample Case
Part III: One Sample Case
 Part III: Two Sample Case
Part III: Two Sample Case
 Part III: Future research The same setting as one sample case. Under k constraints:
Part III: Future research The same setting as one sample case. Under k constraints:
 Part III: Future research Let be k observed samples.
Part III: Future research Let be k observed samples.
 Part III: Future research
Part III: Future research
 Part III: Future Research u Owen (1991) has demonstrated that empirical likelihood ratio can be applied to regression models. u However, for censored/truncated data the empirical likelihood results are rare. Exception: Li (2002). u Notice we are talking about ordinary regression model, not the Cox proportional hazards regression model.
Part III: Future Research u Owen (1991) has demonstrated that empirical likelihood ratio can be applied to regression models. u However, for censored/truncated data the empirical likelihood results are rare. Exception: Li (2002). u Notice we are talking about ordinary regression model, not the Cox proportional hazards regression model.
 Part III: Regression models u We propose a “redistribution” algorithm of estimating the parameters in the regression models with censored/truncated data. u We think the Empirical likelihood method can be used there to do inference.
Part III: Regression models u We propose a “redistribution” algorithm of estimating the parameters in the regression models with censored/truncated data. u We think the Empirical likelihood method can be used there to do inference.
 Reference:
Reference:
 Reference:
Reference:
 Acknowledgement Dr. Mai Zhou Dr. Arne Bathke Dr. William Griffith Dr. William Rayens Dr. Rencang Li
Acknowledgement Dr. Mai Zhou Dr. Arne Bathke Dr. William Griffith Dr. William Rayens Dr. Rencang Li


