Elliptic Curve Cryptography Jen-Chang Liu 2004 Adapted from

Elliptic Curve Cryptography Jen-Chang Liu, 2004 Adapted from lecture slides by Lawrie Brown Ref: RSA Security’s Official Guide to Cryptography

No Singhalese(錫蘭人), whether man or woman, would venture out of the house without a bunch of keys in his hand, for without such a talisman(護身符) he would fear that some devil might take advantage of his weak state to slip into his body. —The Golden Bough, Sir James George Frazer

Review: Requirement for publickey cryptography n Diffie and Hellman (1976) proposed the public-key cryptography requirement: n n n It is computationally easy to generate a pair of keys (X) It is computationally easy for a sender to encrypt Y = EKU b It is computationally easy for a receiver to decrypt X = DKR (Y) b It is computationally infeasible for an opponent, knowing the public key, to determine the private key It is computationally infeasible for an opponent, knowing the public key and ciphtertext, to recover the plaintext => Trap-door one-way function

Review: one-way function n 1968, R. M. Needham’s system Encrypted password list A’s password n n … One-way cipher A’s encrypted password … 1974, G. Purdy published the first detail description of such a one-way function One-way function n Computation in Zp , Hard to invert!

Review: (trapdoor) one-way function Y=f(X): easy target domain X=f -1 (Y): infeasible ( > polynomial time) X=f. K-1 (Y): easy if trap-door K is known ( ~ polynomial time) The notion of “computationally infeasible” plays an important role A enciphering transformation that can safely be regarded as a (trapdoor) one-way function in 1994 might lose its one-way or trapdoor status in 2004 or 2994

Elliptic Curve Cryptography (ECC) n n majority of public-key crypto (RSA, D-H) use either integer or polynomial arithmetic with very large numbers/polynomials imposes a significant load in storing and processing keys and messages an alternative is to use elliptic curves offers same security with smaller bit sizes

Outline n n Operations over abelian groups (可換群) Elliptic curves over the reals Elliptic curves over the finite fields Elliptic curve cryptography

Abelian group n n Group with communicative property Group: {G, • } n n n G: a set of elements • : binary operation to each pair (a, b) in G obeys: n n closure: a • b is also in G associative law: (a • b) • c = a • (b • c) has identity e: e • a = a • e = a has inverses a-1: a • a-1 = e

Public ciphers based on an abelian group n Exponentiation (repeated multiplication) in RSA and D-H algorithm k times hard problem n n Idea: Find another abelian group! In elliptic curves, we define the addition operation such that it forms an abelian group k times

Classes of elliptic curves used by cryptographers

Outline n n Operations over abelian groups (可換群) Elliptic curves over the reals Elliptic curves over the finite fields Elliptic curve cryptography

Real Elliptic Curves n n n Elliptic curves are not ellipses an elliptic curve is defined by an equation in two variables x & y, with coefficients consider a cubic elliptic curve of form n n n y 2 = x 3 + ax + b where x, y, a, b are all real numbers also define O (point at infinity)

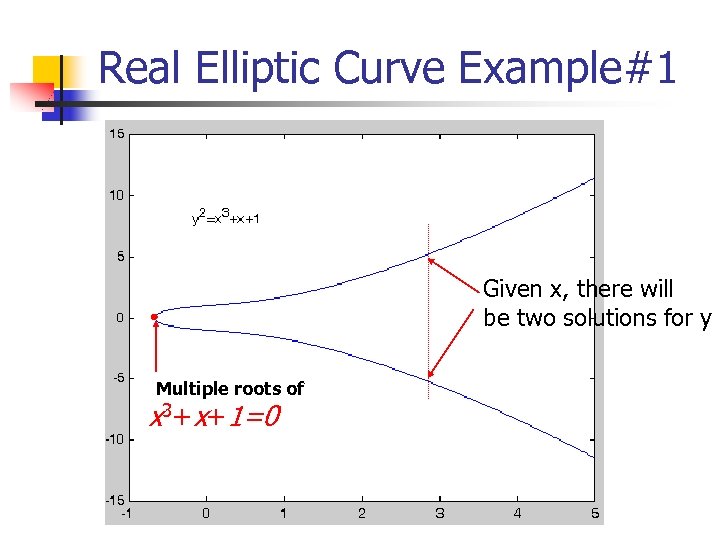Real Elliptic Curve Example#1 Given x, there will be two solutions for y Multiple roots of 3+ + x x 1=0

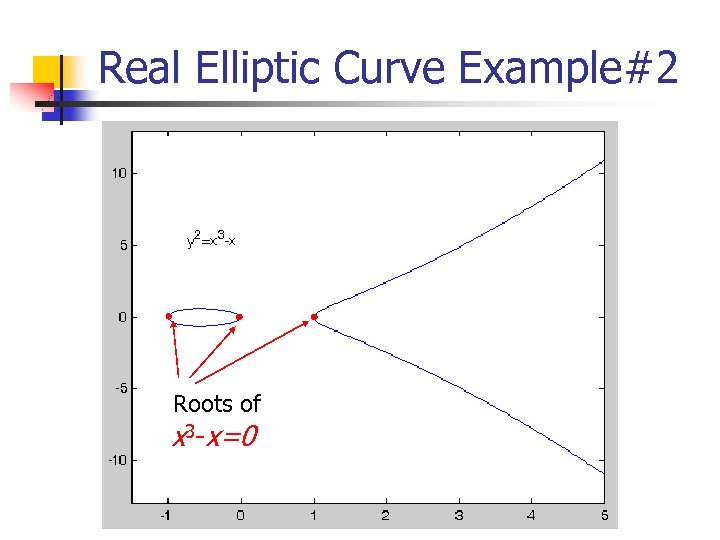Real Elliptic Curve Example#2 Roots of x 3 -x=0

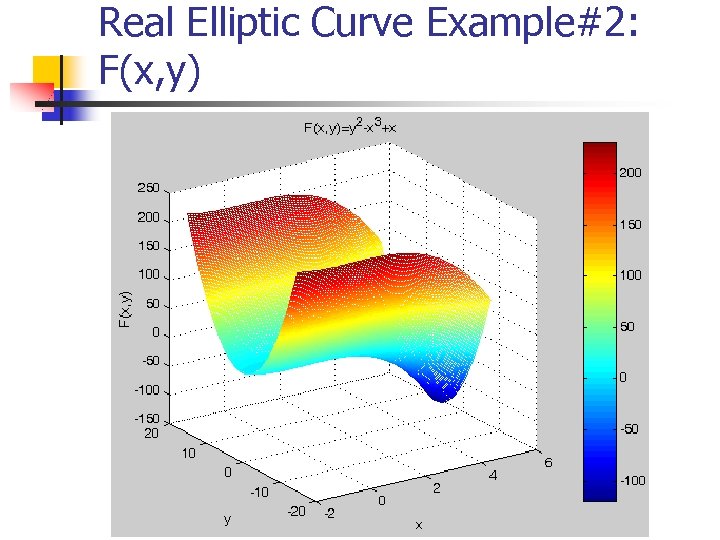Real Elliptic Curve Example#2: F(x, y)

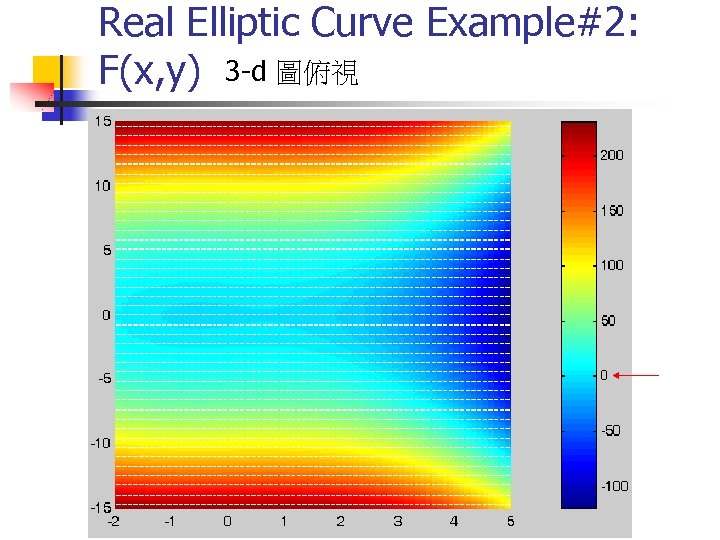Real Elliptic Curve Example#2: F(x, y) 3 -d 圖俯視

Addition over elliptic curve Definition: Let E be an elliptic curve over the real numbers. P and Q be two points on E. We define the negative of P and the sum P+Q as: 1. If P is the point at infinity O, then –P=O and P+Q = Q. [i. e. O servers as the identity (zero)] 2. P = (x, y), then –P=(x, -y) [-P must lie on elliptic curve] n

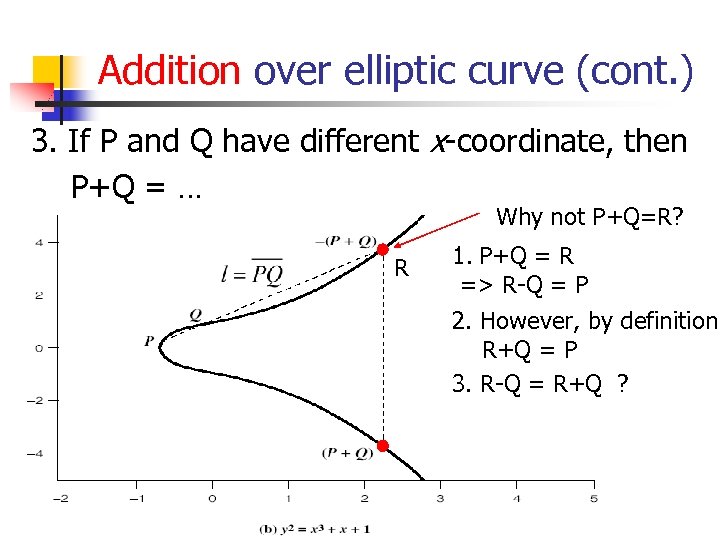Addition over elliptic curve (cont. ) 3. If P and Q have different x-coordinate, then P+Q = … Why not P+Q=R? R 1. P+Q = R => R-Q = P 2. However, by definition R+Q = P 3. R-Q = R+Q ?

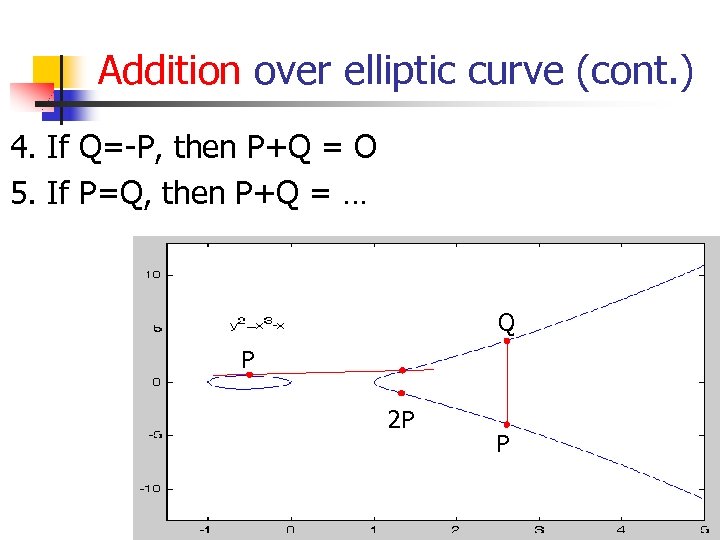Addition over elliptic curve (cont. ) 4. If Q=-P, then P+Q = O 5. If P=Q, then P+Q = … Q P 2 P P

Closure of addition operation Why there is exactly one point where the line intersects with elliptic curve? (P+Q 一定有定義? ) (x 3, ax 3+b) Case 1: P=Q n Line function: (x, ax+b) (x 2, y 2)= (x 1, y 1)= Solve

Closure of addition operation (cont. ) Solve => 三個根： (x 1, y 1), (x 2, y 2), (x 3, y 3) => => =>

Closure of addition operation (cont. ) n n n Case 2: P=Q Slope of the tangent line: Solution of P+Q:

Outline n n n Operations over abelian groups (可換群) Elliptic curves over the reals Elliptic curves over the finite fields n n n Over Zp Over GF(2 m) Elliptic curve cryptography

Finite Elliptic Curves n n Elliptic curve cryptography uses curves whose variables & coefficients are discrete and finite have two families commonly used: n prime curves Ep(a, b) defined over Zp n n n use integers modulo a prime best in software binary curves E 2 m(a, b) defined over GF(2 m) n n use polynomials with binary coefficients best in hardware

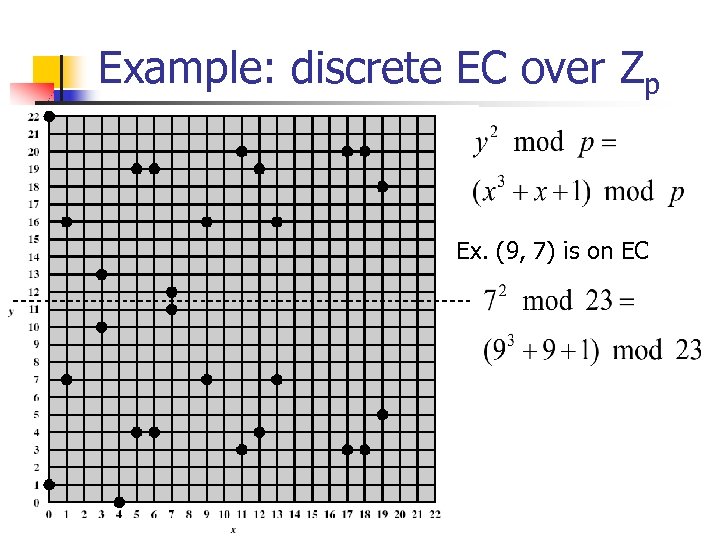Example: discrete EC over Zp Ex. (9, 7) is on EC

EC over Zp 1. P+O = P 2. If P=(xp, yp), then P+ (xp, -yp) = O 3. If P=(xp, yp), Q=(xq, yq), R=P+Q=(x. R, y. R) is where

EC over Zp (cont. ) 4. Scalar multiplication is defined as repeated addition. Ex. 4 P = P+P+P+P Q: How many points are defined on EC (given prime modulo p)? When p is large, it approximates the size of Zp

Outline n n Operations over abelian groups (可換群) Elliptic curves over the reals Elliptic curves over the finite fields Elliptic curve cryptography

Elliptic Curve Cryptography n n n ECC addition is analog of modulo multiply in RSA ECC repeated addition is analog of modulo exponentiation need “hard” problem equiv. to discrete log n n Q=k. P, where Q, P belong to a prime curve is “easy” to compute Q given k and P but “hard” to find k given Q, P known as the elliptic curve logarithm problem

EC discrete log problem n Certicom example: E 23(9, 17) n n n EC: P=(16, 5), Q=(4, 5), determine k s. t. Q=k. P Brute force method: P=(16, 5); 2 P=(20, 20); 3 P=(14, 14); 4 P=(19, 20) 5 P=(13, 10); 6 P=(7, 3); 7 P=(8, 7); 8 P=(12, 17); 9 P=(4, 5)

ECC Diffie-Hellman n n n can do key exchange analogous to D-H users select a suitable curve Ep(a, b) select base point G=(x 1, y 1) with n s. t. n. G=O A & B select private keys n. A

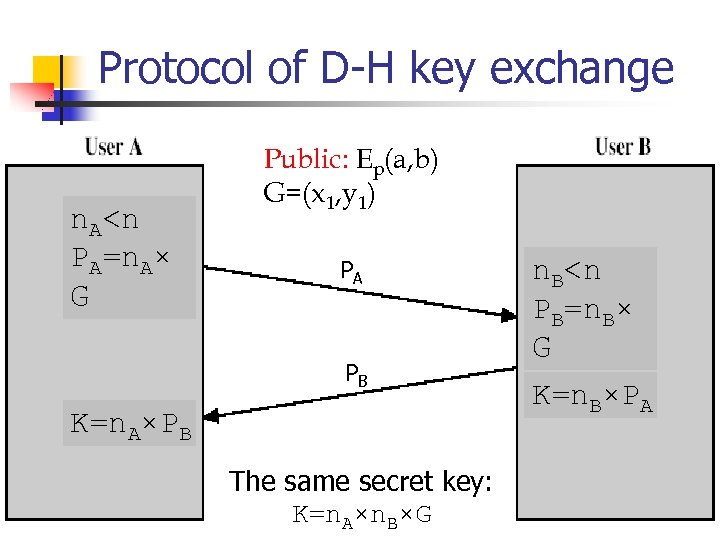Protocol of D-H key exchange n. A

ECC Encryption/Decryption n n several alternatives, will consider simplest must first encode any message M as a point on the elliptic curve Pm n n n Problem: not all discrete points are defined in EC select suitable curve & point G as in D-H each user chooses private key n. A

Example: ECC encryption n n EC curve on Zp : y 2 = x 3 -x + 188 G = (0, 376), p = 751 A’s public key PA = (201, 5) Plaintext Pm=(562, 201) B selects random k=386, then encryt Pm as Cm={k. G, Pm+k. PA} = {386(0, 376), (562, 201)+386(201, 5)} = {(676, 558), (385, 328)}

ECC Security n n compared to factoring, can use much smaller key sizes than with RSA etc for equivalent key lengths computations are roughly equivalent