Эллипс Выполнила Старикова Александра 10 А Эллипс

Эллипс Выполнила: Старикова Александра 10 «А»

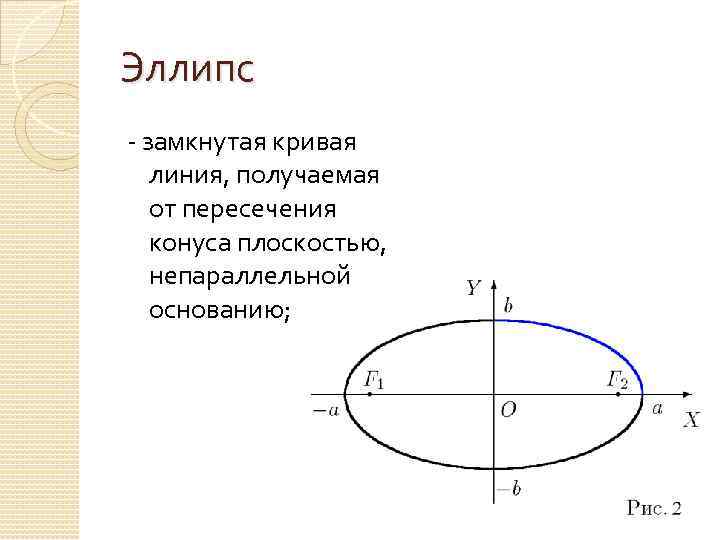Эллипс - замкнутая кривая линия, получаемая от пересечения конуса плоскостью, непараллельной основанию;

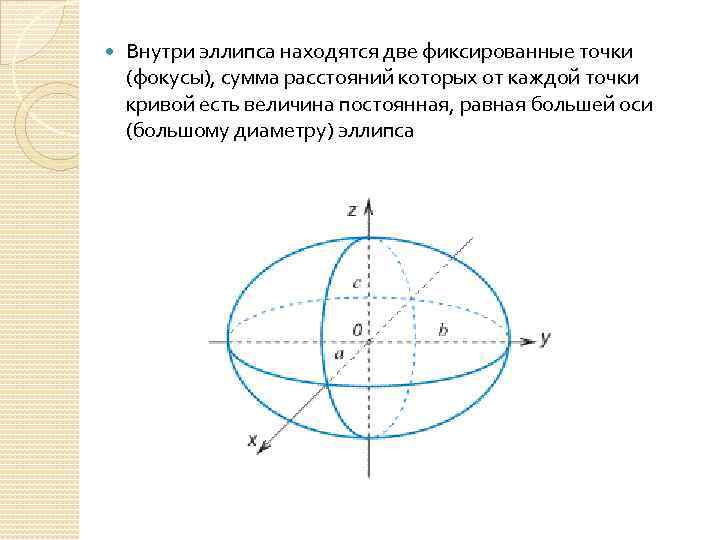Внутри эллипса находятся две фиксированные точки (фокусы), сумма расстояний которых от каждой точки кривой есть величина постоянная, равная большей оси (большому диаметру) эллипса

Чертеж эллипса F 1 , F 2 – фокусы. F 1 = ( c ; 0); F 2 (- c ; 0) с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.

Каноническое уравнение Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса): Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.

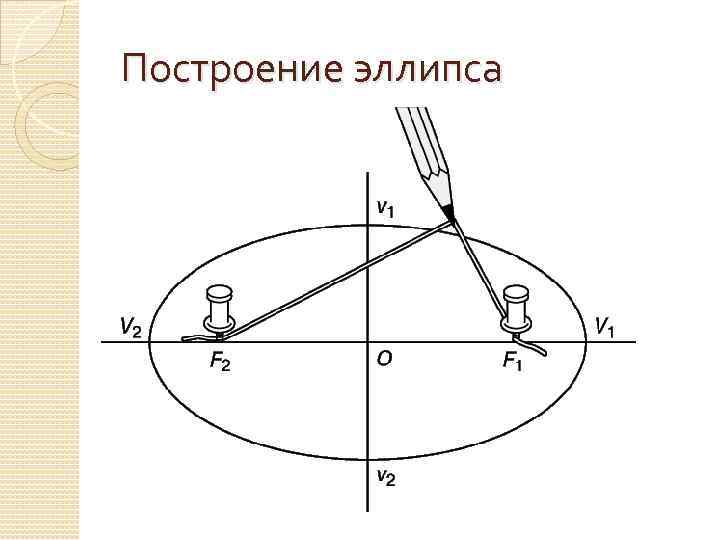Построение эллипса

Свойства эллипса Эллипс имеет центр симметрии (начало координат О) и две взаимно перпендикулярные оси симметрии (оси Ox и Oy ). Эти оси называются осями эллипса: та из них, на которой лежат фокусы, называется большой осью, а другая – малой осью; величины a и b называютсябольшой и малой полуосями Если и — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой равен углу между этой касательной и прямой

Свойства Эллипса Точки пересечения эллипса с осями являются его вершинами. Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы. В канонической для эллипса системе координат, все точки эллипса находятся в прямоугольнике или

Свойства эллипса Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе. Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся

Связанные определения Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2 a Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса. Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b. Точка пересечения большой и малой осей эллипса называется его центром. Расстояния и от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.

Отношение расстояния между фокусами к большой оси называется эксцентриситетом. Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут. Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью:

Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения или