Элементы зонной теории Уравнение Шредингера

Элементы зонной теории Уравнение Шредингера для кристалла • Ĥ - оператор Гамильтона твердого тела, • Е – полная энергия твердого тела, • - волновая функция - собственная функция оператора Ĥ, отвечающая собственному значению Е

Оператор Ĥ включает в себя: • кинетическую энергию всех электронов • кинетическую энергию всех ядер • энергию кулоновского отталкивания электронов • энергию кулоновского отталкивания ядер • энергию кулоновского притяжения электронов и ядер

Если кристалл находится во внешнем поле, то в гамильтониан надо добавить • потенциальную энергию всех частиц кристалла во внешнем поле • Гамильтониан кристалла во внешнем поле

Для решения уравнения Шредингера используются приближения. 1) Адиабатическое приближение Исходная задача разбивается на две Электронное уравнение Ядерное уравнение

2) Одноэлектронное приближение - многоэлектронная задача сводится к одноэлектронной. Потенциальную энергию кристалла представляют в аддитивном виде Гамильтониан НЭ принимает вид

Собственная функция гамильтониана НЭ представляется детерминантом Слэтера

Одноэлектронный потенциал V и волновые функции φi находятся из вариационного принципа – минимума полной энергии кристалла, рассматриваемой как функционал от функций φi δЕ=0 Это приводит к уравнению самосогласованного поля Хартри-Фока которое решается методом итераций.

Из уравнения Хартри-Фока следует, что одноэлектронный потенциал V равен Энергия εi равна энергии, необходимой для удаления из кристалла одного электрона , находящегося в i – ом состоянии теорема Купмэнса

Если усреднить обменный потенциал по всем электронам (локальное приближение Слэтера ), то этот потенциал становится одинаковым для всех электронов и уравнение Хартри-Фока принимает вид Полная энергия электронного гамильтониана равна

Потенциал V обладает трансляционной симметрией кристалла Благодаря этому волновая функция одноэлектронного уравнения Шредингера может быть представлена в в иде ( теорема Бло - периодическая функция. Следовательно, волновая функция электрона, движущегося в периодическом поле, представляет собой модулированную плоскую волну

• Вектор k называют квазиволновым вектором • p – вектор, имеющий размерность импульса. Он называется квазиимпульсом

Названия « квазиволновой вектор » и « квазиимпульс » указывают на аналогию между движением электрона в кристалле и вакууме. С ходств о и различи е между импульсом и квазиимпульсом: • импульс характеризует движение свободного электрона в вакууме , облада ющего инвариантностью относительно сдвига на любой вектор (все точки пространства эквивалентны); • квази импульс характеризует движение в периодическом силовом поле кристалла , облада ющего инвариантностью относительно сдвиг ов на векторы прямой решетки.

Свойства одноэлектронных энергий и волновых функций • Энергии и волновые функции являются периодическими функциями волнового вектора • Электронные состояния, волновые векторы которых отличаются на вектор обратной решетки описывают физически эквивалентные состояния. • Неэквивалентным , физически отличным электронным состояниям отвечают волновые векторы, находящиеся в первой зоне Бриллюэна.

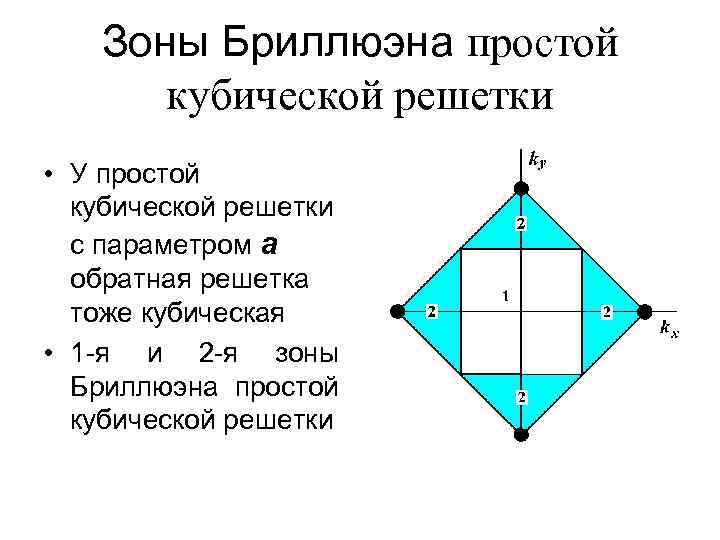
Зоны Бриллюэна простой кубической решетки • У простой кубической решетки с параметром а обратная решетка тоже кубическая • 1 -я и 2 -я зоны Бриллюэна простой кубической решетки

Периодические граничные условия Борна- Кармана • Для решения дифференциального уравнения Шредингера необходимо задать граничные условия на поверхности кристалла. • Учесть реальную поверхность кристалла сложно. • Однако, объемные электронные свойства кристаллов относительно слабо зависят от поверхности. • Поэтому можно заменить реальную поверхность модельной.

• В методе Борна-Кармана кристалл разбивается на большие , одинаковые блоки. Считается, что электронные свойства этих блоков одинаковы. • Блоки представляют собой увеличенные элементарные ячейки. Ребра блоков даются векторами • Волновые функции в блоках полагаются одинаковыми

• Чтобы волновой вектор находился в пределах 1 -ой зоны Бриллюэна надо ограничить изменение целых чисел • Поэтому общее число разных значений квазиволнового вектора равно N = N 1 · N 3 - 2 числу элементарных ячеек в блоке периодичности кристалла.

Методы расчета энергетического спектра в кристаллах • Для решения одноэлектронного уравнения Шредингера применяют различные методы : • 1) первопринципные методы , в которых используются только фундаментальные параметры атомов. Основаны на методе Хартри-Фока или методе функционала электронной плотности. В зависимости от вида базисных функций различают : • метод ортогонализованных плоских волн (ОПВ) • метод присоединенных плоских волн (ППВ) • метод линейных комбинаций атомных орбиталей (ЛКАО) • метод псевдопотенциала • метод функций Грина

• 2) эмпирические методы , в которых для получения согласия теории с экспериментом параметры теоретического метода определяются с использованием экспериментальных данных. К этим методам относятся : • метод сильной связи • метод эмпирического псевдопотенциала • 3) ( kp ) метод - интерполяционный метод, в котором на основе данных о зонном спектре в экстремумах определяются зонные состояния в окрестности этих экстремумов • 4) модельные методы – метод Кроннига-

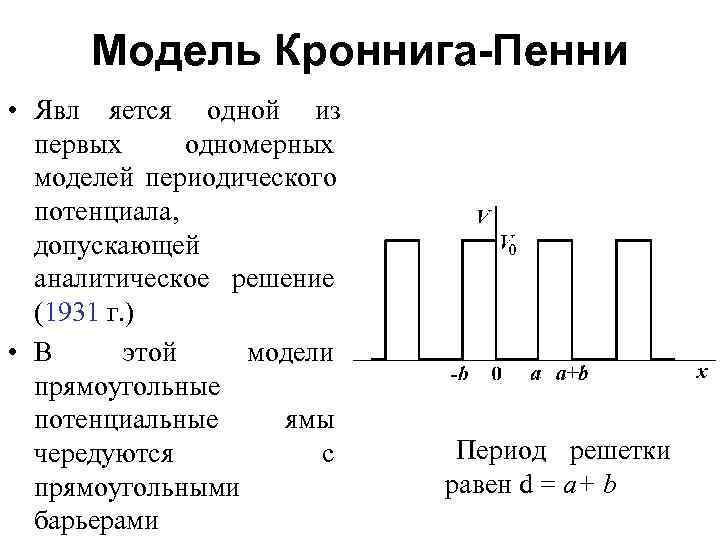
Модель Кроннига-Пенни • Явл яется одной из первых одномерных моделей периодического потенциала, допускающей аналитическое решение (1931 г. ) • В этой модели прямоугольные потенциальные ямы чередуются с Период решетки прямоугольными равен d = а+ b барьерами

Из решения уравнения Шредингера находятся стационарные состояния электрона в кристалле. Общие решения уравнения Шредингера в барьере (1) и яме (2) имеют вид

Волновая функция и ее первая производная должны быть непрерывны на границах барьеров и ям, кроме того волновая функция должна удовлетворять теореме Блоха k – волновое число одномерного кристалла

Подставляя волновые функции в условия сшивания, получаем систему уравнений для определения коэффициентов разложения А 1 , А 2 В 1 , , В 2

Условием ее разрешимости является равенство нулю детерминанта. Это приводит к уравнению (при Е < V 0) которое дает закон дисперсии – зависимость энергии электрона от волнового числа Е(k). Решается численным путем.

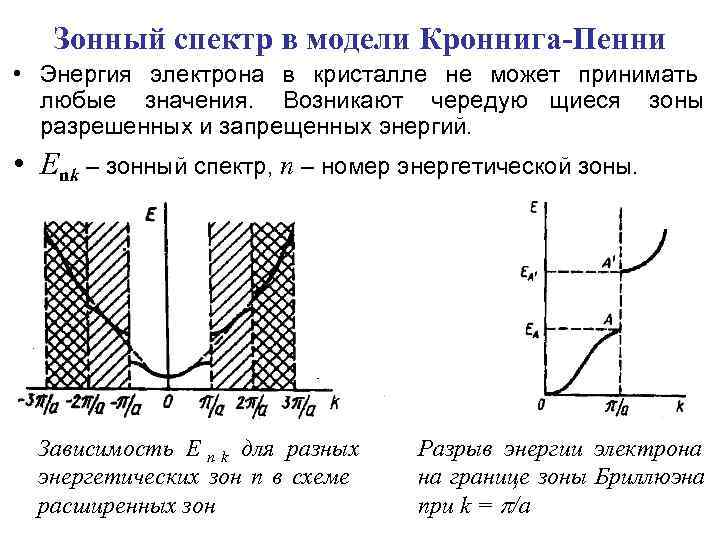
Зонный спектр в модели Кроннига-Пенни • Энергия электрона в кристалле не может принимать любые значения. Возникают чередую щиеся зоны разрешенных и запрещенных энергий. • Enk – зонный спектр, n – номер энергетической зоны. Зависимость E n k для разных Разрыв энергии электрона энергетических зон n в схеме на границе зоны Бриллюэна расширенных зон при k = /a

Установим связь зонных энергий электрона в кристалле с уровнями изолированной квантовой ямы. Для этого устремим ширину барьера b и высоту барьера V 0 к бесконечности, тогда Поскольку левая часть уравнения всегда имеет конечное значение, то решение возможно лишь когда

Или Откуда в пределе получаем уровни энергии электрона в изолированной яме бесконечной глубины и ширины а

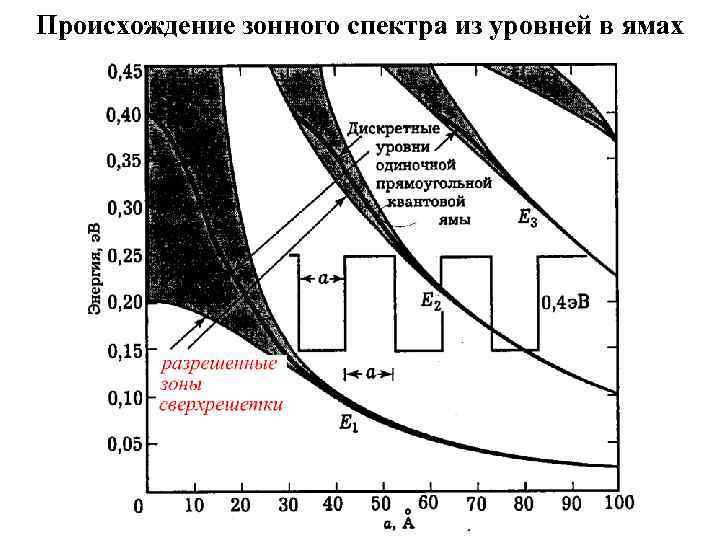
Происхождение зонного спектра из уровней в ямах

Образование зонного спектра кристалла из уровней атомов в методе сильной связи Энергетические уровни электронов в изолированном атоме расщепляются в энергетическую зону при образовании из этих атомов кристаллической решетки. a - постоянная решетки

Металлы, диэлектрики, полупроводники • Каждая разрешенная зона с номером n содержит число энергетических уровней N , равно е числу значений волнового вектора в 1 -ой зоне Бриллюэна. • Согласно принципу Паули на каждом уровне могут находиться два электрона с противоположно направленными спинами. Поэтому в одной энергетической зоне можно разместить 2 N электронов. • Если в элементарной ячейке кристалла имеется р электронов, то в блоке периодичности их будет p. N. • Поэтому число заполненных зон равно p. N/2 N = p/2. • С лед овательно , если число р – четное, то кристалл –

• Na = [1 s 22 p 6]3 s 1 – металл, верхняя валентная зона заполнена на половину • Mg = 1 s 22 p 63 s 2 - пример исключения, является металлом, потому что 3 s - валентная зона перекрывается с верхней пустой зоной, образованной из 3 р - уровней • Na. Сl : Na+ = 1 s 22 p 6, Сl- = 1 s 22 p 63 s 23 p 6 диэлектрик, Eg 10 э. В

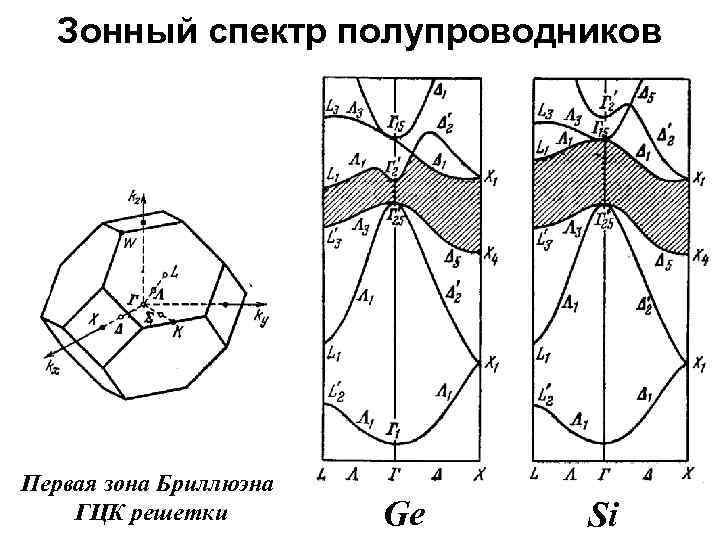
Зонный спектр полупроводников Первая зона Бриллюэна ГЦК решетки Ge Si