Элементы технической теории пологих оболочек
x z f b y a Оболочка называется пологой, если f/b < 1/5, где a > b Геометрия пологой оболочки близка к геометрии Эвклида на плоскости ее проекции. Вместо выражения можно записать и считать В исходных уравнениях Гауссова кривизна поверхности Уравнение поверхности переноса Поверхность – эллиптический параболоид
Основные уравнения теории пологих оболочек 1. Уравнения равновесия 2. Геометрические уравнения 3. Физические уравнения
Вывод уравнения неразрывности деформаций
Вводим функцию напряжений При по формулам уравнения равновесия принимают вид Принимая во внимание, что Получим уравнение равновесия - оператор Власова
Уравнения для пологих оболочек в смешанной форме Постановка задачи: решить систему с заданными граничными условиями В каждой точке контура надо сформулировать четыре граничных условия, два из них выразить через прогиб, а два других выразить через функцию напряжений.
Расчет пологих оболочек, опертых по контуру на диафрагмы, на действие поперечной нагрузки x z f Оболочка – эллиптический параболоид b y a Постановка задачи Система уравнений Граничные условия
Решение в двойных тригонометрических рядах обозначим В соответствии с принципом суперпозиции имеем нагрузку Прогиб оболочки и функцию напряжений ищем в виде
Подставляем в уравнение равновесия Получаем алгебраическое уравнение Подставляем деформаций в уравнение неразрывности Получаем алгебраическое уравнение
Расчет оболочки сводится к решению системы алгебраических уравнений
В соответствии с принципом суперпозиции имеем Предварительно вычисляем элементы матриц
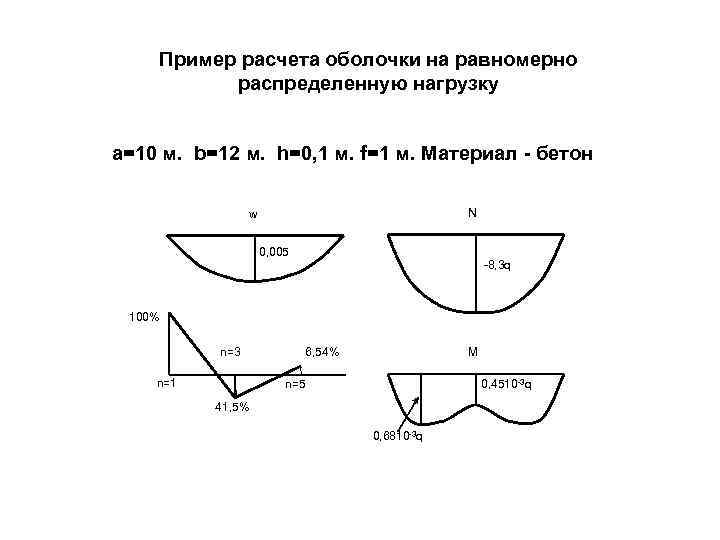
Пример расчета оболочки на равномерно распределенную нагрузку а=10 м. b=12 м. h=0, 1 м. f=1 м. Материал - бетон N w 0, 005 -8, 3 q 100% n=1 M 6, 54% n=3 0, 4510 -3 q n=5 41, 5% 0, 6810 -3 q
Скачать презентацию Элементы технической теории пологих оболочек x z
Элементы технической теории пологих оболочек.ppt