Элементы теории вероятности Литература 1 2 3

Элементы теории вероятности

Литература 1. 2. 3. 4. 5. Денисова Л. В. , Хмельницкая Е. В. , Харченко Л. А. Измерения и методы математической статистики в физическом воспитании и спорте. – К. : Олимп л-ра, 2008. – 127 с. Лакин Г. Ф. Биометрия : Учеб. пособие для унив-в и педаг. ин-в. - М. : Высш. шк. , 1973. – 343 с. Містулова Т. Є. Математичні методи в теорії та практиці спорту. К. : Науковий світ, 2004. – 90 с. Основы математической статистики: Учеб. пособие/ Под общ. ред. В. С. Иванова - М. : Физкультура и спорт, 1990. - 176 с. Начинская С. В. Основы спортивной статистики. – К. : Вища шк. , 1987. -189 с.

ПЛАН 1. Некоторые математические понятия и символы 2. Теория вероятности, вероятность, ее свойства 3. Случайная величина

1. МНОЖЕСТВО Х = х1, х2, х3, . . . хn хі – (“икс итое”) – любой из элементов множества, где і = 1, 2, 3, . . . n xn – (“икс энное”) – последний элемент множества, где n – количество элементов в множестве

2. СУММА хі 5. АБСОЛЮТНАЯ ВЕЛИЧИНА Ia. I =a I-a. I=a 6. УРАВНЕНИЕ S = V*t; Y = X 2+2 X+5

История возникновения теории вероятностей уходит в глубь веков, но математическое обоснование появилось только в середине 17 века. В это время во Франции при дворе были необыкновенно популярны азартные игры (от арабского «аз-захр» — игральная кость, испанского «azar» — игра в кости и французского «hasard» — случай, риск) Существует интересная легенда о причинах побудивших известного французского математика, философа, изобретателя Блеза Паскаля заняться проблемой выигрыша в кости В 1654 году, в переписке Блеза Паскаля с известным юристом и знаменитым математиком Пьером де Ферма, на примерах из разных азартных игр закладываются основы теории вероятностей

В 1657 году голландский математик, физик, астроном и изобретатель Христиан Гюйгенс (1629 — 1695) написал приложение «О расчётах в азартной игре» к книге его учителя ван Схоотена «Математические этюды» . Это было содержательное изложение начал зарождающейся тогда теории вероятностей. Гюйгенс, наряду с Ферма и Паскалем, заложил её основы. По этой книге знакомился с теорией вероятностей знаменитый швейцарский математик Якоб Бернулли, который и завершил создание основ теории Якоб Бернулли (1654 — 1705) ввёл значительную часть современных понятий теории вероятностей и сформулировал первый вариант закона больших чисел. Он подготовил монографию в этой области, однако издать её не успел. Она была напечатана посмертно, в 1713 году, его братом Николаем, под названием «Искусство предположений» . Это содержательный трактат по теории вероятностей, статистике и их практическому применении, итог комбинаторики и теории вероятностей XVII века. Имя Якоба носит важное в комбинаторике распределение Бернулли

Впервые основы теории вероятностей были последовательно изложены французским математиком и астроном Пьер-Симоном Лапласом (1749 – 1827) в книге «Аналитическая теория вероятностей» . В предисловии автор писал: «Замечательно, что наука, которая началась с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания. Ведь по большей части, важнейшие жизненные, вопросы являются на самом деле лишь задачами из теории вероятностей» Карл Фри дрих Гаусс ( 1777 — 1855) — выдающийся немецкий математик, астроном и физик, считается одним из величайших математиков всех времён. Гаусс создал «метод наименьших квадратов» (независимо открытый Лежандром) и начал исследования в области «нормального распределения ошибок» Абрахам де Муавр (1667 — 1754) — английский математик французского происхождения Доказал частный случаи теоремы Лапласа. Провёл вероятностное исследование азартных игр и ряда статистических данных по народонаселению. Кроме нормального, он использовал равномерное распределение. Для дискретного случая использовал и глубоко исследовал последовательности, названные им рекуррентными (возвратными) Симеон-Дени Пуассон (1781 — 1840) — знаменитый французский физик-математик. Он доказал частный случай больших чисел закона и одну из предельных теорем (теорема Пуассона, распределение Пуассона)

Пафну тий Львович Чебышёв (14 (26 мая) 1821 26 ноября (8 Марков, Андрей Андреевич (14 июня 1856 – 20 июля 1922) декабря) 1894) Александр Михайлович Ляпунов (1857— 1918) В конце ІХХ века теорию вероятности стали называть русской наукой Андрей Николаевич Колмогоров (1903— 1987) — выдающийся русский советский математик, основоположник современной теории вероятностей

Объектом исследования теории вероятности является случайное событие

СОБЫТИЯ § ДОСТОВЕРНОЕ – Е § НЕВОЗМОЖНОЕ – О § СЛУЧАЙНОЕ – A, B, C… P(A) – ВЕРОЯТНОСТЬ СОБЫТИЯ А

Теория вероятности – строгая математическая дисциплина, которая занимается поиском закономерностей случайный событий и изучает их

Вероятностью случайного события А называется число, которое характеризует возможность появления случайного события в конкретном испытании Обозначается – P(A) Читается– ВЕРОЯТНОСТЬ СОБЫТИЯ А

ПРИМЕР Е 1 = 2 белых кубика Е 2 = 5 зеленых кубиков Е 3 = 3 синих кубика Е 2+Е 3 = 5+3=8 – цветных кубиков Р(А) = = 0, 8 или 80%

- благоприятные исходы испытания - все элементарные, равновозможные исходы испытания

Свойства вероятности § если Р(А) = 1 – событие А достоверное § если Р(А) = 0 – событие А невозможное § если 0 < Р(А) <1 – событие А случайное

Величину называют случайной, если в результате испытания она принимает только одно какое-то значение, заранее неизвестное и зависящее от случайных причин § Дискретные (принимают конкретные значения с определенной вероятностью) § Непрерывные (которые принимают все значения из какого-то диапазона)

Эмпирические распределения

1. Математическая статистика и предмет ее изучения 2. Вариационный ряд и его графическая интерпретация 3. Метод средних величин 4. Генеральная и выборочная совокупности. Способы организации выборки 5. Выборочный метод. Доверительный интервал

Математическая статистика – раздел математики, который посвящен методам сбора, анализа статистических данных, а также обработки их в соответствии з законами теории вероятности.

Предметом изучения математической статистики (как и теории вероятности) является случайное событие

Группа чисел, относящихся к одному и тому же признаку, называется статистической совокупностью Каждый элемент совокупности называется вариантой – Хi Количество повторений вариант в совокупности называется частотой – ni Количество элементов в совокупности (сумма частот) называется объемом совокупности – n

1. Ранжирование – запись данных в порядке возрастание или убывания 2. Запись данных в виде вариационного ряда. Это двойной числовой ряд, где в один столбец (строку) записываются варианты, а в другой столбец (строку) их частоты соответственно. Вариационные ряды бывают: - интервальными - безинтервальными

У спортсменов зарегистрировано время восстановления пульса после прохождения дистанции (с): 81, 78, 84, 90, 78, 81, 74, 90, 74, 81, 84, 81, 90, 81 Объем совокупности – n = 14

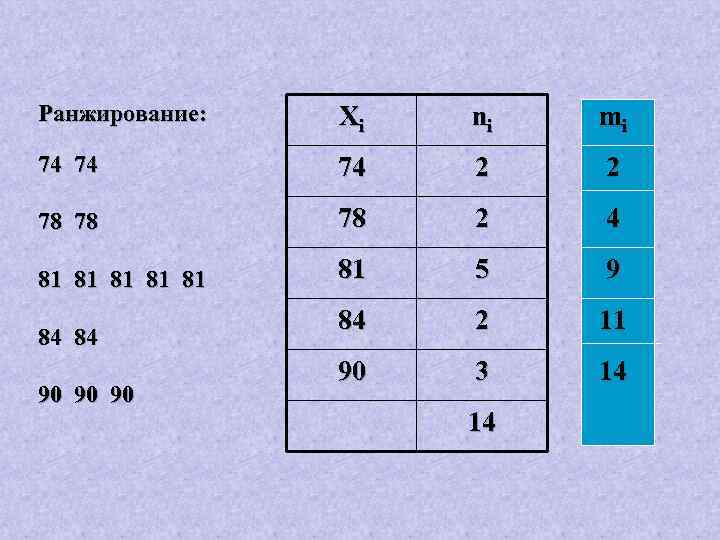Ранжирование: Xi ni mi 74 74 74 2 2 78 78 78 2 4 81 81 81 5 9 84 2 11 90 3 14 84 84 90 90 90 14

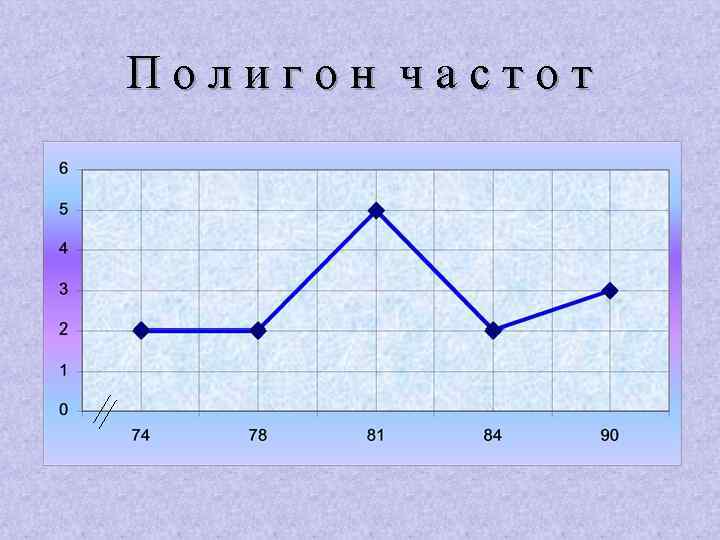Полигон частот

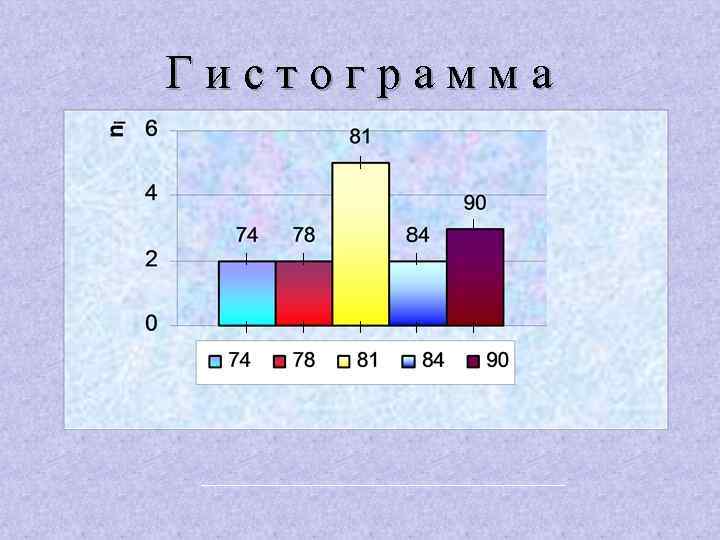Гистограмма

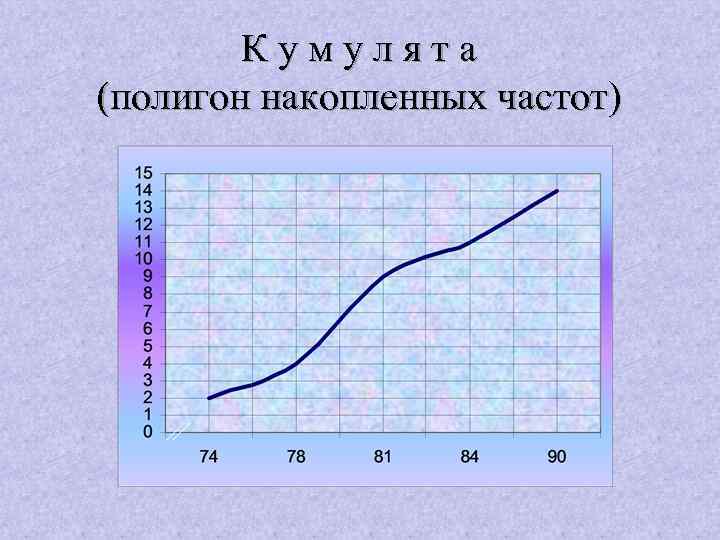Кумулята (полигон накопленных частот)

Характеристики (параметры) вариационного ряда Среднее арифметическое – такое значение признака, сумма отклонений от которого всех остальных значений равна нулю с учетом знака отклонения

Мода – вариант, который имеет наибольшую частоту, т. е. чаще всего встречается в нашей совокупности Медиана – вариант, который делит вариационный ряд пополам, т. е. соответствует средней частоте Если мода и медиана равны или близки по значению среднему арифметическому, то группу данных можно считать однородной

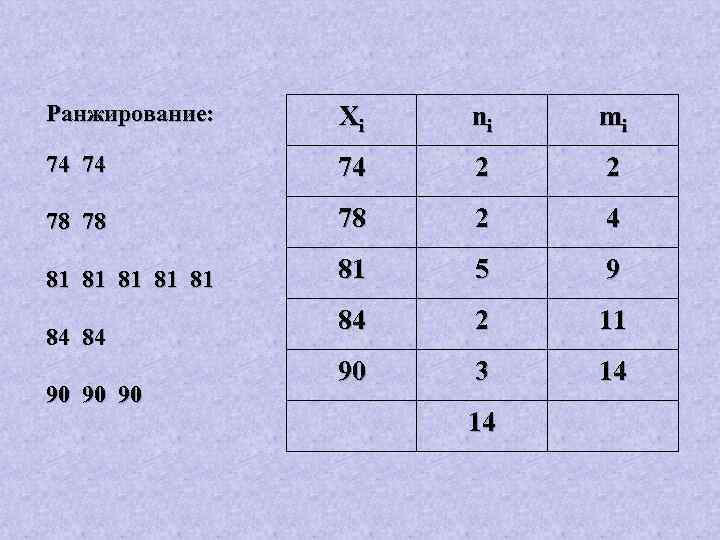Ранжирование: Xi ni mi 74 74 74 2 2 78 78 78 2 4 81 81 81 5 9 84 2 11 90 3 14 84 84 90 90 90 14

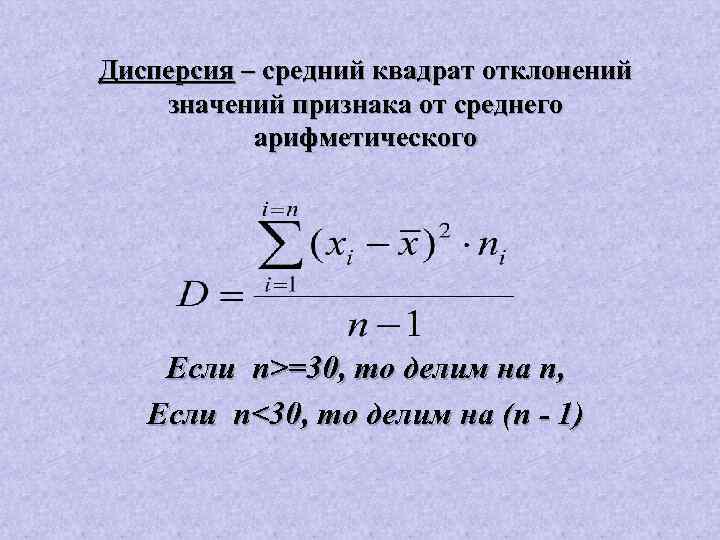Дисперсия – средний квадрат отклонений значений признака от среднего арифметического Если n>=30, то делим на n, Если n<30, то делим на (n - 1)

Среднее квадратическое отклонение (стандартное отклонение) Дисперсия и стандартное отклонение показывают рассеивание эмпирических данных вокруг среднего арифметического

Коэффициент вариации – показывает какую часть среднее квадратическое отклонение (рассеивание) составляет от среднего арифметического в процентах Если V <= 10% - статистическую совокупность можно считать однородной Если V > 10% - статистическую совокупность считают неоднородной

Метод средних величин позволяет производить анализ и разделение с помощью характеристик вариационных рядов, а также решать задачи на нормирование и сравнение признаков