Элементы теории вероятностей Составитель доцент кафедры ИТОи

Элементы теории вероятностей © Составитель: доцент кафедры ИТОи. М КГПУ им. В. П. Астафьева Романова Н. Ю.

Одни из ключевых понятий - ИСПЫТАНИЕ (опыт) и ИСХОД (элементарный исход)

Испытанием называется эксперимент с очерченным набором возможных взаимоисключающих результатов. Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Эксперимент должен быть повторяемым Если есть эксперимент, есть и возможные результаты. Эти результаты называются исходами. Два исхода никогда не могут случиться одновременно. Реализация того или иного исхода - случайное событие.

Совокупность всех элементарных исходов эксперимента носит название «множество (или пространство) всех элементарных исходов случайного эксперимента» . Обозначение: Ω = { ω1, ω2, … , ωn}

Примеры Традиционные: Монетки, Кубики, Шарики, Детали, Игральные карты и т. д. Пример 1. перечислить все возможные исходы при подбрасывании 2 -х монет: ОР, РО, РР, ОО. Те элементарные исходы, при которых реализуется событие А, называются элементарными исходами, благоприятствующими наступлению событию А, или просто благоприятными исходами. Пример 2. Бросаем кость два раза. Надо выписать все элементарные исходы, при которых сумма выпавших очков равна четырем (событие А - сумма очков равна 4): равна четырем (событие А - сумма очков равна 4) ω1 = {3; 1}, ω2 = {1; 3}, ω3 = {2; 2}.

Для определения количества исходов (всех исходов и исходов, отвечающих определенным требованиям) помогает наука КОМБИНАТОРИКА

Комбинаторика - наука о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Правило произведения Если объект A можно выбрать m способами, а другой объект B можно выбрать n способами, тогда пару (объект А, объект В) можно выбрать m∙n способами. Аналог в теории множеств: количество элементов декартова произведения множеств равно произведению количеств элементов "умножаемых" множеств. Правило легко обобщается на несколько типов объектов.

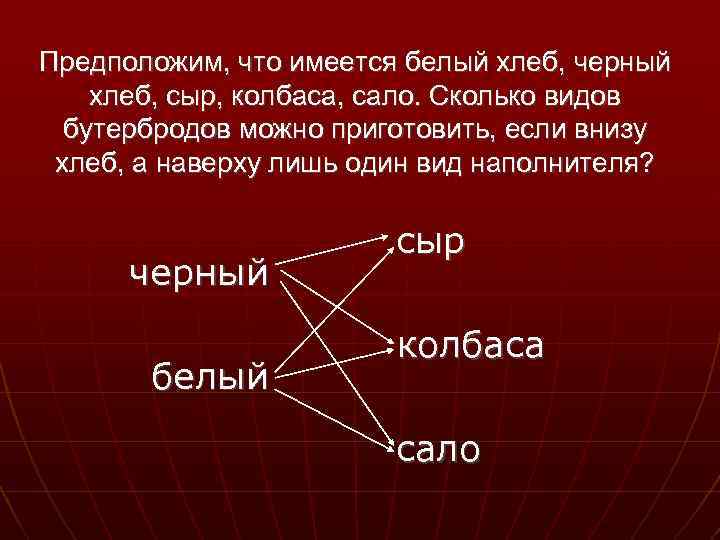Предположим, что имеется белый хлеб, черный хлеб, сыр, колбаса, сало. Сколько видов бутербродов можно приготовить, если внизу хлеб, а наверху лишь один вид наполнителя? черный белый сыр колбаса сало

Отличающиеся друг от друга порядком наборы, составленные из всех элементов данного конечного множества, называются перестановками этого множества. Число всех перестановок множества из n элементов обозначается Pn и определяется по формуле: Упорядоченные наборы, состоящие из k различных элементов, выбранных из данных n элементов, называются размещениями из n элементов по k. Число всех размещений из n элементов по k обозначается Ank и определяется по формуле Неупорядоченные наборы, состоящие из k элементов, взятых из данных n элементов, называются сочетаниями из n элементов по k. Число сочетаний из n элементов по k обозначается Cnk и определяется по формуле

В основе теории вероятностей лежит понятие случайного события. Случайным называется событие, которое в данном опыте может произойти, а может и не произойти.

События зачастую обозначаются латинскими буквами – А, В, С. . . Событие называют достоверным в данном опыте, если оно обязательно произойдет в этом опыте ( ). Событие называется невозможным в данном опыте, если оно в этом опыте произойти не может (Ø).

Два события называются совместными в данном опыте, если появление одного из них не исключает появления другого в этом опыте, и несовместными, если они не могут произойти вместе при одном и том же испытании. ! Несколько случайных несовместных событий образуют полную группу, если в результате испытания появится только одно из них. Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Отдельно для произвольного события A выделяют событие A, которое читается как «не A» и означает, что событие A не произошло.

Суммой или объединением двух событий называется событие, состоящее в появлении хотя бы одного из них. Сумма двух событий A и В обозначается А+В (ИЛИ) Произведением или пересечением двух событий называется событие, состоящее в одновременном их появлении. Произведение двух событий A и B обозначается А В (И)

Разностью событий A и В называется событие, которое означает, что наступает событие A и не происходит событие B. Разность событий принято обозначать А-В (или АВ)

Вероятность события

Основной числовой характеристикой случайного события является его вероятность как мера его объективной возможности. Классическое определение вероятности. Вероятность события A определяется формулой где n — число всех исходов опыта, m- число исходов, благоприятствующих событию A.

Статистическое определение вероятности. Относительная частота события A (или просто частота) определяется формулой где m — число опытов, в которых появилось событие , n — число всех проведенных опытов. Вероятностью события называют число, около которого группируются значения относительной частоты данного события в различных сериях большого числа испытаний.

Или от 0 до 100%

Свойства вероятностей: вероятность достоверного события равна единице; вероятность невозможного события равна нулю; вероятность случайного события A выражается положительным числом, меньшим единицы: для любых событий A и B (формула сложения вероятностей) вероятность события противоположного A:

Условная вероятность Вероятность события A при условии, что произошло событие B, называется условной вероятностью и обозначается

Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место: В качестве важного следствия этой теоремы следует отметить, что вероятность произведения независимых событий равна произведению вероятностей этих событий

Определения гипотез ( Обозначения: H 0, H 1, H 2…) Гипотеза - научное предположение, выдвигаемое для объяснения некоторого явления и требующее верификации. Конкурирующая гипотеза альтернативное объяснение результатов исследования, которое с логической точки зрения не может быть верным, если верна исходная гипотеза.

Формула полной вероятности. Следствием обоих основных теорем – теоремы сложения вероятностей и теоремы умножения вероятностей– является так называемая формула полной вероятности. Пусть имеется полная группа несовместных событий , называемых также гипотезами. Тогда вероятность некоего события A, которое может произойти с этими гипотезами, равна:

Формула Байеса Одно из интересных применений формулы полной вероятности связано с формулами Байеса. Если в выражении для условной вероятности заменить вероятность по формуле полной вероятности, то получим формулу Байеса Это выражение применяется для вычисления условной вероятности гипотезы Н 1 после испытания, при котором произошло событие A. Другими словами, формулы Байеса позволяют переоценить вероятности гипотез, принятые до испытания (арпиорные), по результатам уже произведенного испытания.

Законы распределения случайных величин.

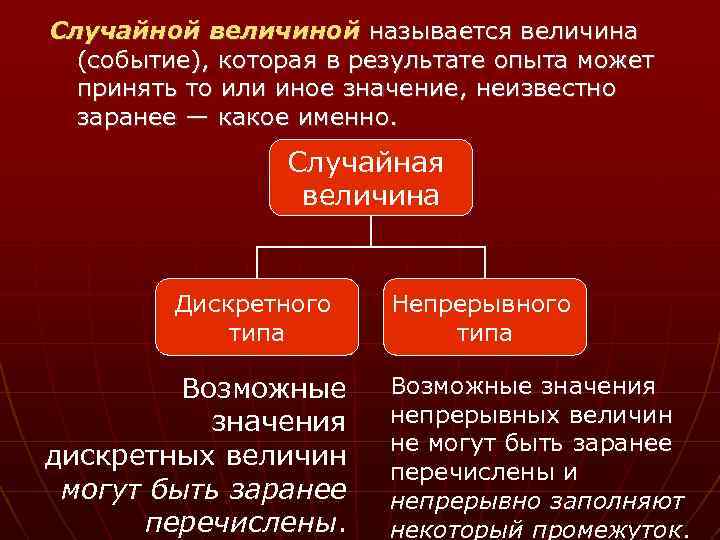Случайной величиной называется величина (событие), которая в результате опыта может принять то или иное значение, неизвестно заранее — какое именно. Случайная величина Дискретного типа Возможные значения дискретных величин могут быть заранее перечислены. Непрерывного типа Возможные значения непрерывных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.

Законы распределения дискретных случайных величин

Законом распределения дискретной случайной величины X называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины (x 1, x 2, …xn) и соответствующими им вероятностями (p 1, p 2, …pn). При этом: Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:

Геометрическое распределение Данное распределение соответствует задачам следующего вида: производится ряд независимых опытов, которые продолжаются до первого появления события A. Случайная величина — число проведенных опытов. При этом считается, что вероятность появления события A в одном опыте равна p. Тогда закон распределения вероятностей описывается следующей формулой:

Биномиальное распределение Пусть производится n последовательных независимых одинаковых испытаний, в каждом из которых может наступить или не наступить событие A. Вероятность наступления события A в каждом испытании p, а события A q=1 -p. Такая постановка эксперимента носит название «схема Бернулли» . Обозначим Pn(m) =P(событие A наступило m раз в n испытаниях). Тогда где Cnm — число сочетаний по m элементов из n, или биномиальный коэффициент.

Распределение Пуассона Говорят, что случайная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой где — некоторая положительная величина, называемая параметром закона Пуассона. Распределение Пуассона возникает там, где какие-либо точки (или другие элементы, например события во времени) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек (элементов), попавших в какую-то область. При этом должны выполняться следующие условия: точки (элементы) распределены в поле статистически равномерно со средней плотностью (при этом D, где D— элемент «пространства» , в котором происходят измерения, например, длина отрезка, элемент объема, промежуток времени и т. п. ); точки (элементы) попадают в неперекрывающиеся области независимым образом; точки появляются поодиночке (т. е. вероятность появления двух точек и больше в одном месте равна нулю).

Законы распределения непрерывных случайных величин

Закон распределения непрерывной величины должен позволять находить вероятность попадания ее значения в любой интервал (x 1, x 2), лежащий внутри отрезка, который заполняют все возможные значения X. Будем обозначать эту вероятность через Она быть представлена в виде интеграла от некоторой функции p(x)— плотности распределения вероятностей. При этом функция должна быть нормирована условием

Следует подчеркнуть, что для непрерывной случайной величины имеет смысл рассматривать только такое событие, как попадание в интервал, а не попадание в отдельную точку. Так как вероятность попадания непрерывной случайной величины в любую заранее заданную точку равна нулю.

Примерами распределений непрерывных случайных величин могут служить: равномерное распределение показательное распределение нормальное распределение и др.

Нормальный закон распределения

Предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях является Нормальный закон распределения (часто называемый законом Гаусса). К области применимости этого закона относятся такие случайные величины, как ошибки измерений, отклонение величин от среднего и т. д. , связанные с распределением сумм большого числа случайных величин.

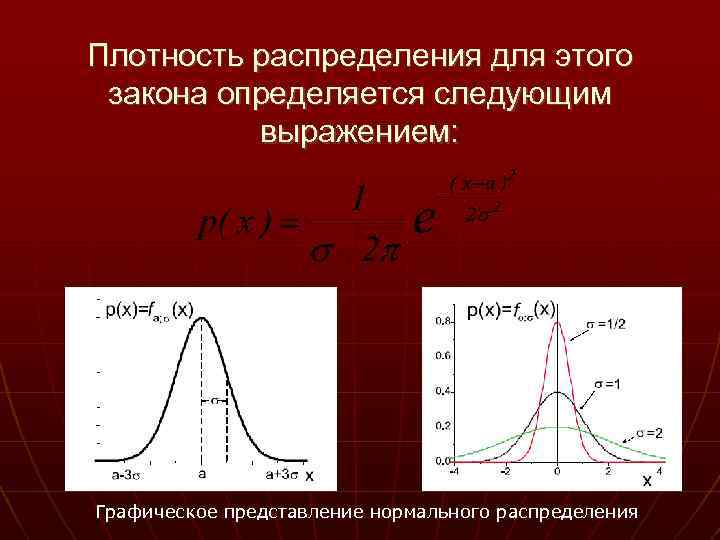Плотность распределения для этого закона определяется следующим выражением: Графическое представление нормального распределения

Нормальный закон распределения

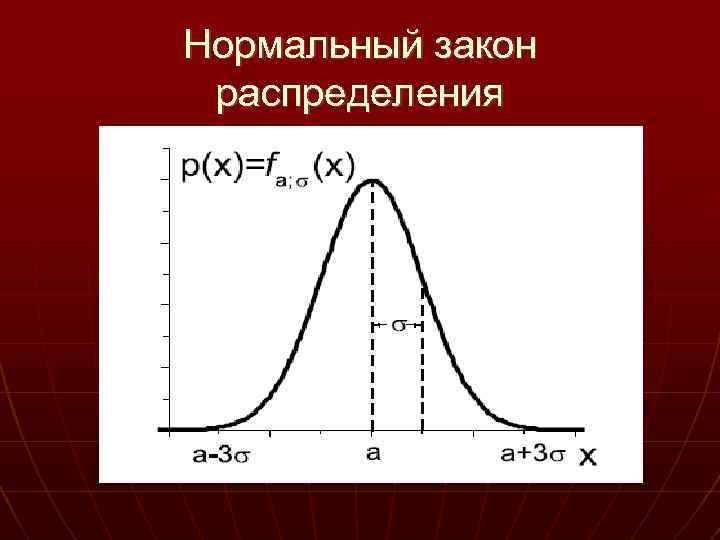
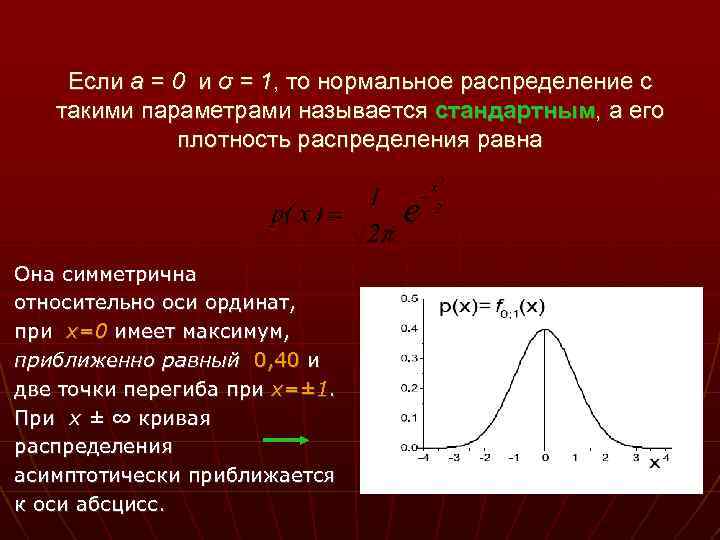Если a = 0 и σ = 1, то нормальное распределение с такими параметрами называется стандартным, а его плотность распределения равна Она симметрична относительно оси ординат, при x=0 имеет максимум, приближенно равный 0, 40 и две точки перегиба при x=± 1. При x ± ∞ кривая распределения асимптотически приближается к оси абсцисс.

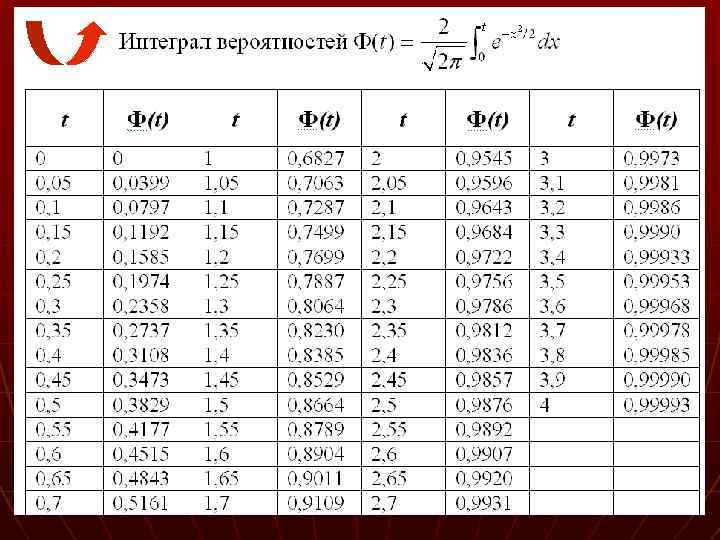
Интеграл нормального распределения не выражается через элементарные функции (попросту – не берется). Для расчета вероятностей случайных величин с нормальным законом распределения составлены таблицы специальной функции Таблица Интегралов вероятностей называемой интегралом вероятностей.

С помощью интеграла вероятностей можно вычислить вероятность попадания случайной величины со стандартным нормальным распределением в любой интервал

Расчет вероятностей в общем нормальном распределении производится с помощью интеграла вероятности Φ(t) следующим образом: где

Числовые характеристики распределения

Во многих вопросах практики нет необходимости характеризовать случайную величину полностью. Зачастую достаточно бывает указать только отдельные числовые параметры: какое-то среднее значение, около которого группируются возможные значения случайной величины; какое-либо число, характеризующее степень разбросанности этих значений относительно среднего и т. п. Среди большого количества таких числовых характеристик, применяемых в теории вероятности и математической статистике, мы рассмотрим две наиболее важные, а именно, математическое ожидание и дисперсию.

Математическое ожидание иногда называют просто средним значением случайной величины. Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности: - по своей сути аналог среднего арифметического для наблюдаемых в опытах значений случайной величины.

Математическим ожиданием (средним значением, центром распределения) непрерывной случайной величины называется интеграл от произведения ее значений на плотность распределения вероятностей:

Дисперсия, среднее квадратическое отклонение Дисперсией случайной величины X называют число D(X), равное математическому ожиданию (среднему) случайной величины (X-M(X))2, т. е. На практике часто используется следующая формула для вычисления дисперсии: Дисперсия случайной величины есть характеристика рассеивания, т. е. разбросанности значений случайной величины около ее математического ожидания.

Сама дисперсия имеет размерность квадрата случайной величины. Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина носит название среднее квадратическое отклонение:

Контрольные вопросы: Что называется перестановкой, размещением, сочетанием? Дайте определение случайного события. Какие события называются совместными, несовместными, противоположными, достоверными, невозможными? Что называется суммой, произведением случайных событий? Дайте различные определения вероятности. Какие свойства вероятностей Вы знаете? Сформулируйте формулу полной вероятности. Что такое «конкурирующая гипотеза» ? Что можно оценить, пользуясь формулой Байеса? Чем отличаются случайные величины дискретного и непрерывного типа? Как может быть задан закон распределения случайной величины? Опишите нормальный закон распределения. Что такое интеграл вероятностей? Какие Вы знаете численные характеристики распределения?