ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 9 класс Выполнила Ручкина Анна

ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 9 класс Выполнила: Ручкина Анна Ивановна, учитель математики МБОУ «СОШ № 22» АГО

Понятие вероятности В толковом словаре С. И. Ожегова и Н. Ю. Шведовой: «Вероятность – возможность исполнения, осуществимости чего-нибудь» . Основатель современной теории вероятностей А. Н. Колмогоров: «Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях» .

Вероятности случайных событий Под испытанием понимают некое действие, выполнение которого должно привести к одному из нескольких возможных результатов, или исходов, но при этом заранее неизвестно, к какому именно. Испытание состоит в бросании игрального кубика. Р МЕ Исходом является выпадение грани с определённым числом точек. И ПР Случайным событием при выполнении испытания называют наступление любого из исходов, отвечающих какому-либо заранее заданному требованию или условию. • При извлечении наугад одного шара из коробки с чёрными и белыми шарами извлечение какого-то конкретного шара — один из возможных исходов испытания, • а извлечение чёрного шара — случайное событие. Р МЕ И ПР

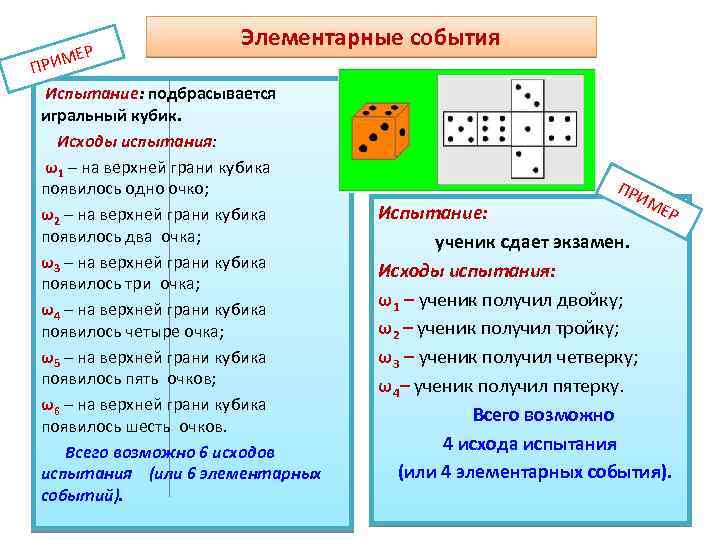Элементарные события ЕР РИМ П Испытание: подбрасывается игральный кубик. Исходы испытания: ω1 – на верхней грани кубика появилось одно очко; ω2 – на верхней грани кубика появилось два очка; ω3 – на верхней грани кубика появилось три очка; ω4 – на верхней грани кубика появилось четыре очка; ω5 – на верхней грани кубика появилось пять очков; ω6 – на верхней грани кубика появилось шесть очков. Всего возможно 6 исходов испытания (или 6 элементарных событий). ПР ИМ ЕР Испытание: ученик сдает экзамен. Исходы испытания: ω1 – ученик получил двойку; ω2 – ученик получил тройку; ω3 – ученик получил четверку; ω4– ученик получил пятерку. Всего возможно 4 исхода испытания (или 4 элементарных события).

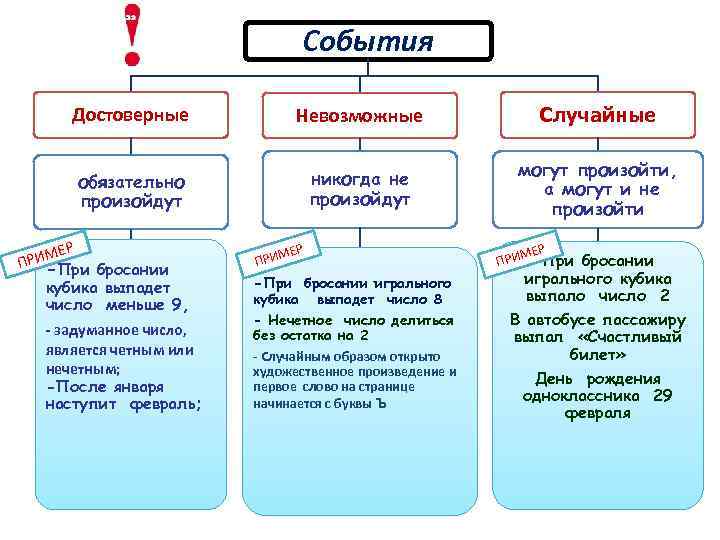События Достоверные Невозможные Случайные обязательно произойдут никогда не произойдут могут произойти, а могут и не произойти МЕР ПРИ-При бросании кубика выпадет число меньше 9, - задуманное число, является четным или нечетным; -После января наступит февраль; МЕР ПРИ -При бросании игрального кубика выпадет число 8 - Нечетное число делиться без остатка на 2 - Случайным образом открыто художественное произведение и первое слово на странице начинается с буквы Ъ МЕР ПРИ При бросании игрального кубика выпало число 2 В автобусе пассажиру выпал «Счастливый билет» День рождения одноклассника 29 февраля

запишите перечисленные ниже события, в соответствующий столбец таблицы: НЕВОЗМОЖНЫЕ Б, Д, ДОСТОВЕРНЫЕ Е, СЛУЧАЙНЫЕ А, В, Г, а) из 25 учащихся двое справляют день рождения 30 января; б) из 25 учащихся двое справляют день рождения 30 февраля; в) из списка 9 класса выбрали одного ученика и это – мальчик; г) из списка 9 класса выбрали одного ученика и это – девочка; д) из списка 9 класса выбрали одного ученика и ему – 14 месяцев; е) из списка 9 класса выбрали одного ученика и ему больше двух лет; ж) измерили стороны треугольника и сумма двух из них оказалась меньше длины третьей стороны.

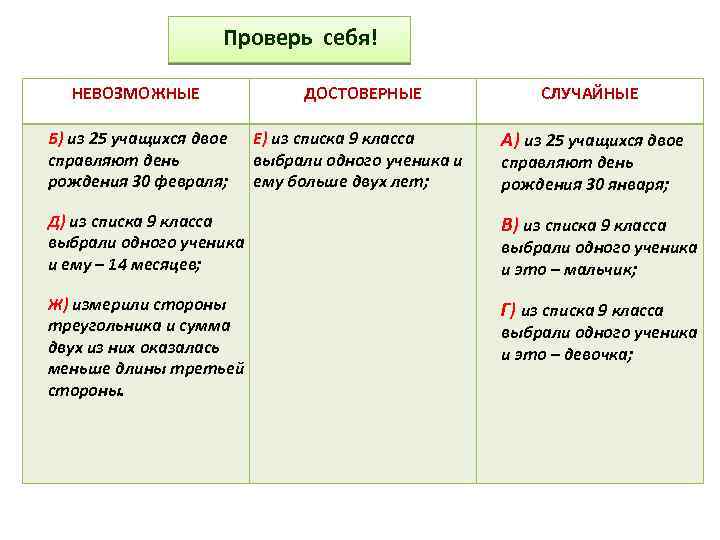Проверь себя! НЕВОЗМОЖНЫЕ ДОСТОВЕРНЫЕ СЛУЧАЙНЫЕ Б) из 25 учащихся двое справляют день рождения 30 февраля; Е) из списка 9 класса выбрали одного ученика и ему больше двух лет; А) из 25 учащихся двое справляют день рождения 30 января; Д) из списка 9 класса выбрали одного ученика и ему – 14 месяцев; В) из списка 9 класса Ж) измерили стороны треугольника и сумма двух из них оказалась меньше длины третьей стороны. Г) из списка 9 класса выбрали одного ученика и это – мальчик; выбрали одного ученика и это – девочка;

Если все исходы испытания равновозможны, то вероятностью Р(А) случайного события А называется отношение числа исходов, отвечающих условию события А, к общему числу исходов испытания. Р МЕ И ПР • При извлечении наугад шара из коробки с 7 чёрными и 3 белыми шарами вероятность извлечения чёрного шара:

Алгоритм вычисления вероятности случайного события А 1 2 3 • число N всех возможных исходов испытания; • число N(A) исходов, при которых наступает событие А; • отношение Вероятность любого события заключена в пределах от 0 до 1: 0< Р(А) <1. • При бросании игрального кубика возможны 6 различных исходов, Р • число исходов, при которых выпадает чётное число точек, равно МЕ И 3 (грани с 2, 4 и 6 точками), ПР • следовательно, вероятность выпадения грани с чётным числом точек равна

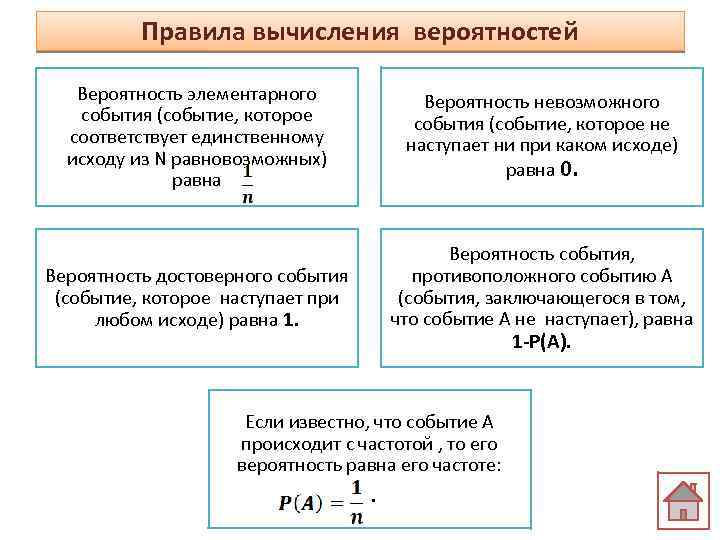Правила вычисления вероятностей Вероятность элементарного события (событие, которое соответствует единственному исходу из N равновозможных) равна Вероятность невозможного события (событие, которое не наступает ни при каком исходе) равна 0. Вероятность достоверного события (событие, которое наступает при любом исходе) равна 1. Вероятность события, противоположного событию А (события, заключающегося в том, что событие А не наступает), равна 1 -Р(А). Если известно, что событие А происходит с частотой , то его вероятность равна его частоте: .

Правило вычисления вероятности произведения событий. Произведением событий А и В называют событие А В, состоящее в наступлении обоих этих событий Если события А и В независимы (они происходят в разных испытаниях, и исход одного испытания не может влиять на исход другого), то вероятность того, что наступят оба этих события, равна Р(А)∙Р(В) Другими словами, вероятность произведения независимых событий равна произведению их вероятностей: • Р МЕ И ПР Событие А состоит в том, что при первом бросании игрального кубика выпало 6 очков, а событие В — в том, что при втором бросании игрального кубика выпало 6 очков. Тогда произведение этих событий — это выпадение двух шестёрок при двукратном бросании кубика. Поскольку результат одного бросания не зависит от результата другого бросания, события А и В независимы. Следовательно, вероятность выпадения двух шестёрок подряд равна

Правило вычисления вероятности суммы событий Суммой событий А и В называют событие А + В, состоящее в наступлении хотя бы одного из этих событий. Если события А и В несовместны (они не могут происходить одновременно), то вероятность того, что наступит хотя бы одно из этих событий, равна Р(А) + Р(В). Другими словами, вероятность суммы несовместных событий равна сумме их вероятностей: • При стрельбе по мишени спортсмен с вероятностью 0, 2 Р МЕ И попадает в десятку, а с вероятностью 0, 4 — в девятку. Для ПР одного выстрела попадание в десятку (событие А) и попадание в девятку (событие Б) несовместны, поскольку не могут произойти одновременно. Следовательно, вероятность набрать не менее 9 очков при одном выстреле (вероятность суммы событий А и В) равна • Р(А + В) = Р(А) + Р(В) = 0, 2+0, 4 = 0, 6.

Понятие геометрической вероятности А A 1 /////// B 1 В х Вероятность того, что точка, случайным образом выбранная на отрезке АВ, окажется принадлежащей отрезку A 1 B 1 целиком содержащемуся в отрезке АВ, равна отношению длин этих отрезков: Р МЕ И ПР На отрезке [0; 5] выбрано произвольное число. Вероятность того, что оно удовлетворяет неравенству 2 ≤x ≤ 4, равна отношению длины отрезка [2; 4] к длине отрезка [0; 5]:

F′ F Вероятность того, что точка, случайным образом выбранная из фигуры F, окажется принадлежащей фигуре F ′ целиком содержащейся в фигуре F, равна отношению площадей этих фигур: 2 Р МЕ Площадь поверхности Земли — 510 млн км , суша занимает И ПР площадь 150 млн км 2. Вероятность того, что метеорит, случайным образом падающий на Землю, упадёт на сушу, равна