Элементы теории поля Автор И В Дайняк к

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Лекция 5 ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Скалярное поле Пример: Найти поверхности уровня скалярного поля Поверхностями уровня являются эллиптические параболоиды

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Скалярное поле Градиент скалярного поля: Скорость изменения скалярного поля в направлении вектора:

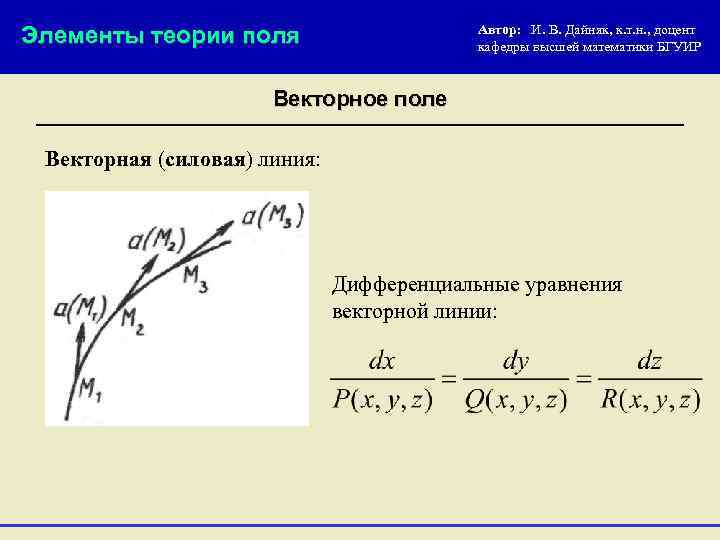Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Векторное поле Векторная (силовая) линия: Дифференциальные уравнения векторной линии:

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Поток векторного поля Общий случай: Поток через замкнутую поверхность:

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Дивергенция векторного поля Рассмотрим отношение Дивергенция:

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Дивергенция векторного поля В прямоугольной декартовой системе координат: Дивергенция: Теорема Остроградского:

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Циркуляция векторного поля

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Ротор векторного поля Преобразуем циркуляцию по формуле Стокса: Ротор векторного поля:

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Ротор векторного поля Ротор можно формально получить из определителя: Формула Стокса:

Элементы теории поля Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР Соленоидальное и потенциальное векторное поле Векторное поле является соленоидальным, или трубчатым, если Векторное поле является потенциальным, или безвихревым, если что равносильно выполнению следующих условий:

Высшая математика Автор: И. В. Дайняк, к. т. н. , доцент кафедры высшей математики БГУИР math. mmts-it. org