Элементы теории графов 2 Лекция № 10









10. Элементы теории графов 2.ppt
- Количество слайдов: 16
 Элементы теории графов 2 Лекция № 10
Элементы теории графов 2 Лекция № 10
 Вопросы • Задача о максимальном потоке • Сетевая модель
Вопросы • Задача о максимальном потоке • Сетевая модель
 Задача о максимальном потоке • Рассматривается сеть трубопроводов для транспортировки сырой нефти от буровых скважин до нефтеперегонных заводов. Для перекачки нефти предусмотрены магистральные насосные станции. • Каждый сегмент сети имеет свою пропускную способность. Сегменты трубопровода могут быть одно и двунаправленными. • Определить максимальную пропускную способность сети трубопроводов.
Задача о максимальном потоке • Рассматривается сеть трубопроводов для транспортировки сырой нефти от буровых скважин до нефтеперегонных заводов. Для перекачки нефти предусмотрены магистральные насосные станции. • Каждый сегмент сети имеет свою пропускную способность. Сегменты трубопровода могут быть одно и двунаправленными. • Определить максимальную пропускную способность сети трубопроводов.
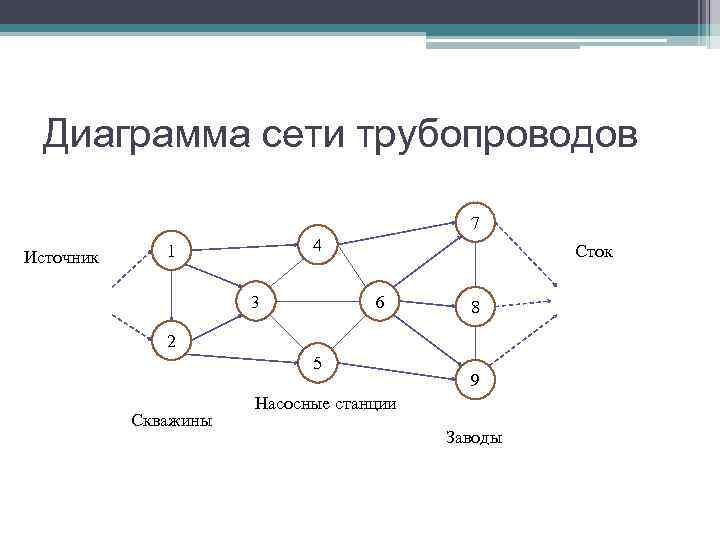
 Диаграмма сети трубопроводов 7 1 4 Сток Источник 3 6 8 2 5 9 Насосные станции Скважины Заводы
Диаграмма сети трубопроводов 7 1 4 Сток Источник 3 6 8 2 5 9 Насосные станции Скважины Заводы
 Перебор разрезов • Разрез – это множество ребер, при удалении которых из сети полностью прекращается поток от источника к стоку. • Пропускная способность разреза равна сумме пропускных способностей «разрезанных ребер» . • Среди всех разрезов сети разрез с минимальной пропускной способностью определяет максимальный поток в сети.
Перебор разрезов • Разрез – это множество ребер, при удалении которых из сети полностью прекращается поток от источника к стоку. • Пропускная способность разреза равна сумме пропускных способностей «разрезанных ребер» . • Среди всех разрезов сети разрез с минимальной пропускной способностью определяет максимальный поток в сети.
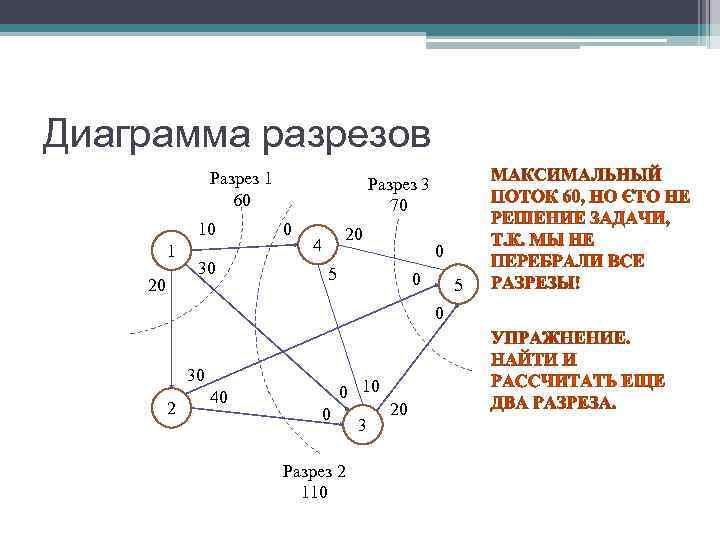
 Диаграмма разрезов Разрез 1 Разрез 3 60 70 10 0 20 1 4 0 30 5 20 0 5 0 30 40 0 10 2 0 20 3 Разрез 2 110
Диаграмма разрезов Разрез 1 Разрез 3 60 70 10 0 20 1 4 0 30 5 20 0 5 0 30 40 0 10 2 0 20 3 Разрез 2 110
 Алгоритм нахождения максимального потока. 1. Для всех ребер (i, j) положим остаточную пропускную способность равной первоначальной, т. е. . Назначим и пометим узел 1 меткой [ , -]. Полагаем i = 1 и переходим к шагу 2. 2. Определяем множество Si узлов, в которые можно пройти по ребру с положительной остаточной пропускной способностью. Если Si переходим шагу 3, иначе к шагу 4.
Алгоритм нахождения максимального потока. 1. Для всех ребер (i, j) положим остаточную пропускную способность равной первоначальной, т. е. . Назначим и пометим узел 1 меткой [ , -]. Полагаем i = 1 и переходим к шагу 2. 2. Определяем множество Si узлов, в которые можно пройти по ребру с положительной остаточной пропускной способностью. Если Si переходим шагу 3, иначе к шагу 4.
 Алгоритм нахождения максимального потока. 3. Во множестве Si находим такой узел k, что . Положим и пометим узел k меткой [ak, i]. Если последней меткой помечен узел стока, переходим к шагу 5, иначе полагаем i = k и переходим ко второму шагу. 4. (откат) Если i = 1, переходим к шагу 6, иначе находим помеченный узел r, непосредственно предшествующий узлу i и удаляем узел i из множества узлов смежных с узлом r. Полагаем i = r и переходим к второму шагу.
Алгоритм нахождения максимального потока. 3. Во множестве Si находим такой узел k, что . Положим и пометим узел k меткой [ak, i]. Если последней меткой помечен узел стока, переходим к шагу 5, иначе полагаем i = k и переходим ко второму шагу. 4. (откат) Если i = 1, переходим к шагу 6, иначе находим помеченный узел r, непосредственно предшествующий узлу i и удаляем узел i из множества узлов смежных с узлом r. Полагаем i = r и переходим к второму шагу.
 Алгоритм нахождения максимального потока. 5. Определение остаточной сети. Обозначим за множество узлов, через которые проходит p-ый найденный сквозной путь от узла 1 до узла n. Тогда максимальный поток, проходящий по нему, вычисляется как . Остаточные пропускные способности ребер этого пути уменьшаются на величину fp в направлении потока и увеличиваются на эту же величину в противоположном направлении.
Алгоритм нахождения максимального потока. 5. Определение остаточной сети. Обозначим за множество узлов, через которые проходит p-ый найденный сквозной путь от узла 1 до узла n. Тогда максимальный поток, проходящий по нему, вычисляется как . Остаточные пропускные способности ребер этого пути уменьшаются на величину fp в направлении потока и увеличиваются на эту же величину в противоположном направлении.
 Завершение алгоритма • Далее восстанавливаем все узлы удаленные на шаге 4. Полагаем i = 1 и возвращаемся ко второму шагу. 6. Решение. При m найденных сквозных путях максимальный поток вычисляется по формуле
Завершение алгоритма • Далее восстанавливаем все узлы удаленные на шаге 4. Полагаем i = 1 и возвращаемся ко второму шагу. 6. Решение. При m найденных сквозных путях максимальный поток вычисляется по формуле
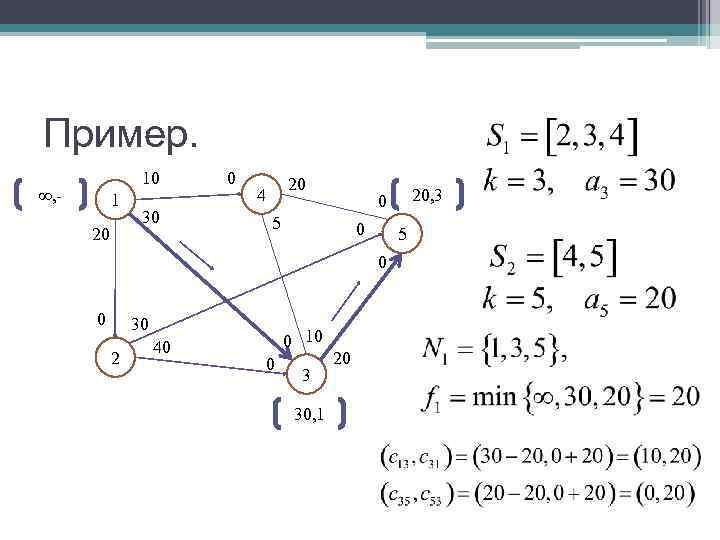
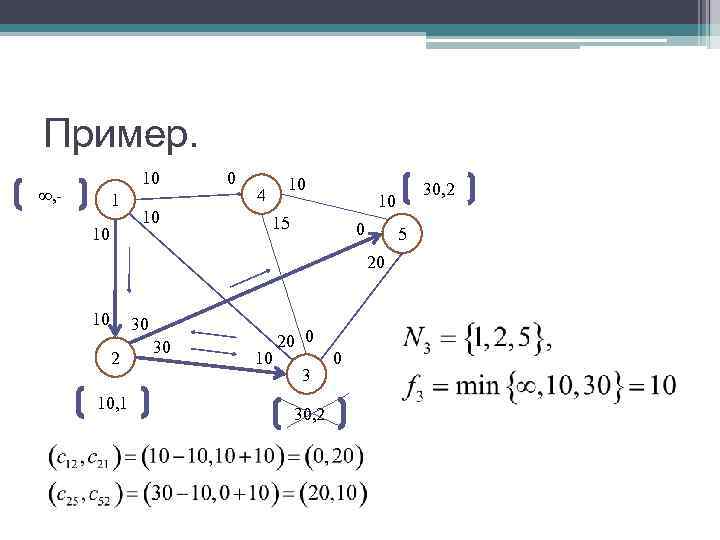
 Пример. 10 0 20 , - 1 4 0 20, 3 30 5 20 0 5 0 0 30 40 0 10 2 0 20 30, 1
Пример. 10 0 20 , - 1 4 0 20, 3 30 5 20 0 5 0 0 30 40 0 10 2 0 20 30, 1
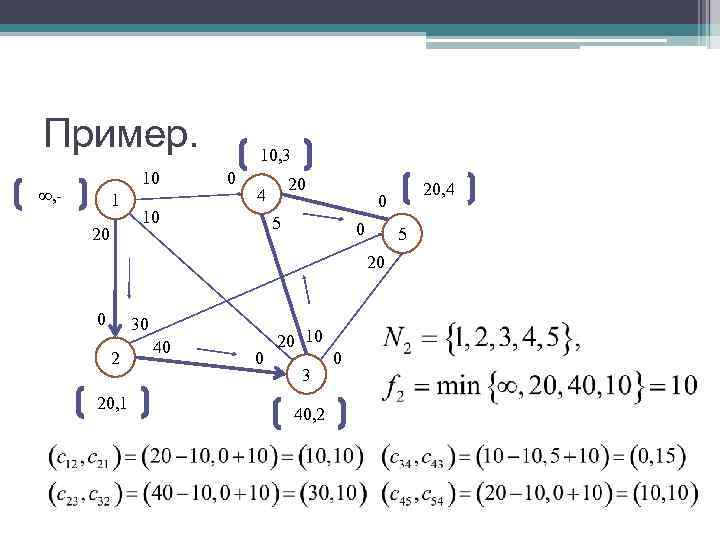
 Пример. 10, 3 10 0 20 , - 4 20, 4 1 0 10 5 20 0 5 20 0 30 40 20 10 2 0 3 20, 1 40, 2
Пример. 10, 3 10 0 20 , - 4 20, 4 1 0 10 5 20 0 5 20 0 30 40 20 10 2 0 3 20, 1 40, 2
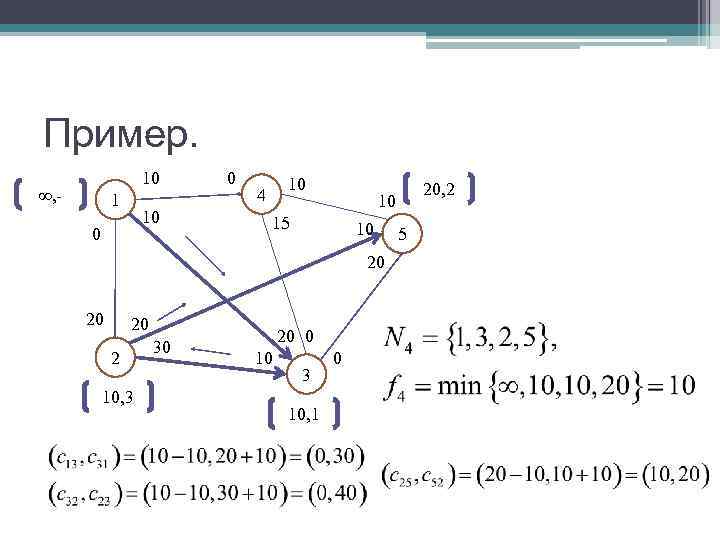
 Пример. 10 0 10 , - 4 30, 2 1 10 15 10 0 5 20 10 30 20 0 2 10 3 10, 1 30, 2
Пример. 10 0 10 , - 4 30, 2 1 10 15 10 0 5 20 10 30 20 0 2 10 3 10, 1 30, 2
 Пример. 10 0 10 , - 4 20, 2 1 10 15 0 10 5 20 20 0 30 2 10 0 3 10, 3 10, 1
Пример. 10 0 10 , - 4 20, 2 1 10 15 0 10 5 20 20 0 30 2 10 0 3 10, 3 10, 1
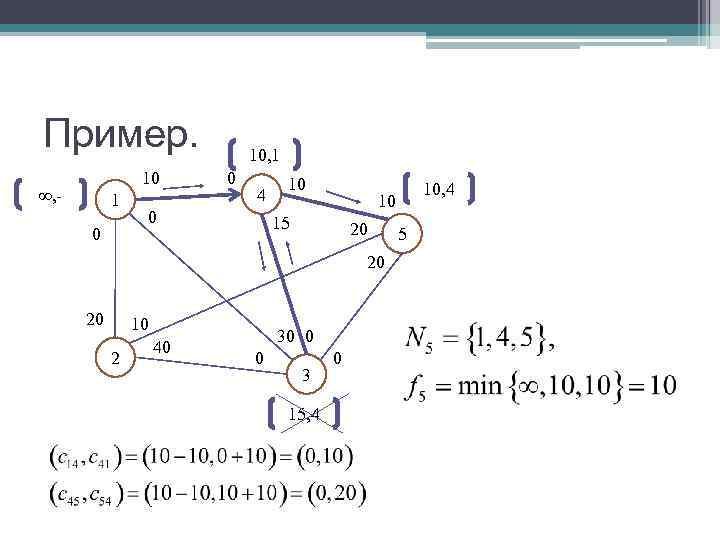
 Пример. 10, 1 10 0 10 , - 4 10, 4 1 10 15 0 20 5 20 10 30 0 40 2 0 3 15, 4
Пример. 10, 1 10 0 10 , - 4 10, 4 1 10 15 0 20 5 20 10 30 0 40 2 0 3 15, 4
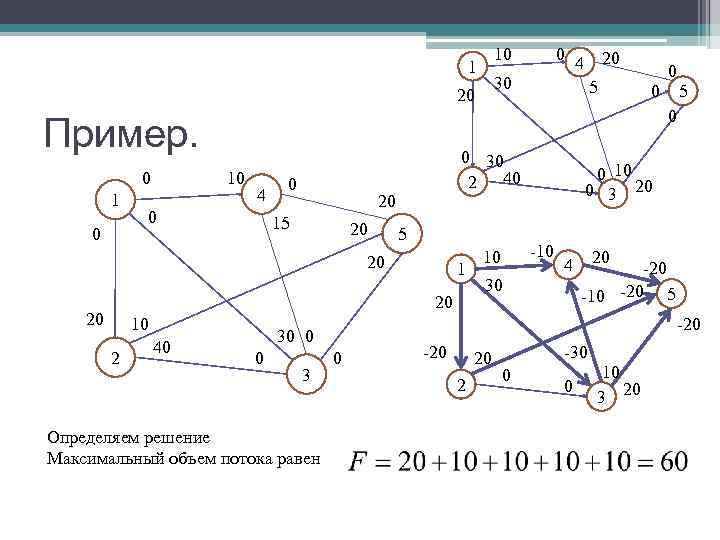
 10 0 4 20 1 0 30 5 0 5 20 0 Пример. 0 30 0 10 2 40 0 10 0 3 20 1 4 20 15 0 20 5 10 -10 20 1 4 -20 30 20 -10 -20 5 20 10 -20 30 0 40 -20 -30 2 0 0 20 3 0 10 2 0 3 20 Определяем решение Максимальный объем потока равен
10 0 4 20 1 0 30 5 0 5 20 0 Пример. 0 30 0 10 2 40 0 10 0 3 20 1 4 20 15 0 20 5 10 -10 20 1 4 -20 30 20 -10 -20 5 20 10 -20 30 0 40 -20 -30 2 0 0 20 3 0 10 2 0 3 20 Определяем решение Максимальный объем потока равен

