Элементы статистической обработки данных.ppt
- Количество слайдов: 27

Элементы статистической обработки данных Выборочный метод Вариационные ряды Выборочная функция распределения

Математическая статистика возникла и создавалась параллельно с теорией вероятностей в XVII веке. Дальнейшее развитие математической статистики (вторая половина XIX и начало XX веков) обязано, в первую очередь, П. Л. Чебышеву, А. А. Маркову, А. М. Ляпунову и др.

Математическая статистика n Описательная статистика охватывает методы описания статистических данных, представления их в виде таблиц, распределений и т. п. n Аналитическая статистика (теория статистических выводов) ориентирована на обработку данных, полученных в ходе эксперимента, с целью формулировки выводов, имеющих прикладное значение

Величины n Случайной называется величина, принимающая в опыте (или при наблюдении) определенное, но наперед неизвестное значение, зависящее от случайных причин, которые заранее не могут быть учтены. n Случайные величины могут быть дискретными (прерывными) и непрерывными. n Дискретной (прерывной) называется случайная величина, которая может принимать только конечное или счетное число значений. n Непрерывной называется случайная величина, которая может принимать любое значение из некоторого замкнутого или открытого интервала, в т. ч. и бесконечного.

Выборочный метод Каждый объект статистического наблюдения состоит из отдельных элементов – единиц наблюдения. Результаты статистических наблюдений представляют собой числовую информацию – данные. n Статистические данные – это сведения о том, какие значения принял интересующий исследователя признак в статистической совокупности. n Статистическая совокупность называется генеральной совокупностью, если исследованию подлежат все элементы совокупности.

Выборочный метод n Выборочной совокупностью, или просто выборкой, называют часть элементов генеральной совокупности подлежащих исследованию. (Если некоторая совокупность слишком многочисленна, либо элементы малодоступны и т. п. , прибегают к изучению части совокупности. ) n Ряд значений признака, расположенный в порядке возрастания или убывания, называется вариационным рядом. n Частота (mi) показывает, сколько раз встречается тот или иной вариант в статистической совокупности.
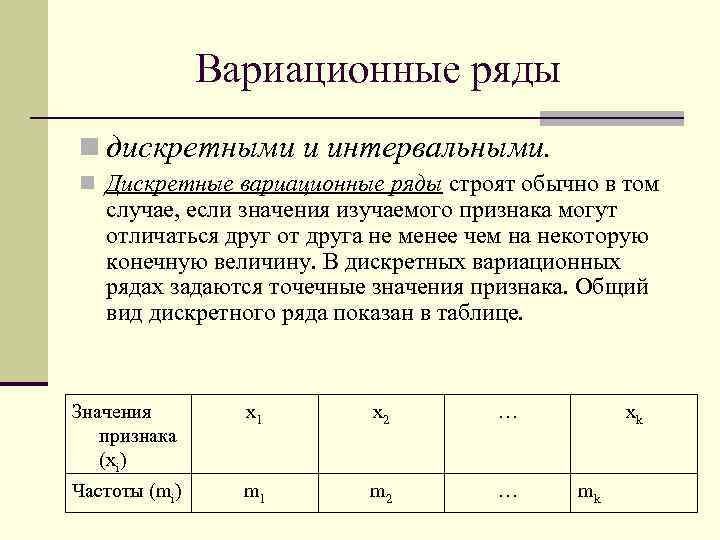
Вариационные ряды n дискретными и интервальными. n Дискретные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга не менее чем на некоторую конечную величину. В дискретных вариационных рядах задаются точечные значения признака. Общий вид дискретного ряда показан в таблице. Значения признака (хi) х1 х2 … Частоты (mi) m 1 m 2 … хk mk
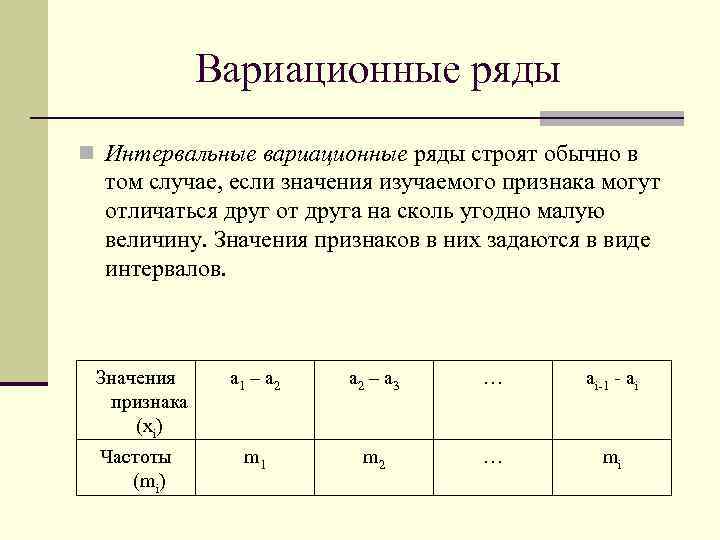
Вариационные ряды n Интервальные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга на сколь угодно малую величину. Значения признаков в них задаются в виде интервалов. Значения признака (хi) Частоты (mi) a 1 – a 2 – a 3 … ai-1 - ai m 1 m 2 … mi

Вариационные ряды n В интервальных вариационных рядах в каждом интервале выделяют верхнюю и нижнюю границы. n Разность между верхней и нижней границами интервала называется интервальной разностью или длиной интервала. В общем виде интервальную разность ki представим как n ki = xi (max) - xi (min) Первый и последний интервалы могут быть открытыми, т. е. иметь только одну границу.
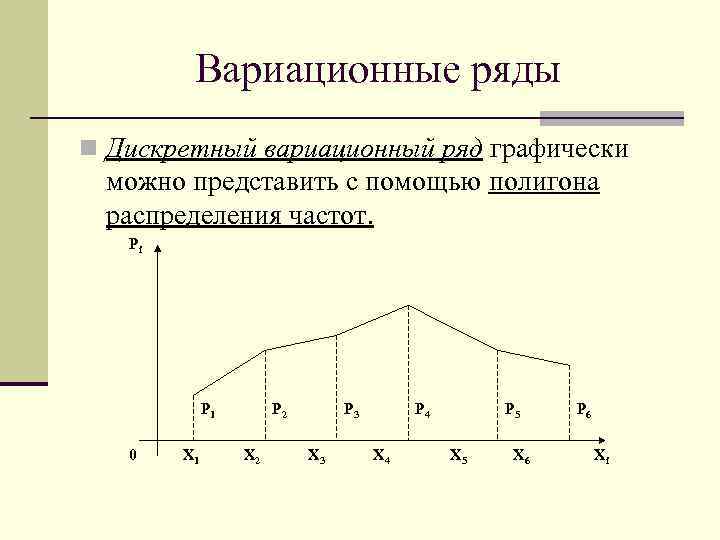
Вариационные ряды n Дискретный вариационный ряд графически можно представить с помощью полигона распределения частот. Pi P 1 0 X 1 P 2 X 2 P 3 X 3 P 4 X 4 P 5 X 6 P 6 Xi
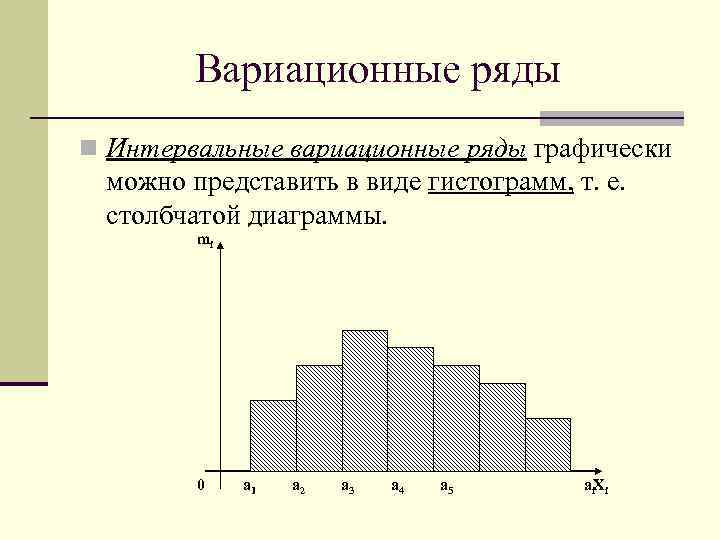
Вариационные ряды n Интервальные вариационные ряды графически можно представить в виде гистограмм, т. е. столбчатой диаграммы. mi 0 a 1 a 2 a 3 a 4 a 5 ai. Xi

Числовые характеристики вариационного ряда Одной из основных характеристик ряда распределения является средняя арифметическая. где хi – i-е значение признака; n – объём ряда (число наблюдений).

Показатели вариации Математическое ожидание – это числовая характеристика случайной величины, со средним арифметическим её наблюдаемых значений, которое является статистической характеристикой вариационного ряда и рассчитывается по формуле: где рi – вероятность i-го значения признака.

Показатели вариации Дисперсия Среднее квадратичное отклонение Коэффициент вариации

Выборочная функция распределения n Числовые характеристики распределения вероятностей случайной величины опираются на знание закона ее распределения F(x). n Для выборки x 1, x 2, …xn выборочная (эмпирическая) функция распределения равна доле таких значений xi, что

Выборочная функция распределения n мода – элемент выборки, который встречается наиболее часто. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9) n Среднее значение выборки (аналог мат. ожидания) n Медиана – число, которое является серединой выборки n Интервал (амплитуда, вариационный размах) – разница между максимальным и минимальным значениями выборки

Выборочная функция распределения n Дисперсия выборки – параметр, характеризующий степень разброса элементов выборки относительно среднего значения. n Выборочное стандартное отклонение n Стандартная ошибка (ошибка среднего)

Статистические таблицы Перед анализом и интерпретацией данных их обобщают. Ранжирование – упорядочение значений от максимального до минимального или наоборот. Такое упорядочивание называется несгруппированным рангом. Распределение частот. Проранжированный список сворачивают, указывая все полученные измерения подряд, однократно, а в соседней графе указывают частоту, с которой встречается данная оценка

Статистические таблицы Распределение сгруппированных частот применяется при большом количестве оценок (100 и более). Оценки группируются по признакам и каждая такая группа называется разрядом оценок. В случае полного поглощения этими группами всех данных, мы говорим о распределении сгруппированных частот.

Статистические таблицы n Для построения выборочной функции распределения весь диапазон разбивают на ряд интервалов одинаковой ширины. (число интервалов не менее 5 и не более 15) n Затем определяют число значений случайной величины, попавших в каждый интервал. По найденным относительным частотам строят гистограмму выборочной функции распределения.

значения Интервал Подсчет Частота 90 95 51 112 110 -114 1 1 66 78 109 62 105 -109 111 3 106 70 89 91 100 -104 11 2 84 47 58 93 95 -99 1111 4 105 95 59 84 90 -94 111 3 83 100 72 85 -89 1 1 104 69 74 80 -89 111111 6 82 44 75 75 -79 1111 4 97 80 81 70 -74 1111 4 97 75 71 65 -69 111 3 59 75 68 60 -64 1 1 55 -59 111 3 50 -54 1 1 45 -49 1 1 44 -45 1 1

Наглядное представление данных В табличных процессорах представляется возможность оформить численные данные в виде графика или диаграммы различного вида. Примеры диаграмм и графиков: линейная, столбиковая, полосчатая, кумулятивная кривая, пиктограмма – данные представляются в виде стилизованных изображений (улов рыбы в виде рыбы), логарифмическая диаграмма, круговая диаграмма.

Наглядное представление данных Гистограмма - это последовательность столбцов, каждый из которых опирается на один раздельный интервал, а высота столбца – это частота или количество случаев. Принято распределять горизонтальную шкалу на один раздельный интервал вправо и влево от полученного диапазона. Середина столбца совмещается с срединой интервала, на практике ее изображают в форме контура, опуская вертикальные линии.

Наглядное представление данных Полигон распределения – это та же гистограмма, но линии соединяют середины столбцов каждого разрядного интервала. Гистограмма наиболее легка для восприятия и используется в тех случаях когда всего одно распределение. Если надо сравнить два и более распределений, используют полигон, чтобы избежать запутанной картины.

Процедура Гистограмма в Ms Excel n Используется для получения выборочных и интегральных частот попадания данных в указанные интервалы значений

Процедура Гистограмма в Ms Excel n Медиана случайной величины – такое ее значение, которое делит площадь гистограммы пополам. n Мода распределения случайной величины – такое ее значение (такой интервал), при котором гистограмма достигает максимума. n Стандартное отклонение – среднеквадратичное отклонение от среднего арифметического. n Дисперсия выборки – математическое ожидание квадрата отклонения случайной величины от своего математического ожидания (квадрат стандартного отклонения).

Процедура Гистограмма в Ms Excel n Эксцесс характеризует островершинность кривой. У n n нормального распределения он равен 0 и может быть использован для выяснения отклонения распределения от нормального. Асимметричность характеризует симметрию распределения. У нормального распределения она равна 0 и может быть использована для выяснения отклонения распределения от нормального. Интервал – это размах, т. е. разность между указываемыми ниже максимумом и минимумом. Сумма – сумма значений. Счет – количество.
Элементы статистической обработки данных.ppt