элементы статики.pptx
- Количество слайдов: 27
 элементы статики
элементы статики
 Статика – раздел механики, в котором изучают условия равновесия твердых, жидких и газообразных тел под действием сил. Равновесие тела – это сохранение состояния его движения с течением времени. Положением равновесия материальной точки относительно данного тела называется такое ее движение, при котором взаимное расположение материальной точки и этого тела остается неизменным.
Статика – раздел механики, в котором изучают условия равновесия твердых, жидких и газообразных тел под действием сил. Равновесие тела – это сохранение состояния его движения с течением времени. Положением равновесия материальной точки относительно данного тела называется такое ее движение, при котором взаимное расположение материальной точки и этого тела остается неизменным.
 Условие равновесия материальной точки – это равенство нулю суммы всех сил, действующих на него. Равновесие абсолютно твердого тела, при условии, что кинематические связи допускают только его поступательное движение, совпадает с условием равновесия материальной точки, то есть – это равенство нулю суммы всех сил, действующих на него. Механические связи – это ограничения, наложенные на положение или движение рассматриваемой системы в пространстве. Механические связи осуществляются посредством каких-либо тел – стержней, нитей, шарниров, подшипников и др.
Условие равновесия материальной точки – это равенство нулю суммы всех сил, действующих на него. Равновесие абсолютно твердого тела, при условии, что кинематические связи допускают только его поступательное движение, совпадает с условием равновесия материальной точки, то есть – это равенство нулю суммы всех сил, действующих на него. Механические связи – это ограничения, наложенные на положение или движение рассматриваемой системы в пространстве. Механические связи осуществляются посредством каких-либо тел – стержней, нитей, шарниров, подшипников и др.
 Абсолютно твердое тело с закрепленной (неподвижной) осью вращения находится в равновесии если сумма моментов всех внешних сил относительно этой оси равна нулю. Если абсолютно твердое тело может перемещаться поступательно, а также совершать вращательное движение вокруг некоторой оси, то равновесие тела достигается при одновременном соблюдении двух условий:
Абсолютно твердое тело с закрепленной (неподвижной) осью вращения находится в равновесии если сумма моментов всех внешних сил относительно этой оси равна нулю. Если абсолютно твердое тело может перемещаться поступательно, а также совершать вращательное движение вокруг некоторой оси, то равновесие тела достигается при одновременном соблюдении двух условий:
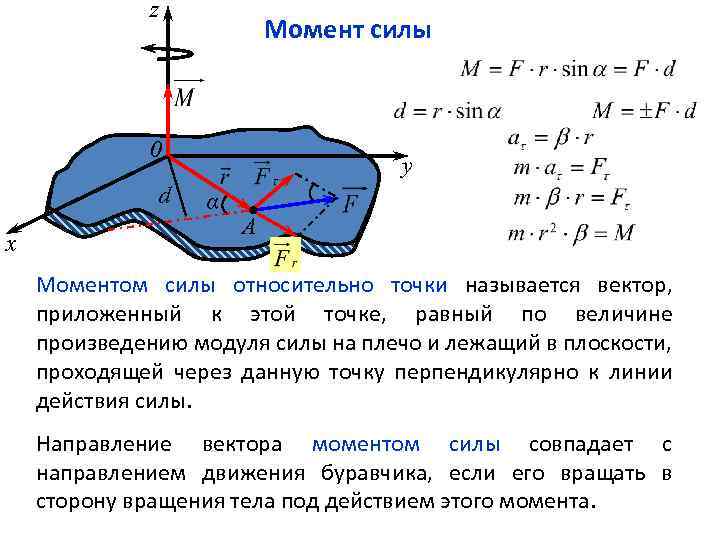 z Момент силы 0 d x y α A Моментом силы относительно точки называется вектор, приложенный к этой точке, равный по величине произведению модуля силы на плечо и лежащий в плоскости, проходящей через данную точку перпендикулярно к линии действия силы. Направление вектора моментом силы совпадает с направлением движения буравчика, если его вращать в сторону вращения тела под действием этого момента.
z Момент силы 0 d x y α A Моментом силы относительно точки называется вектор, приложенный к этой точке, равный по величине произведению модуля силы на плечо и лежащий в плоскости, проходящей через данную точку перпендикулярно к линии действия силы. Направление вектора моментом силы совпадает с направлением движения буравчика, если его вращать в сторону вращения тела под действием этого момента.
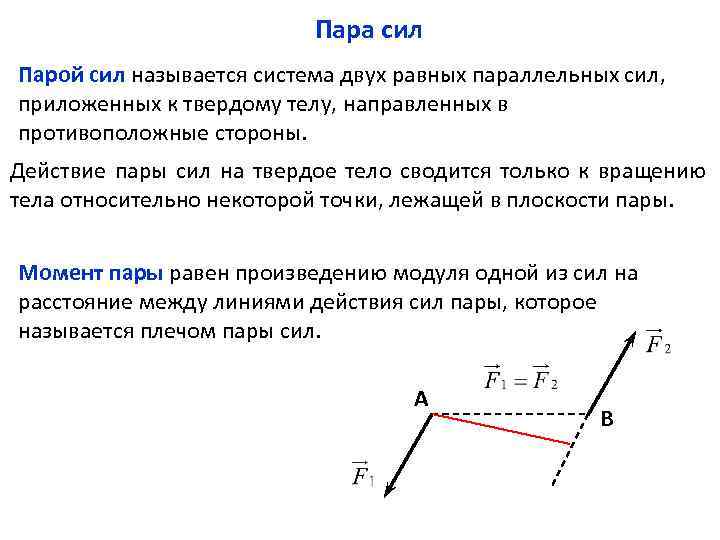 Пара сил Парой сил называется система двух равных параллельных сил, приложенных к твердому телу, направленных в противоположные стороны. Действие пары сил на твердое тело сводится только к вращению тела относительно некоторой точки, лежащей в плоскости пары. Момент пары равен произведению модуля одной из сил на расстояние между линиями действия сил пары, которое называется плечом пары сил. А В
Пара сил Парой сил называется система двух равных параллельных сил, приложенных к твердому телу, направленных в противоположные стороны. Действие пары сил на твердое тело сводится только к вращению тела относительно некоторой точки, лежащей в плоскости пары. Момент пары равен произведению модуля одной из сил на расстояние между линиями действия сил пары, которое называется плечом пары сил. А В
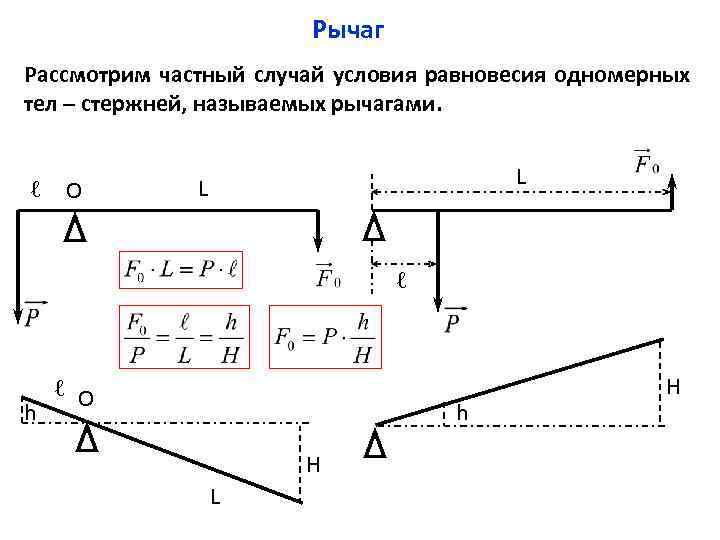 Рычаг Рассмотрим частный случай условия равновесия одномерных тел – стержней, называемых рычагами. ℓ О L L ℓ h ℓ О h H L H
Рычаг Рассмотрим частный случай условия равновесия одномерных тел – стержней, называемых рычагами. ℓ О L L ℓ h ℓ О h H L H
 Виды равновесия Различают три вида равновесия тела: 1. Устойчивое равновесие, если тело, выведенное из положения равновесия в соседнее ближайшее положение и затем предоставленное самому себе, вернется в это положение. 2. Неустойчивое равновесие, если тело, выведенное из положения равновесия в соседнее ближайшее положение и затем предоставленное самому себе, будет еще больше отклоняться от этого положения. 3. Безразличное равновесие, если тело, выведенное из положения равновесия в соседнее ближайшее положение и затем предоставленное самому себе, остается в новом своем положении.
Виды равновесия Различают три вида равновесия тела: 1. Устойчивое равновесие, если тело, выведенное из положения равновесия в соседнее ближайшее положение и затем предоставленное самому себе, вернется в это положение. 2. Неустойчивое равновесие, если тело, выведенное из положения равновесия в соседнее ближайшее положение и затем предоставленное самому себе, будет еще больше отклоняться от этого положения. 3. Безразличное равновесие, если тело, выведенное из положения равновесия в соседнее ближайшее положение и затем предоставленное самому себе, остается в новом своем положении.
 Центр масс Определение центра масс: Точка тела, в которой сосредоточена вся его масса, и движущаяся так, как если бы на нее действовали только внешние силы, называется центром масс тела. Формула для расчета координат центра масс: Импульс твердого тела: Импульс твердого тела равен импульсу материальной точки, масса которой равна массе тела, а скорость равна скорости центра масс.
Центр масс Определение центра масс: Точка тела, в которой сосредоточена вся его масса, и движущаяся так, как если бы на нее действовали только внешние силы, называется центром масс тела. Формула для расчета координат центра масс: Импульс твердого тела: Импульс твердого тела равен импульсу материальной точки, масса которой равна массе тела, а скорость равна скорости центра масс.
 Теорема о движении центра масс: Центр масс твердого тела движется так же, как двигалась бы материальная точка, масса которой равна массе тела, под действием внешних сил, приложенных к этому телу Следствие теоремы о движении центра масс: Если сумма внешних сил, действующих на тело равна нулю, то его центр масс покоится или движется прямолинейно и равномерно.
Теорема о движении центра масс: Центр масс твердого тела движется так же, как двигалась бы материальная точка, масса которой равна массе тела, под действием внешних сил, приложенных к этому телу Следствие теоремы о движении центра масс: Если сумма внешних сил, действующих на тело равна нулю, то его центр масс покоится или движется прямолинейно и равномерно.
 Примеры решения задач ц x Тонкий однородный стержень длиной ℓ и массой m привели в движение по гладкой горизонтальной поверхности так, что он движется поступательно и одновременно вращается с угловой скоростью ω. Найдите натяжение стержня на расстоянии x от его центра. Перейдем в ИСО, связанную с центром стержня и рассмотрим движение куска стержня, заключенного между рассматриваемой точкой и его концом. Масса рассматриваемого куска Центр масс рассматриваемо куска движется по окружности радиусом
Примеры решения задач ц x Тонкий однородный стержень длиной ℓ и массой m привели в движение по гладкой горизонтальной поверхности так, что он движется поступательно и одновременно вращается с угловой скоростью ω. Найдите натяжение стержня на расстоянии x от его центра. Перейдем в ИСО, связанную с центром стержня и рассмотрим движение куска стержня, заключенного между рассматриваемой точкой и его концом. Масса рассматриваемого куска Центр масс рассматриваемо куска движется по окружности радиусом
 ЗАДАЧИ
ЗАДАЧИ
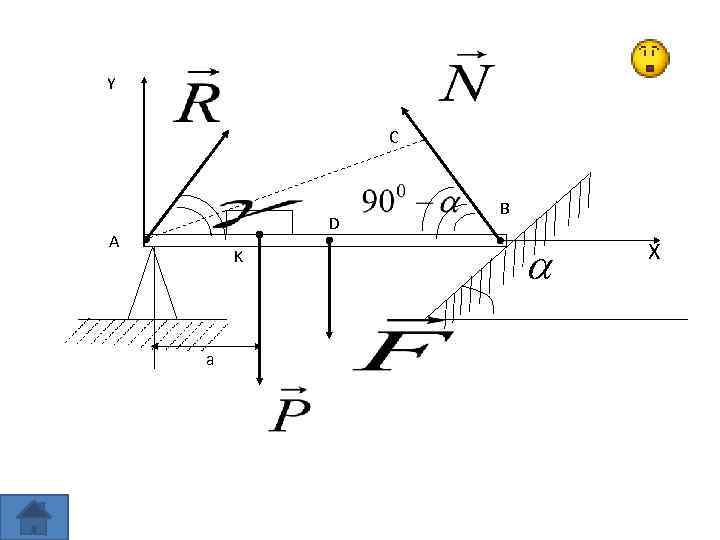
 Задача № 3 Однородная балка, длиной 2 l и массой m, расположенная горизонтально, одним концом шарнирно закреплена в точке А. Другой конец балки опирается в точке В на гладкую плоскость, наклонённую под углом α. На балке на расстоянии а от шарнира А расположен груз массой m¹. Найдите силы реакции шарнира и плоскости. Трение в шарнире отсутствует.
Задача № 3 Однородная балка, длиной 2 l и массой m, расположенная горизонтально, одним концом шарнирно закреплена в точке А. Другой конец балки опирается в точке В на гладкую плоскость, наклонённую под углом α. На балке на расстоянии а от шарнира А расположен груз массой m¹. Найдите силы реакции шарнира и плоскости. Трение в шарнире отсутствует.
 Y C D A K a B a Х
Y C D A K a B a Х
 Решение Т. к. балка в равновесии, то сумма моментов сил относительно шарнира равна нулю: Найдём плечи сил:
Решение Т. к. балка в равновесии, то сумма моментов сил относительно шарнира равна нулю: Найдём плечи сил:
 Для нахождения силы реакции шарнира воспользуемся первым условием равновесия:
Для нахождения силы реакции шарнира воспользуемся первым условием равновесия:
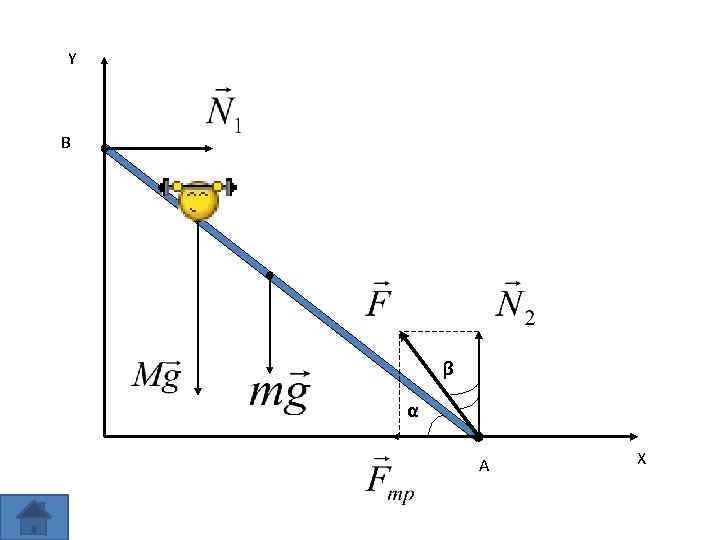
 Задача № 4 Лестница длиной l = 3 м стоит, упираясь верхним закруглённым концом в гладкую стену, а нижним в пол. Угол наклона лестницы к горизонту α = 60°, её масса m=15 кг. На лестнице на расстоянии а=1 м от её верхнего конца стоит человек массой М = 60 кг. С какой силой давит пол на нижний конец лестницы и как направлена эта сила?
Задача № 4 Лестница длиной l = 3 м стоит, упираясь верхним закруглённым концом в гладкую стену, а нижним в пол. Угол наклона лестницы к горизонту α = 60°, её масса m=15 кг. На лестнице на расстоянии а=1 м от её верхнего конца стоит человек массой М = 60 кг. С какой силой давит пол на нижний конец лестницы и как направлена эта сила?
 Y B β α A X
Y B β α A X
 Решение Запишем уравнения равновесия:
Решение Запишем уравнения равновесия:
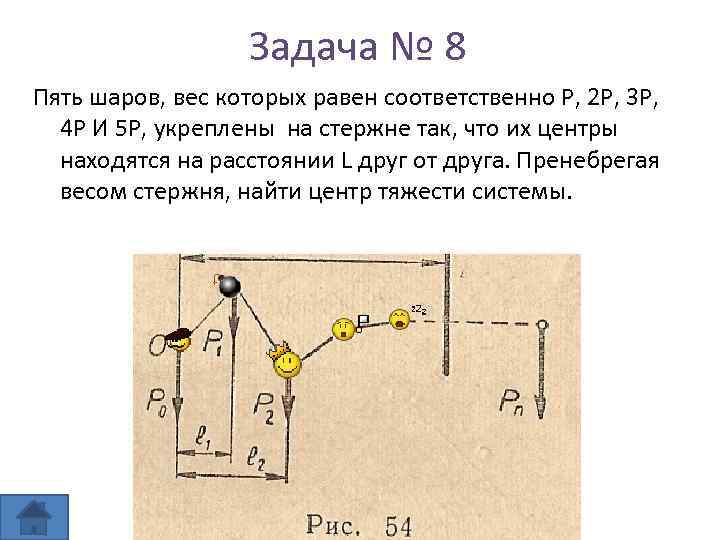 Задача № 8 Пять шаров, вес которых равен соответственно Р, 2 Р, 3 Р, 4 Р И 5 Р, укреплены на стержне так, что их центры находятся на расстоянии L друг от друга. Пренебрегая весом стержня, найти центр тяжести системы.
Задача № 8 Пять шаров, вес которых равен соответственно Р, 2 Р, 3 Р, 4 Р И 5 Р, укреплены на стержне так, что их центры находятся на расстоянии L друг от друга. Пренебрегая весом стержня, найти центр тяжести системы.
 Решение Искомое расстояние от точки О до силы F можно найти из уравнения моментов сил относительно точки О: Р 0*0+ P 1 l 1+…+ Pn ln – Fх=0 Где l 1, l 2 и т. д. –плечи сил относительно центра тяжести левого груза Р 0
Решение Искомое расстояние от точки О до силы F можно найти из уравнения моментов сил относительно точки О: Р 0*0+ P 1 l 1+…+ Pn ln – Fх=0 Где l 1, l 2 и т. д. –плечи сил относительно центра тяжести левого груза Р 0
 Решение Выразим х: Мы нашли основную формулу. Теперь можно решать задачу: F=P+2 P+3 P+4 P+5 P Плечи сил относительно точки О равны соответственно 0, l , 2 l , 3 l , 4 l. Определяем положение центра тяжести:
Решение Выразим х: Мы нашли основную формулу. Теперь можно решать задачу: F=P+2 P+3 P+4 P+5 P Плечи сил относительно точки О равны соответственно 0, l , 2 l , 3 l , 4 l. Определяем положение центра тяжести:
 Задача № 10 В системе, изображённой на рисунке, нить невесома и нерастяжима, блоки невесомы, трения нет. Массы грузов на концах нити равны m 1 и m 2, однородная доска массой m 3 лежит на горизонтальном столе так, что вертикальные участки нити, переброшенной через закреплённые на доске блоки, проходят вдоль её торцов. При каком условии доска при движении грузов будет оставаться в горизонтальном положении?
Задача № 10 В системе, изображённой на рисунке, нить невесома и нерастяжима, блоки невесомы, трения нет. Массы грузов на концах нити равны m 1 и m 2, однородная доска массой m 3 лежит на горизонтальном столе так, что вертикальные участки нити, переброшенной через закреплённые на доске блоки, проходят вдоль её торцов. При каком условии доска при движении грузов будет оставаться в горизонтальном положении?
 Решение: L=длина доски Т=сила натяжения (она одна и та же, т. к. нить не растяжима и блоки невесомы). доска покоится =>> Mmg относительно точки будет больше, чем MT, то есть (L/2) m 3 g>=TL, или T<=(m 3/2)g g>=TL Горизонтальных сил нет, так что при движении грузов, система остается неподвижной. OX: a 1= -a 2, т. к. нить нерастяжима Отсюда: Ответ:
Решение: L=длина доски Т=сила натяжения (она одна и та же, т. к. нить не растяжима и блоки невесомы). доска покоится =>> Mmg относительно точки будет больше, чем MT, то есть (L/2) m 3 g>=TL, или T<=(m 3/2)g g>=TL Горизонтальных сил нет, так что при движении грузов, система остается неподвижной. OX: a 1= -a 2, т. к. нить нерастяжима Отсюда: Ответ:
 Задача № 11 На горизонтальной плоскости на расстоянии А от закрепленной ступеньки лежит брусок. Высоты ступеньки и бруска одинаковы. На ребро бруска, параллельное краю ступеньки, опирается цилиндр, который может без трения вращаться вокруг оси O, прикрепленной к краю ступеньки. Массы бруска и цилиндра равны. Если , где —R радиус цилиндра, то брусок покоится, а если , то брусок скользит, не отрываясь от плоскости. Считая коэффициент трения между всеми трущимися поверхностями одинаковым, найти величину.
Задача № 11 На горизонтальной плоскости на расстоянии А от закрепленной ступеньки лежит брусок. Высоты ступеньки и бруска одинаковы. На ребро бруска, параллельное краю ступеньки, опирается цилиндр, который может без трения вращаться вокруг оси O, прикрепленной к краю ступеньки. Массы бруска и цилиндра равны. Если , где —R радиус цилиндра, то брусок покоится, а если , то брусок скользит, не отрываясь от плоскости. Считая коэффициент трения между всеми трущимися поверхностями одинаковым, найти величину.
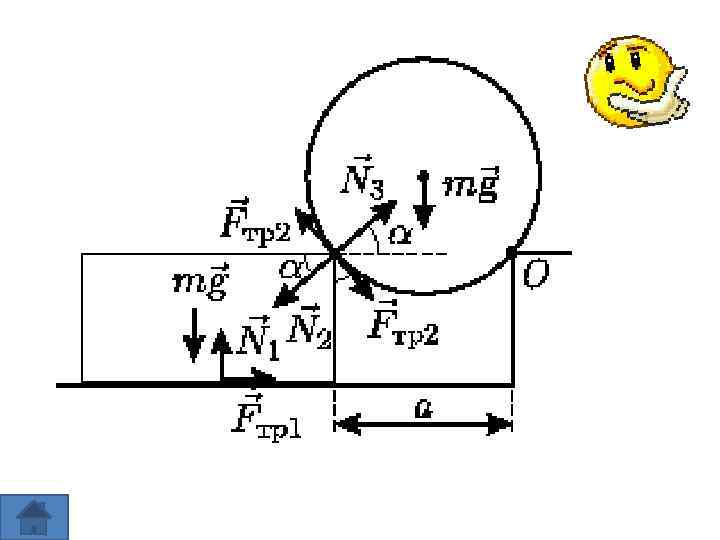
 Решение: При a<=21/2 R угол между нормальной составляющей силы брусок и горизонтом удовлетворяет условию: реакции цилиндра на Поскольку при этом брусок еще остается неподвижным относительно инерциальной системы отсчета, то согласно второму закону Ньютона: Согласно правилу моментов, записанному относительно оси, на которой закреплен цилиндр, условие его равновесия можно представить в виде: С учетом ранее полученных соотношений из этого уравнения следует: Берем лишь положительное значение:
Решение: При a<=21/2 R угол между нормальной составляющей силы брусок и горизонтом удовлетворяет условию: реакции цилиндра на Поскольку при этом брусок еще остается неподвижным относительно инерциальной системы отсчета, то согласно второму закону Ньютона: Согласно правилу моментов, записанному относительно оси, на которой закреплен цилиндр, условие его равновесия можно представить в виде: С учетом ранее полученных соотношений из этого уравнения следует: Берем лишь положительное значение:


