 ЭЛЕМЕНТЫ СИСТЕМЫ 1. 2. 3. 4. 5. СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 1. Назначение систем. Отличие? Тип элемента → уравнение, Yo=? описывающее его динамику и статику (дифференциальное), передаточная функция. Вид его статических и 2. Характер-ки систем. Зачем? Как? динамических характеристик. Собственные параметры (условно “постоянные во времени”) элемента. Способы соединений 3. Показатели качества работы элементов систем. Какие? Как узнать? (последовательное, параллельное, охват элемента местной обратной связью. Получение уравнений динамики элемента
ЭЛЕМЕНТЫ СИСТЕМЫ 1. 2. 3. 4. 5. СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 1. Назначение систем. Отличие? Тип элемента → уравнение, Yo=? описывающее его динамику и статику (дифференциальное), передаточная функция. Вид его статических и 2. Характер-ки систем. Зачем? Как? динамических характеристик. Собственные параметры (условно “постоянные во времени”) элемента. Способы соединений 3. Показатели качества работы элементов систем. Какие? Как узнать? (последовательное, параллельное, охват элемента местной обратной связью. Получение уравнений динамики элемента
 Разомкнутая система Задание, настройка системы / от оператора УПРАВЛЯЮЩЕЕ Yo Y УСТРОЙСТВО РЕГУЛЯТОР, ЭВМ + измерительная, преобразовательная, усилительная аппаратура, исполнительное устройство F Управляющее воздействие на объект Канал управления УПРАВЛЯЕМОЕ УСТРОЙСТВО (ОБЪЕКТ УПРАВЛЕНИЯ) U Информация о состоянии объекта Канал обратной связи F Yo F Y Yo ∆ Y Замкнутая система • Управляющее воздействие на объект - U • Информация о состоянии объекта - Y(y 1, y 2, . . . ) - по каналу обратной связи • Задание, настройка системы - Yo • Внешние помехи, нагрузка - F
Разомкнутая система Задание, настройка системы / от оператора УПРАВЛЯЮЩЕЕ Yo Y УСТРОЙСТВО РЕГУЛЯТОР, ЭВМ + измерительная, преобразовательная, усилительная аппаратура, исполнительное устройство F Управляющее воздействие на объект Канал управления УПРАВЛЯЕМОЕ УСТРОЙСТВО (ОБЪЕКТ УПРАВЛЕНИЯ) U Информация о состоянии объекта Канал обратной связи F Yo F Y Yo ∆ Y Замкнутая система • Управляющее воздействие на объект - U • Информация о состоянии объекта - Y(y 1, y 2, . . . ) - по каналу обратной связи • Задание, настройка системы - Yo • Внешние помехи, нагрузка - F
 НАЗНАЧЕНИЕ СИСТЕМ (ЗАДАЧА, РЕШАЕМАЯ АВТОМАТИЗАЦИЕЙ) • Цель (или задача) управления зависит от того, каким объектом будет управлять автоматическое управляющее устройство. 1 пример: объект управления - судовая энергетическая установка дизель-генератор. Эта установка предназначена для обеспечения энергией судового электрооборудования. Некоторые потребители требуют качественной энергии – стабильного напряжения и частоты (датчики, компьютеры, радиостанция, …). Для этой ситуации проектируют систему стабилизации контролируемых параметров объекта (или регулируемых координат объекта) – величины U и частоты f вырабатываемого напряжения, которые без системы управления сильно зависели бы от КОЛИЧЕСТВА подключенных потребителей - F.
НАЗНАЧЕНИЕ СИСТЕМ (ЗАДАЧА, РЕШАЕМАЯ АВТОМАТИЗАЦИЕЙ) • Цель (или задача) управления зависит от того, каким объектом будет управлять автоматическое управляющее устройство. 1 пример: объект управления - судовая энергетическая установка дизель-генератор. Эта установка предназначена для обеспечения энергией судового электрооборудования. Некоторые потребители требуют качественной энергии – стабильного напряжения и частоты (датчики, компьютеры, радиостанция, …). Для этой ситуации проектируют систему стабилизации контролируемых параметров объекта (или регулируемых координат объекта) – величины U и частоты f вырабатываемого напряжения, которые без системы управления сильно зависели бы от КОЛИЧЕСТВА подключенных потребителей - F.
 Статическая характеристика системы стабилизации (например, система стабилизации напряжения на шинах генератора) Регулируемые координаты /переменные параметры / Y U (вольт), f (Гц) Заданное значение Идеальная ситуация (Y=Y 0 ±ε) ? Реальная ситуация I ном. 2 I ном. 3 I ном. Нагрузка / Количество потребляемой энергии, I (A) ? ∆ = f(I) - статическая ошибка системы
Статическая характеристика системы стабилизации (например, система стабилизации напряжения на шинах генератора) Регулируемые координаты /переменные параметры / Y U (вольт), f (Гц) Заданное значение Идеальная ситуация (Y=Y 0 ±ε) ? Реальная ситуация I ном. 2 I ном. 3 I ном. Нагрузка / Количество потребляемой энергии, I (A) ? ∆ = f(I) - статическая ошибка системы
 Динамическая характеристика системы стабилизации (стабилизация напряжения генератора)
Динамическая характеристика системы стабилизации (стабилизация напряжения генератора)
 2 пример: объект управления - электродвигатель, предназначенный для поворота на заданный угол φо тяжелой массы, жестко закрепленной на его валу (руль, антенна, платформа подъемного крана, …). Заданный угол поворота вала двигателя может со временем меняться. φо (Y 0) – случайная функция времени. Некоторые объекты требуют высокой точности установки угла (антенны – сотые доли градуса, руль ± 0. 5 о). Для этой ситуации проектируют систему слежения за изменением задающего воздействия – заданного значения переменного параметра (или регулируемой координаты объекта – величины Y 0). .
2 пример: объект управления - электродвигатель, предназначенный для поворота на заданный угол φо тяжелой массы, жестко закрепленной на его валу (руль, антенна, платформа подъемного крана, …). Заданный угол поворота вала двигателя может со временем меняться. φо (Y 0) – случайная функция времени. Некоторые объекты требуют высокой точности установки угла (антенны – сотые доли градуса, руль ± 0. 5 о). Для этой ситуации проектируют систему слежения за изменением задающего воздействия – заданного значения переменного параметра (или регулируемой координаты объекта – величины Y 0). .
 Статическая и переходная характеристика системы слежения • Реакция (процесс изменения регулируемой координаты во времени) на задающее входное воздействие Входное воздействие Yo t t Регулируемая координата или переменный параметр (факт) Идеальная ситуация φ Динамическая ошибка φо 1 Статическая ошибка t φо, φ(t) Реальная ситуация φ = φо 1 Входное воздействие Yo φ (t) Статическая ошибка φо 1 Заданное значения φо Неустойчивая система t, сек t пп Характеристики, отражающие статику и динамику системы слежения. В чем различие интересов проектировщика при анализе статики систем стабилизации и слежения?
Статическая и переходная характеристика системы слежения • Реакция (процесс изменения регулируемой координаты во времени) на задающее входное воздействие Входное воздействие Yo t t Регулируемая координата или переменный параметр (факт) Идеальная ситуация φ Динамическая ошибка φо 1 Статическая ошибка t φо, φ(t) Реальная ситуация φ = φо 1 Входное воздействие Yo φ (t) Статическая ошибка φо 1 Заданное значения φо Неустойчивая система t, сек t пп Характеристики, отражающие статику и динамику системы слежения. В чем различие интересов проектировщика при анализе статики систем стабилизации и слежения?
 Реакция на гармонической воздействие
Реакция на гармонической воздействие
 20 lg(R) R – отношение амплитуд выходного и входного сигнала (на входе - гармоническое воздействие) – Ay / Ax (=1) Полоса пропускания частот 1 Желаемая 2 3 реальная lg f Частотная (динамическая) характеристика системы Почему интересуются частотной, а не переходным процессом?
20 lg(R) R – отношение амплитуд выходного и входного сигнала (на входе - гармоническое воздействие) – Ay / Ax (=1) Полоса пропускания частот 1 Желаемая 2 3 реальная lg f Частотная (динамическая) характеристика системы Почему интересуются частотной, а не переходным процессом?
 • Выбор и обоснование критериев эффективности (качества) процесса управления зависит от цели и, соответственно, от назначения системы. • Для системы стабилизации – жесткие требования на статические ошибки и менее жесткие на динамические показатели качества (динамические ошибки, длительность переходного процесса, колебательность). • Для системы слежения – более жесткие требования накладываются на динамику системы, особенно на полосу пропускания частот.
• Выбор и обоснование критериев эффективности (качества) процесса управления зависит от цели и, соответственно, от назначения системы. • Для системы стабилизации – жесткие требования на статические ошибки и менее жесткие на динамические показатели качества (динамические ошибки, длительность переходного процесса, колебательность). • Для системы слежения – более жесткие требования накладываются на динамику системы, особенно на полосу пропускания частот.
 ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ (частные - Х) • Надежность – оценивается по вероятности (количеству) отказов за единицу времени. • Устойчивость – способность возвращаться на заданный уровень ( или уровень Y 0 ± ε) после прекращения действия внешних помех (которые отклонили Y от из заданного состояния на величину δ > ε) за приемлемое время. Y F ε δ t t* t
ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ (частные - Х) • Надежность – оценивается по вероятности (количеству) отказов за единицу времени. • Устойчивость – способность возвращаться на заданный уровень ( или уровень Y 0 ± ε) после прекращения действия внешних помех (которые отклонили Y от из заданного состояния на величину δ > ε) за приемлемое время. Y F ε δ t t* t
 • Запас устойчивости – оценивается по вероятности перехода системы из устойчивой в неустойчивую, если какой-либо собственный параметр системы ( ki , Ti ) изменил своё значение. • Показатели переходного процесса – длительность переходного процесса – t пп, динамическая ошибка - δ, статическая ошибка - ε, количество колебаний за время переходного процесса - n. • Полоса пропускания частот ОБОБЩЕННЫЙ ПОКАЗАТЕЛЬ I =f (частные показатели Xi, весовые коэффициенты ci) I = c 1 X 1 +c 1 X 1 +…
• Запас устойчивости – оценивается по вероятности перехода системы из устойчивой в неустойчивую, если какой-либо собственный параметр системы ( ki , Ti ) изменил своё значение. • Показатели переходного процесса – длительность переходного процесса – t пп, динамическая ошибка - δ, статическая ошибка - ε, количество колебаний за время переходного процесса - n. • Полоса пропускания частот ОБОБЩЕННЫЙ ПОКАЗАТЕЛЬ I =f (частные показатели Xi, весовые коэффициенты ci) I = c 1 X 1 +c 1 X 1 +…
 ФУНКЦИОНАЛЬНАЯ СХЕМА СИСТЕМЫ АВТОМАТИКИ (ЛИНЕЙНАЯ СИСТЕМА) УСТРОЙСТВО УПРАВЛЕНИЯ (ЭВМ)
ФУНКЦИОНАЛЬНАЯ СХЕМА СИСТЕМЫ АВТОМАТИКИ (ЛИНЕЙНАЯ СИСТЕМА) УСТРОЙСТВО УПРАВЛЕНИЯ (ЭВМ)
 ДИСКРЕТНАЯ СИСТЕМА Внешние устройства для ЭВМ Внешние воздействия Объект управления Исполнительные устройства Выход на верхний уровень системы Пульт управления Датчик состояния 1 Датчик состояния 2 Датчик состояния 3 Канал управления Управляющая микро. ЭВМ или микроконтроллер Порты ввода/вывода сигналов Блок-схема модуля первого уровня информационно-управляющей системы
ДИСКРЕТНАЯ СИСТЕМА Внешние устройства для ЭВМ Внешние воздействия Объект управления Исполнительные устройства Выход на верхний уровень системы Пульт управления Датчик состояния 1 Датчик состояния 2 Датчик состояния 3 Канал управления Управляющая микро. ЭВМ или микроконтроллер Порты ввода/вывода сигналов Блок-схема модуля первого уровня информационно-управляющей системы
 СТРУКТУРНАЯ СХЕМА СИСТЕМЫ Y 0 Объект управления + датчик F W 0 (P) ? W 3(P) Y* U W 2(P) Исполнительное устройство W 4(P) Y ? W р (P) Алгоритм управления Автоматическое U* управляющее устройство W 1(P) усилитель W(p) → задает связь между входным и выходным сигналом, т. е. Выходная координата(p) = W(p) * Входная координата (p) У регулятора и объекта (как минимум) два входа один выход. Сколько можко составить передаточных функций W(p) = ?
СТРУКТУРНАЯ СХЕМА СИСТЕМЫ Y 0 Объект управления + датчик F W 0 (P) ? W 3(P) Y* U W 2(P) Исполнительное устройство W 4(P) Y ? W р (P) Алгоритм управления Автоматическое U* управляющее устройство W 1(P) усилитель W(p) → задает связь между входным и выходным сигналом, т. е. Выходная координата(p) = W(p) * Входная координата (p) У регулятора и объекта (как минимум) два входа один выход. Сколько можко составить передаточных функций W(p) = ?
 Передаточные функции по возмущающему и управляющему воздействиям F Y 0 + - ∆Y Wр Y W 1 W 2 U ОУ W 0 F + W 0 U W(p)эквив 1 Y Y* W 4 W(p) САУ = ? W 3 W(p)эквив 2 Входы Y 0 , F Выходы ∆Y, U, Y W(p) = ∆Y / Y 0 W(p) =∆Y / F W(p) = U / Y 0 W(p) = U / F W(p) = Y / Y 0 W(p) = Y / F Существует 6 вариантов передаточных функций. Как их найти?
Передаточные функции по возмущающему и управляющему воздействиям F Y 0 + - ∆Y Wр Y W 1 W 2 U ОУ W 0 F + W 0 U W(p)эквив 1 Y Y* W 4 W(p) САУ = ? W 3 W(p)эквив 2 Входы Y 0 , F Выходы ∆Y, U, Y W(p) = ∆Y / Y 0 W(p) =∆Y / F W(p) = U / Y 0 W(p) = U / F W(p) = Y / Y 0 W(p) = Y / F Существует 6 вариантов передаточных функций. Как их найти?
 Правило вывода W (p) - в числителе - передаточные функции звеньев, расположенных между заданными ( интересующими нас ) входом и выходом, в знаменателе - передаточные функции звеньев, расположенных между задающим входом и основным, выходным сигналом системы
Правило вывода W (p) - в числителе - передаточные функции звеньев, расположенных между заданными ( интересующими нас ) входом и выходом, в знаменателе - передаточные функции звеньев, расположенных между задающим входом и основным, выходным сигналом системы
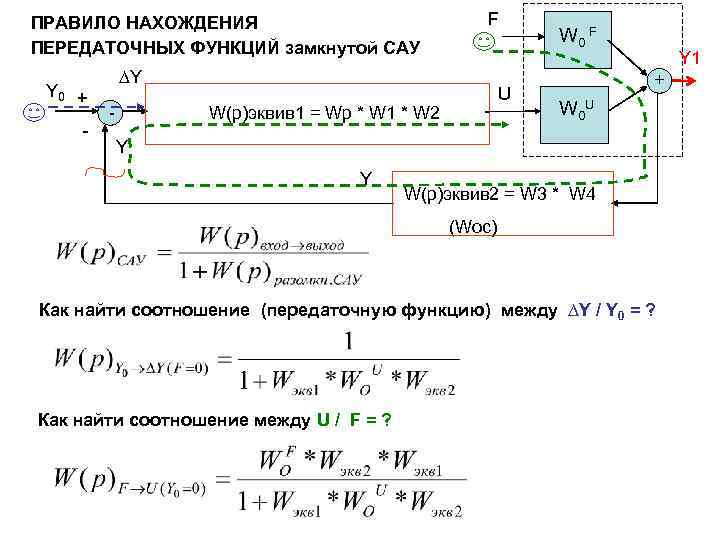 ПРАВИЛО НАХОЖДЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ замкнутой САУ Y 0 + - F ∆Y - U W(p)эквив 1 = Wp * W 1 * W 2 W 0 F Y 1 + W 0 U Y Y W(p)эквив 2 = W 3 * W 4 (Woc) Как найти соотношение (передаточную функцию) между ∆Y / Y 0 = ? Как найти соотношение между U / F = ?
ПРАВИЛО НАХОЖДЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ замкнутой САУ Y 0 + - F ∆Y - U W(p)эквив 1 = Wp * W 1 * W 2 W 0 F Y 1 + W 0 U Y Y W(p)эквив 2 = W 3 * W 4 (Woc) Как найти соотношение (передаточную функцию) между ∆Y / Y 0 = ? Как найти соотношение между U / F = ?

 Основная передаточная функция (между Y / Y 0 ) ПРАВИЛО ДЛЯ ВЫВОДА ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ СИСТЕМЫ Выходная координата * Знаменатель передаточной функции замкнутой системы = Входная координата * Числитель передаточной функции
Основная передаточная функция (между Y / Y 0 ) ПРАВИЛО ДЛЯ ВЫВОДА ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ СИСТЕМЫ Выходная координата * Знаменатель передаточной функции замкнутой системы = Входная координата * Числитель передаточной функции
 Передаточная функция разомкнутой системы Правило для вывода уравнения вынужденных движений системы При отсутствии вынуждающей силы имеем → Правило для вывода =0? уравнения собственных движений системы → Правило для вывода характеристического уравнения системы Неизменяемая часть уравнения Изменяемая часть
Передаточная функция разомкнутой системы Правило для вывода уравнения вынужденных движений системы При отсутствии вынуждающей силы имеем → Правило для вывода =0? уравнения собственных движений системы → Правило для вывода характеристического уравнения системы Неизменяемая часть уравнения Изменяемая часть

 Если в уравнение (*) подставить передаточные функции звеньев системы и положить то получим уравнение статики системы
Если в уравнение (*) подставить передаточные функции звеньев системы и положить то получим уравнение статики системы
 Таким образом, чтобы исследовать динамику и статику системы необходимо знать дифференциальные уравнения регулятора, объекта, измерительной, усилительгно-преобразовательной, исполнительной части системы и найти их передаточные функции ? известна
Таким образом, чтобы исследовать динамику и статику системы необходимо знать дифференциальные уравнения регулятора, объекта, измерительной, усилительгно-преобразовательной, исполнительной части системы и найти их передаточные функции ? известна
 АЛГОРИТМЫ УПРАВЛЕНИЯ Алгоритмы управления Непрерывные алгоритмы управления П, ПД, ПИД U = k 1 y , (y 0 – y) дискретные Релейный сложные логический ( if (A. >…) and (B>…). then U=… else if (A>…) and (…. ) then U=…) Если регулятор безинерционное звено, в противном случае в передаточную вводится инерционная составляющая
АЛГОРИТМЫ УПРАВЛЕНИЯ Алгоритмы управления Непрерывные алгоритмы управления П, ПД, ПИД U = k 1 y , (y 0 – y) дискретные Релейный сложные логический ( if (A. >…) and (B>…). then U=… else if (A>…) and (…. ) then U=…) Если регулятор безинерционное звено, в противном случае в передаточную вводится инерционная составляющая
 Таким образом, если выберем пропорциональный алгоритм управления, объект представим инерционным звеном, а исполнительно-усилительная часть инерционным интегрирующим, то будем иметь Характеристическое уравнение для исследования характера собственных движений системы примет вид
Таким образом, если выберем пропорциональный алгоритм управления, объект представим инерционным звеном, а исполнительно-усилительная часть инерционным интегрирующим, то будем иметь Характеристическое уравнение для исследования характера собственных движений системы примет вид
 • • Объект двигатель, Y(t) – скорость вращения вала ОС – датчик угловой скорости, безинерционный элемент Закон регулирования – пропорционально-дифференциальный Исполнительное устройство – инерционное звено 1 -го порядка
• • Объект двигатель, Y(t) – скорость вращения вала ОС – датчик угловой скорости, безинерционный элемент Закон регулирования – пропорционально-дифференциальный Исполнительное устройство – инерционное звено 1 -го порядка


 ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (все элементы описываются линейными дифференциальными уравнениями) (1 и 2 -ой пункты – в техническом задании) 1. Назначение систем автоматики, характеристики систем 2. Показатели качества систем 3. Функциональная схема САУ 4. Структурная схема САУ 5. Вывод уравнений системы
ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (все элементы описываются линейными дифференциальными уравнениями) (1 и 2 -ой пункты – в техническом задании) 1. Назначение систем автоматики, характеристики систем 2. Показатели качества систем 3. Функциональная схема САУ 4. Структурная схема САУ 5. Вывод уравнений системы


