Элементы симметрии правильных многогранников Подготовили ученицы 10 А

Элементы симметрии правильных многогранников. Подготовили ученицы 10 «А» класса Новикова Дарья и Соломатина Алена.

Многогранник — обычно замкнутая поверхность, составленная из многоугольников, но иногда так же называют тело, ограниченное этой поверхностью. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой его грани. Многогранник называется правильным, если его грани правильные многоугольники (т. е. такие, у которых все стороны и углы равны) и все многогранные углы при вершинах равны.

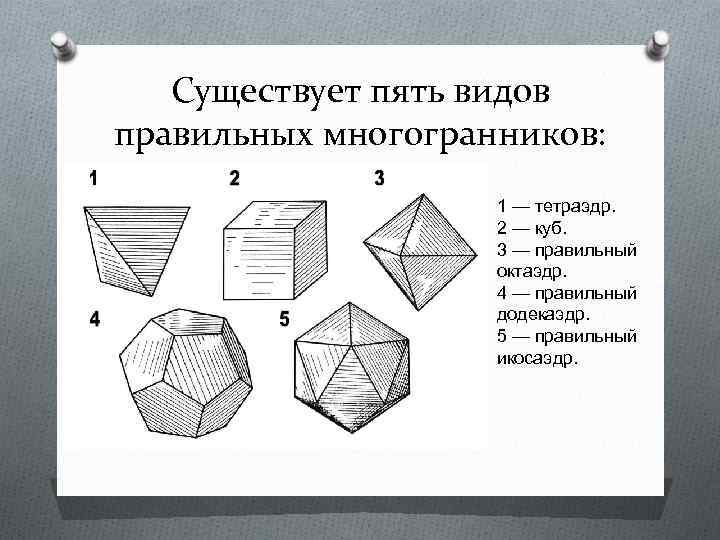Существует пять видов правильных многогранников: 1 — тетраэдр. 2 — куб. 3 — правильный октаэдр. 4 — правильный додекаэдр. 5 — правильный икосаэдр.

Тетраэдр — простейший Тетраэдр многогранник, гранями которого являются четыре треугольника. Тетраэдр имеет следующие характеристики: Тип грани – правильный треугольник; Число сторон у грани – 3; Общее число граней – 4; Число рёбер примыкающих к вершине – 3; Общее число вершин – 4; Общее число рёбер – 6.

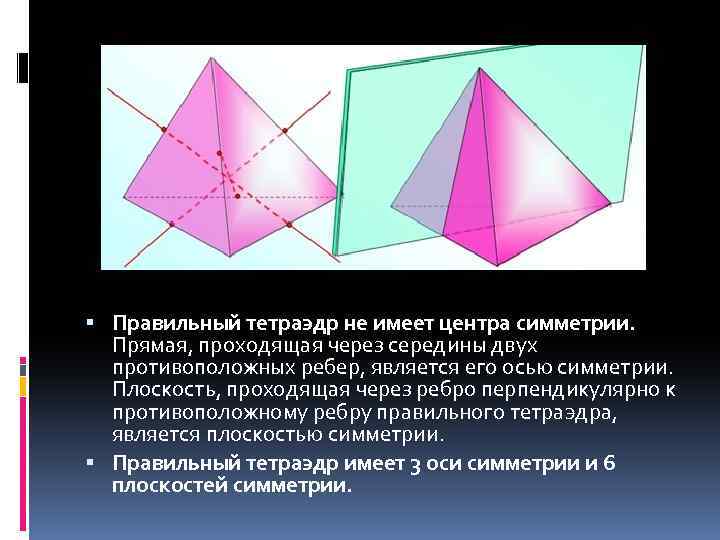Правильный тетраэдр не имеет центра симметрии. Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость, проходящая через ребро перпендикулярно к противоположному ребру правильного тетраэдра, является плоскостью симметрии. Правильный тетраэдр имеет 3 оси симметрии и 6 плоскостей симметрии.

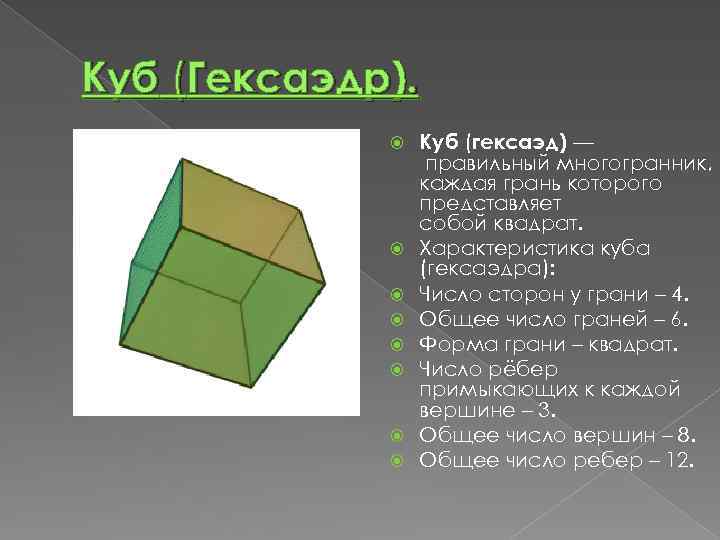Куб (Гексаэдр). Куб (гексаэд) — правильный многогранник, каждая грань которого представляет собой квадрат. Характеристика куба (гексаэдра): Число сторон у грани – 4. Общее число граней – 6. Форма грани – квадрат. Число рёбер примыкающих к каждой вершине – 3. Общее число вершин – 8. Общее число ребер – 12.

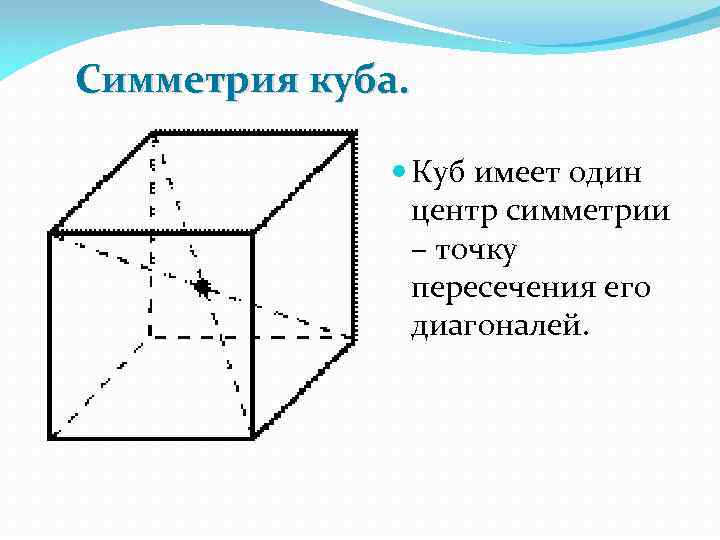Симметрия куба. Куб имеет один центр симметрии – точку пересечения его диагоналей.

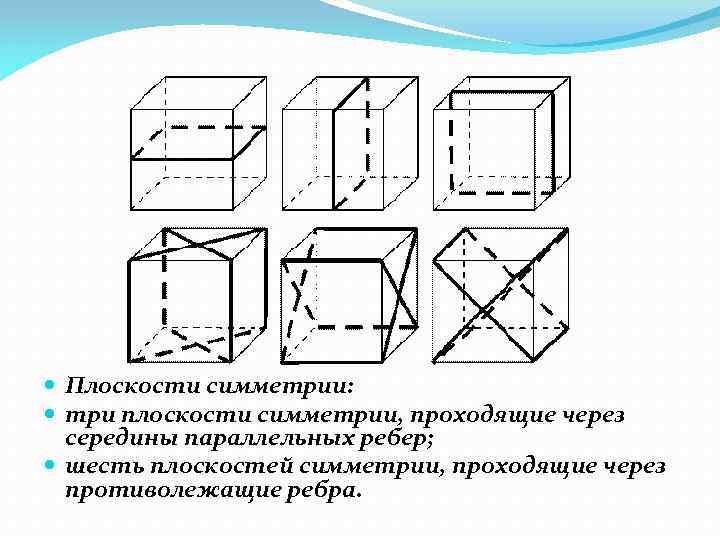Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер; шесть плоскостей симметрии, проходящие через противолежащие ребра.

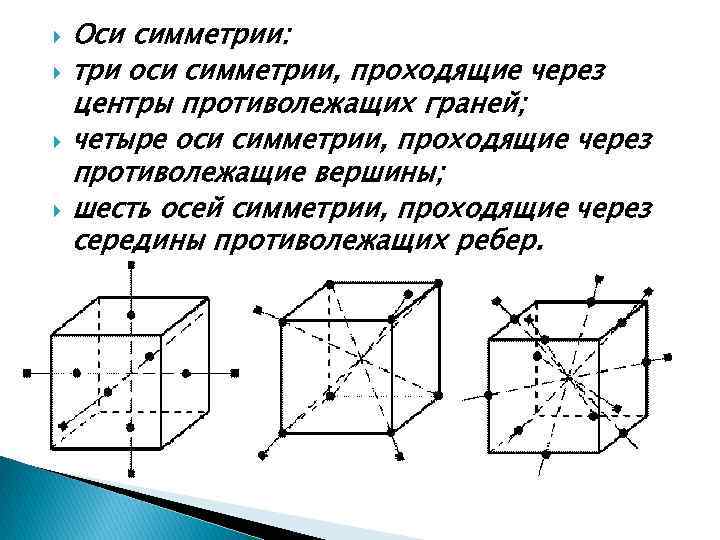Оси симметрии: три оси симметрии, проходящие через центры противолежащих граней; четыре оси симметрии, проходящие через противолежащие вершины; шесть осей симметрии, проходящие через середины противолежащих ребер.

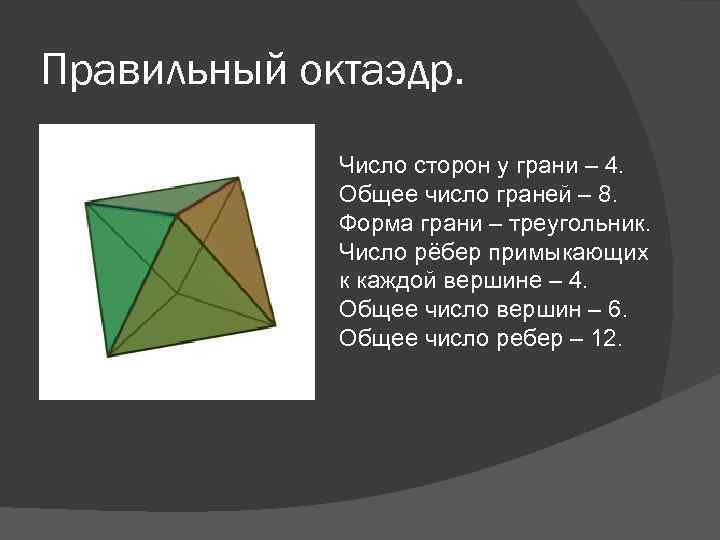Правильный октаэдр. Число сторон у грани – 4. Общее число граней – 8. Форма грани – треугольник. Число рёбер примыкающих к каждой вершине – 4. Общее число вершин – 6. Общее число ребер – 12.

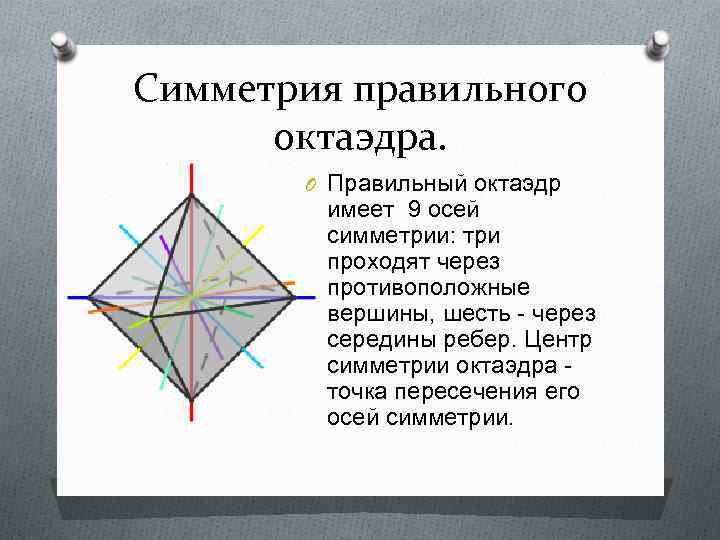Симметрия правильного октаэдра. O Правильный октаэдр имеет 9 осей симметрии: три проходят через противоположные вершины, шесть - через середины ребер. Центр симметрии октаэдра - точка пересечения его осей симметрии.

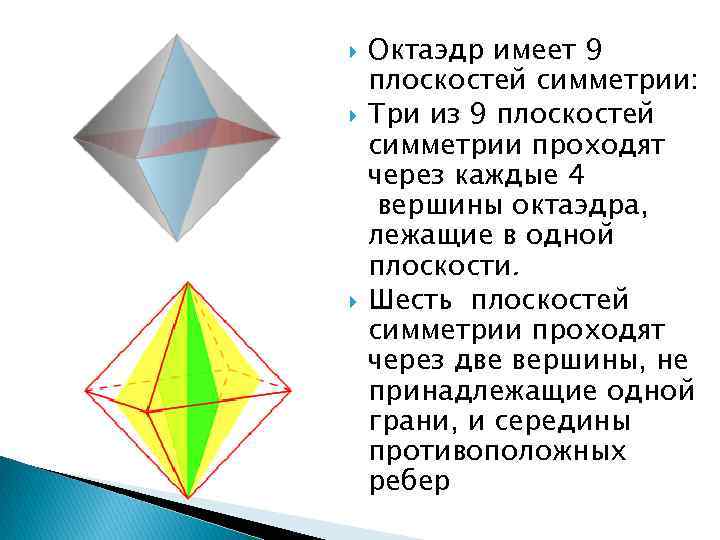Октаэдр имеет 9 плоскостей симметрии: Три из 9 плоскостей симметрии проходят через каждые 4 вершины октаэдра, лежащие в одной плоскости. Шесть плоскостей симметрии проходят через две вершины, не принадлежащие одной грани, и середины противоположных ребер

Правильный додекаэдр. Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.

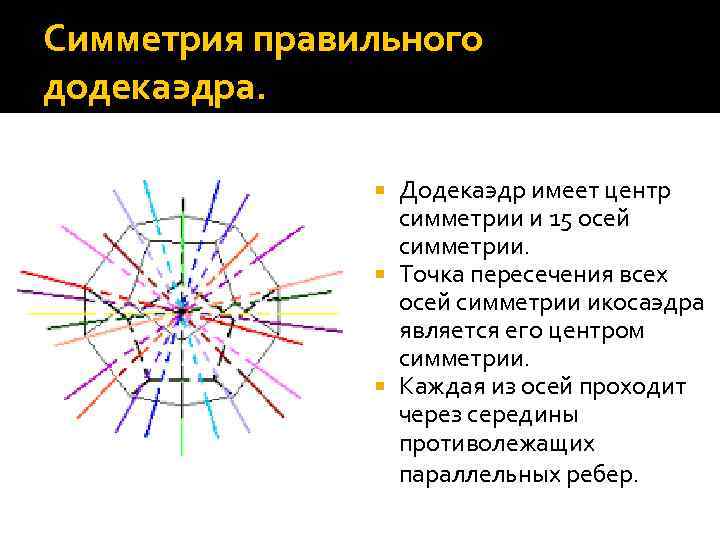Симметрия правильного додекаэдра. Додекаэдр имеет центр симметрии и 15 осей симметрии. Точка пересечения всех осей симметрии икосаэдра является его центром симметрии. Каждая из осей проходит через середины противолежащих параллельных ребер.

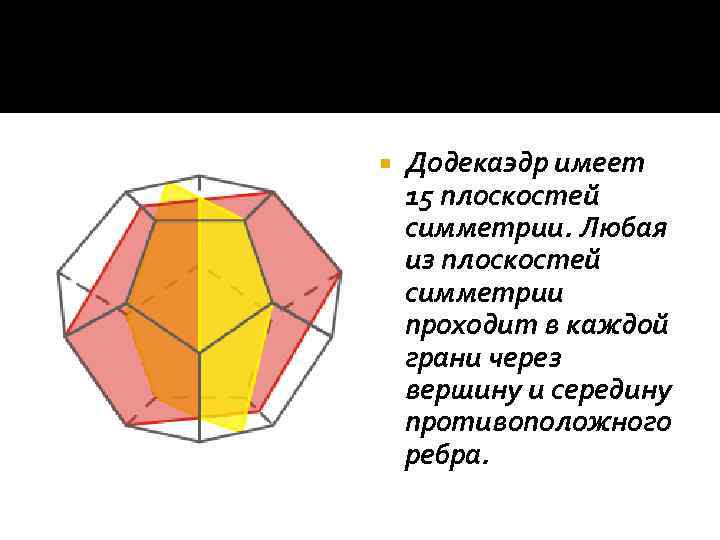Додекаэдр имеет 15 плоскостей симметрии. Любая из плоскостей симметрии проходит в каждой грани через вершину и середину противоположного ребра.

Правильный икосаэдр. Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.

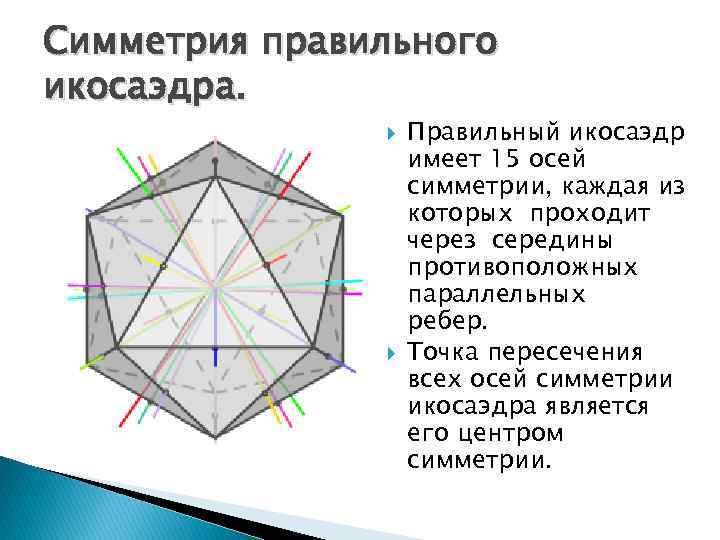Симметрия правильного икосаэдра. Правильный икосаэдр имеет 15 осей симметрии, каждая из которых проходит через середины противоположных параллельных ребер. Точка пересечения всех осей симметрии икосаэдра является его центром симметрии.

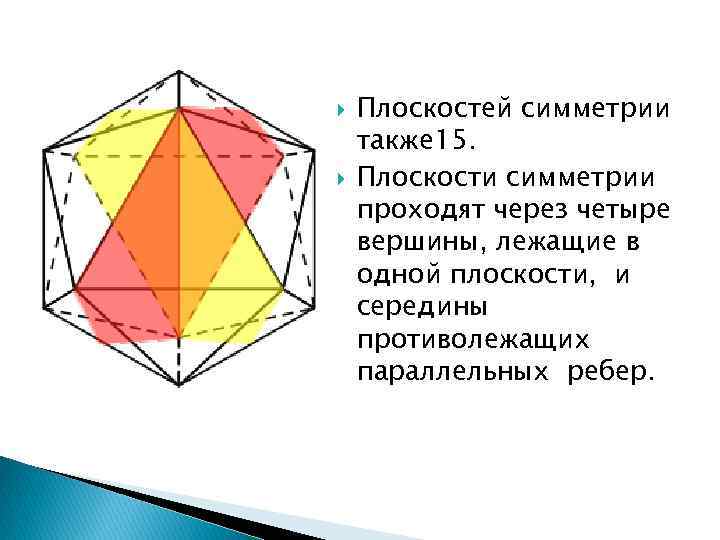Плоскостей симметрии также 15. Плоскости симметрии проходят через четыре вершины, лежащие в одной плоскости, и середины противолежащих параллельных ребер.