Элементы математической статистики








Элементы математической статистики.ppt
- Количество слайдов: 14
 Элементы математической статистики План лекции 1. Основные понятия математической статистики. 2. Характеристики положения. 3. Характеристики рассеивания.
Элементы математической статистики План лекции 1. Основные понятия математической статистики. 2. Характеристики положения. 3. Характеристики рассеивания.
 1. Основные понятия математической статистики Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Генеральной совокупностью называют совокупность всех возможных значений признака Х, т. е. всю совокупность объектов, подлежащих изучению. Выборочной совокупностью или выборкой называют совокупность случайно отобранных объектов. Выборочный метод состоит в том, что из генеральной совокупности берется выборка объема n и определяются числовые характеристики выборки, которые принимаются в качестве приближенных значений соответствующих характеристик генеральной совокупности.
1. Основные понятия математической статистики Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Генеральной совокупностью называют совокупность всех возможных значений признака Х, т. е. всю совокупность объектов, подлежащих изучению. Выборочной совокупностью или выборкой называют совокупность случайно отобранных объектов. Выборочный метод состоит в том, что из генеральной совокупности берется выборка объема n и определяются числовые характеристики выборки, которые принимаются в качестве приближенных значений соответствующих характеристик генеральной совокупности.
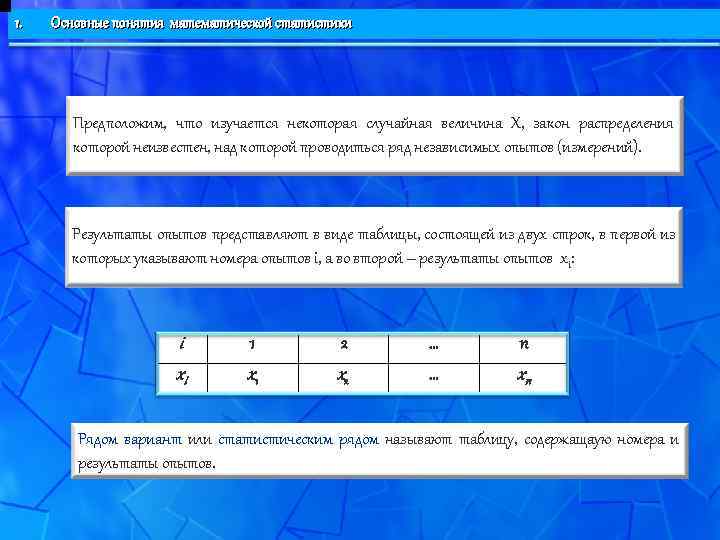
 1. Основные понятия математической статистики Предположим, что изучается некоторая случайная величина X, закон распределения которой неизвестен, над которой проводиться ряд независимых опытов (измерений). Результаты опытов представляют в виде таблицы, состоящей из двух строк, в первой из которых указывают номера опытов i, а во второй – результаты опытов xi: i 1 2 … n xi x 1 x 2 … xn Рядом вариант или статистическим рядом называют таблицу, содержащаую номера и результаты опытов.
1. Основные понятия математической статистики Предположим, что изучается некоторая случайная величина X, закон распределения которой неизвестен, над которой проводиться ряд независимых опытов (измерений). Результаты опытов представляют в виде таблицы, состоящей из двух строк, в первой из которых указывают номера опытов i, а во второй – результаты опытов xi: i 1 2 … n xi x 1 x 2 … xn Рядом вариант или статистическим рядом называют таблицу, содержащаую номера и результаты опытов.
 1. Основные понятия математической статистики Вариационным рядом выборки называют ранжированный в порядке возрастания или убывания ряд вариант хі с соответствующими частотами пі. Если в выборке объема n варианта х і встречается п і раз, то число n i называют частотой варианты xi: где k – число вариант xi Относительной частотой wi варианты xi называют отношение частоты ni варианты xi к объему выборки n: wi = ni/n, при этом
1. Основные понятия математической статистики Вариационным рядом выборки называют ранжированный в порядке возрастания или убывания ряд вариант хі с соответствующими частотами пі. Если в выборке объема n варианта х і встречается п і раз, то число n i называют частотой варианты xi: где k – число вариант xi Относительной частотой wi варианты xi называют отношение частоты ni варианты xi к объему выборки n: wi = ni/n, при этом
 1. Основные понятия математической статистики Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. xi x 1 x 2 … xn ni n 1 n 2 … nn xi x 1 x 2 … xn wi w 1 w 2 … wn При большом числе вариант целесообразно строить интервальный ряд распределения , для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала n i сумму частот вариант, попавших в i-й интервал.
1. Основные понятия математической статистики Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. xi x 1 x 2 … xn ni n 1 n 2 … nn xi x 1 x 2 … xn wi w 1 w 2 … wn При большом числе вариант целесообразно строить интервальный ряд распределения , для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала n i сумму частот вариант, попавших в i-й интервал.
 1. Основные понятия математической статистики Вариационный ряд называют дискретным , если две любые его варианты отличаются на постоянную величину, и – непрерывным ( интервальным ), если две любые его варианты отличаются на сколь угодно малую величину. Накопленной частотой m i данной варианты х і (или данного интервала ( х і-1 ; х і )) называют сумму всех частот, начиная с первой варианты (или интервала) до данной варианты (интервала) включительно. Для наглядности статистическое распределение выборки можно представить графически в виде полигона, гистограммы, куммулятивной кривой, огивы.
1. Основные понятия математической статистики Вариационный ряд называют дискретным , если две любые его варианты отличаются на постоянную величину, и – непрерывным ( интервальным ), если две любые его варианты отличаются на сколь угодно малую величину. Накопленной частотой m i данной варианты х і (или данного интервала ( х і-1 ; х і )) называют сумму всех частот, начиная с первой варианты (или интервала) до данной варианты (интервала) включительно. Для наглядности статистическое распределение выборки можно представить графически в виде полигона, гистограммы, куммулятивной кривой, огивы.
 1. Основные понятия математической статистики Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами (xi, ni). Полигоном относительных частот называют ломаную, отрезки которой соединяют точки с координатами (xi, wi). Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы длиной h , а высоты равны отношению (плотность частоты). Коммулятивной кривой называют ломаную, отрезки которой соединяют точки с координатами (xi, mi). Огивой называют ломаную, отрезки которой соединяют точки с координатами (mi, xi).
1. Основные понятия математической статистики Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами (xi, ni). Полигоном относительных частот называют ломаную, отрезки которой соединяют точки с координатами (xi, wi). Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы длиной h , а высоты равны отношению (плотность частоты). Коммулятивной кривой называют ломаную, отрезки которой соединяют точки с координатами (xi, mi). Огивой называют ломаную, отрезки которой соединяют точки с координатами (mi, xi).
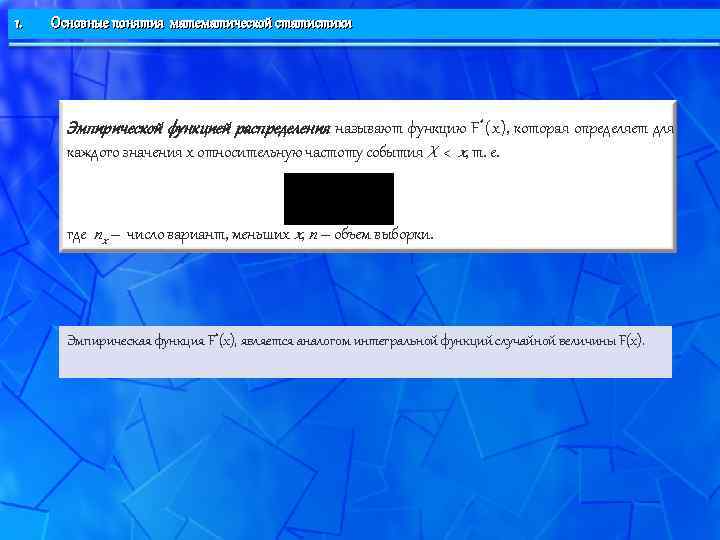
 1. Основные понятия математической статистики Эмпирической функцией распределения называют функцию F * (x), которая определяет для каждого значения x относительную частоту события X < x, т. е. где nx – число вариант, меньших x, n – объем выборки. Эмпирическая функция F*(x), является аналогом интегральной функций случайной величины F(x).
1. Основные понятия математической статистики Эмпирической функцией распределения называют функцию F * (x), которая определяет для каждого значения x относительную частоту события X < x, т. е. где nx – число вариант, меньших x, n – объем выборки. Эмпирическая функция F*(x), является аналогом интегральной функций случайной величины F(x).
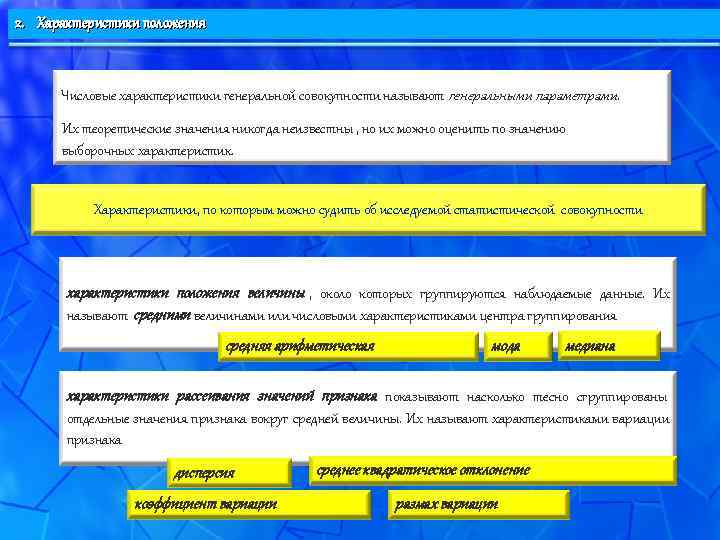
 2. Характеристики положения Числовые характеристики генеральной совокупности называют генеральными параметрами. Их теоретические значения никогда неизвестны , но их можно оценить по значению выборочных характеристик. Характеристики, по которым можно судить об исследуемой статистической совокупности характеристики положения величины , около которых группируются наблюдаемые данные. Их называют средними величинами или числовыми характеристиками центра группирования средняя арифметическая мода медиана характеристики рассеивания значений признака показывают насколько тесно сгруппированы отдельные значения признака вокруг средней величины. Их называют характеристиками вариации признака дисперсия среднее квадратическое отклонение коэффициент вариации размах вариации
2. Характеристики положения Числовые характеристики генеральной совокупности называют генеральными параметрами. Их теоретические значения никогда неизвестны , но их можно оценить по значению выборочных характеристик. Характеристики, по которым можно судить об исследуемой статистической совокупности характеристики положения величины , около которых группируются наблюдаемые данные. Их называют средними величинами или числовыми характеристиками центра группирования средняя арифметическая мода медиана характеристики рассеивания значений признака показывают насколько тесно сгруппированы отдельные значения признака вокруг средней величины. Их называют характеристиками вариации признака дисперсия среднее квадратическое отклонение коэффициент вариации размах вариации
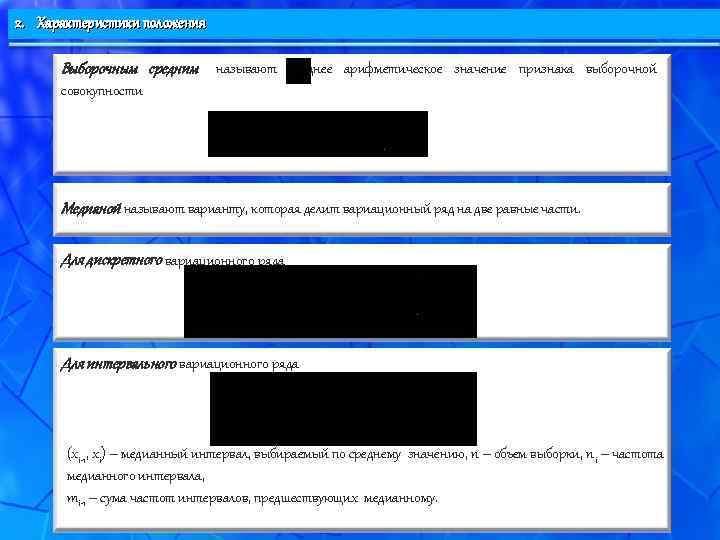
 2. Характеристики положения Выборочным средним называют среднее арифметическое значение признака выборочной совокупности Медианой называют варианту, которая делит вариационный ряд на две равные части. Для дискретного вариационного ряда Для интервального вариационного ряда (xi-1, xi) – медианный интервал, выбираемый по среднему значению, n – объем выборки, ni – частота медианного интервала, mi-1 – сума частот интервалов, предшествующих медианному.
2. Характеристики положения Выборочным средним называют среднее арифметическое значение признака выборочной совокупности Медианой называют варианту, которая делит вариационный ряд на две равные части. Для дискретного вариационного ряда Для интервального вариационного ряда (xi-1, xi) – медианный интервал, выбираемый по среднему значению, n – объем выборки, ni – частота медианного интервала, mi-1 – сума частот интервалов, предшествующих медианному.
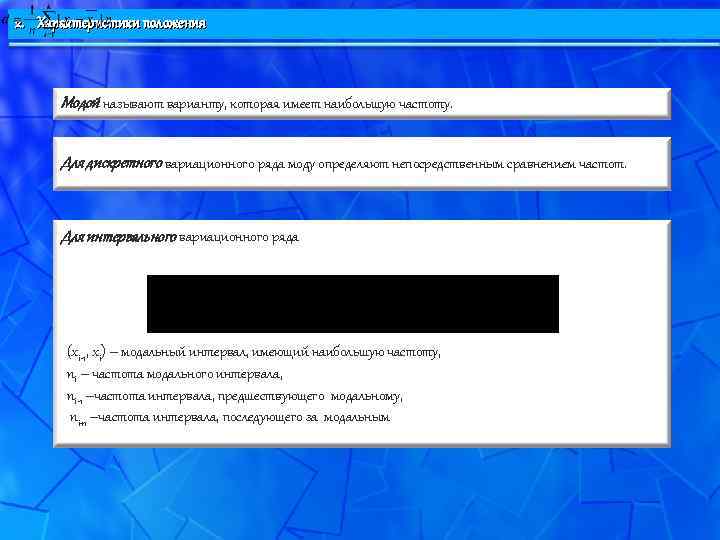
 2. Характеристики положения Модой называют варианту, которая имеет наибольшую частоту. Для дискретного вариационного ряда моду определяют непосредственным сравнением частот. Для интервального вариационного ряда (xi-1, xi) – модальный интервал, имеющий наибольшую частоту, ni – частота модального интервала, ni-1 –частота интервала, предшествующего модальному, ni+1 –частота интервала, последующего за модальным
2. Характеристики положения Модой называют варианту, которая имеет наибольшую частоту. Для дискретного вариационного ряда моду определяют непосредственным сравнением частот. Для интервального вариационного ряда (xi-1, xi) – модальный интервал, имеющий наибольшую частоту, ni – частота модального интервала, ni-1 –частота интервала, предшествующего модальному, ni+1 –частота интервала, последующего за модальным
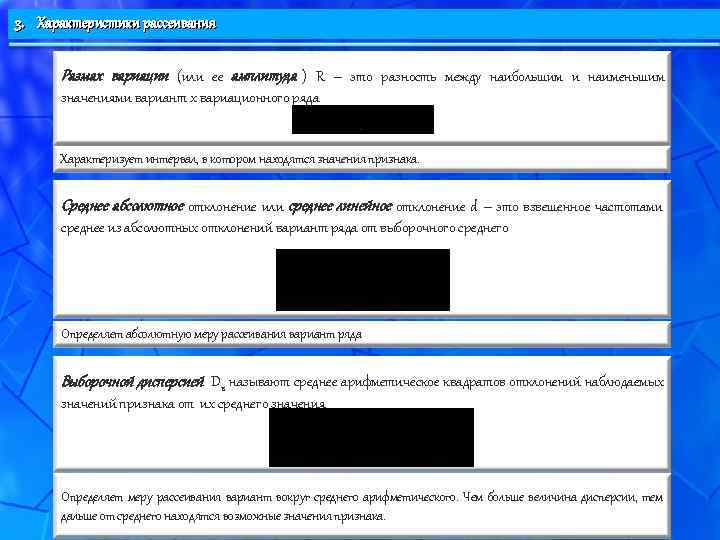
 3. Характеристики рассеивания Размах вариации (или ее амплитуда ) R – это разность между наибольшим и наименьшим значениями вариант x вариационного ряда Характеризует интервал, в котором находятся значения признака. Среднее абсолютное отклонение или среднее линейное отклонение d – это взвешенное частотами среднее из абсолютных отклонений вариант ряда от выборочного среднего Определяет абсолютную меру рассеивания вариант ряда Выборочной дисперсией D в называют среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения Определяет меру рассеивания вариант вокруг среднего арифметического. Чем больше величина дисперсии, тем дальше от среднего находятся возможные значения признака.
3. Характеристики рассеивания Размах вариации (или ее амплитуда ) R – это разность между наибольшим и наименьшим значениями вариант x вариационного ряда Характеризует интервал, в котором находятся значения признака. Среднее абсолютное отклонение или среднее линейное отклонение d – это взвешенное частотами среднее из абсолютных отклонений вариант ряда от выборочного среднего Определяет абсолютную меру рассеивания вариант ряда Выборочной дисперсией D в называют среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения Определяет меру рассеивания вариант вокруг среднего арифметического. Чем больше величина дисперсии, тем дальше от среднего находятся возможные значения признака.
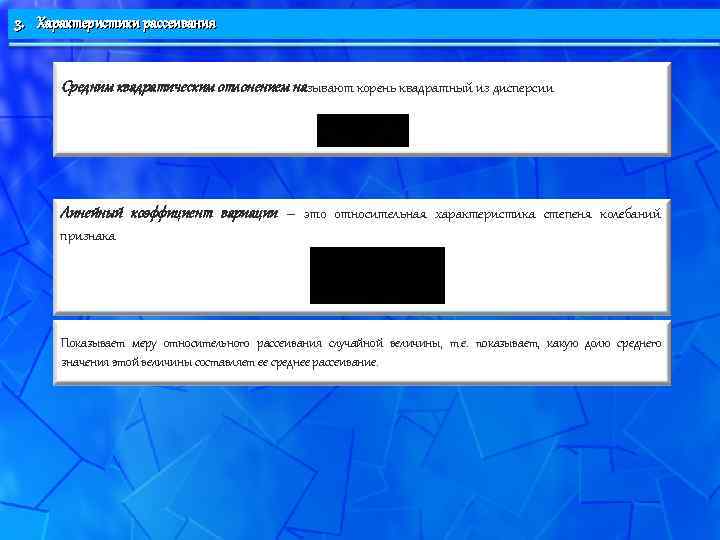
 3. Характеристики рассеивания Средним квадратическим отлонением называют корень квадратный из дисперсии Линейный коэффициент вариации – это относительная характеристика степеня колебаний признака Показывает меру относительного рассеивания случайной величины, т. е. показывает, какую долю среднего значения этой величины составляет ее среднее рассеивание.
3. Характеристики рассеивания Средним квадратическим отлонением называют корень квадратный из дисперсии Линейный коэффициент вариации – это относительная характеристика степеня колебаний признака Показывает меру относительного рассеивания случайной величины, т. е. показывает, какую долю среднего значения этой величины составляет ее среднее рассеивание.
 БЛАГОДАРЮ ЗА ВНИМАНИЕ!
БЛАГОДАРЮ ЗА ВНИМАНИЕ!

