Элементы математической логики Логика o Математическая логика

Элементы математической логики

Логика o Математическая логика выделилась из логики o Логика – аналитическая теория искусства рассуждения, целью которой является систематизация и формализация принципов правильного рассуждения o Ее истоки - учение Аристотеля о силлогических умозаключениях o Силлогические умозаключения - это умозаключения от общего к частному, например: Все хищники питаются мясом. Волк – хищник. Следовательно волк питается мясом

Математическая логика o В средние века на основе логики возникает математическая логика – это логика, основанная не на содержательной стороне высказываний, а на синтаксических категориях и их операционных связях. o Математическая логика внешне отличается от обычной тем, что она широко пользуется языком математических и логических знаков, исходя из того, что в принципе они могут заменить слова обычного языка и принятые в обычных живых языках способы объединения слов в

Математическая логика o Вследствие формализации логики возникла идея о том, что записав все исходные допущения на языке специальных математических знаков можно заменить рассуждение вычислением (1847 г. , англ. математик Джордж Буль, алгебра логики – Булева алгебра) o Существуют различные логические исчисления, такие как пропозициональное исчисление (исчисление высказываний), исчисление предикатов, ситуационное исчисление, многозначные логики, нечеткие логики и т. д.

Логика высказываний o Высказывание – это любое утверждение, относительно которого в данный момент можно однозначно сказать, что оно является истинным или ложным

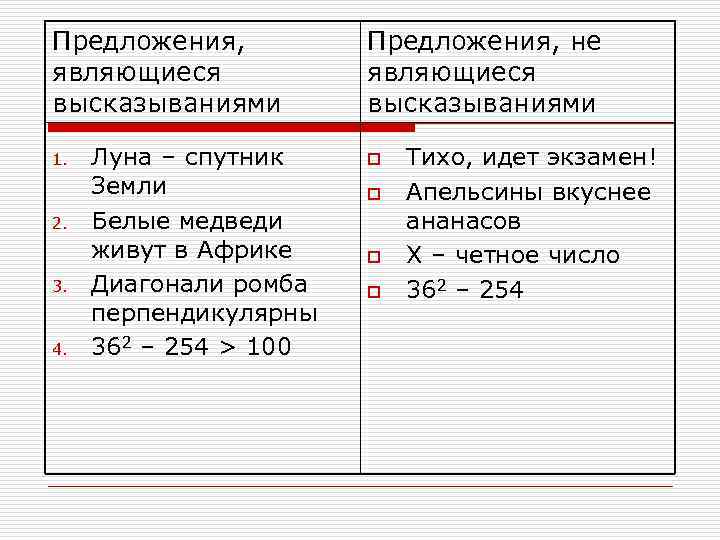Предложения, не являющиеся высказываниями высказываниями 1. Луна – спутник o Тихо, идет экзамен! Земли o Апельсины вкуснее 2. Белые медведи ананасов живут в Африке o Х – четное число 3. Диагонали ромба o 362 – 254 перпендикулярны 4. 362 – 254 > 100

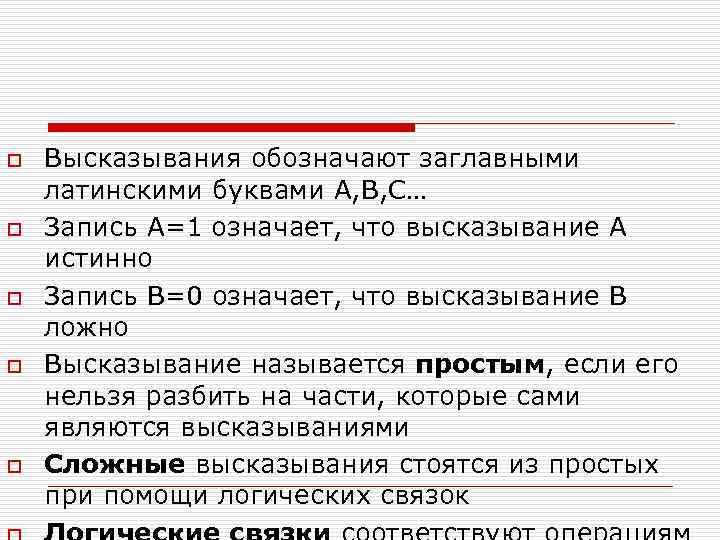o Высказывания обозначают заглавными латинскими буквами A, B, C… o Запись А=1 означает, что высказывание А истинно o Запись В=0 означает, что высказывание В ложно o Высказывание называется простым, если его нельзя разбить на части, которые сами являются высказываниями o Сложные высказывания стоятся из простых при помощи логических связок

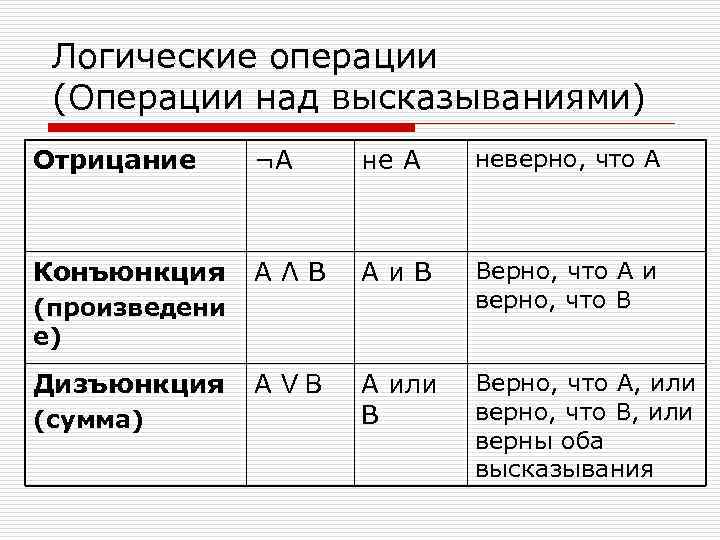Логические операции (Операции над высказываниями) Отрицание ¬А неверно, что А Конъюнкция AΛB Aи. В Верно, что А и (произведени верно, что В е) Дизъюнкция АVВ А или Верно, что А, или (сумма) В верно, что В, или верны оба высказывания

Логические операции (Операции над высказываниями) Исключающ Или А, Верно что-то ая или В одно: или А, или дизъюнкция В Импликация А→В Если А, Если верно, что (следование) то В; А, то верно, что В (Из А (А - условие следует В – следствие) В) Эквивалент- А↔В А Верно, что А ность равнос тогда и только (равенство) ильно В тогда, когда верно, что В

Задача 1 Пусть А= «шумел камыш» , В= «деревья гнулись» Примените к этим высказываниям все 6 логических операций, запишите получившиеся предложения

Задача 2. Записать сложные высказывания в формализованном виде 1. «Я на свете всех милее и румяней и белее» 2. «Студенты готовятся к экзаменам по конспектам или по учебникам» 3. «Сегодня вечером я пойду в кино или в театр» 4. «Если пойдет дождь, то я либо возьму зонт, либо надену плащ» 5. «Если мистер Джонс счастлив, то миссис Джонс несчастлива и если мистер Джонс несчастлив, то миссис Джонс счастлива» 6. Карпов или математик или шахматист или и математик и шахматист одновременно

Задача 3 Пусть P= «Сегодня идет дождь» Q= «Сегодня хорошая погода» R= «Сегодня идет снег» S= «Вчера было пасмурно» Расшифруйте: Q → (¬(P Λ R) S → (P V R) Q V (¬(S → P)) S Λ ((P V R) → (¬Q))

Таблица истинности o Поскольку высказывания рассматривают только с точки зрения их логического значения (истина или ложь, 1 или 0), то и логические операции рассматриваются как средство вычисления логического значения сложного высказывания по логическим значениям составляющих его простых высказываний o Зависимость значения истинности сложного высказывания от истинности составляющих его простых высказываний можно выразить с помощью таблицы, называемой таблицей истинности

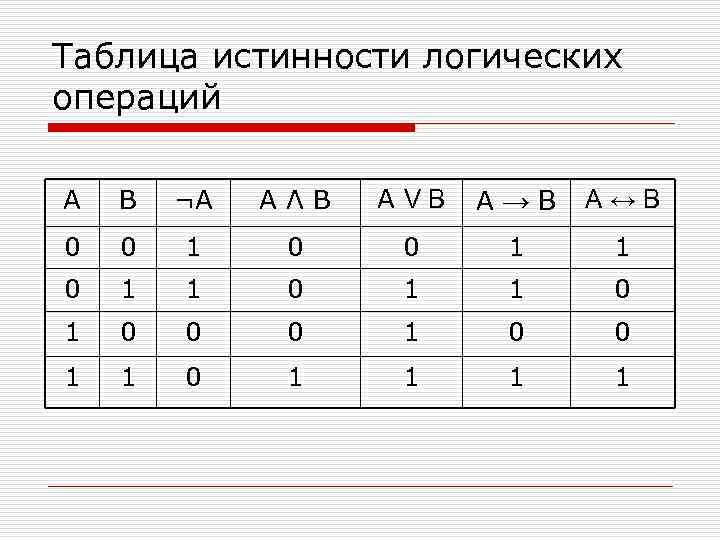Таблица истинности логических операций А В ¬А AΛB АVВ А→В А↔В 0 0 1 0 0 1 1 0 1 1 0 1 0 0 0 1 1 0 1 1

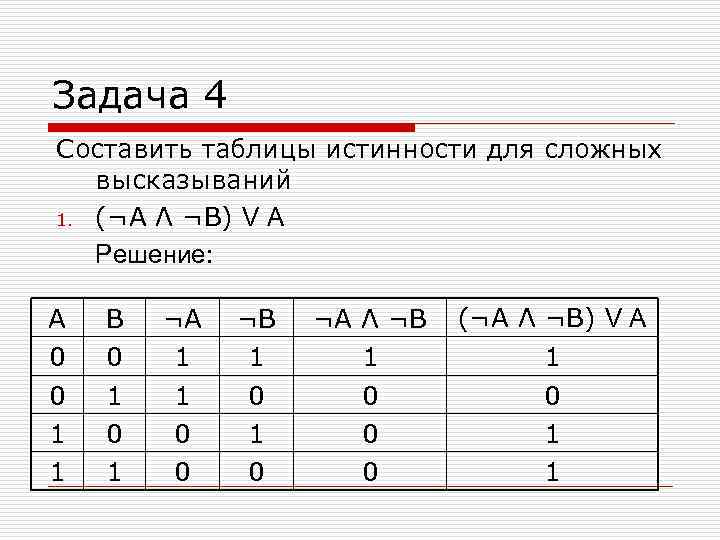Задача 4 Составить таблицы истинности для сложных высказываний 1. (¬A Λ ¬B) V A Решение: A B ¬A ¬B ¬A Λ ¬B (¬A Λ ¬B) V A 0 0 1 1 0 0 0 1 0 0 1 1 1 0 0 0 1

Задача 4 (продолжение) 2. ¬(¬A Λ ¬B) V A 3. (¬A → B) V (A Λ B) 4. (¬A Λ B) V (A Λ B) 5. (¬A V ¬B) 6. (¬A V ¬B)

Свойства логических операций 1. Закон двойного отрицания ¬(¬А) ↔ А 2. Коммутативность конъюнкции AΛB↔ВΛА 3. Коммутативность дизъюнкции AVB↔ВVА 4. Ассоциативность конъюнкции A Λ (B Λ С) ↔ (A Λ B) Λ С 5. Ассоциативность дизъюнкции A V (B V С) ↔ (A V B) V С

Свойства логических операций 6. Дистрибутивность дизъюнкции относительно конъюнкции A V (B Λ С) ↔ (A V B) Λ (А V С) 7. Дистрибутивность конъюнкции относительно дизъюнкции A Λ (B V С) ↔ (A Λ B) V (А Λ С) 8. Идемпотентность дизъюнкции AVА↔А 9. Идемпотентность конъюнкции AΛА↔А 10. Закон поглощения для дизъюнкции A V (А Λ В) ↔ A 11. Закон поглощения для конъюнкции A Λ (А V В) ↔ A

Свойства логических операций 12. Операции с инверсией A Λ ¬А ↔ 0 A V ¬А ↔ 1 13. Операции с константой AΛ 1↔А AV 1↔ 1 AΛ 0↔ 0 AV 0↔А 14. Законы Моргана ¬ (A V В) ↔ (¬А Λ ¬В) ¬ (A Λ В) ↔ (¬А V ¬В) 15. Контрапозиции (A → B) ↔ (¬В → ¬ А)

Свойства логических операций 16. Замена эквиваленции (A ↔ B) ↔ (A → B) Λ (В → А) 17. Замена импликации (A → B) ↔ (¬ А V В) 18. Замена дизъюнкции (A V B) ↔ ¬ (¬ А Λ ¬В) 19. Транзитивность эквивалентности (A ↔ B) Λ (В ↔ С) → (A ↔ С) 20. Правило силлогизма (транзитивность импликации (A → B) Λ (В → С) → (A → С) Докажите законы логики высказываний с помощью таблиц истинности

Преобразования логических выражений o С помощью законов можно проводить преобразования логических выражений точно так же, как в обычной алгебре. o Например, (17) (1) (3) (17) (¬B→¬ А) ↔ (¬(¬ B) V ¬ А) ↔ ( B V ¬ А) ↔ (¬ А V B) ↔ (А→В) То есть (¬B→¬ А) ↔ (А→В)

Задача 5. o Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники были на синем «Бьюике» , Джонс сказал, что это был чѐрный «Крайслер» , а Смит утверждал, что это был «Форд Мустанг» , но ни в коем случае не синий. Стало известно, что желая запутать следствие, каждый из них указал правильно либо только марку машины, либо еѐ цвет. Какого цвета был автомобиль и какой марки?

Решение. (A V B) Λ (C V D) Λ (¬A V Е) ↔ ((AΛC) V (AΛD) V (BΛC) V (BΛD)) Λ (¬A V Е) ↔ (AΛCΛ(¬A)) V (AΛDΛ(¬A)) V (BΛCΛ(¬A)) V (BΛDΛ(¬A)) V ((AΛCΛЕ) V (AΛDΛЕ) V (BΛCΛЕ) V (BΛDΛЕ) Дизъюнкция восьми высказываний может быть истинным высказыванием только в том случае, когда хотя бы одно из них истинно. Из определения высказываний сразу же следует, что все высказывания, кроме третьего ложны. Значит, истинно третье высказывание Ответ: чѐрный «Бьюик» .

Задача 6. «Вернувшись домой, Мегрэ позвонил на набережную Орфевр. – Говорит Мегрэ. Есть новости? – Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжѐт. Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи. Инспектор Люка попросил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжѐт. Затем звонила … – Всѐ, спасибо. Этого достаточно. – Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжѐт. Теперь он знал

Задача 6. Рассмотрите следующие высказывания: А= «Франсуа был пьян» ; В= «Этьен убийца» ; С= «Франсуа лжѐт» ; D= «убийство произошло после полуночи» . Используя логические операции, запишите высказывания инспекторов. Составьте конъюнкцию этих высказываний и упростите ее. Какой вывод сделал комиссар Мегрэ?

Головоломка Эйнштейна 1. Есть пять домов разного цвета: красный, зеленый, белый, желтый и синий. 2. Каждый населен человеком разной национальности: немец, швед, датчанин, норвежец и англичанин. 3. Каждый из них пьет один вид напитков, курит одну марку сигарет и держит одно домашнее животное. 4. Каждый из них уникален в пределах группы (напиток, марка сигарет, животное не повторяется!). Вопрос: кто держит рыбку?

Головоломка Эйнштейна 1. Англичанин живет в красном доме. 2. Швед держит собаку. 3. Датчанин пьет чай. 4. Зеленый дом - налево от белого. 5. Жилец зеленого дома пьет кофе. 6. Курильщик Pall Mall держит птичку. 7. Жилец дома, находящегося в середине, пьет молоко. 8. Жилец желтого дома курит Dunhill. 9. Норвежец живет в первом доме. 10. Курильщик Marlbore живет рядом с владельцем кота. 11. Владелец лошади живет рядом с курильщиком Dunhill. 12. Курильщик Winfield пьет пиво. 13. Дом Норвежца - рядом с синим домом.

o Самостоятельно № 33 -36, стр 36,