Элементы кристаллографии Структура кристалла и его геометрическая модель

Элементы кристаллографии. Структура кристалла и его геометрическая модель – пространственная решетка. Анизотропия и симметрия физиче ских свойств — характерная особен ность кристаллов, обусловленная закономерностью и симметрией их внут реннего строения. В кристаллах структурные единицы (атомы, ионы или молекулы) образуют бесконечные сетки или пространственные каркасы, которые характеризуются трехмерно периодическим расположением. Под кристаллической структурой обычно подразумевают порядок расположения структурных единиц в пространстве. 1

Кристаллическая структура – имеется дальний порядок в расположении атомов. Аморфная структура – дальнего порядка нет. 2

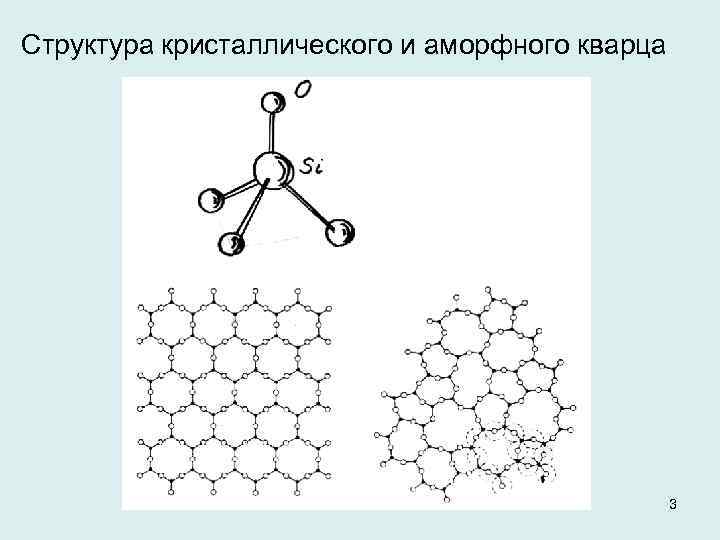Структура кристаллического и аморфного кварца 3

Если соединить в кристалле все периодически повторяемые структурные единицы одного сорта в трех измерениях, можно построить объемный периодический каркас, ко торый называют кристаллической решеткой. Кристаллическая решетка формируется в результате периодического повторения в пространстве по всем координатам без каких либо разрывов и пропусков маленького параллелепипеда повторяемости элементарной ячейки. Элементарную ячейку пространственной кристаллической решетки оп ределяют с помощью трех базисных векторов, обычно обозначаемых как а, b и с. 4

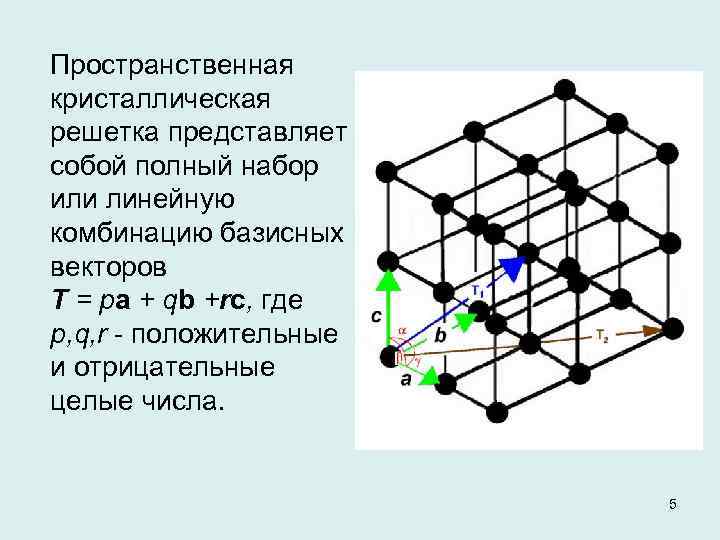Пространственная кристаллическая решетка представляет собой полный набор или линейную комбинацию базисных векторов T = рa + qb +rc, где р, q, r положительные и отрицательные целые числа. 5

«Кристаллическая решетка» строение идеального кристалла правиль ного трехмерно периодического расположения его структурных единиц в пространстве. «Кристаллическая структура» характеризует реальный кристалл, принимая во внимание его дефектную структуру.

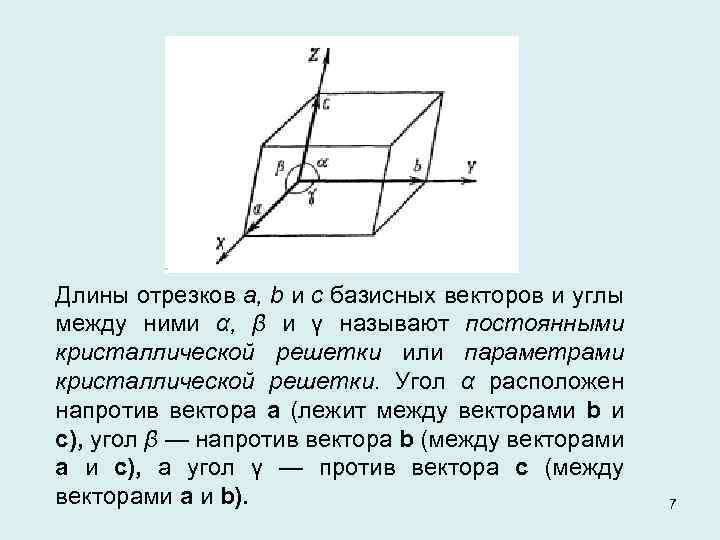Длины отрезков а, b и с базисных векторов и углы между ними α, β и γ называют постоянными кристаллической решетки или параметрами кристаллической решетки. Угол α расположен напротив вектора а (лежит между векторами b и с), угол β — напротив вектора b (между векторами а и с), а угол γ — против вектора с (между векторами а и b). 7

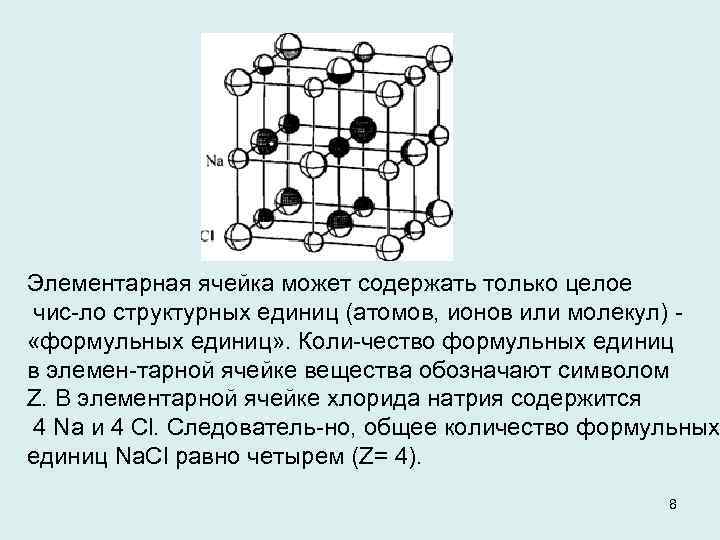Элементарная ячейка может содержать только целое чис ло структурных единиц (атомов, ионов или молекул) «формульных единиц» . Коли чество формульных единиц в элемен тарной ячейке вещества обозначают символом Z. В элементарной ячейке хлорида натрия содержится 4 Na и 4 Сl. Cледователь но, общее количество формульных единиц Na. Сl равно четырем (Z= 4). 8

Сингонии и системы координат. Кристаллы, для ко торых одинакова симметрия элементарных ячеек и одинако ва система координат, объединяются в сингонии. Всего существует 7 сингоний: кубическая, тетрагональная, тригональная и гексагональная, тригональная (ромбоэдрическая), ромбическая, моноклинная, триклинная. Классификация кристаллов по сингониям определяется выбором элементарной ячейки кристалла. 9

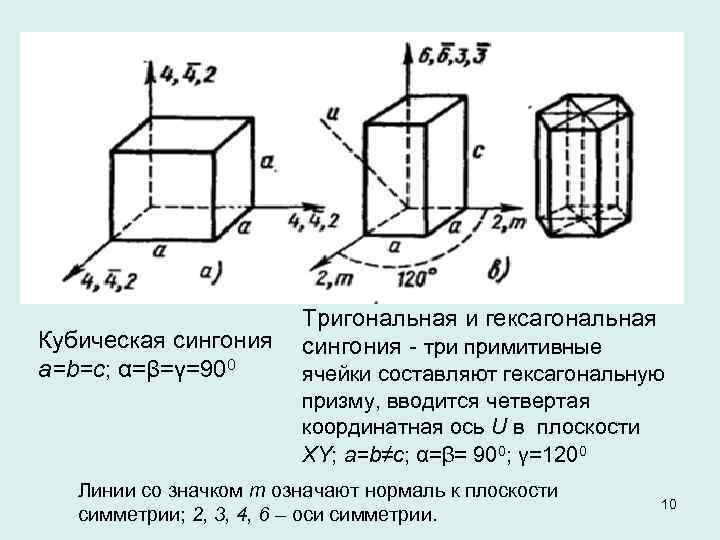Кубическая сингония a=b=c; α=β=γ=900 Тригональная и гексагональная сингония три примитивные ячейки составляют гексагональную призму, вводится четвертая координатная ось U в плоскости XY; a=b≠c; α=β= 900; γ=1200 Линии со значком m означают нормаль к плоскости симметрии; 2, 3, 4, 6 – оси симметрии. 10

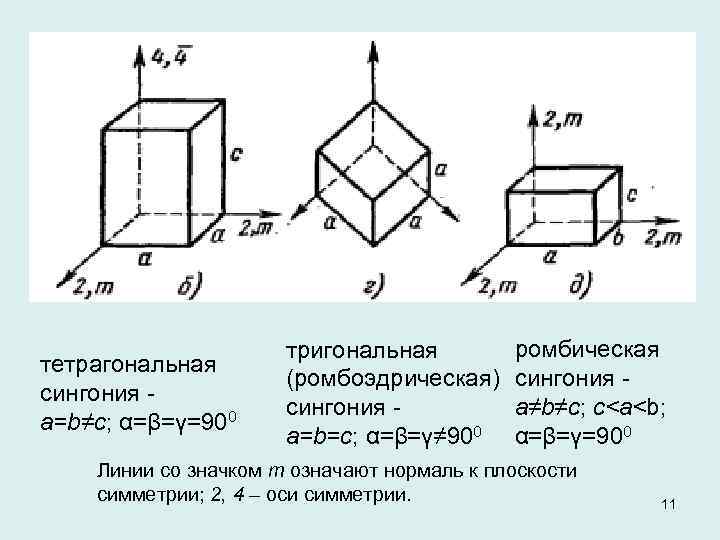тетрагональная сингония a=b≠c; α=β=γ=900 тригональная (ромбоэдрическая) сингония a=b=c; α=β=γ≠ 900 ромбическая сингония a≠b≠c; c

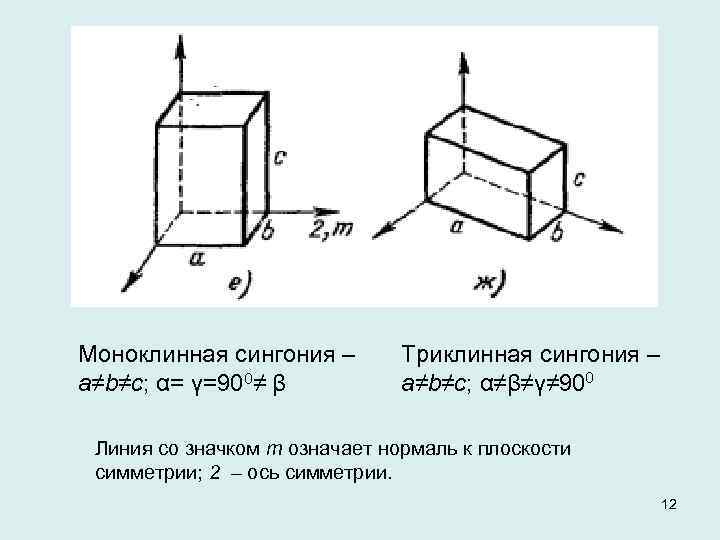Моноклинная сингония – a≠b≠c; α= γ=900≠ β Триклинная сингония – a≠b≠c; α≠β≠γ≠ 900 Линия со значком m означает нормаль к плоскости симметрии; 2 – ось симметрии. 12

Операции и элементы симметрии. Операции симметрии перемещают предмет в новую пространственную пози цию, которую не возможно отличить от первоначально занимаемой. Происходит отображение объекта, не вызывая его искажения. Операции симметрии могут повторяться бесконечное количество раз. Выделяют следующие операции симметрии: 1. Трансляция пере мещениематериального объекта в определенном направлении строго на установленную величину. Трансляционная симметрия является наиболее важным свойством симметрии кристалла. Для того чтобы обозначить симметрию в компактной форме, были введены специальные символы. 13

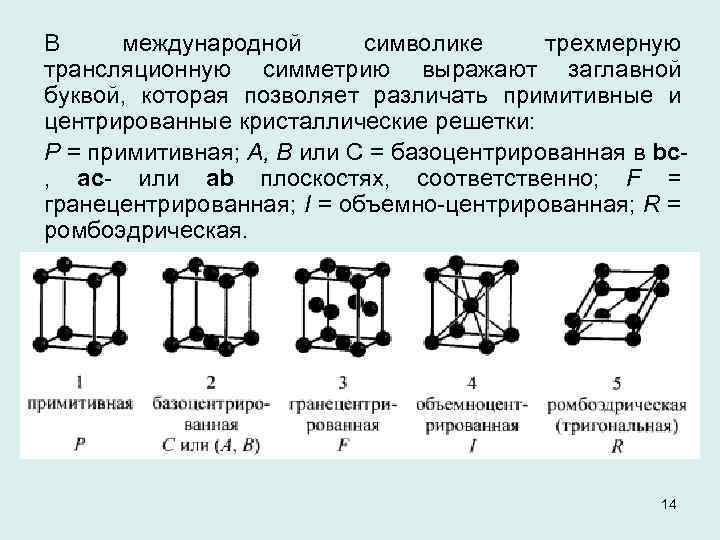В международной символике трехмерную трансляционную симметрию выражают заглавной буквой, которая позволяет различать примитивные и центрированные кристаллические решетки: Р = примитивная; А, В или С = базоцентрированная в bc , ас или аb плоскостях, соответственно; F = гранецентрированная; I = объемно центрированная; R = ромбоэдрическая. 14

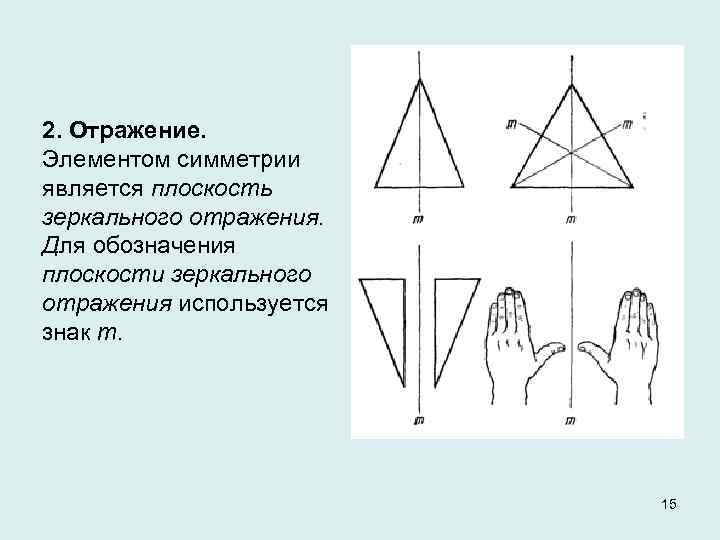2. Отражение. Элементом симметрии является плоскость зеркального отражения. Для обозначения плоскости зеркального отражения используется знак т. 15

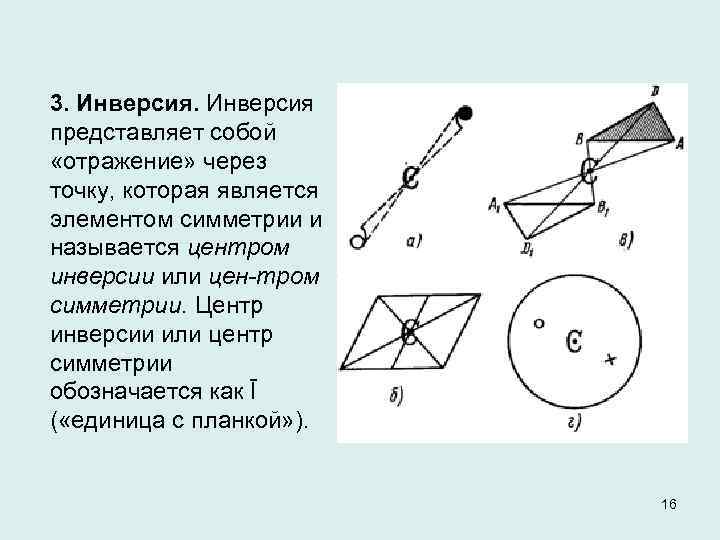3. Инверсия представляет собой «отражение» через точку, которая является элементом симметрии и называется центром инверсии или цен тром симметрии. Центр инверсии или центр симметрии обозначается как Ī ( «единица с планкой» ). 16

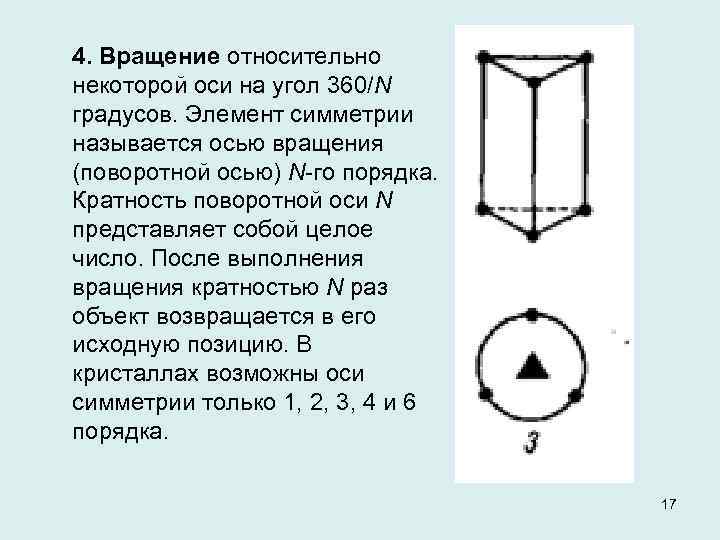4. Вращение относительно некоторой оси на угол 360/N градусов. Элемент симметрии называется осью вращения (поворотной осью) N го порядка. Кратность поворотной оси N представляет собой целое число. После выполнения вращения кратностью N раз объект возвращается в его исходную позицию. В кристаллах возможны оси симметрии только 1, 2, 3, 4 и 6 порядка. 17

5. Инверсионно-поворотная симметрия. Элемент симметрии называется ин версионно поворотной осью или, для краткости, инверсионной осью. Этот элемент симметрии представляет собой сдвоенную операцию симметрии, которая включа ет два действия: сначала вращение на угол 360/N градусов, а затем немедленное отражение в центре симметрии, расположенном на этой на оси. Зеркально-поворотные оси — представляют собой совместное действие по воротной оси N го порядка с последующим отражением в плоскости симметрии, перпендикулярной этой оси. 18

6. Винтовое вращение. Элементом симметрии является винтовая ось. Винто вое вращение имеет место, если существует трансляционная симметрия в направ лении оси. Результатом действия винтовой оси является вращение 360/N градусов с последующим смещением, параллельным этой оси. Винтовые оси обозначаются как NM. N выражает вращательный компонент, а дробь М/N— компонент смещения как доля вектора элементарной трансляции. 19

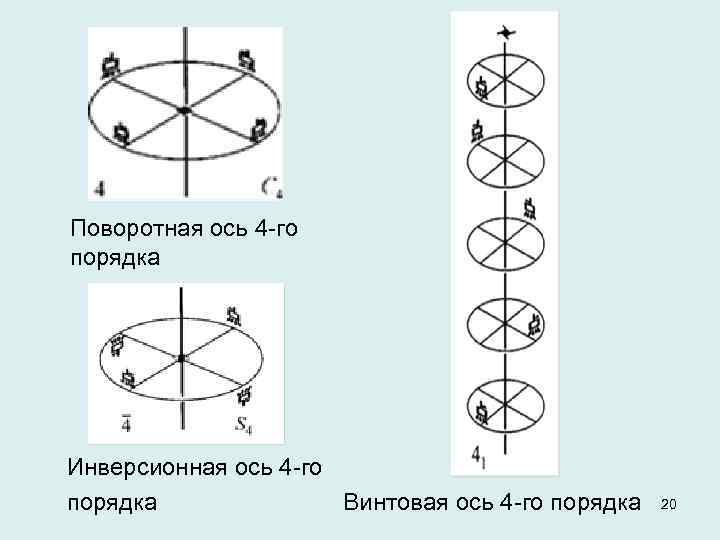Поворотная ось 4 го порядка Инверсионная ось 4 го порядка Винтовая ось 4 го порядка 20

7. Скользящее отражение. Плоскость скользящего отражения представляет собой совместное действие зеркальной плоскости сим метрии с последующим смещением в этой плоскости на определенную часть эле ментарной трансляции. Плоскости скользящего отражения обозначаются буквами — а, b, с, n, d или е, символ указывает направление скольжения относительно элементарной ячейки. Символы а, b и с показывают, что смещение происходит параллельно базисным векторам а, b и с. Плоскости скользящего отражения n и d включают смещения в диагональном направлении. Символ е указывает на скольжение в двух плоскостях симметрии, которые расположены взаимно перпендикулярно другу. 21

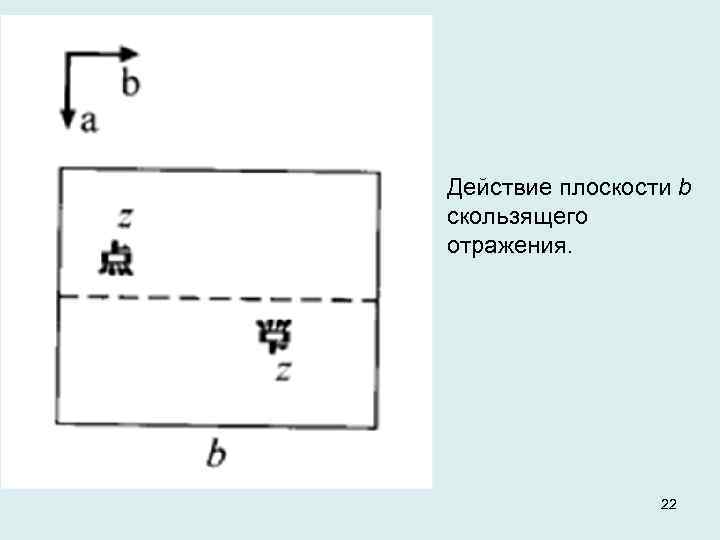Действие плоскости b скользящего отражения. 22

Точечные группы симметрии Геометрическое тело может иметь несколько элементов симметрии одновре менно, но их набор не может быть произвольным. Например, если имеется только одна плоскость симметрии, то поворотная ось не может проходить наклонно к этой плоскости. Ось должна лежать либо в плоскости симметрии, либо быть перпендику лярна к ней. Возможные комбинации элементов симметрии, исключая трансляци онную симметрию, называются точечными группами. Это означает, что любая дозволенная комбинация элементов симметрии имеет одну уникальную точку (или одну уникальную ось или плоскость) которая является общей для всех элементов симметрии. Операции симметрии можно рассматривать как элементы, которые создают точечную группу. 23

Кратность (порядок) точечной группы симметрии определяет мак симальное количество эквивалентных точек, которое можно получить из од ной точки, преобразуя ее всеми опе рациями симметрии, входящими в группу. Символ точечной группы состоит из перечня элементов симметрии, например m m 2 или 4 m m m. В них записываются все существующие плоскости симметрии, а поворотные оси симметрии, которые автома тически возникают в результате присутствия плоскостей симметрии, опускаются. 24

При записи символа точечной группы симметрии используют следующие правила: 1. Ориентация элементов симметрии соотносится с системой координат хуz. Ось симметрии более высокой крат ности ( «главная ось» ) выбирается как ось OZ. 2. Центр симметрии записывается только тогда, когда он является единственным элементом симметрии. Его символ Ī. 3. Элемент симметрии, встречающийся неоднократно, поскольку он размно жается другими элементами симметрии, записывается только однажды. 25

4. Плоскость симметрии, которая является перпендикулярной к оси симмет рии, обозначена наклонной чертой справа, например 2/т = плоскость. Одна ко плоскости симметрии перпендикулярные , поворотным осям вращения с нечетными кратностями обычно не обозначаются в форме 3/т, а изобража ются как инверсионно поворотные оси 6 го порядка. 5. Взаимная ориентация различных элементов симметрии выражена последо вательностью, в которой они перечислены. Ориентация элементов симмет рии соотносится с системойкоординат. Если поворотная ось симметрии самой высокой кратности представляет собой ось 2 го порядка, то последо вательность х у z, то есть элемент симметрии в направлении ОХ записывается первым. 26

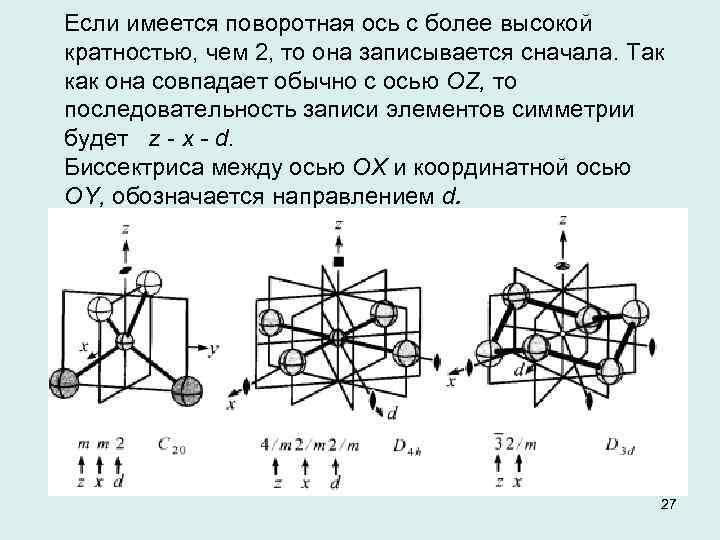Если имеется поворотная ось с более высокой кратностью, чем 2, то она записывается сначала. Так как она совпадает обычно с осью ОZ, то последовательность записи элементов симметрии будет z х d. Биссектриса между осью ОХ и координатной осью ОY, обозначается направлением d. 27

6. Точечные группы кубической сингонии имеют четыре поворотных оси 3 го порядка, которые пересекаются под углами 109, 47° (по четырем телесным диагоналям куба. В направлениях х, у, и z имеются поворотные оси 4 го порядка, инверсионно поворотные оси четвертого порядка или оси 2 го порядка, а также плоскости симметрии, перпендикулярные этим осям. В шести направлениях присутствуют также пово ротныеоси 2 го порядка и плоскости зеркального отражения. Цифра 3 во второй позиции символа (направление х + у + z) показывает, что данная точечная группа относится к кубической сингонии. 28

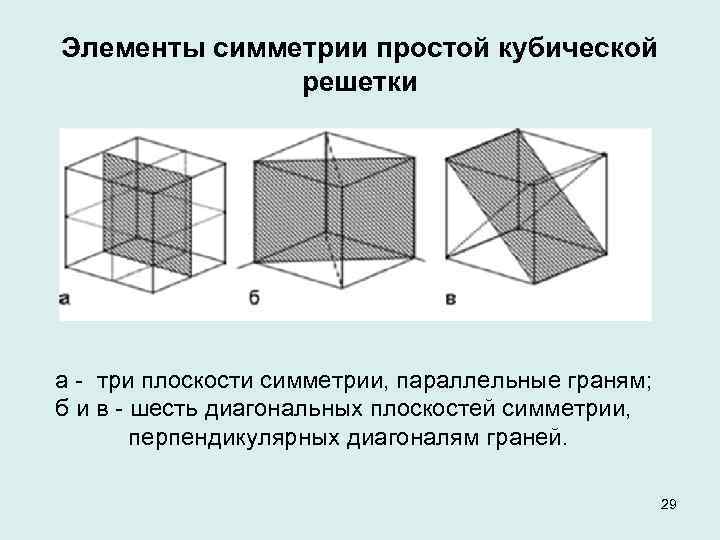Элементы симметрии простой кубической решетки а три плоскости симметрии, параллельные граням; б и в шесть диагональных плоскостей симметрии, перпендикулярных диагоналям граней. 29

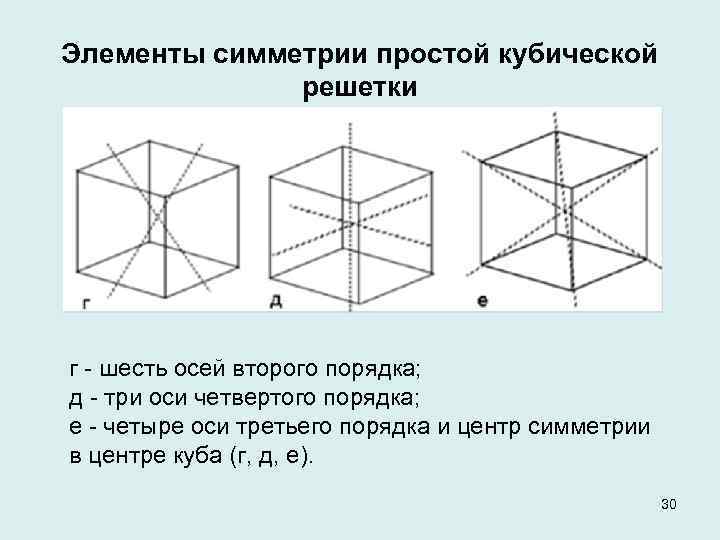Элементы симметрии простой кубической решетки г шесть осей второго порядка; д три оси четвертого порядка; е четыре оси третьего порядка и центр симметрии в центре куба (г, д, е). 30

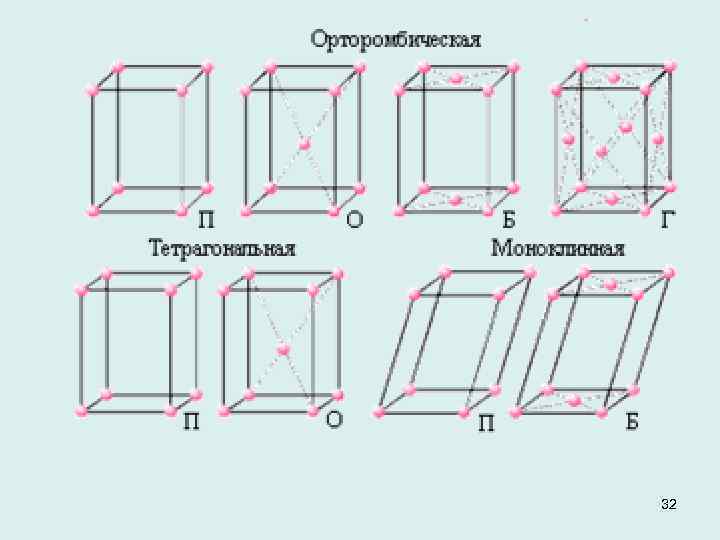
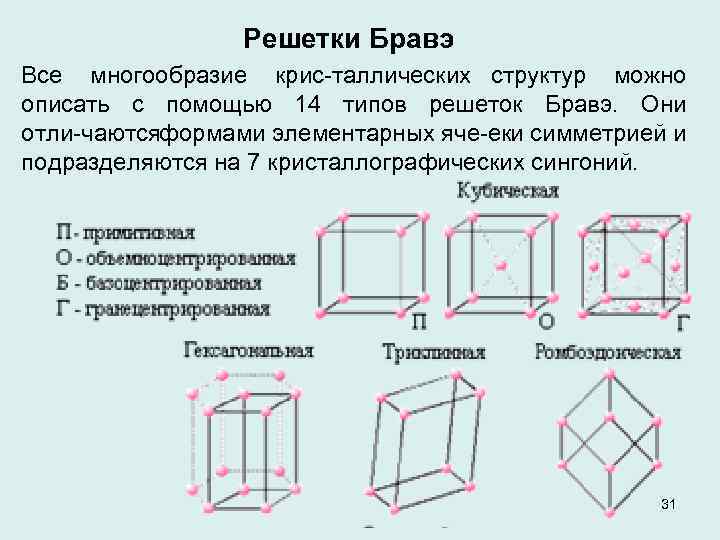Решетки Бравэ Все многообразие крис таллических структур можно описать с помощью 14 типов решеток Бравэ. Они отли чаютсяформами элементарных яче еки симметрией и подразделяются на 7 кристаллографических сингоний. 31

32

Пространственные группы симметрии Пространственной группой симмет рии называется совокупность всех возможных элементов симметрии кристаллической структуры, включая трансляционную. Каждой точечной группе соответ ствует несколько пространственных групп. Например, точечной группе m 3 m соответствуют пространственные группы F m 3 m (Na. Cl) и F d 3 m (алмаз), а также Р т. Зт (перовскит Са. Тi. Oз ) и другие. Из записи полного символа пространственных групп кристаллов Na. Cl и алмаза видно, что набор элементов симметрии у них разный: F m 3 m - F 4/m 3 2/m F d 3 m - F 4/d 3 2/m 33

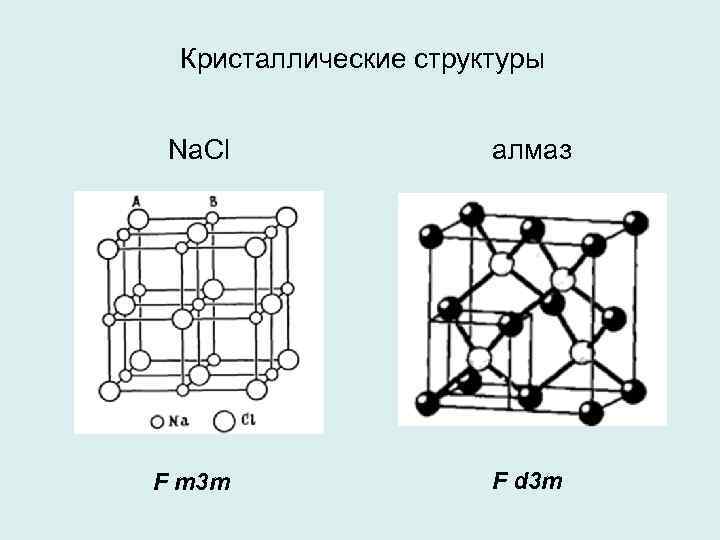Кристаллические структуры Na. Cl F m 3 m алмаз F d 3 m

Из пространственной группы симметрии кристалла можно получить ее точечную группу. Для этого надо мысленно уничтожить все трансляции: превратить плоскости скользящего отражения в зеркальные плоскости, винтовые оси в поворот ные оси симметрии, перенести все оставшиеся элементы симметрии так, чтобы они пересекались в одной точке. Так выводят 230 пространственных групп симметрии кристал лической структуры, илифедоровских групп симметрии, которые могут коррелировать с 32 точечными группами, которые называются кристаллическими классами (клас сами симметрии). 35

32 класса симметрии и соответствующие кристаллические системы (сингонии) 36

Правила записи символов пространственных групп Из за наличия в кристаллах трехмерной трансляционной симметрии операции симметрии могут взаимодей ствоватьтолько конечным числом способов. Каждая из существующих 230 возможностей их взаимодействия характеризует определенную пространственную группу: …………………. . . Символ для группы начинается с заглавной буквы Р, А, В, С, F, I или R, который выражает присутствие трансля ционной симметрии в трех измерениях и типа центровки элементарной ячейки. Перечисляются другие элементы симметрии согласно правилам, аналогичным для точечных групп. Базисные векторы а, b и с определяют систе му координат. 37

Если несколько видов элементов симметрии существуют в одном направлении (например, параллельно расположены поворотные оси 2 го порядка и винтовая ось 21), то в символе пространственной группы записывается только один. Обозначение зеркальных плоскостей симметрии является при оритетнымпо сравнению с плоскостями скользящего отражения, а поворотные оси доминируют над винтовыми осями. Распределение кристаллов по 230 пространственным группам крайне не равномерно. Практически большин ство изученных кристаллических структур описываются 3— 4 десятка ми пространственных групп. Осталь ные группы встречаются значительно реже, а для многих еще не найдены представители. 38

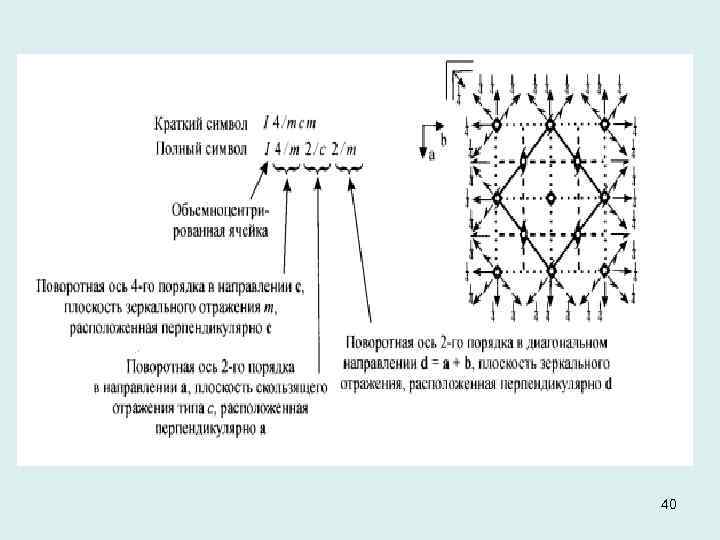
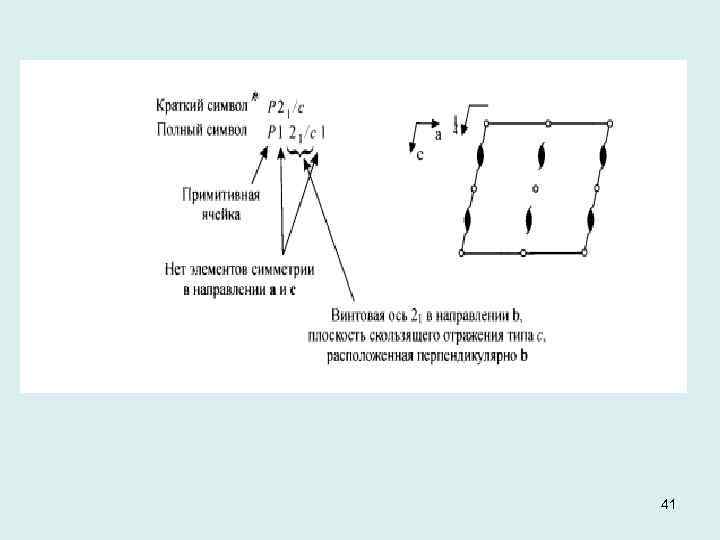
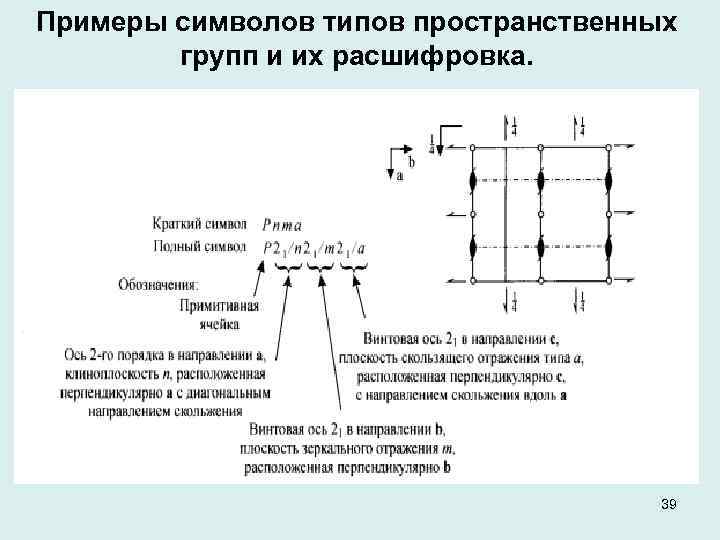Примеры символов типов пространственных групп и их расшифровка. 39

40

41