Элементы комбинаторики Комбинаторика раздел математики в котором

Элементы комбинаторики Комбинаторика – раздел математики, в котором изучаются вопросы о том, как определить сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Например: сколько различных четырехзначных чисел можно составить с помощью цифр 1, 2, 3, 4 без повторения цифр?

Основные правила комбинаторики 1. Правило сложения Если элемент A можно выбрать n способами, а элемент B можно выбрать m способами, то выбрать A или B можно n+m способами. Из пункта А в пункт Б можно добраться: – самолетом (2 авиамаршрута) – поездом (1 маршрут) – автобусом (3 маршрута) Общее число маршрутов 2+1+3=6

Основные правила комбинаторики 2. Правило умножения Если элемент A можно выбрать n способами и, при любом выборе A (то есть независимо), элемент B можно выбрать m способами, то пару (A, B) можно выбрать n*m способами. Если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.

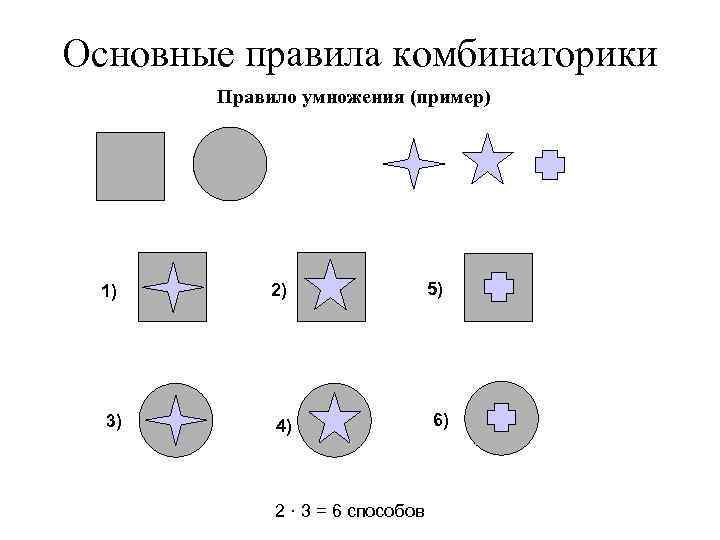
Основные правила комбинаторики Правило умножения (пример) 1) 3) 2) 4) 2 · 3 = 6 способов 5) 6)

Очень часто для наглядного решения задач применяются круги Эйлера. Пример 1. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним из данных языков?

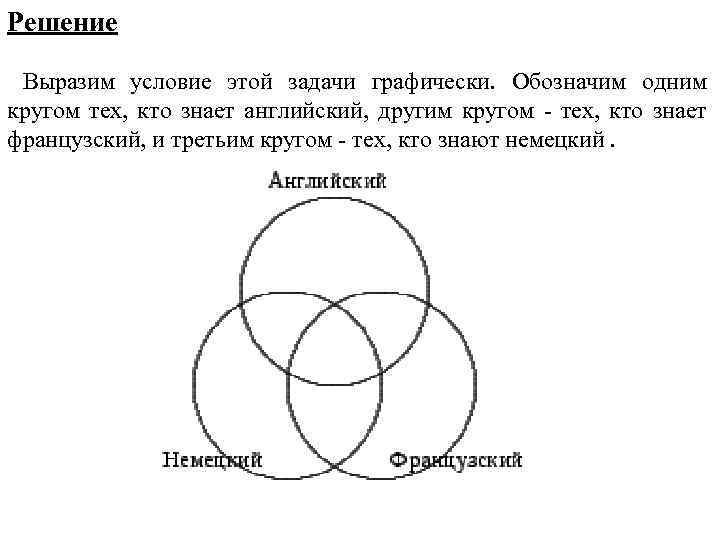
Решение Выразим условие этой задачи графически. Обозначим одним кругом тех, кто знает английский, другим кругом - тех, кто знает французский, и третьим кругом - тех, кто знают немецкий.

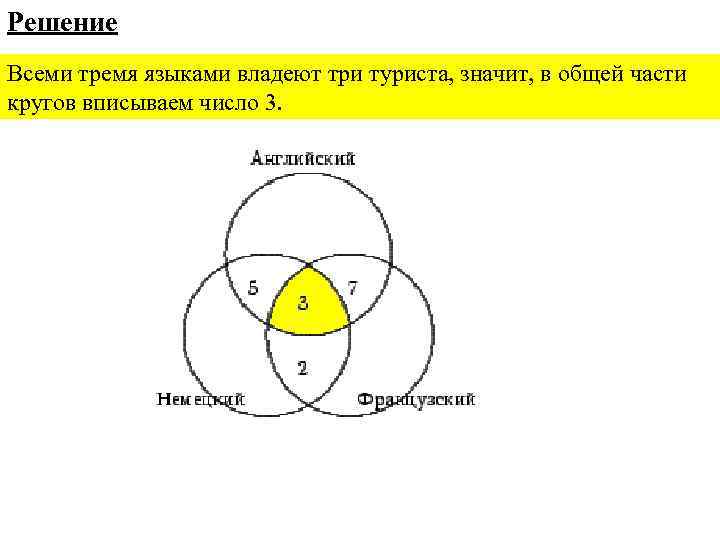
Решение Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3.

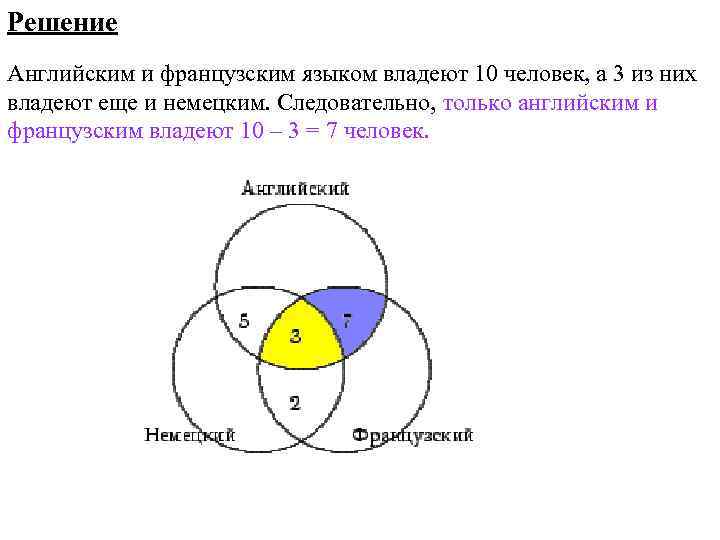
Решение Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10 – 3 = 7 человек.

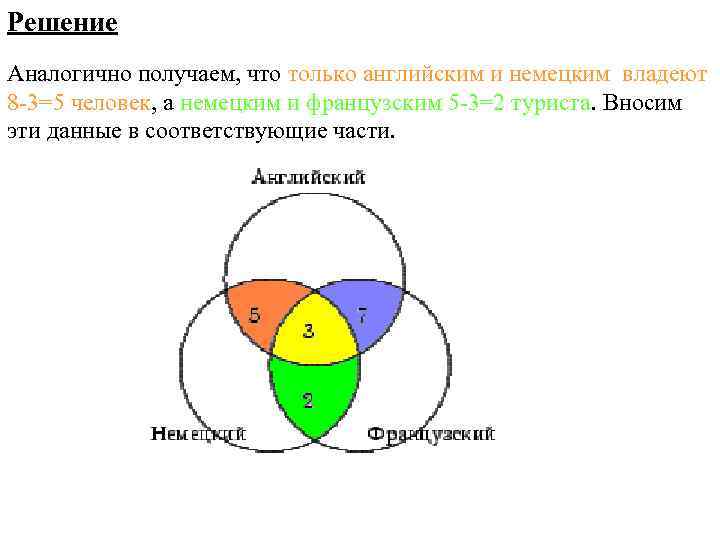
Решение Аналогично получаем, что только английским и немецким владеют 8 -3=5 человек, а немецким и французским 5 -3=2 туриста. Вносим эти данные в соответствующие части.

Решение Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским - 30 человек. Вносим эти данные в соответствующие части. И так, 20+13+30+5+7+2+3 = 80 туристов знают хотя бы один язык Следовательно, 100 – 80 = 20 человек не владеют ни одним из данных языков.

Элементы комбинаторики 1. Размещения Пусть дано множество, состоящее из n элементов. Размещением из n элементов по k элементов называется упорядоченное подмножество, содержащее k различных элементов данного множества. Эти подмножества могут отличаться друг от друга составом элементов или порядком их следования.

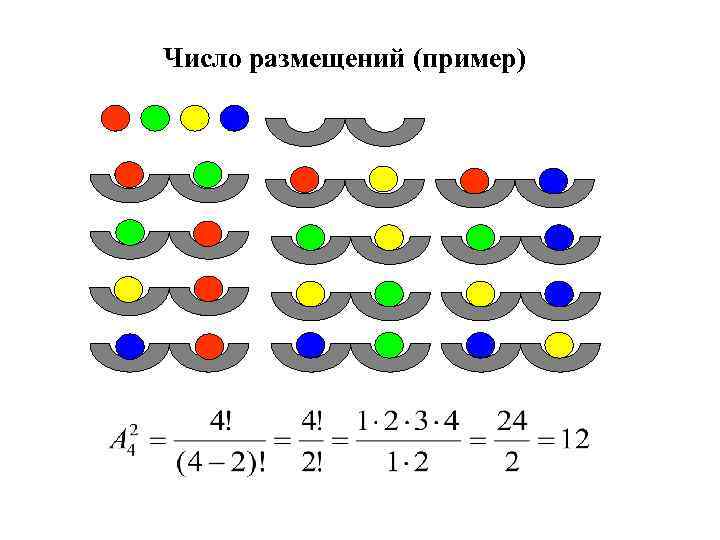
Число размещений (пример)

Элементы комбинаторики 2. Перестановки Пусть дано множество, состоящее из n элементов. Перестановкой из n элементов называется размещение из n элементов по n элементов. Различные перестановки отличаются друг от друга только порядком следования элементов.

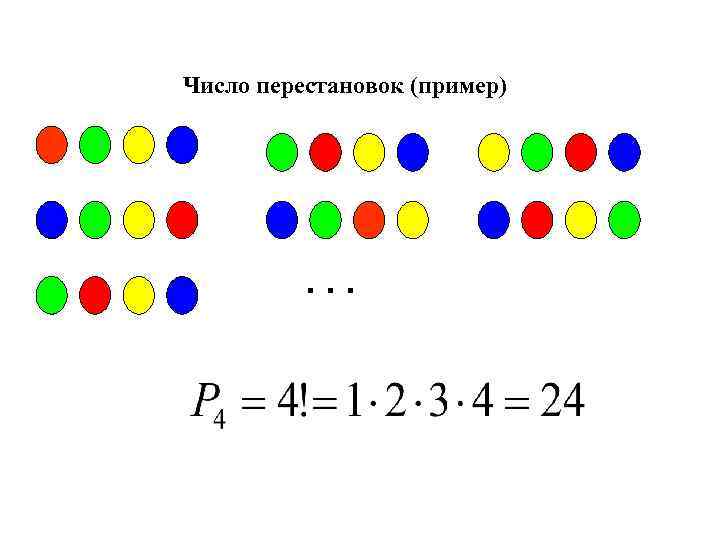
Число перестановок (пример) . . .

Число перестановок (пример) « Проказница Мартышка, Осел, Козел, Да косолапый Мишка Затеяли играть квартет …Стой, братцы стой! – Кричит Мартышка, - погодите! Как музыке идти? Ведь вы не так сидите… И так, и э так пересаживались – а музыка на лад не идет. Тут пуще прежнего пошли у них раздоры. И споры, Кому и как сидеть…» Вероятно, крыловские музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Сколько?

Элементы комбинаторики 3. Сочетания Пусть дано множество, состоящее из n элементов. Сочетанием из n элементов по k элементов называется любое подмножество, которое содержит k различных элементов данного множества. Различные сочетания отличаются друг от друга только составом элементов.

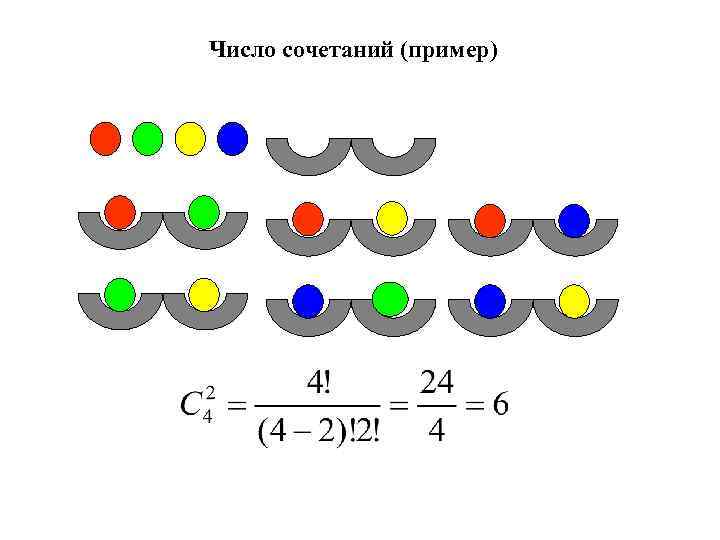
Число сочетаний (пример)

Число сочетаний (пример) У одного человека 7 книг по математике, а у второго – 9. Сколькими способами они могут обменять друг у друга две книги на две книги. Решение Так как порядок следования книг не имеет значения, то выбор 2 х книг - сочетание. Первый человек может выбрать 2 книги способами. Второй человек может выбрать 2 книги способами. Всего по правилу произведения возможно 21*36=756 вариантов. .

Задача на комбинированную выборку В колоде – 36 карт: четыре масти по девять карт (от шестёрки до туза). Сколько существует способов составить набор из шести карт так, чтобы в него вошли два короля, три десятки и одна дама? В данной задаче важно определить, на какие классы надо разбить всю совокупность, чтобы выбор осуществлялся из каждого класса в определенном количестве. Схема решений: – королей всего четыре, из них берем два, способов – десяток всего четыре, из них берем три, способов – дам всего четыре, из них берем одну, способов Поскольку требуется сделать одновременный выбор то, по правилу умножения, число комбинированных наборов равно 6 ∙ 4 = 96. ; ; .

Задание (для самостоятельной работы) Задача 1. Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы? Задача 2. Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет из спортлото или автомотолотереи? Задача 3. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать? Задача 4. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр. Задача 5. При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?