Элементы физики звёзд 1 Элементы физики звёзд

Элементы физики звёзд 1

Элементы физики звёзд (4 h). 1. 2. 3. 4. 5. 6. 7. Многообразие в мире звёзд. Диаграмма спектр-светимость (Герцшпрунга-Рессела). Спектральные классы звезд. Внутреннее строение звёзд. Политропные и другие модели звезд. Гиганты, сверхгиганты, субкарлики, белые карлики. Переменные звезды. Пульсирующие переменные звезды. Сверхновые звезды. Пульсары. Нейтронные звёзды. Черные дыры. Гравитационный радиус тела. Эффект замедления времени. Сфера Шварцшильда. 2

Многообразие в мире звёзд. Диаграмма спектр-светимость (Hertzsprung–Russell). Спектральные классы звезд. 3

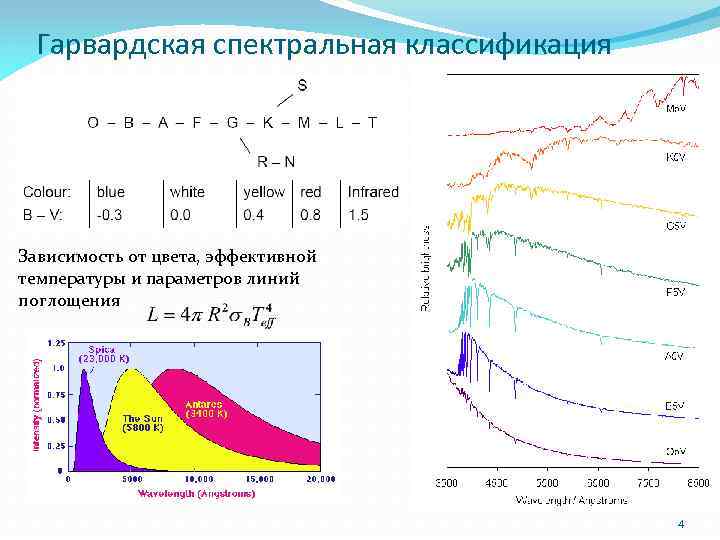Гарвардская спектральная классификация Зависимость от цвета, эффективной температуры и параметров линий поглощения 4

Спектральная классификация звезд (отражена также зависимость цвета звезды от ее светимости) 5

Полоса λ [мкм] Sν [Вт м− 2 Гц− 1] U 0. 36 3. 98 × 10 − 11 B 0. 44 6. 95 × 10 − 11 V 0. 55 3. 63 × 10 − 11 R 0. 70 1. 70 × 10 − 11 I 0. 90 8. 29 × 10 − 12 J 1. 25 3. 03 × 10 − 12 K 2. 22 3. 84 × 10 − 13 L 3. 60 6. 34 × 10 − 14 M 5. 00 1. 87 × 10 − 14 N 10. 60 1. 03 × 10 − 15 Потоки от звезды класса A 0 V и mv = 0 Полосы пропускания фильтров, в которых измеряется поток излучения от звезд. Черной линией показан спектр излучения звезды класса G 5 V (спектр близок к солнечному) при наблюдении в конечной полосе частот (Tx – передаточная функция фильтра) Johnson UBVRIJHKLMN U = near UV, B = blue, V = visual(green), R = Kron-Cousins RCIC red, I = near infrared, JHKLMN = infrared Ströemgren uvby. Hβ Gunn ugriz Δm ~ Δfx/fx ~ 0. 01 (узкая полоса = точность) 6 Sloan Digitial Sky Survey filters: u‘ g‘ r‘ i‘ z‘

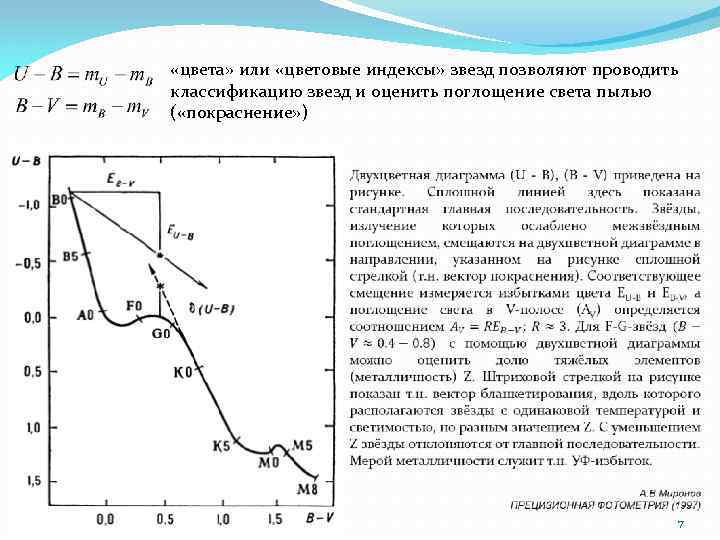«цвета» или «цветовые индексы» звезд позволяют проводить классификацию звезд и оценить поглощение света пылью ( «покраснение» ) 7

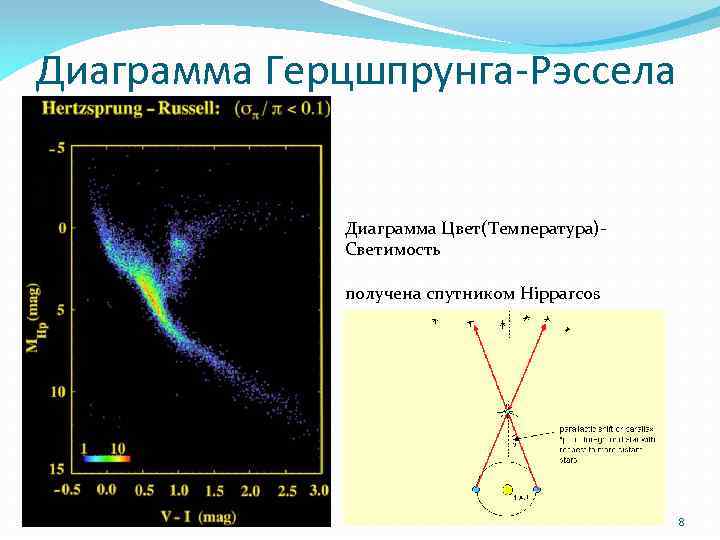Диаграмма Герцшпрунга-Рэссела Диаграмма Цвет(Температура)Светимость получена спутником Hipparcos 8

Гиганты, сверхгиганты, субкарлики, белые карлики 9

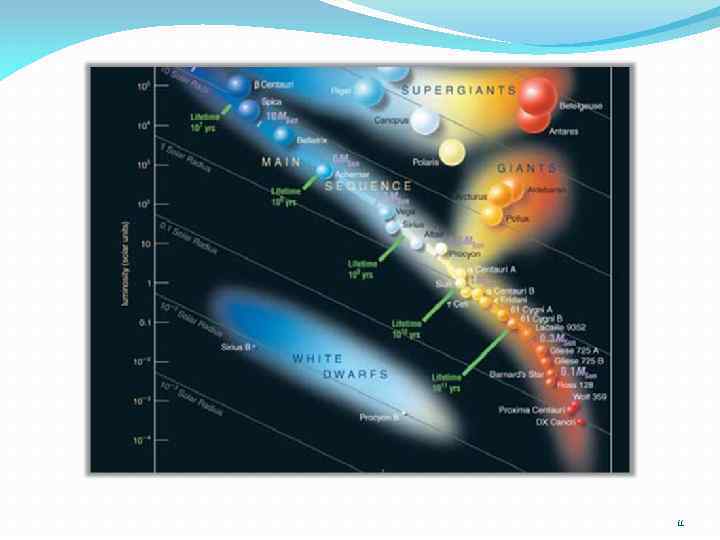
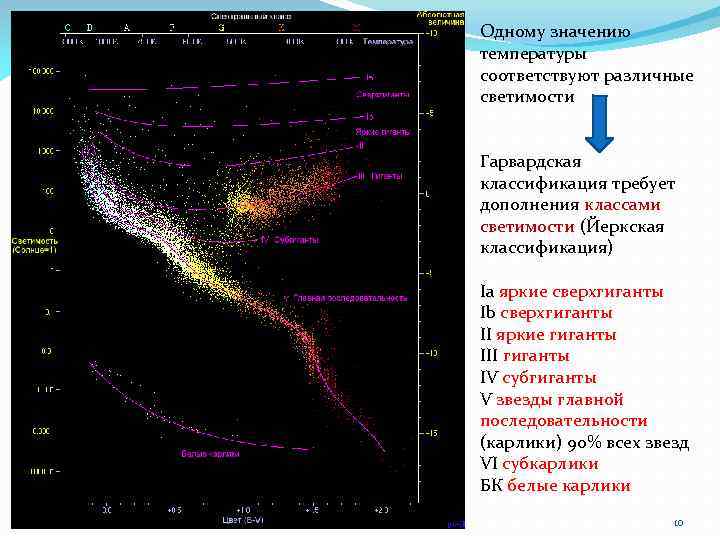Одному значению температуры соответствуют различные светимости Гарвардская классификация требует дополнения классами светимости (Йеркская классификация) Ia яркие сверхгиганты Ib сверхгиганты II яркие гиганты III гиганты IV субгиганты V звезды главной последовательности (карлики) 90% всех звезд VI субкарлики БК белые карлики 10

11

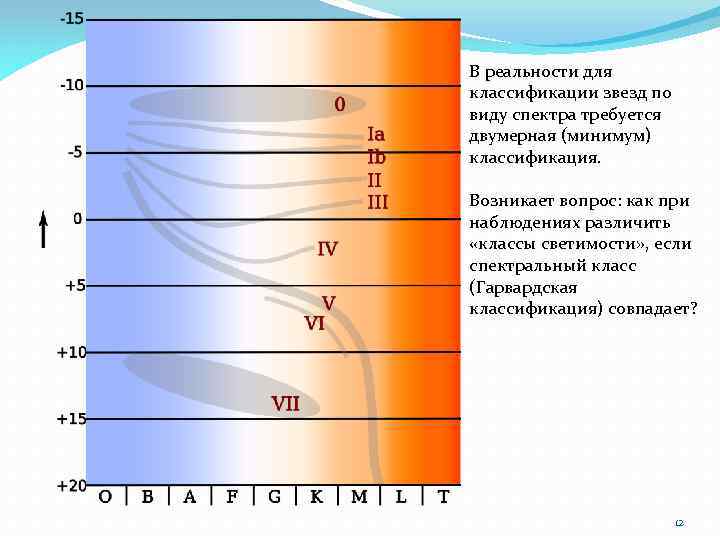В реальности для классификации звезд по виду спектра требуется двумерная (минимум) классификация. Возникает вопрос: как при наблюдениях различить «классы светимости» , если спектральный класс (Гарвардская классификация) совпадает? 12

• I. Сверхгиганты. o Ia-0 гипергиганты или очень яркие сверхгиганты. o Ia яркие сверхгиганты, такие как Денеб (спектр A 2 Ia). o Iab сверхгиганты средней яркости. o Ib менее яркие сверхгиганты, например, Бетельгейзе (спектр M 2 Ib). • II. Яркие гиганты. o IIa, например: в Scuti (HD 173764) (спектр G 4 IIa). o IIab, например: HR 8752 (спектр GOIab). o IIb, например: HR 6902 (спектр G 9 IIb). • III. Нормальные гиганты. o IIIa, например: р Persei (спектр M 4 IIIa). o IIIab, например: 6 Reticuli (спектр M 2 IIIab). o IIIb, например: Поллукс (спектр K 2 IIIb). • IV. Субгиганты. o IVa, например: £ Reticuli (спектр K 1 -2 IVa-III). o IVb, например: HR 672 A (спектр G 0. 5 IVb). • V. Главная последовательность (карлики). o Va, например: AD Leonis (спектр M 4 Vae). o Vb, например: 85 Pegasi A (спектр G 5 Vb). • VI. Субкарлики (редко). • VII. Белый карлик (редко).

Внутреннее строение звёзд. Политропные и другие модели звезд 14

Звезда – сферически симметричная газовая конфигурация Теорема Рассэла-Фойгта: для звезды заданного химического состава и массы существует только одна равновесная конфигурация, удовлетворяющая граничным условиям (в общем случае не доказана) 15

Стационарные звезды. Гидростатическое равновесие 16

17

Теорема вириала 18

19

Тепловая устойчивость звезд. Отрицательная теплоемкость 20

21

Источники энергии звезд 22

Гравитационная и химическая энергия звезды Теорема вириала для самогравитирующего газового шара E∞=0 время Кельвина-Гельмгольца 23

Термоядерные источники энергии звезд Артур Эддингтон (1920): If, indeed, the sub-atomic energy in the stars is being freely used to maintain their great furnaces, it seems to bring a little nearer to fulfillment our dream of controlling this latent power for the well-being of the human race - or for its suicide. запас ядерной энергии Солнца В реальности лишь около 10 % массы Солнца может участвовать в термоядерных реакциях 24

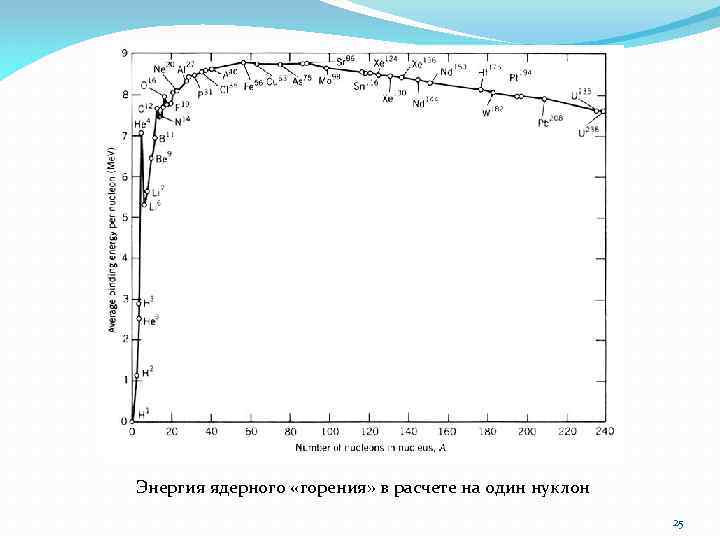Энергия ядерного «горения» в расчете на один нуклон 25

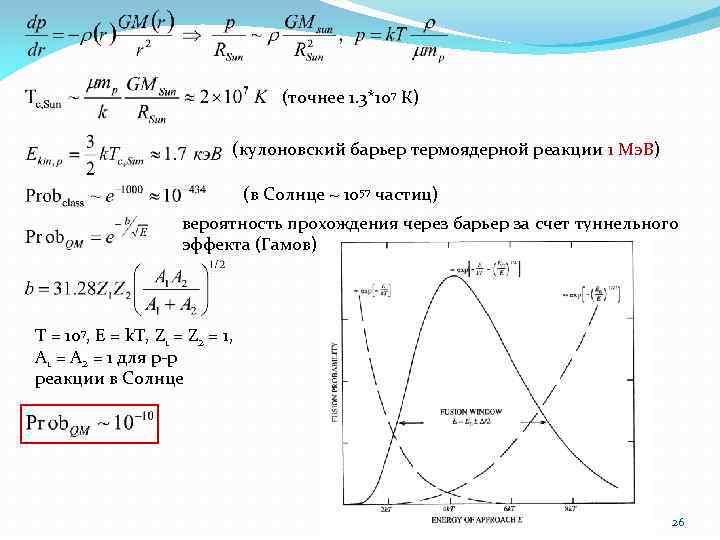(точнее 1. 3*107 К) (кулоновский барьер термоядерной реакции 1 Мэ. В) (в Солнце ~ 1057 частиц) вероятность прохождения через барьер за счет туннельного эффекта (Гамов) T = 107, E = k. T, Z 1 = Z 2 = 1, A 1 = A 2 = 1 для p-p реакции в Солнце 26

«Горение» водорода 27

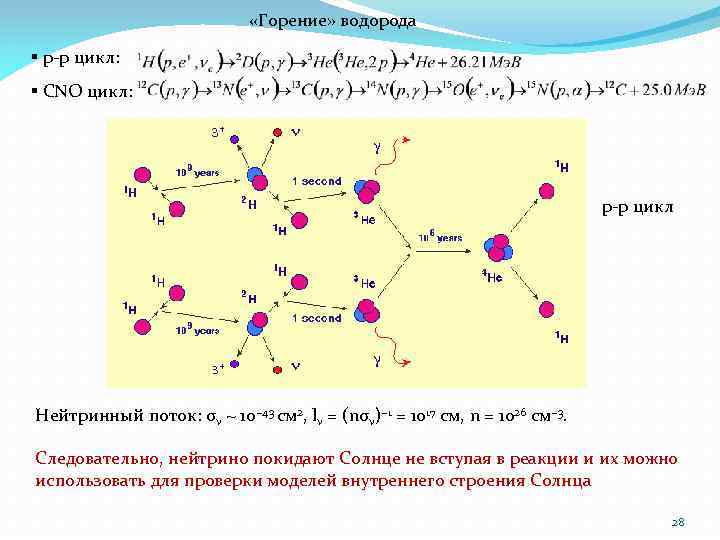«Горение» водорода § p-p цикл: § CNO цикл: p-p цикл Нейтринный поток: σν ~ 10− 43 см 2, lν = (nσν)− 1 = 1017 см, n = 1026 см− 3. Следовательно, нейтрино покидают Солнце не вступая в реакции и их можно использовать для проверки моделей внутреннего строения Солнца 28

29

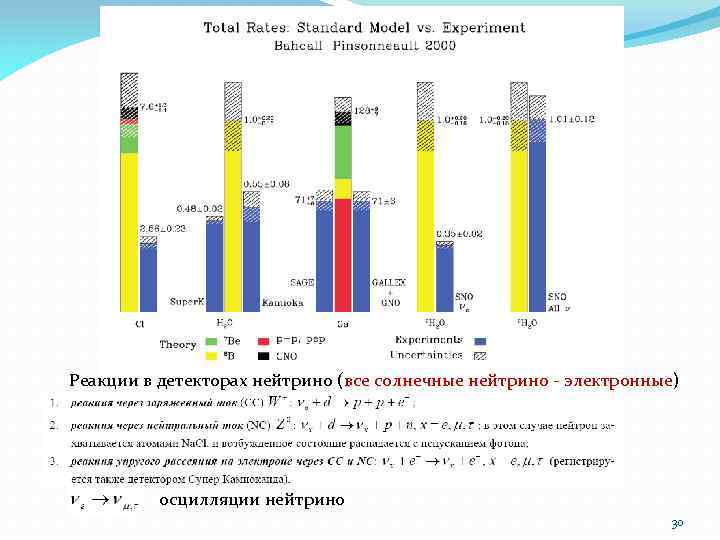Реакции в детекторах нейтрино (все солнечные нейтрино - электронные) осцилляции нейтрино 30

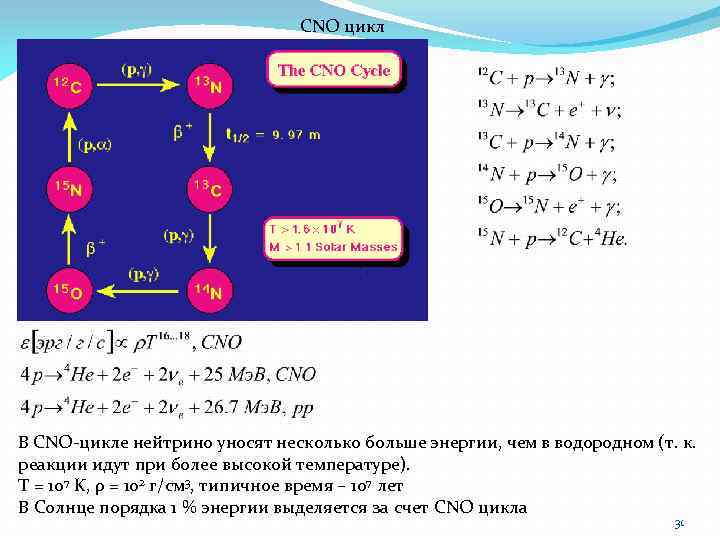CNO цикл , . В CNO-цикле нейтрино уносят несколько больше энергии, чем в водородном (т. к. реакции идут при более высокой температуре). T = 107 K, ρ = 102 г/см 3, типичное время – 107 лет В Солнце порядка 1 % энергии выделяется за счет CNO цикла 31

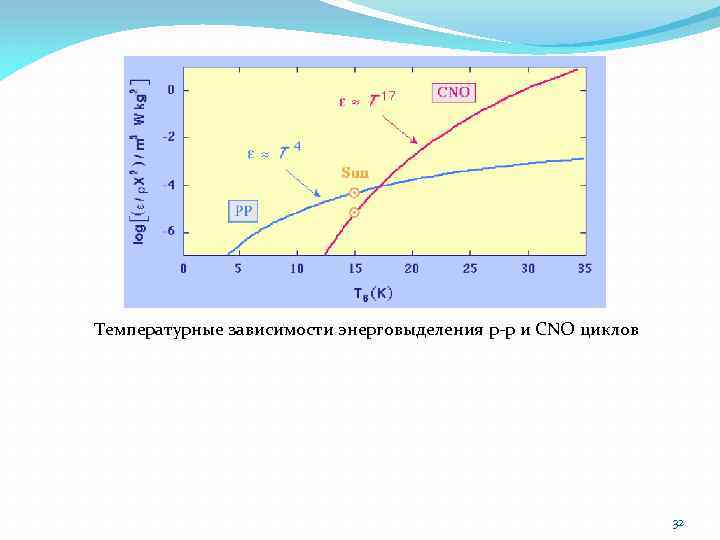Температурные зависимости энерговыделения p-p и CNO циклов 32

Горение элементов тяжелее водорода 33

T > 108 K реакция-поставщик медленных нейтронов для образования более тяжелых элементов в s-процессах T > 6*108 K 34

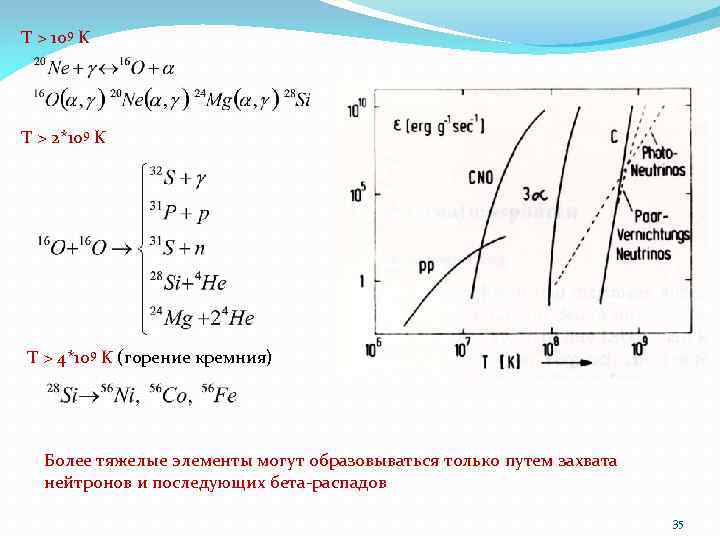T > 109 K T > 2*109 K T > 4*109 K (горение кремния) Более тяжелые элементы могут образовываться только путем захвата нейтронов и последующих бета-распадов 35

Перенос энергии в теле звезды 36

Большой Поток энергии Малый Сильный Быстрое Температурный градиент Охлаждение Слабый Медленное Радиативный Перенос энергии Конвективный Радиативный механизм переноса В непрозрачном веществе основной механизм переноса – рассеяние условие на среднюю длину свободного пробега (κ = κ(ρ, T) – τ = κlγ = 1 коэффициент поглощения) Непрозрачность: свободно-свободные и свободно-связанные переходы в атомах и рассеяние на свободных электронах диффузионное приближение 37

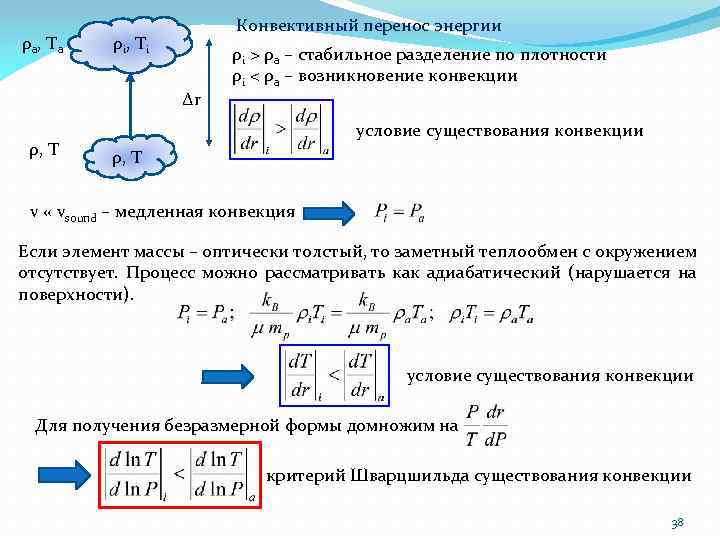ρa, Ta Конвективный перенос энергии ρi, Ti Δr ρ, T ρi > ρa – стабильное разделение по плотности ρi < ρa – возникновение конвекции условие существования конвекции ρ, T v « vsound – медленная конвекция Если элемент массы – оптически толстый, то заметный теплообмен с окружением отсутствует. Процесс можно рассматривать как адиабатический (нарушается на поверхности). условие существования конвекции Для получения безразмерной формы домножим на критерий Шварцшильда существования конвекции 38

Для адиабатического процесса: для одноатомного газа γ = 5/3 Если перенос лучистой энергии приводит к конвекция остановка конвекции высокая теплоемкость стимулирует возникновение конвекции 39

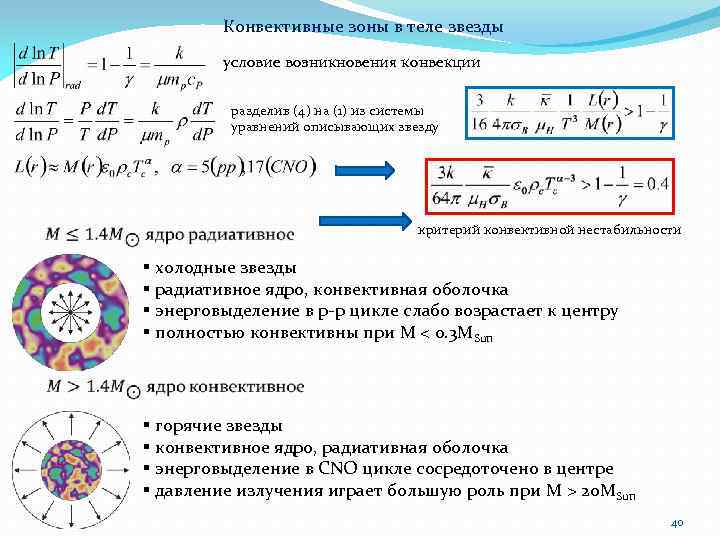Конвективные зоны в теле звезды условие возникновения конвекции разделив (4) на (1) из системы уравнений описывающих звезду критерий конвективной нестабильности § холодные звезды § радиативное ядро, конвективная оболочка § энерговыделение в p-p цикле слабо возрастает к центру § полностью конвективны при M < 0. 3 MSun § горячие звезды § конвективное ядро, радиативная оболочка § энерговыделение в CNO цикле сосредоточено в центре § давление излучения играет большую роль при M > 20 MSun 40

Полная система уравнений структуры звезды 41

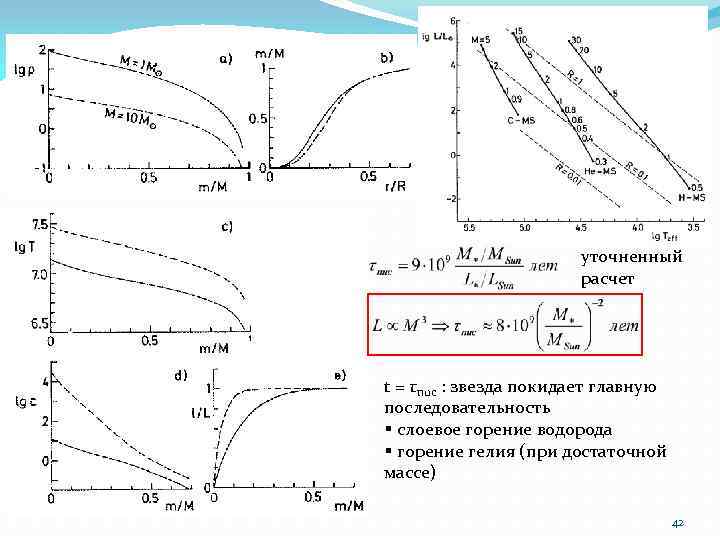уточненный расчет t = τnuc : звезда покидает главную последовательность § слоевое горение водорода § горение гелия (при достаточной массе) 42

43