Элементы алгебры Соответствия между множествами 4 час

Элементы алгебры Соответствия между множествами (4 час. )

• Алгебра – учение о решении уравнений • На современном этапе алгебра изучает операции и отношения на различных множествах.

Основные понятия алгебры • • Числовое выражение Выражение с переменной Числовое равенство Числовое неравенство Алгебраическая операция Уравнение Неравенство

Понятие соответствия Определение: Соответствием между множествами X и. Y называется всякое подмножество декартова произведения этих множеств.

Соответствия принято обозначать P, R, S, T Если S- соответствие между множествами X и Y, то

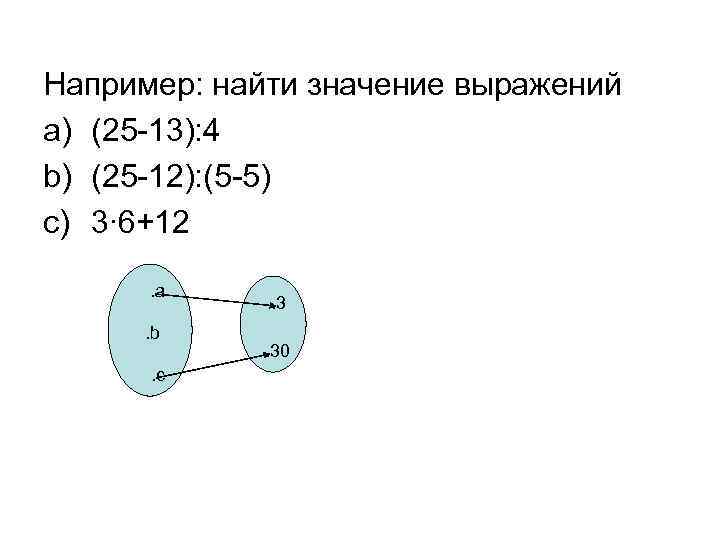
Например: найти значение выражений a) (25 -13): 4 b) (25 -12): (5 -5) c) 3∙ 6+12. a. b. c . 3. 30

Способы задания соответствий • Перечислением пар; • Указанием характеристического свойства соответствия; • С помощью графа.

• Например: R={(1; 3); (1; 5); (2; 3); (2; 5); (4; 5)} Соответствие R задано перечислением пар. Это же соответствие можно задать, указав характеристическое свойство соответствия. Пусть X={1, 2, 4, 6} и Y={3; 5} задано соответствие R- «a<b» , при условии, что и

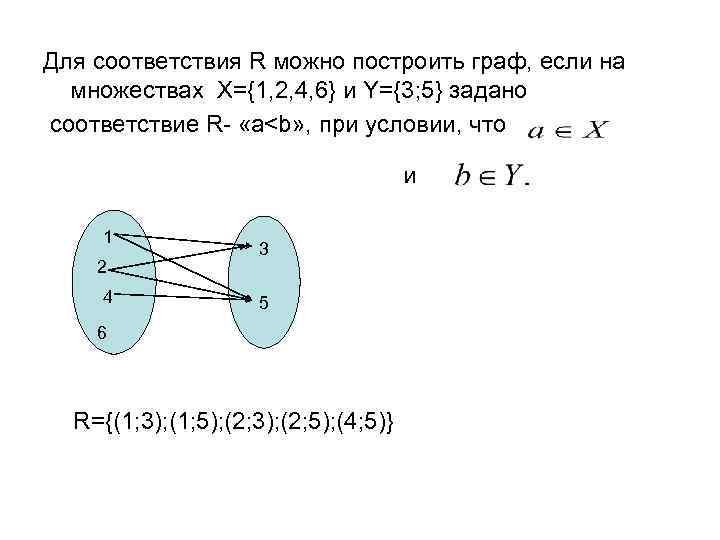
Для соответствия R можно построить граф, если на множествах X={1, 2, 4, 6} и Y={3; 5} задано соответствие R- «a<b» , при условии, что и 1 2 4 3 5 6 R={(1; 3); (1; 5); (2; 3); (2; 5); (4; 5)}

Иллюстрация соответствия • С помощью графа. • На координатной плоскости (с помощью графика).

Соответствие, обратное данному Определение: Пусть S- соответствие между множествами X и Y. Соответствие Между множествами Y и X называется обратным данному, если тогда и только тогда, когда

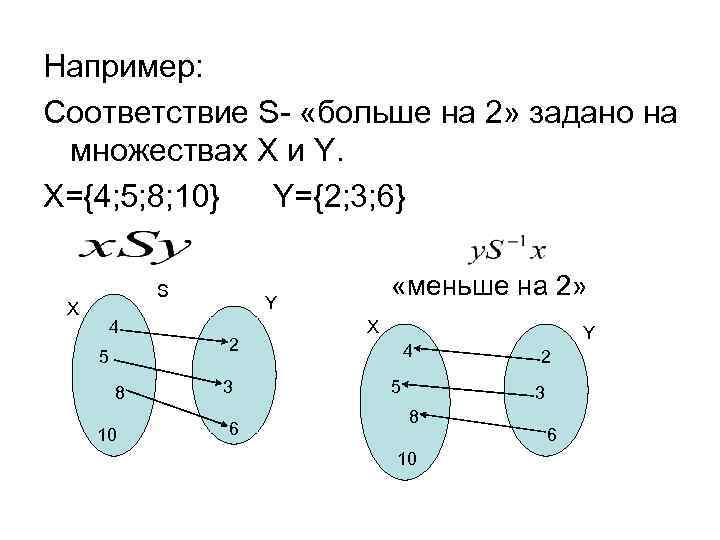
Например: Соответствие S- «больше на 2» задано на множествах X и Y. X={4; 5; 8; 10} Y={2; 3; 6} S X 4 5 8 10 «меньше на 2» Y 2 3 6 X 4 5 Y 2 3 8 10 6

Графики взаимно обратных соответствий симметричны относительно биссектрисы 1 -го и 3 -го координатных углов.

Взаимно однозначные соответствия • Определение: Взаимно однозначным соответствием между множествами X и Y называется такое соответствие, при котором каждому элементу множества X соответствует единственный элемент множества Y и каждый элемент множества Y соответствует только одному элементу множества X.

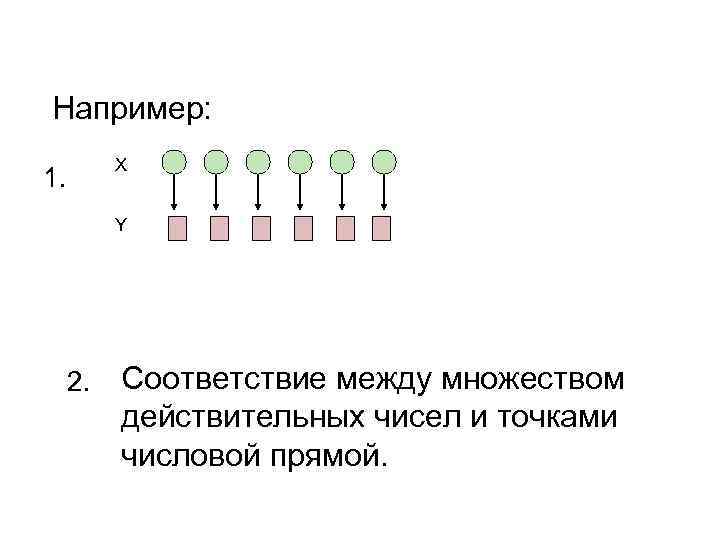
Например: X 1. Y 2. Соответствие между множеством действительных чисел и точками числовой прямой.

Равномощные множества Множества X и Y называются равномощными, если между их элементами можно установить взаимно однозначное соответствие.

Равномощные конечные множества называют равночисленными. Равночисленность в математике обозначается словами «столько же» .

Числовые функции • Определение: Числовой функцией называется такое соответствие между числовым множеством X и множеством R (действительных чисел), при котором каждому числу из множества X соответствует единственное число из множества R.

Множество X называют областью определения функции. Функции обозначают y = f(x), где x- аргумент, а y- значение функции. Множество чисел вида f(x) для всех x из области определения (множества X) называется областью значений функции.

• Задать функцию значит: • 1. Указать область определения функции • 2. указать правило (закон), по которому каждому числу из множества X соответствует единственное действительное число.

Способы задания функции • 1. Формула. • Например: у=2 х+5; y=sin 3 x y= Ln 6 x • 2. График. • С помощью одной и той же формулы можно задать различные функции, которые будут отличаться друг от друга областью определения.

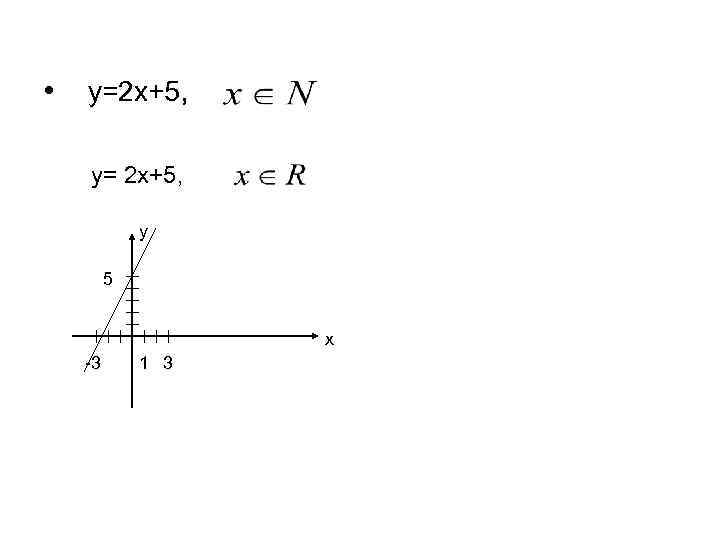
• y=2 x+5, y= 2 x+5, y 5 x -3 1 3

Свойства числовых функций 1. Функция f называется монотонной на некотором промежутке A, если на этом промежутке она возрастает или убывает.

Функция f называется возрастающей на некотором промежутке A, если для и из множества A любых чисел выполняется условие:

• Определение: • Функция y= f(x) называется возрастающей на некотором промежутке А, если для любых чисел и < из множества А выполняется условие: < y x

Функция f называется убывающей на некотором промежутке A, если для и из множества A любых чисел выполняется условие:

• Определение: • Функция y=f(x) называется убывающей на некотором промежутке А, если для любых чисел и выполняется условие: < > y x

Прямая пропорциональность. Определение: Прямой пропорциональностью называется функция вида y=kx, где k≠ 0 действительное число. K- коэффициент пропорциональности.

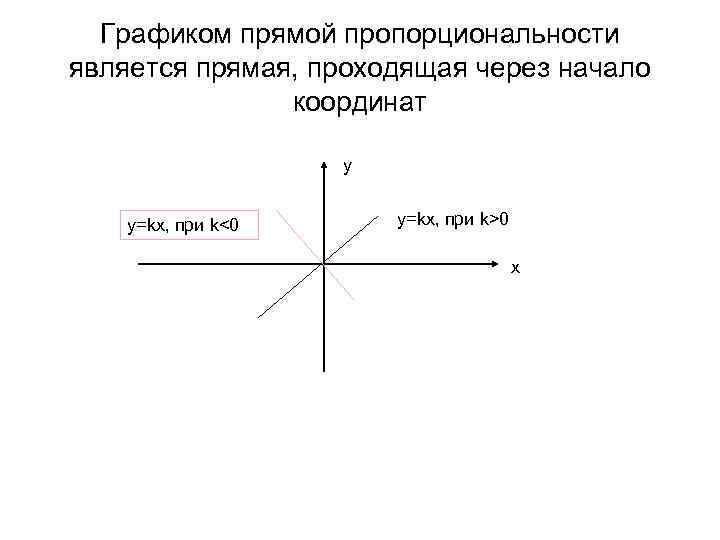
Графиком прямой пропорциональности является прямая, проходящая через начало координат y y=kx, при k<0 y=kx, при k>0 x

Свойства прямой пропорциональности • Областью определения функции y=kx и областью значений функции является множество действительных чисел. • Графиком прямой пропорциональности является прямая, проходящая через начало координат.

• При k>0 функция y=kx возрастает на всей области определения; при k<0 – убывает на всей области определения. • Если функция f- прямая пропорциональность и пары соответственных значений x и y, при чем то

Обратная пропорциональность • Определение: Обратной пропорциональностью называется функция, которая может быть задана при помощи формулы где k – неравное нулю число.

Свойства обратной пропорциональности • 1. Область определения и множество значений является множество действительных чисел, отличных от нуля. • 2. Графиком обратной пропорциональности является гипербола.

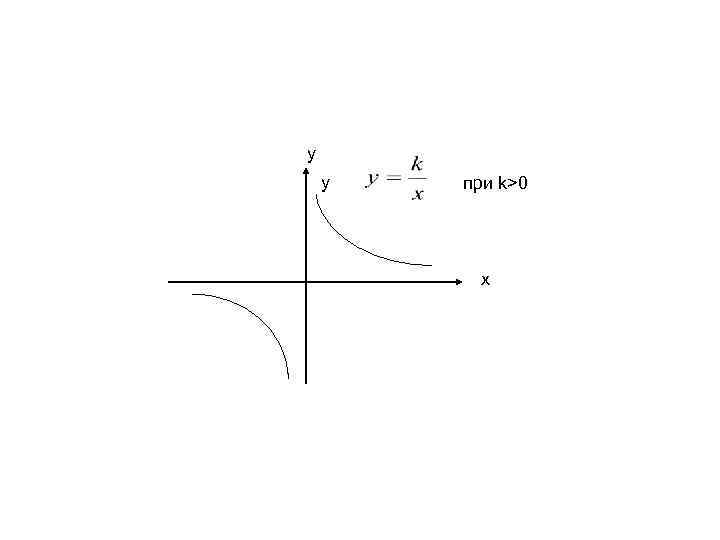
y y при k>0 x

• 3. При k>0 ветви гиперболы расположены в 1 -ой и 3 -ей четвертях. И функция является убывающей на всех промежутках области определения

• При k<0 ветви гиперболы расположены во 2 -ой и в 4 – ой четверти. • Функция является возрастающей на каждом промежутке области определения.

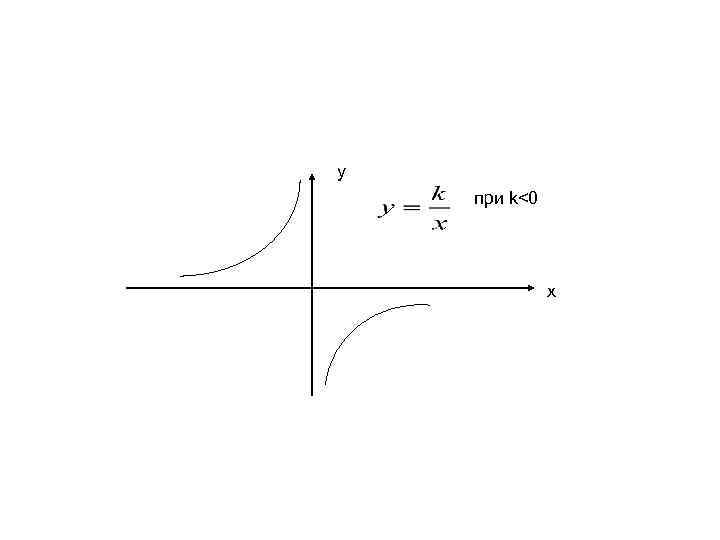
у при k<0 x

• 4. Если функция f- обратная пропорциональность и пары соответственных значений x и y, то С увеличением (уменьшением) значений переменной x в несколько раз соответствующее значение переменной y уменьшается (увеличивается) во столько же раз.

• Прямая и обратная пропорциональность являются математическими моделями многих реальных ситуаций.

Задача За 8 час. токарь изготовил 16 деталей. Сколько часов потребуется токарю на изготовление 48 деталей, если он будет работать с той же производительностью?

Решение • I способ (по определению прямой пропорциональности): • 16: 8=2(дет. в час)- производительность работы. • 48: 2=24(час)-затрачено на выполнение задания. • Ответ 24 час.

• II способ (по свойству прямой пропорциональности) • 48: 16=3(раза)-в 3 раза больше нужно сделать деталей. • 8∙ 3=24 (час)-потребуется времени.

Задача на движение • 1. Белый медведь преодолевает расстояние, равное 100 дм. , за 5 сек. За какое время он преодолеет расстояние в 20 м. ? • 2. Пешеход, двигаясь со скоростью 6 верст в час, за некоторое время преодолевает расстояние, равное 24 верстам. С какой скоростью за тоже время он преодолеет расстояние, равное 36 верстам?

• Скорость галеры 10 узлов в час. На путь из Кронштадта в С-Петербург она затрачивает 4 час. Сколько часов затратит на этот путь фрегат, если его скорость в два раза больше скорость галеры?

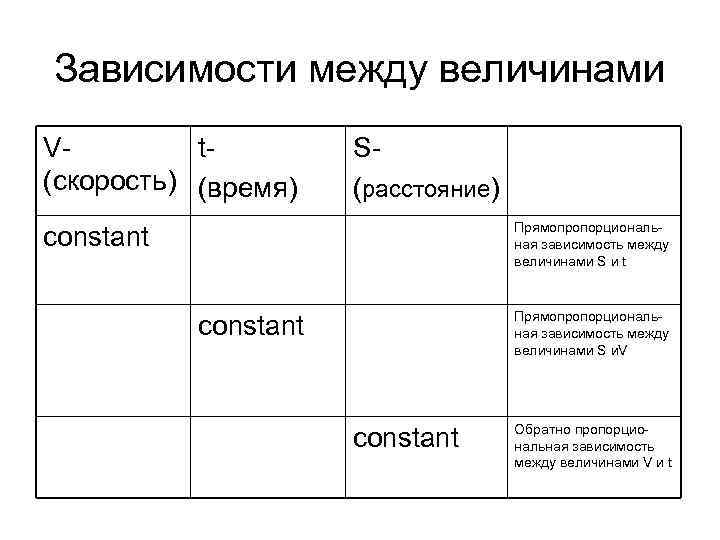
Зависимости между величинами Vt(скорость) (время) S(расстояние) Прямопропорциональная зависимость между величинами S и t constant Прямопропорциональная зависимость между величинами S и. V constant Обратно пропорциональная зависимость между величинами V и t

Зависимости между величинами V(скорость) t(время) S(расстояние) constant 5 сек ? 100 дм 2 м. Прямопропорциональная зависимость между величинами S иt 6 верст в час ? constant 24 версты 36 верст Прямопропорциональная зависимость между величинами S и. V constant Обратно пропорциональная зависимость между величинами V иt 10 узлов в час 4 час ?

СПАСИБО ЗА ВНИМАНИЕ!