элем_алг_логики.pptx
- Количество слайдов: 13

Элементы алгебры логики Алгебра логики Логическое высказывание (простое и составное) Джордж Буль (1815 -1864) Три – число четное (А=0) Три – число простое (В=1) Три – число нечетное и простое ( А В=1) Логическая операция (логическая связка)

• Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания. • Логическим высказыванием называют любое повествовательное предложение, в отношении которого однозначно известно, истинно оно или ложно. • Высказывания, образованные из других высказываний с помощью логических связок ( «и» , «или» , и др. ), называются сложными или составными. Высказывания, не являющиеся составными, называются элементарными. • Cложное высказывание, истинное для всех значений входящих в него переменных, называется тождественно истинным или тавтологией. Тавтологиями являются все математические законы, например: истинно для любых a и b следующее выражение: а 2 – в 2 = (а-в)(а+в). • Сложное высказывание, ложное при всех значениях входящих в него переменных, называется тождественно ложным. • Если значения сложных высказываний совпадают при всех возможных значениях входящих в них переменных, то такие высказывания называют равносильными, тождественными или 2 эквивалентными.

Логические операции • 1) Операция AND (И)- конъюнкция (лат. conjunctio – соединение), логическое умножение. Обозначается символом , иногда &. Она реализует следующую конструкцию логического высказывания: «результат операции будет истинным только в том случае, если оба входных сообщения истинны» : 1 1=1, 1 0=0, 0 1=0, 0 0=0. • 2) Операция OR (ИЛИ) – дизъюнкция (лат. disjunctio – разделение). Обозначается символом . Реализует словесную конструкцию: «результат будет истинным, если истинно хотя бы одно из входных сообщений» : 1 1=1, 1 0=1, 0 1=1, 0 0=0. • 3) Операция NOT (НЕ) – логическое отрицание. Обозначается символом Отличается от рассмотренных операций тем, что имеет только одно входное значение, причем результатом всегда будет значение противоположное, например: 3 ¬ 1=0, ¬ 0=1.

4) Операция XOR – исключающее ИЛИ. Обозначается символом . Реализует конструкцию «результат будет истинным, если истинно либо то, либо другое из входных значений, но не оба одновременно» , например: 1 1=0, 1 0=1, 0 1=1, 0 0=0. 5) Импликация (лат. implico – тесно связаны). Обозначается символом . Выражается в конструкциях: “если. . . , то”, “из. . . следует”, “. . . влечет. . . ”. Например, «из A следует B» , «если верно сообщение А, то верно и В» , «наступление события А влечет наступление события В» : A B. Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное (истинная предпосылка ведет к ложному выводу): 1 1=1, 1 0=0, 0 1=1, 0 0=1. 6) Эквиваленция (или двойная импликация). Обозначается символом или . Выражается высказываниями типа “тогда и только тогда”, "необходимо и достаточно”, “равносильно”. Например, «A равносильно B» (и наоборот)» , «для наступления события А необходимо и достаточно наступления события В» : A B. Эквивалентность двух высказываний истинна, тогда и только тогда, когда оба эти высказывания истинны, или оба ложны: 1 1=1, 1 0=0, 0 1=0, 0 0=1.

• Основными операциями считаются конъюнкция, дизъюнкция и отрицание. Через них можно выразить остальные. • Например, операция импликации выражается через отрицание и дизъюнкцию: A B = А В. • Операция эквивалентности заменяется двумя равносильными выражениями: A B = (A B) (¬A ¬B), A B = (A ¬B) (¬A B). • Порядок выполнения логических операций задается круглыми скобками. Иначе порядок действий следующий: сначала выполняется операция отрицания (NOT), затем конъюнкция (AND), после конъюнкции – дизъюнкция (OR или XOR) и в последнюю очередь – импликация и эквиваленция. • Пример сложного логического высказывания: А (B→C) D (A) Порядок выполнения: (А) – инверсия В → С – импликация (В → С) D – конъюнкция А (B → C) D – дизъюнкция А (B → C) D = не(A) – эквивалентность

Логические элементы цифровых автоматов Устройство, которое выдает результат булевой операции в компьютере (или в другом техническом устройстве), называется логическим элементом или вентилем. Физически вентиль – это небольшая электрическая цепь, в которой два значения 0 и 1 представляются разными уровнями электрического напряжения. Основные типы логических элементов x 1 x 2 & y=x 1 x 2 Схема И (конъюнкция) 0 0 1 1 x 2 0 1 y 0 0 0 1
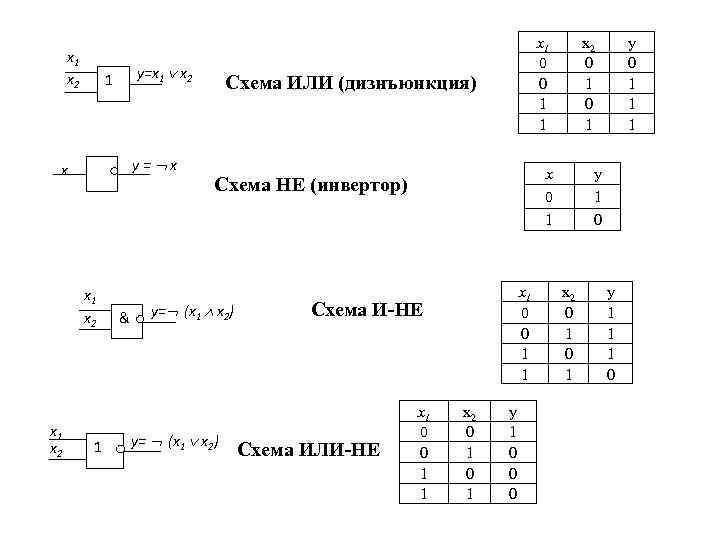
x 1 x 2 y=x 1 x 2 1 y= x x x 1 x 2 1 & x 1 0 0 1 1 Схема ИЛИ (дизнъюнкция) x 0 1 Схема НЕ (инвертор) y= (x 1 x 2) y= (x 1 x 2) x 1 0 0 1 1 Схема И-НЕ Схема ИЛИ-НЕ x 2 0 1 x 1 0 0 1 1 x 2 0 1 y 1 0 0 0 y 0 1 1 1 y 1 0 x 2 0 1 y 1 1 1 0
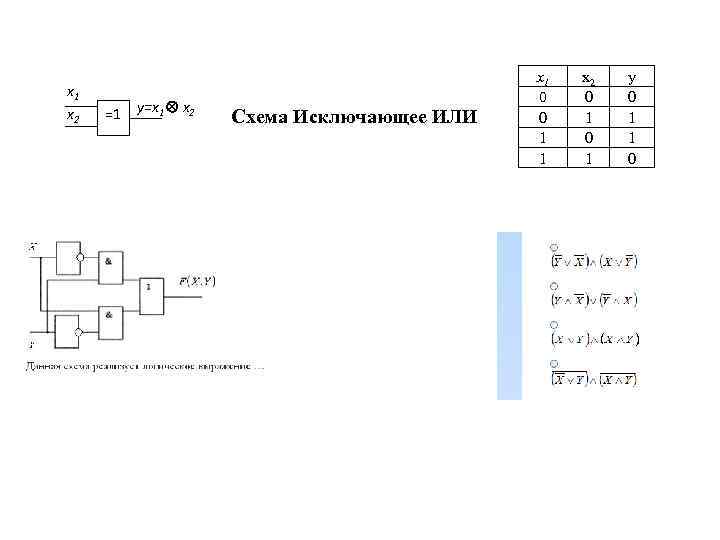
x 1 x 2 =1 y=x 1 x 2 Схема Исключающее ИЛИ x 1 0 0 1 1 x 2 0 1 y 0 1 1 0

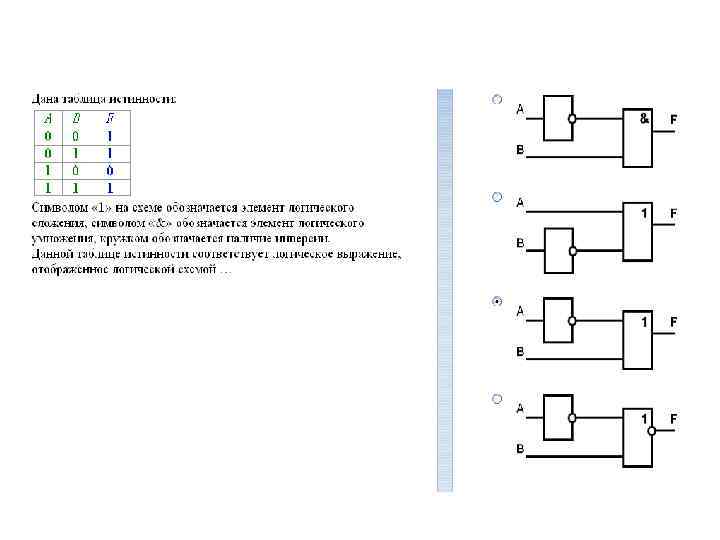



элем_алг_логики.pptx